2024-2025北师大八年级数学(下)第二章 一元一次不等式和一元一次不等式组 测试卷(含答案)
文档属性
| 名称 | 2024-2025北师大八年级数学(下)第二章 一元一次不等式和一元一次不等式组 测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 102.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-06 00:00:00 | ||
图片预览


文档简介
第二章一元一次不等式和一元一次不等式组测试卷
(时间:120分钟 满分:120分)
一、选择题(本大题共10 小题,每小题3分,共30分)
1.陈老师在黑板写了下列式子:①3>5;②1-x;③4x-5≠0;④2a≤6b;⑤x2+3x=10,其中不等式的个数有 ( )
A.1个 B.2个 C.3个 D.4个
2.若x>y,则下列式子错误的是 ( )
A. x-3>y-3 B.-3x>-3y C. x+3>y+3
3.不等式3x+2>-1的解集是 ( )
C. x>-1 D. x<-1
4.不等式-3x+6>0的正整数解有 ( )
A.1个 B.2个 C.3个 D.无数多个
5.如图,当y<0时,自变量x的范围是 ( )
A. x<-2 B. x>-2 C. x<2 D. x>2
6.不等式组--2≤x+1<1的解集在数轴上表示正确的是 ( )
7.观察函数y 和y 的图象,当x=1,两个函数值的大小为
( )
8.小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:至少15元.乙说:至多12元.丙说:至多10元.小明说:你们三个人都说错了.则这本书的价格x(元)所在的范围为 ( )
A.109.若关于x的一元一次不等式组 有解,则m的取值范围为 ( )
10.某单位向某村提供优质种羊若干只.在准备配发的过程中发现:公羊刚好每户1只;若每户发放母羊5 只,则多出17只母羊,若每户发放母羊7只,则有一户可分得母羊但不足3 只.这批种羊共 只. ( )
A.55 B.72 C.83 D.89
二、填空题(本大题共5 小题,每小题3分,共15分)
11.把“a的3倍与2的和不小于6”用不等式表示为 。
12.长度为3,7,x的三条线段可以围成一个三角形,则x的取值范围是 .
13.燃放某种礼花弹时,为了确保安全,人在点燃导火线后要在燃放前转移到 10m以外的安全区域,已知导火线的燃烧速度为0.2m/s,人离开的速度为4m/s,导火线的长度x(m)应满足的不等关系为 .
14.直线 与直线 在同一平面直角坐标系中的图象如图所示,则关于x的不等式 的解集为 .
15.已知点. 关于x轴的对称点 是第三象限内的整点(横、纵坐标都为整数的点,称为整点),则点 的坐标是 .
三、解答题(本大题共8小题,共75 分)
16.(8分)(1)解不等式:
(2)解不等式组:并在数轴上表示出不等式组的解集.
17.(9分)下面是小明解不等式 的过程:
解:去分母,得: …第一步
移项、合并同类项,得: …第二步
系数化为1,得:第三步.
(1)小明是从第 步开始出错的,错误的原因是 ;
(2)第三步“系数化为1”的依据是 ;
(3)请你给出正确的解答过程,并把此不等式的解集在数轴上表示出来.
18.(8分)学习中,小明发现:当n=1,2,3时, 的值都是负数.于是小明猜想:当n为任意正整数时, 的值都是负数.小明的猜想正确吗 请简要说明你的理由.
19.(9分)已知关于x、y的方程组 的解x为负数,y为非正数,求a的取值范围.
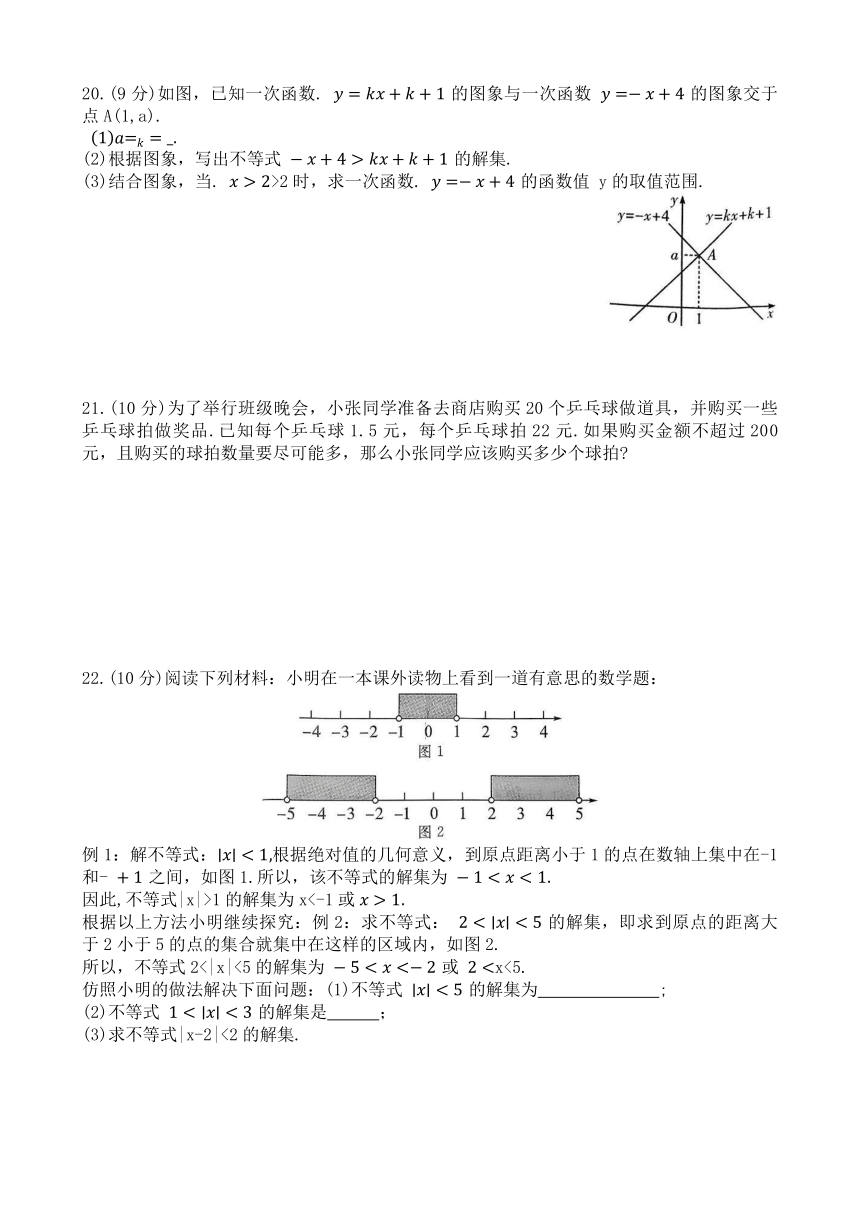
20.(9分)如图,已知一次函数. 的图象与一次函数 的图象交于点A(1,a).
(2)根据图象,写出不等式 的解集.
(3)结合图象,当. >2时,求一次函数. 的函数值 y的取值范围.
21.(10分)为了举行班级晚会,小张同学准备去商店购买20个乒乓球做道具,并购买一些乒乓球拍做奖品.已知每个乒乓球1.5元,每个乒乓球拍22元.如果购买金额不超过200元,且购买的球拍数量要尽可能多,那么小张同学应该购买多少个球拍
22.(10分)阅读下列材料:小明在一本课外读物上看到一道有意思的数学题:
例1:解不等式:根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和- 之间,如图1.所以,该不等式的解集为
因此,不等式|x|>1的解集为x<-1或
根据以上方法小明继续探究:例2:求不等式: 的解集,即求到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图2.
所以,不等式2<|x|<5的解集为 或 x<5.
仿照小明的做法解决下面问题:(1)不等式 的解集为 ;
(2)不等式 的解集是 ;
(3)求不等式|x-2|<2的解集.
23.(12分)书法是中华民族的文化瑰宝,是人类文明的宝贵财富,是我国基础教育的重要内容.某校准备在某超市为书法课购买一批毛笔和宣纸,已知毛笔的单价为5元,宣纸的单价为0.36元.该校准备购买毛笔50支,宣纸x张 ,该超市给出以下两种优惠方案.
方案 A:购买一支毛笔,赠送一张宣纸;
方案 B:购买的宣纸超出 200 张的部分打七五折,毛笔不打折.
设方案 A的总费用为y1元,方案B的总费用为y2元.
请分别求出y1,y2与x之间的函数表达式;
若该校准备购买的宣纸超过200张,则选择哪种方案更合算 请说明理由.
第二章测试卷答案
1. C 2. B 3. C 4. A 5. A 6. B 7. B 8. B 9. C 10. C
11.3a+2≥6 12.4 14. x<-1 15.(-1 1)
16.(1)x<-5.
(2)解①得x>3,
解②得x≥1, ∴不等式组的解集为x>3. 数轴表示略.
17.(1)一 -1漏乘了2
(2)不等式的基本性质
(3)正确的解答过如下:
x+5-2<3x+2, -2x<-1,
该不等式的解集在数轴上表示图略:
18.不正确.
解法一:(利用反例证明)例如:当n=7时, 解法二: ,当n≥6时,n -6n≥0.
19.解方程组得
由题意知
解不等式①,得:a<3,
解不等式②,得:a≥-2,
则不等式组的解集为-2≤a<3.
20.(1) 3 1
(2)根据图象可知,不等式-x+4> kx+k+1的解集为x<1;
(3)当x=2时,y=-x+4=-2+4=2,
∴x>2时,一次函数y=-x+4的函数值y的取值范围是y<2.
21.设小张同学应该购买x个球拍,依题意得1.5×20+22x≤200,解得: ∵x是整数, ∴x的最大值为7.
答:小张同学应该购买7个球拍.
22.(1)-5(2)-3(3)0
(时间:120分钟 满分:120分)
一、选择题(本大题共10 小题,每小题3分,共30分)
1.陈老师在黑板写了下列式子:①3>5;②1-x;③4x-5≠0;④2a≤6b;⑤x2+3x=10,其中不等式的个数有 ( )
A.1个 B.2个 C.3个 D.4个
2.若x>y,则下列式子错误的是 ( )
A. x-3>y-3 B.-3x>-3y C. x+3>y+3
3.不等式3x+2>-1的解集是 ( )
C. x>-1 D. x<-1
4.不等式-3x+6>0的正整数解有 ( )
A.1个 B.2个 C.3个 D.无数多个
5.如图,当y<0时,自变量x的范围是 ( )
A. x<-2 B. x>-2 C. x<2 D. x>2
6.不等式组--2≤x+1<1的解集在数轴上表示正确的是 ( )
7.观察函数y 和y 的图象,当x=1,两个函数值的大小为
( )
8.小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:至少15元.乙说:至多12元.丙说:至多10元.小明说:你们三个人都说错了.则这本书的价格x(元)所在的范围为 ( )
A.10
10.某单位向某村提供优质种羊若干只.在准备配发的过程中发现:公羊刚好每户1只;若每户发放母羊5 只,则多出17只母羊,若每户发放母羊7只,则有一户可分得母羊但不足3 只.这批种羊共 只. ( )
A.55 B.72 C.83 D.89
二、填空题(本大题共5 小题,每小题3分,共15分)
11.把“a的3倍与2的和不小于6”用不等式表示为 。
12.长度为3,7,x的三条线段可以围成一个三角形,则x的取值范围是 .
13.燃放某种礼花弹时,为了确保安全,人在点燃导火线后要在燃放前转移到 10m以外的安全区域,已知导火线的燃烧速度为0.2m/s,人离开的速度为4m/s,导火线的长度x(m)应满足的不等关系为 .
14.直线 与直线 在同一平面直角坐标系中的图象如图所示,则关于x的不等式 的解集为 .
15.已知点. 关于x轴的对称点 是第三象限内的整点(横、纵坐标都为整数的点,称为整点),则点 的坐标是 .
三、解答题(本大题共8小题,共75 分)
16.(8分)(1)解不等式:
(2)解不等式组:并在数轴上表示出不等式组的解集.
17.(9分)下面是小明解不等式 的过程:
解:去分母,得: …第一步
移项、合并同类项,得: …第二步
系数化为1,得:第三步.
(1)小明是从第 步开始出错的,错误的原因是 ;
(2)第三步“系数化为1”的依据是 ;
(3)请你给出正确的解答过程,并把此不等式的解集在数轴上表示出来.
18.(8分)学习中,小明发现:当n=1,2,3时, 的值都是负数.于是小明猜想:当n为任意正整数时, 的值都是负数.小明的猜想正确吗 请简要说明你的理由.
19.(9分)已知关于x、y的方程组 的解x为负数,y为非正数,求a的取值范围.
20.(9分)如图,已知一次函数. 的图象与一次函数 的图象交于点A(1,a).
(2)根据图象,写出不等式 的解集.
(3)结合图象,当. >2时,求一次函数. 的函数值 y的取值范围.
21.(10分)为了举行班级晚会,小张同学准备去商店购买20个乒乓球做道具,并购买一些乒乓球拍做奖品.已知每个乒乓球1.5元,每个乒乓球拍22元.如果购买金额不超过200元,且购买的球拍数量要尽可能多,那么小张同学应该购买多少个球拍
22.(10分)阅读下列材料:小明在一本课外读物上看到一道有意思的数学题:
例1:解不等式:根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和- 之间,如图1.所以,该不等式的解集为
因此,不等式|x|>1的解集为x<-1或
根据以上方法小明继续探究:例2:求不等式: 的解集,即求到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图2.
所以,不等式2<|x|<5的解集为 或 x<5.
仿照小明的做法解决下面问题:(1)不等式 的解集为 ;
(2)不等式 的解集是 ;
(3)求不等式|x-2|<2的解集.
23.(12分)书法是中华民族的文化瑰宝,是人类文明的宝贵财富,是我国基础教育的重要内容.某校准备在某超市为书法课购买一批毛笔和宣纸,已知毛笔的单价为5元,宣纸的单价为0.36元.该校准备购买毛笔50支,宣纸x张 ,该超市给出以下两种优惠方案.
方案 A:购买一支毛笔,赠送一张宣纸;
方案 B:购买的宣纸超出 200 张的部分打七五折,毛笔不打折.
设方案 A的总费用为y1元,方案B的总费用为y2元.
请分别求出y1,y2与x之间的函数表达式;
若该校准备购买的宣纸超过200张,则选择哪种方案更合算 请说明理由.
第二章测试卷答案
1. C 2. B 3. C 4. A 5. A 6. B 7. B 8. B 9. C 10. C
11.3a+2≥6 12.4
16.(1)x<-5.
(2)解①得x>3,
解②得x≥1, ∴不等式组的解集为x>3. 数轴表示略.
17.(1)一 -1漏乘了2
(2)不等式的基本性质
(3)正确的解答过如下:
x+5-2<3x+2, -2x<-1,
该不等式的解集在数轴上表示图略:
18.不正确.
解法一:(利用反例证明)例如:当n=7时, 解法二: ,当n≥6时,n -6n≥0.
19.解方程组得
由题意知
解不等式①,得:a<3,
解不等式②,得:a≥-2,
则不等式组的解集为-2≤a<3.
20.(1) 3 1
(2)根据图象可知,不等式-x+4> kx+k+1的解集为x<1;
(3)当x=2时,y=-x+4=-2+4=2,
∴x>2时,一次函数y=-x+4的函数值y的取值范围是y<2.
21.设小张同学应该购买x个球拍,依题意得1.5×20+22x≤200,解得: ∵x是整数, ∴x的最大值为7.
答:小张同学应该购买7个球拍.
22.(1)-5
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
