3.3垂径定理培优练习(无答案)北师大版2024—2025学年九年级下册
文档属性
| 名称 | 3.3垂径定理培优练习(无答案)北师大版2024—2025学年九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 329.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 22:37:03 | ||
图片预览



文档简介
3.3垂径定理培优练习北师大版2024—2025学年九年级下册
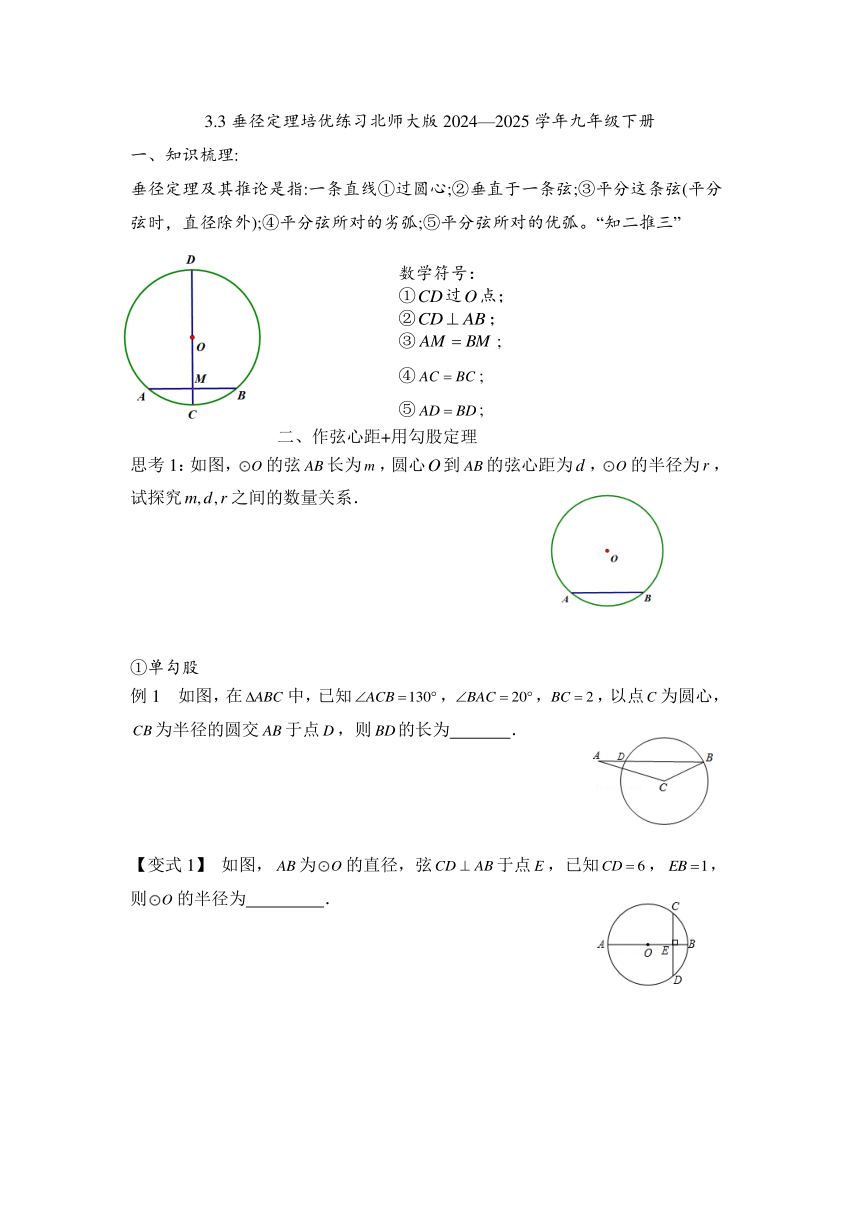
一、知识梳理:
垂径定理及其推论是指:一条直线①过圆心;②垂直于一条弦;③平分这条弦(平分弦时,直径除外);④平分弦所对的劣弧;⑤平分弦所对的优弧。“知二推三”
数学符号:
①过点;
②;
③;
④;
⑤;
二、作弦心距+用勾股定理
思考1:如图,的弦长为,圆心到的弦心距为,的半径为,试探究之间的数量关系.
①单勾股
例1 如图,在中,已知,,,以点为圆心,为半径的圆交于点,则的长为 .
【变式1】 如图,为的直径,弦于点,已知,,则的半径为 .
②双勾股
例2 如图,已知半径为2的有两条互相垂直的弦和,其交点到圆心的距离为1,则 .
【变式2】如图,,,,是半径为1的上按逆时针方向排列的四个动点,,当时,求的取值范围;
三、弧中点→连半径,得垂径
思考2: 如图,是的弦,是的中点,你能得到那些结论
例3 如图,为直径,为弧的中点,于,
(1)求证:为的切线;
(2)已知:,,求的半径.
【变式3】如图,已知是的直径,与的两直角边分别交于点、,点是弧的中点,,连接.
(1)求证:直线是的切线.
(2)若,,求的值.
四、课后练习:
(一)、选择题
1.下列命题中错误的有( ).
(1)弦的垂直平分线经过圆心;(2)平分弦的直径垂直于弦;
(3)所夹弧相等的两条弦平行;(4)圆的对称轴是直径.
A.1个 B.2个 C.3个 D.4个
2.如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
A.CE=DE B.AE=OE C.= D. △OCE≌△ODE
第2题图 第3题图 第4题图
3.如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=,BD=,则AB的长为( )
A.2 B.3 C.4 D.5
4.如图所示,矩形ABCD与⊙O相交于M、N、F、E,若AM=2,DE=1,EF=8,则MN的长为( )
A.2 B.4 C.6 D.8
5.已知⊙O的直径AB=12cm,P为OB中点,过P作弦CD与AB相交成30°角,则弦CD的长为( ).
A.cm B.cm C.cm D.cm
二、填空题
6.如图,CD为⊙O的直径,AB⊥CD于E,DE=8cm,CE=2cm,则AB=______cm.
第6题图 第7题图 第8题图
7.如图,⊙O的半径OC为6cm,弦AB垂直平分OC,则AB=______cm,∠AOB=______°.
8.如图,AB是⊙O的直径,CD为⊙O的一条弦,CD⊥AB于E,CD=4,AE=1,则⊙O的半径为 .
9.如图,⊙O的弦AB垂直于CD,E为垂足,AE=3,BE=7,则圆心O到CD的距离是______.
第9题图 第10题图
10.如图,P为⊙O的弦AB上的点,PA=6,PB=2,⊙O的半径为5,则OP=______.
11.如图,点A、B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合)连结AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF= .
第11题图 第12题图
如图,AB是⊙O的直径,弦CD⊥AB于E,连接AC.若∠CAB=22.5°,
CD=8cm,则⊙O的半径为 cm.
三、解答题
13.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=8,求CD的长.
14.如图,⊙O的两条弦AB、CD交于点E,OE平分∠BED.
(1)求证:AB=CD;
(2)若∠BED=60°,EO=2,求DE﹣AE的值.
15.如图所示,已知O是∠MPN的平分线上的一点,以O为圆心的圆与角的两边分别交于点A、B和C、D.
⑴求证:PB=PD.
⑵若角的顶点P在圆上或圆内,⑴中的结论还成立吗?若不成立,请说明理由;若成立,请加以证明.
16.如图,点为 弧的中点,点为上一点,,,求的半径长.
17.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线交AB的延长线于点G,垂足为点F,连接AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求弦DB的长度.
一、知识梳理:
垂径定理及其推论是指:一条直线①过圆心;②垂直于一条弦;③平分这条弦(平分弦时,直径除外);④平分弦所对的劣弧;⑤平分弦所对的优弧。“知二推三”
数学符号:
①过点;
②;
③;
④;
⑤;
二、作弦心距+用勾股定理
思考1:如图,的弦长为,圆心到的弦心距为,的半径为,试探究之间的数量关系.
①单勾股
例1 如图,在中,已知,,,以点为圆心,为半径的圆交于点,则的长为 .
【变式1】 如图,为的直径,弦于点,已知,,则的半径为 .
②双勾股
例2 如图,已知半径为2的有两条互相垂直的弦和,其交点到圆心的距离为1,则 .
【变式2】如图,,,,是半径为1的上按逆时针方向排列的四个动点,,当时,求的取值范围;
三、弧中点→连半径,得垂径
思考2: 如图,是的弦,是的中点,你能得到那些结论
例3 如图,为直径,为弧的中点,于,
(1)求证:为的切线;
(2)已知:,,求的半径.
【变式3】如图,已知是的直径,与的两直角边分别交于点、,点是弧的中点,,连接.
(1)求证:直线是的切线.
(2)若,,求的值.
四、课后练习:
(一)、选择题
1.下列命题中错误的有( ).
(1)弦的垂直平分线经过圆心;(2)平分弦的直径垂直于弦;
(3)所夹弧相等的两条弦平行;(4)圆的对称轴是直径.
A.1个 B.2个 C.3个 D.4个
2.如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
A.CE=DE B.AE=OE C.= D. △OCE≌△ODE
第2题图 第3题图 第4题图
3.如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=,BD=,则AB的长为( )
A.2 B.3 C.4 D.5
4.如图所示,矩形ABCD与⊙O相交于M、N、F、E,若AM=2,DE=1,EF=8,则MN的长为( )
A.2 B.4 C.6 D.8
5.已知⊙O的直径AB=12cm,P为OB中点,过P作弦CD与AB相交成30°角,则弦CD的长为( ).
A.cm B.cm C.cm D.cm
二、填空题
6.如图,CD为⊙O的直径,AB⊥CD于E,DE=8cm,CE=2cm,则AB=______cm.
第6题图 第7题图 第8题图
7.如图,⊙O的半径OC为6cm,弦AB垂直平分OC,则AB=______cm,∠AOB=______°.
8.如图,AB是⊙O的直径,CD为⊙O的一条弦,CD⊥AB于E,CD=4,AE=1,则⊙O的半径为 .
9.如图,⊙O的弦AB垂直于CD,E为垂足,AE=3,BE=7,则圆心O到CD的距离是______.
第9题图 第10题图
10.如图,P为⊙O的弦AB上的点,PA=6,PB=2,⊙O的半径为5,则OP=______.
11.如图,点A、B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合)连结AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF= .
第11题图 第12题图
如图,AB是⊙O的直径,弦CD⊥AB于E,连接AC.若∠CAB=22.5°,
CD=8cm,则⊙O的半径为 cm.
三、解答题
13.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=8,求CD的长.
14.如图,⊙O的两条弦AB、CD交于点E,OE平分∠BED.
(1)求证:AB=CD;
(2)若∠BED=60°,EO=2,求DE﹣AE的值.
15.如图所示,已知O是∠MPN的平分线上的一点,以O为圆心的圆与角的两边分别交于点A、B和C、D.
⑴求证:PB=PD.
⑵若角的顶点P在圆上或圆内,⑴中的结论还成立吗?若不成立,请说明理由;若成立,请加以证明.
16.如图,点为 弧的中点,点为上一点,,,求的半径长.
17.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线交AB的延长线于点G,垂足为点F,连接AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求弦DB的长度.
