3.7切线长定理知识梳理与培优练习(无答案)北师大2024—2025学年九年级下册
文档属性
| 名称 | 3.7切线长定理知识梳理与培优练习(无答案)北师大2024—2025学年九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 68.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 00:00:00 | ||
图片预览


文档简介
3.7切线长定理知识梳理与培优练习北师大2024—2025学年九年级下册
【知识梳理】
切线长定理:从圆外一点可以引圆的两条切线,它们的_________相等,这一点和圆心的连线平分__________________.
1.证明切线长定理
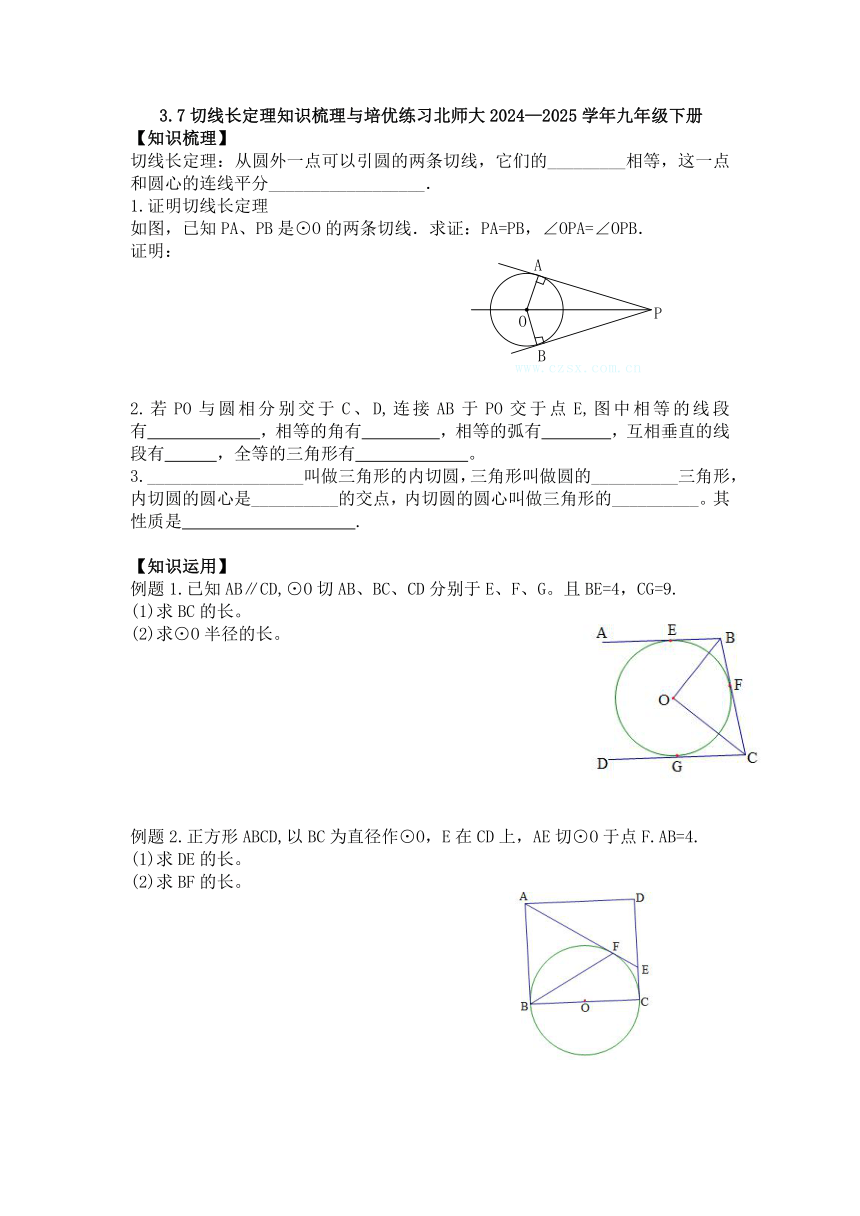
如图,已知PA、PB是⊙O的两条切线.求证:PA=PB,∠OPA=∠OPB.
证明:
2.若PO与圆相分别交于C、D,连接AB于PO交于点E,图中相等的线段有 ,相等的角有 ,相等的弧有 ,互相垂直的线段有 ,全等的三角形有 。
3.__________________叫做三角形的内切圆,三角形叫做圆的__________三角形,内切圆的圆心是__________的交点,内切圆的圆心叫做三角形的__________。其性质是 .
【知识运用】
例题1.已知AB∥CD,⊙O切AB、BC、CD分别于E、F、G。且BE=4,CG=9.
求BC的长。
求⊙O半径的长。
例题2.正方形ABCD,以BC为直径作⊙O,E在CD上,AE切⊙O于点F.AB=4.
求DE的长。
求BF的长。
例题3.如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长。
内切圆半径的求法与内心的性质运用
例题4.已知,如图,⊙O是Rt△ABC的内切圆,∠C=90°若AC=12cm,BC=9cm,求⊙O的半径r;
例题5.如图,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AE=1,CD=2,BF=3,且△ABC的面积为6.求内切圆的半径r.
例题6.△ABC中,I为内心,O为外心,AI的延长线交⊙O于E.证明;EI=EC.
例题7.AB为⊙O的直径,PB、PD为⊙O的切线,B、D为切点,PO交⊙O于E,交BD于F.证明:E为△PBD的内心。
巩固练习
1.如图,PA,PB分别为⊙O的切线,AC为直径,切点分别为A、B,∠P=70°,则∠C=
2.已知:如图5,⊙O是△ABC的内切圆,切点
分别为D、E、F,(1)图中共有 对相等线段?
(2)若AD=4,BC=5,CF=6,则△ABC的周长是__;
(3)若AB=4,BC=5,AC=6,则AD=__,BE=__,CF=__.
3.在⊿ABC中,∠A=50°
(1)若点O是⊿ABC的外心,则∠BOC= .
(2) 若点O是⊿ABC的内心,则∠BOC= .
4.如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=30°.
(1)求∠APB的度数; (2)当OA=3时,求AP的长.
5.如图,PA、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切
线,切点为Q,交PA、PB为E、F点,已知,求△PEF的周长.
6.如图,边长为6的正三角形的内切圆半径是_________.
7.如图,圆O内切Rt△ABC,切点分别是D、E、F,AC=5,BC=12,则内切圆的半径长为
8.如图所示,EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点, 如果∠E=46°,∠DCF=32°,求∠A的度数.
【知识梳理】
切线长定理:从圆外一点可以引圆的两条切线,它们的_________相等,这一点和圆心的连线平分__________________.
1.证明切线长定理
如图,已知PA、PB是⊙O的两条切线.求证:PA=PB,∠OPA=∠OPB.
证明:
2.若PO与圆相分别交于C、D,连接AB于PO交于点E,图中相等的线段有 ,相等的角有 ,相等的弧有 ,互相垂直的线段有 ,全等的三角形有 。
3.__________________叫做三角形的内切圆,三角形叫做圆的__________三角形,内切圆的圆心是__________的交点,内切圆的圆心叫做三角形的__________。其性质是 .
【知识运用】
例题1.已知AB∥CD,⊙O切AB、BC、CD分别于E、F、G。且BE=4,CG=9.
求BC的长。
求⊙O半径的长。
例题2.正方形ABCD,以BC为直径作⊙O,E在CD上,AE切⊙O于点F.AB=4.
求DE的长。
求BF的长。
例题3.如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长。
内切圆半径的求法与内心的性质运用
例题4.已知,如图,⊙O是Rt△ABC的内切圆,∠C=90°若AC=12cm,BC=9cm,求⊙O的半径r;
例题5.如图,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AE=1,CD=2,BF=3,且△ABC的面积为6.求内切圆的半径r.
例题6.△ABC中,I为内心,O为外心,AI的延长线交⊙O于E.证明;EI=EC.
例题7.AB为⊙O的直径,PB、PD为⊙O的切线,B、D为切点,PO交⊙O于E,交BD于F.证明:E为△PBD的内心。
巩固练习
1.如图,PA,PB分别为⊙O的切线,AC为直径,切点分别为A、B,∠P=70°,则∠C=
2.已知:如图5,⊙O是△ABC的内切圆,切点
分别为D、E、F,(1)图中共有 对相等线段?
(2)若AD=4,BC=5,CF=6,则△ABC的周长是__;
(3)若AB=4,BC=5,AC=6,则AD=__,BE=__,CF=__.
3.在⊿ABC中,∠A=50°
(1)若点O是⊿ABC的外心,则∠BOC= .
(2) 若点O是⊿ABC的内心,则∠BOC= .
4.如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=30°.
(1)求∠APB的度数; (2)当OA=3时,求AP的长.
5.如图,PA、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切
线,切点为Q,交PA、PB为E、F点,已知,求△PEF的周长.
6.如图,边长为6的正三角形的内切圆半径是_________.
7.如图,圆O内切Rt△ABC,切点分别是D、E、F,AC=5,BC=12,则内切圆的半径长为
8.如图所示,EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点, 如果∠E=46°,∠DCF=32°,求∠A的度数.
