2.1.1 平方根与算术平方根 课件(共25张PPT)
文档属性
| 名称 | 2.1.1 平方根与算术平方根 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 635.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-06 06:25:35 | ||
图片预览








文档简介
(共25张PPT)
平方根与算术平方根
七年级下册 第二章 2.1.1
学习目标
1.理解平方根与算术平方根的概念,明确两者的区别与联系。
2.掌握算术平方根的符号表示()及非负性(a≥0,≥0)。
3.能正确求出一个非负数的算术平方根及平方根,并解决简单实际问题。
4.经历从具体实例(如正方形面积)到抽象概念的归纳过程,培养观察与概括能力。
问题导入
小明将一个长为2、宽为1的长方形纸片,按图所示方法剪拼成了一个正方形 . 观察图中过程,由此你能发现这个正方形的面积是多少吗?它的边长呢?
说一说
沿虚线对折
问题导入
再沿虚线对折
展开铺平
剪开铺平
问题导入
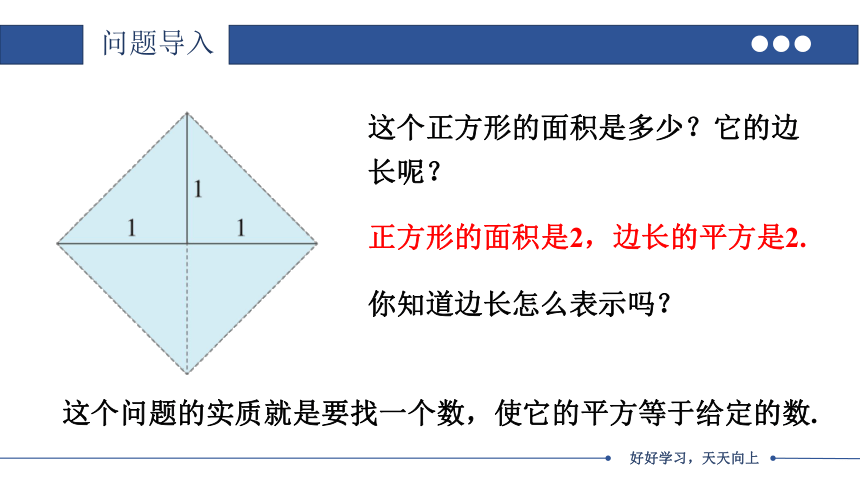
这个正方形的面积是多少?它的边长呢?
正方形的面积是2,边长的平方是2.
你知道边长怎么表示吗?
这个问题的实质就是要找一个数,使它的平方等于给定的数.
新知探究
抽象
如果有一个数r,使得r2=a,那么r叫作a的一个平方根,也叫作二次方根.
若r2=a,则r是a的一个平方根.
例如,由于22=4,因此2是4的一个平方根.
又因为(-2)2=4,所以-2也是4的一个平方根.
4的平方根除了2和-2以外,还有其他的数吗?
新知探究
探究
∵边长大于2的正方形的面积一定大于4,
∴比2大的数都不是4的平方根.
∵边长小于2的正方形的面积一定小于4,
∴比2小的正数都不是4的平方根.
4的平方根除了2和-2以外,还有其他的数吗?
新知探究
探究
又∵(-b)2=b2
∴大于-2或小于-2的负数都不是4的平方根.
又∵0显然不是4的平方根.
∴4的平方根有且只有两个:2与-2.
新知探究
定义
如果r是正数a的一个平方根,那么a的平方根有且只有两个:r与-r.
正数a的正平方根叫作a的算术平方根,记作,读作“根号a”;
正数a的负平方根记作,读作“负根号a”.
这样,正数a的两个平方根可以用“±”来表示,读作“正、负根号a”.
新知探究
注意:1.一个正数有两个平方根,且它们互为相反数 . 一个正数只有一个算术平方根.
2.算术平方根具有双重非负性:
①根号内的数a是非负数,即a≥0.
②算术平方根是非负数,即 ≥0.
0的平方根是多少?负数有平方根吗?
新知探究
思考
∵02= 0,
又∵非零数的平方不等于0,
∴0的平方根就是0本身.
∵同号两数相乘得正数,且02= 0,
∴不存在一个数的平方是负数,
∴负数没有平方根.
0的平方根也叫作0的算术平方根,记作0,即02=0.
判断下列语句是否正确:
3是9的平方根;
9的平方根是3;
4是-16的平方根;
0的平方根是0;
算术平方根等于本身的数只有0.
新知探究
牛刀小试
√
×
×
√
×
新知探究
注意
0的平方根就是0本身。
负数没有平方根。
算术平方根等于本身的数只有0和1。
新知探究
求一个非负数的平方根的运算,叫作开平方. 这个非负数叫作被开方数.
a
开平方
平方
开平方与平方互为逆运算.
例1 分别求下列各数的平方根:(1)36; (2) ; (3)1.21.
例题探究
解:(1)由于(±6)2=36,因此36的平方根是6与-6,即
.
(2)由于(±)2=,因此的平方根是与,即
.
(3)由于(±1.1)2=1.21,因此1.21的平方根是1.1与-1.1,即
.
例2分别求下列各数的算术平方根:
(1)100; (2)1.96; (3).
例题探究
解: (1)由于102=100,因此=10;
(2)由于1.42=1.96,因此=1.4;
(3)由于2= ,因此= ;
正数越大,它的算术平方根也越大。
新知探究
议一议
下列各数有平方根吗?如有,分别是多少?
(1) ; (2) (-5)2.
解:(1)∵=81,(±9)2=81,
∴的平方根是9与-9,即
(2)∵(-5)2=25,(±5)2=25,
∴(-5)2的平方根是5与-5,即
课堂练习
1. 25的平方根是 ( )
A.25 B.-5 C.5 D.±5
2. (-2)2的平方根是 ( )
A.2 B.-2 C.±2 D.
3.化简的结果是 ( )
A. 9 B. -3 C. ±3 D. 3
D
C
D
课堂练习
4.下列说法正确的有 ( )
①-2是-4的一个平方根;②a2的平方根是a;③2是4的一个平方根;④4的平方根是-2.
A. 1个
B. 2个
C. 3个
D. 4个
A
课堂练习
5.若13是m的一个平方根, 则m的另一个平方根是 ( )
A. 13
B. -13
C. ±13
D. 69
B
课堂练习
6.求下列各数的平方根:
(1)121. (2)0.01. (3)2. (4)(-13)2.
解:(1)由于(±11)2=121,因此121的平方根是11与-11.
(2)由于(±0.1)2=0.01,因此0.01的平方根是0.1与-0.1.
(3)2=,由于=,因此2的平方根是与- .
(4)(-13)2=169,由于(±13)2=169,因此(-13)2的平方根是13与-13.
课堂练习
7.一个正数b的两个不同的平方根分别是2a-1与-a+2,求a和b的值.
解:∵正数b的两个不同的平方根分别是2a-1与-a+2,
∴-a+2+2a-1=0,
∴a=-1,
∴-a+2=-(-1)+2=3,2a-1=2×(-1)-1=-3,
∵9的平方根是±3,
∴b=9.
课堂小结
1.一个正数有两个平方根,且它们互为相反数 . 一个正数只有一个算术平方根.
2.算术平方根具有双重非负性:
①根号内的数a是非负数,即a≥0.
②算术平方根是非负数,即 ≥0.
3.0的平方根就是0本身。
4.负数没有平方根。
5.算术平方根等于本身的数只有0和1。
课后作业
课堂作业:P31 T1-3
家庭作业:《学法》P24 A组(必做)
B组(选做)
平方根与算术平方根
七年级下册 第二章 2.1.1
学习目标
1.理解平方根与算术平方根的概念,明确两者的区别与联系。
2.掌握算术平方根的符号表示()及非负性(a≥0,≥0)。
3.能正确求出一个非负数的算术平方根及平方根,并解决简单实际问题。
4.经历从具体实例(如正方形面积)到抽象概念的归纳过程,培养观察与概括能力。
问题导入
小明将一个长为2、宽为1的长方形纸片,按图所示方法剪拼成了一个正方形 . 观察图中过程,由此你能发现这个正方形的面积是多少吗?它的边长呢?
说一说
沿虚线对折
问题导入
再沿虚线对折
展开铺平
剪开铺平
问题导入
这个正方形的面积是多少?它的边长呢?
正方形的面积是2,边长的平方是2.
你知道边长怎么表示吗?
这个问题的实质就是要找一个数,使它的平方等于给定的数.
新知探究
抽象
如果有一个数r,使得r2=a,那么r叫作a的一个平方根,也叫作二次方根.
若r2=a,则r是a的一个平方根.
例如,由于22=4,因此2是4的一个平方根.
又因为(-2)2=4,所以-2也是4的一个平方根.
4的平方根除了2和-2以外,还有其他的数吗?
新知探究
探究
∵边长大于2的正方形的面积一定大于4,
∴比2大的数都不是4的平方根.
∵边长小于2的正方形的面积一定小于4,
∴比2小的正数都不是4的平方根.
4的平方根除了2和-2以外,还有其他的数吗?
新知探究
探究
又∵(-b)2=b2
∴大于-2或小于-2的负数都不是4的平方根.
又∵0显然不是4的平方根.
∴4的平方根有且只有两个:2与-2.
新知探究
定义
如果r是正数a的一个平方根,那么a的平方根有且只有两个:r与-r.
正数a的正平方根叫作a的算术平方根,记作,读作“根号a”;
正数a的负平方根记作,读作“负根号a”.
这样,正数a的两个平方根可以用“±”来表示,读作“正、负根号a”.
新知探究
注意:1.一个正数有两个平方根,且它们互为相反数 . 一个正数只有一个算术平方根.
2.算术平方根具有双重非负性:
①根号内的数a是非负数,即a≥0.
②算术平方根是非负数,即 ≥0.
0的平方根是多少?负数有平方根吗?
新知探究
思考
∵02= 0,
又∵非零数的平方不等于0,
∴0的平方根就是0本身.
∵同号两数相乘得正数,且02= 0,
∴不存在一个数的平方是负数,
∴负数没有平方根.
0的平方根也叫作0的算术平方根,记作0,即02=0.
判断下列语句是否正确:
3是9的平方根;
9的平方根是3;
4是-16的平方根;
0的平方根是0;
算术平方根等于本身的数只有0.
新知探究
牛刀小试
√
×
×
√
×
新知探究
注意
0的平方根就是0本身。
负数没有平方根。
算术平方根等于本身的数只有0和1。
新知探究
求一个非负数的平方根的运算,叫作开平方. 这个非负数叫作被开方数.
a
开平方
平方
开平方与平方互为逆运算.
例1 分别求下列各数的平方根:(1)36; (2) ; (3)1.21.
例题探究
解:(1)由于(±6)2=36,因此36的平方根是6与-6,即
.
(2)由于(±)2=,因此的平方根是与,即
.
(3)由于(±1.1)2=1.21,因此1.21的平方根是1.1与-1.1,即
.
例2分别求下列各数的算术平方根:
(1)100; (2)1.96; (3).
例题探究
解: (1)由于102=100,因此=10;
(2)由于1.42=1.96,因此=1.4;
(3)由于2= ,因此= ;
正数越大,它的算术平方根也越大。
新知探究
议一议
下列各数有平方根吗?如有,分别是多少?
(1) ; (2) (-5)2.
解:(1)∵=81,(±9)2=81,
∴的平方根是9与-9,即
(2)∵(-5)2=25,(±5)2=25,
∴(-5)2的平方根是5与-5,即
课堂练习
1. 25的平方根是 ( )
A.25 B.-5 C.5 D.±5
2. (-2)2的平方根是 ( )
A.2 B.-2 C.±2 D.
3.化简的结果是 ( )
A. 9 B. -3 C. ±3 D. 3
D
C
D
课堂练习
4.下列说法正确的有 ( )
①-2是-4的一个平方根;②a2的平方根是a;③2是4的一个平方根;④4的平方根是-2.
A. 1个
B. 2个
C. 3个
D. 4个
A
课堂练习
5.若13是m的一个平方根, 则m的另一个平方根是 ( )
A. 13
B. -13
C. ±13
D. 69
B
课堂练习
6.求下列各数的平方根:
(1)121. (2)0.01. (3)2. (4)(-13)2.
解:(1)由于(±11)2=121,因此121的平方根是11与-11.
(2)由于(±0.1)2=0.01,因此0.01的平方根是0.1与-0.1.
(3)2=,由于=,因此2的平方根是与- .
(4)(-13)2=169,由于(±13)2=169,因此(-13)2的平方根是13与-13.
课堂练习
7.一个正数b的两个不同的平方根分别是2a-1与-a+2,求a和b的值.
解:∵正数b的两个不同的平方根分别是2a-1与-a+2,
∴-a+2+2a-1=0,
∴a=-1,
∴-a+2=-(-1)+2=3,2a-1=2×(-1)-1=-3,
∵9的平方根是±3,
∴b=9.
课堂小结
1.一个正数有两个平方根,且它们互为相反数 . 一个正数只有一个算术平方根.
2.算术平方根具有双重非负性:
①根号内的数a是非负数,即a≥0.
②算术平方根是非负数,即 ≥0.
3.0的平方根就是0本身。
4.负数没有平方根。
5.算术平方根等于本身的数只有0和1。
课后作业
课堂作业:P31 T1-3
家庭作业:《学法》P24 A组(必做)
B组(选做)
同课章节目录
