1.1.1 同底数幂的乘法(共16张PPT)2024~2025学年湘教版初中数学七年级下册
文档属性
| 名称 | 1.1.1 同底数幂的乘法(共16张PPT)2024~2025学年湘教版初中数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 21:46:11 | ||
图片预览





文档简介
(共16张PPT)
第1章 整式的乘法
1.1.1 同底数幂的乘法
1.理解同底数幂的乘法法则.
2.能够运用同底数幂的乘法法则进行相关计算.
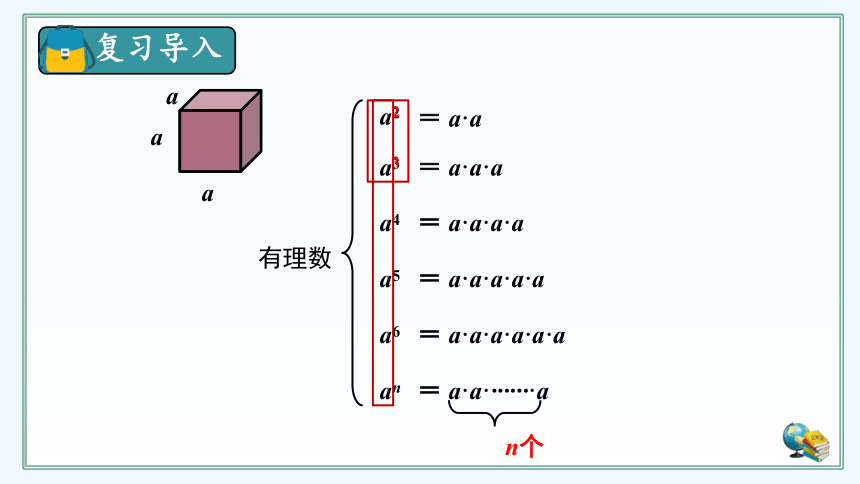
a
a
a2
a
a3
= a·a
= a·a·a
2
3
a4
a5
a6
an
= a·a·a·a
= a·a·a·a·a
= a·a·a·a·a·a
= a·a········a
n个
有理数
n
a
an
= a·a········a
n个
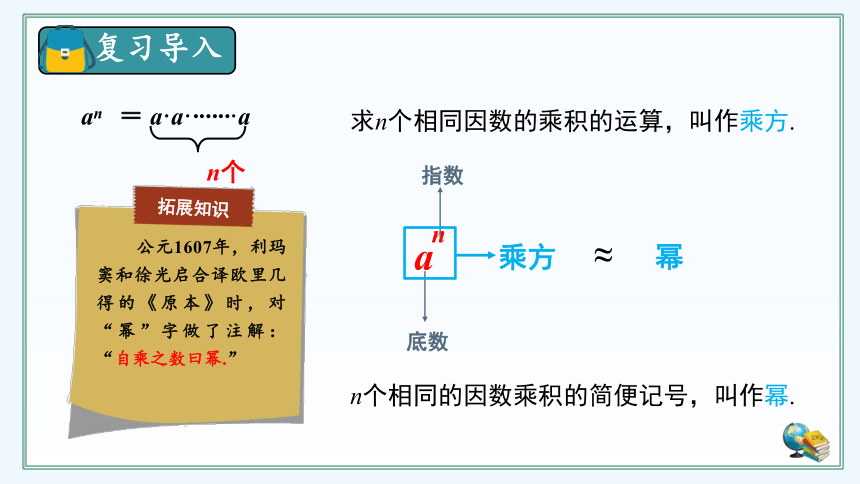
求n个相同因数的乘积的运算,叫作乘方.
底数
指数
乘方
幂
≈
n个相同的因数乘积的简便记号,叫作幂.
公元1607年,利玛窦和徐光启合译欧里几得的《原本》时,对“幂”字做了注解:“自乘之数曰幂.”
拓展知识
22×24= ; a2·a4= ;
a3·am= ;(m是正整数)
×
×
比较上述等式两端的底数和指数,你会发现什么?
说一说
底数不变,指数相加.
一般地,若m,n都是正整数,则
也就是
即:同底数幂相乘,底数不变,指数相加.
例 1
计算:
(1)105×103;
(2)x3 · x4.
解: 105×103
= 105+3
= 108.
解: x3 · x4
= x3+4
= x7.
[教材P3 例题1]
下列计算对不对?如果不对,应该怎样改正?
(1) a2 · a5= a10.
(2) a3 · a3= 2a6.
(3) a · a4= a4.
(1) a2 · a5= a7.
(2) a3 · a3= a6.
(3) a · a4= a5.
×
×
×
(1) -a·a3;
解: -a·a3
= (-1)·a1+3
=﹣a4
(2) -y n · y n+1 (n为正整数).
解: -yn · yn+1
= (-1)·yn+n+1
= -y2n+1.
例 2
计算:
[教材P3 例题2]
例 3
计算:
(2)(-x)×(-x2)×(-x3);
(1) y · y2 · y4 .
解: y · y2 · y4
= (y · y2) · y4
= y7.
= y3 · y4
或: y · y2 · y4
= y1+2+4
= y7.
解: (-x)×(-x2)×(-x3)
=-(x·x2·x3)
=-x6
或: (-x)×(-x2)×(-x3)
=-x1+2+3
= -x6 .
=-(x3·x3)
[选自教材P3 例题3]
1、公式·=( )中的底数,不仅可以是数、单项式,也可以是多项式等其他代数式;
2、同底数幂相乘时,如果有负号,要注意符号;
3、当底数互为相反数的幂相乘时,先统一底数,再计算。
= ?(m,n,k都是正整数)
=
当三个或三个以上的同底数幂相乘时,同样适用同底数幂的乘法法则,可表示为am·an·ap= (m,n,p为正整数).
1.计算:
(1)56×54;
(2)x · x3;
解: 56×54
= 56+4
= 510.
解: x · x3
= x1+3
= x4.
(3)(-2)3·(-2)4;
(4)-a5 · a5.
解: (-2)3·(-2)4
= (-2)3+4
= (-2)7.
解: -a5 · a5
= -a5+5
= -a10.
(5)xm+1 · xm-1.
解: xm+1 · xm-1
= xm+1+m-1
= x2m.
[教材P4 练习 第1题]
(其中m>1,且m是正整数)
解: (-x)×x3×(-x)5
= (-1)×(-1)×x1+3+5
= x9
2. 计算:
解: x2 · x3 · x4
= x2+3+4
= x9
(2)(-x)×x3×(-x)5;
(1)x2 · x3 · x4 ;
[教材P4 练习 第2题]
解: xn×xn+1×xn+2
= xn+n+1+n+2
= x3n+3
(3)xn · xn+1 · xn+2;(n是正整数)
同底数幂的乘法
幂的运算
am·an= am+n
(m,n都是正整数).
同底数幂相乘,底数不变,指数相加.
第1章 整式的乘法
1.1.1 同底数幂的乘法
1.理解同底数幂的乘法法则.
2.能够运用同底数幂的乘法法则进行相关计算.
a
a
a2
a
a3
= a·a
= a·a·a
2
3
a4
a5
a6
an
= a·a·a·a
= a·a·a·a·a
= a·a·a·a·a·a
= a·a········a
n个
有理数
n
a
an
= a·a········a
n个
求n个相同因数的乘积的运算,叫作乘方.
底数
指数
乘方
幂
≈
n个相同的因数乘积的简便记号,叫作幂.
公元1607年,利玛窦和徐光启合译欧里几得的《原本》时,对“幂”字做了注解:“自乘之数曰幂.”
拓展知识
22×24= ; a2·a4= ;
a3·am= ;(m是正整数)
×
×
比较上述等式两端的底数和指数,你会发现什么?
说一说
底数不变,指数相加.
一般地,若m,n都是正整数,则
也就是
即:同底数幂相乘,底数不变,指数相加.
例 1
计算:
(1)105×103;
(2)x3 · x4.
解: 105×103
= 105+3
= 108.
解: x3 · x4
= x3+4
= x7.
[教材P3 例题1]
下列计算对不对?如果不对,应该怎样改正?
(1) a2 · a5= a10.
(2) a3 · a3= 2a6.
(3) a · a4= a4.
(1) a2 · a5= a7.
(2) a3 · a3= a6.
(3) a · a4= a5.
×
×
×
(1) -a·a3;
解: -a·a3
= (-1)·a1+3
=﹣a4
(2) -y n · y n+1 (n为正整数).
解: -yn · yn+1
= (-1)·yn+n+1
= -y2n+1.
例 2
计算:
[教材P3 例题2]
例 3
计算:
(2)(-x)×(-x2)×(-x3);
(1) y · y2 · y4 .
解: y · y2 · y4
= (y · y2) · y4
= y7.
= y3 · y4
或: y · y2 · y4
= y1+2+4
= y7.
解: (-x)×(-x2)×(-x3)
=-(x·x2·x3)
=-x6
或: (-x)×(-x2)×(-x3)
=-x1+2+3
= -x6 .
=-(x3·x3)
[选自教材P3 例题3]
1、公式·=( )中的底数,不仅可以是数、单项式,也可以是多项式等其他代数式;
2、同底数幂相乘时,如果有负号,要注意符号;
3、当底数互为相反数的幂相乘时,先统一底数,再计算。
= ?(m,n,k都是正整数)
=
当三个或三个以上的同底数幂相乘时,同样适用同底数幂的乘法法则,可表示为am·an·ap= (m,n,p为正整数).
1.计算:
(1)56×54;
(2)x · x3;
解: 56×54
= 56+4
= 510.
解: x · x3
= x1+3
= x4.
(3)(-2)3·(-2)4;
(4)-a5 · a5.
解: (-2)3·(-2)4
= (-2)3+4
= (-2)7.
解: -a5 · a5
= -a5+5
= -a10.
(5)xm+1 · xm-1.
解: xm+1 · xm-1
= xm+1+m-1
= x2m.
[教材P4 练习 第1题]
(其中m>1,且m是正整数)
解: (-x)×x3×(-x)5
= (-1)×(-1)×x1+3+5
= x9
2. 计算:
解: x2 · x3 · x4
= x2+3+4
= x9
(2)(-x)×x3×(-x)5;
(1)x2 · x3 · x4 ;
[教材P4 练习 第2题]
解: xn×xn+1×xn+2
= xn+n+1+n+2
= x3n+3
(3)xn · xn+1 · xn+2;(n是正整数)
同底数幂的乘法
幂的运算
am·an= am+n
(m,n都是正整数).
同底数幂相乘,底数不变,指数相加.
同课章节目录
