北师大版数学八年级上册第五章二元一次方程组第五节《应用二元一次方程组——里程碑上的数》同步练习
文档属性
| 名称 | 北师大版数学八年级上册第五章二元一次方程组第五节《应用二元一次方程组——里程碑上的数》同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 189.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-10 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
北师大版数学八年级上册第五章二元一次方程组第五节应用二元一次方程组——里程碑上的数同步练习
一、选择题
1.买1根油条和3个大饼共7元,买3根油条和1个大饼共5元.下列说法中正确的是( )
A.买1根油条和1个大饼共2.5元
B.2根油条比1个大饼便宜
C.买2根油条和4个大饼共9元
D.买5根油条和7个大饼共19元
答案:D
解析:解答:设1根油条x元,1个大饼y元,根据题意可得:,
解得:,
故买5根油条和7个大饼共19元.
故选:D.
分析:利用买1根油条和3个大饼共7元,买3根油条和1个大饼共5元,分别得出方程求出即可.
2. 依依买了7本数学书和2本语文书共花了100元;菲菲买了4本语文书和2本数学书共花了80元.则买3本数学书要花( )元.
A.30 B.20 C.15 D.45
答案:A
解析:解答:设数学书和语文书的单价分别为x、y元/本,则,
解得,
则3y=3×10=30(元).
故选:A.
分析:设数学书和语文书的单价分别为x、y元/本,依据“7本数学书和2本语文书共花了100元;4本语文书和2本数学书共花了80元”列出方程组,并解答即可求得数学书的单价.
3. 学校组织春游,每人车费4元.一班班长与二班班长的对话如下:
一班班长:我们两班共93人.二班班长:我们二班比你们一班多交了12元的车费.
由上述对话可知,一班和二班的人数分别是( )
A.45,42 B.45,48 C.48,51 D.51,42
答案:B
解析:解答:设一班x人,二班y人,
则
解得:,
即一班45人,二班48人.
故选:B.
分析:设一班x人,二班y人,则根据两班共93人及二班比一班多交了12元的车费可分别列出方程,解出即可.
4. 十一旅游黄金周期间,某景点举办优惠活动,成人票和儿童票均有较大折扣,王明家去了3个大人和4个小孩,共花了400元,李娜家去了4个大人和2个小孩,共花了400元,王斌家计划去3个大人和2个小孩,请你帮助他算一下,需要准备多少门票钱?( )
A.300元 B.310元 C.320元 D.330元
答案:C
解析:解答:设大人门票为x,小孩门票为y,
由题意,得:,
解得:,
则3x+2y=320.
即王斌家计划去3个大人和2个小孩,需要320元的门票.
故选:C.
分析:设大人门票为x,小孩门票为y,根据题目给出的等量关系建立方程组,然后解出x、y的值,再代入计算即可.
5. 一个两位数的十位数字与个位数字之和是7,如果把这个两位数加上45,那么恰好成为把个位数字和十位数字对调后组成的数,那么这个两位数是( )
A.16 B.25 C.52 D.61
答案:A
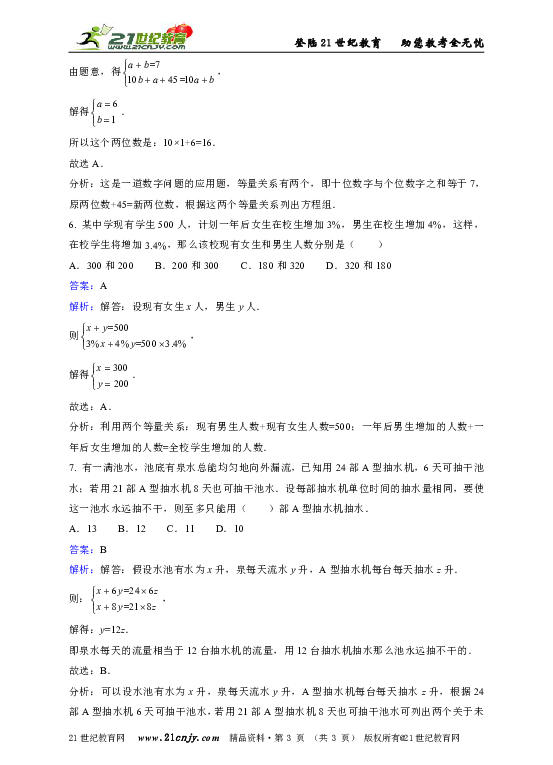
解析:解答:设个位数字为a,十位数字为b,则这个两位数是(10b+a),
由题意,得,
解得.
所以这个两位数是:10×1+6=16.
故选A.
分析:这是一道数字问题的应用题,等量关系有两个,即十位数字与个位数字之和等于7,原两位数+45=新两位数,根据这两个等量关系列出方程组.
6. 某中学现有学生500人,计划一年后女生在校生增加3%,男生在校生增加4%,这样,在校学生将增加3.4%,那么该校现有女生和男生人数分别是( )
A.300和200 B.200和300 C.180和320 D.320和180
答案:A
解析:解答:设现有女生x人,男生y人.
则,
解得.
故选:A.
分析:利用两个等量关系:现有男生人数+现有女生人数=500;一年后男生增加的人数+一年后女生增加的人数=全校学生增加的人数.
7. 有一满池水,池底有泉水总能均匀地向外漏流,已知用24部A型抽水机,6天可抽干池水;若用21部A型抽水机8天也可抽干池水.设每部抽水机单位时间的抽水量相同,要使这一池水永远抽不干,则至多只能用( )部A型抽水机抽水.
A.13 B.12 C.11 D.10
答案:B
解析:解答:假设水池有水为x升,泉每天流水y升,A型抽水机每台每天抽水z升.
则:,
解得:y=12z.
即泉水每天的流量相当于12台抽水机的流量,用12台抽水机抽水那么池永远抽不干的.
故选:B.
分析:可以设水池有水为x升,泉每天流水y升,A型抽水机每台每天抽水z升,根据24部A型抽水机6天可抽干池水,若用21部A型抽水机8天也可抽干池水可列出两个关于未知数的方程,求方程组的解可得到yz之间的关系,即可得解.
8. 若买2支圆珠笔、1本笔记本需14元;买1支圆珠笔,2本笔记本需16元,则买4支圆珠笔、4本笔记本需( )元.
A.30 B.32 C.40 D.42
答案:C
解析:解答:设一支圆珠笔x元,一个笔记本y元,
由题意,得:,
则3(x+y)=30,
所以 x+y=10,
则4(x+y)=40,即买4支圆珠笔,4个笔记本需40元.
故选:C.
分析:设一支圆珠笔x元,一个笔记本y元,根据2支圆珠笔+1个笔记本=4元,1支圆珠笔+2个笔记本=5元,列出方程组,解出可得出答案.
9. 我国古代问题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺,绳长、井深各几何?(注:绳儿折即把绳平均分成几等分.)( )
A.36,8 B.28,6 C.28,8 D.13,3
答案:A
解析:解答:设绳长x米、井深y米,依题意有 ,
解得.
答:绳长36米、井深8米.
故选:A.
分析:此题不变的是井深,用代数式表示井深即可得方程.
此题中的等量关系有:
①将绳三折测之,绳多四尺;
②绳四折测之,绳多一尺.
10. 小明去超市买东西花20元,他身上只带了面值为2元和5元的纸币,营业员没有零钱找给他,那么小明付款有几种方式( )
A.2种 B.3种 C.4种 D.5种
答案:B
解析:解答:设小明付款时2元和5元的纸币分别有x、y张,
∵小明去超市买东西花20元,
∴2x+5y=20,
∴2x=20-5y
而x≥0,y≥0,且x、y是整数,
∴y必须是偶数,
∴y=2,4或0,x=5,0或10.
∴小明付款有三种方式.
故选B.
分析:设小明付款时2元和5元的纸币分别有x、y张,由于小明去超市买东西花20元,由此得到方程2x+5y=20,然后根据x、y都是自然数即可确定x、y的值.
11. 某商店经销一种商品,由于进价降低了5%,出售价不变,使得利润由m%提高到(m+6)%,则m的值为( )
A.10 B.12 C.14 D.17
答案:C
解析:解答:设原进价为x,则:
x+m% x=95% x+95% x (m+6)%,
∴1+m%=95%+95%(m+6)%,
∴100+m=95+0.95(m+6),
∴0.05m=0.7
解得:m=14.
故选C.
分析:本题中,因为售价=进价+利润,所以等量关系是:原进价+原来利润=进价降低后的进价+降价后的利润.
12. 小刚去距县城28千米的旅游点游玩,先乘车,后步行.全程共用了1小时,已知汽车速度为每小时36千米,步行的速度每小时4千米,则小刚乘车路程和步行路程分别是( )
A.26千米,2千米 B.27千米,1千米
C.25千米,3千米 D.24千米,4千米
答案:B
解析:解答:设小刚乘车路程为x千米,步行路程y千米,由题意得: ,
解得:.
故选:B.
分析:设小刚乘车路程为x千米,步行路程y千米,根据题意可得等量关系:①步行路程+乘车路程=28千米;②汽车行驶x千米时间+步行y千米的时间=1小时,根据题意列出方程组即可.
13. 把面值为2元的纸币换成1角、5角都有的硬币,共有几种换法( )
A.2种 B.3种 C.4种 D.5种
答案:B
解析:解答:设1角的个数为x个,5角的个数为y个.
则 ,
解得
故共有3种换法.
故选B.
分析:该问题中有两个未知量但只能列出一个方程等式,可将一个未知量看成一个常量,解出另一个未知量,且两个未知量都是正整数.本题中等量关系是若干个一角和五角等于2元.同时一角和五角的个数不为0.
14. 一张试卷有25道选择题,做对一题得4分,做错一题扣一分,小明做了全部试题,得70分,则他做对了( )
A.17题 B.18题 C.19题 D.20题
答案:C
解析:解答:设做对了x道,做错了y道,
则,
解得.
即答对了19道.
故选:C.
分析:首先假设做对x道题,做错y道题.等量关系:①共25道选择题;②一共得70分.
15. 某中学生足球联赛8轮(即每队平均赛8场),胜一场3分,平一场得1分,负一场得0分.在这次足球联赛中,某队踢平的场数是所负场数的2倍,共得17分,则该队胜的场数是( )
A.5场 B.4场 C.3场 D.2场
答案:A
解析:解答:设负的场数为x,胜的场数为y,由题意得,
解得,
则胜了5场.
故选:A.
分析:设负的场数为x,胜的场数为y,则平的场数为2x,等量关系为:胜的场数的得分+平的场数的得分=17,胜场数+平场数+负场数=8,把相关数值代入求解即可.
二、填空题
16. 端午节时,王老师用72元钱买了荷包和五彩绳共20个,其中荷包每个4元,五彩绳每个3元.设王老师买荷包x个,五彩绳y个,根据题意,列出的方程组为
答案:
解析:解答:根据题意可得,
故答案是.
分析:根据荷包个数+五彩绳个数=20,以及荷包价钱+五彩绳价钱=72,列式即可.
17. 某单位招聘员工采取笔试与面试相结合的方式进行,两项成绩满分均为100分.根据规定,笔试成绩和面试成绩分别按一定的百分比折合综合成绩(综合成绩的满分仍为100分).已知小明应聘的笔试成绩为85分,面试成绩为90分,现得知小明的最后综合成绩为88分.设小明的笔试成绩所占的百分比为x,面试成绩所占的百分比为y,根据题意列方程组得
答案:
解析:解答:设小明的笔试成绩所占的百分比为x,面试成绩所占的百分比为y,
由题意得,.
故答案为: .
分析:设小明的笔试成绩所占的百分比为x,面试成绩所占的百分比为y,根据题意可知:笔试成绩所占的百分比和面试成绩所占的百分比之和为1,小明的最后综合成绩为88分,列方程组求解.
18. 某校举行“中国梦 劳动美”知识竞赛,其评分规则如下:答对一题得5分,答错一题得-5分,不作答得0分.已知试题共20道,满分100分,凡优秀(得分80分或以上)者才有资格参加决赛.小明同学在这次竞赛中有2道题未答,但刚好获得决赛资格.设小明答对x道题,答题y道题,则可列出满足题意的方程组为
答案:
解析:解答:设小明答对x道题,答题y道题,由题意得:,
故答案为:.
分析:根据题意可得等量关系:①答对题数+答错题数=20道;②5×答对题数-5×答错题数=80分,根据等量关系列出方程组即可.
19. 一个两位数的十位数字与个位数字之和等于5,十位数字与个位数字之差为1,设十位数字为x,个位数字为y,则用方程组表示上述语言为
答案:
解析:解答:由题意,有.
分析:题中有两个等量关系:十位数字+个位数字=5;十位数字-个位数字=1.
根据这两个等量关系即可列出方程组.
20. 某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人.设运动员人数为x人,组数为y组,可列方程组为
答案:
解析:解答:设运动员人数为x人,组数为y组,由题意得:.
故答案为: .
分析:根据关键语句“若每组7人,余3人”可得方程7y+3-x;“若每组8人,则缺5人.”可得方程8y-5=x,联立两个方程可得方程组.
三、解答题
21. 已知A,B两件服装的成本共500元,鑫洋服装店老板分别以30%和20%的利润率定价后进行销售,该服装店共获利130元,问A,B两件服装的成本各是多少元?
答案:A服装成本为300元,B服装成本200元.
解析:解答:设A服装成本为x元,B服装成本y元,由题意得:,
解得:,
答:A服装成本为300元,B服装成本200元.
分析:设A服装成本为x元,B服装成本y元,由题意得等量关系:①成本共500元;②共获利130元,根据等量关系列出方程组,再解即可.
22. 假如娄底市的出租车是这样收费的:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费.
小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底汽车站走了6.5千米,付车费14.5元.”
问:(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?(2)小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费多少元?
答案:(1)出租车的起步价是元,超过1.5千米后每千米收费2元;
(2)小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费12.5元.
解析:解答:(1)设出租车的起步价是x元,超过1.5千米后每千米收费y元.
依题意得,,
解得.
答:出租车的起步价是元,超过1.5千米后每千米收费2元;
(2)+(5.5-1.5)×2=12.5(元).
答:小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费12.5元.
分析:(1)设出租车的起步价是x元,超过1.5千米后每千米收费y元.根据他们的对话列出方程组并解答;(2)5.5千米分两段收费:1.5千米、(5.5-1.5)千米.根据(1)中的单价进行计算.
23. 我市某超市举行店庆活动,对甲、乙两种商品实行打折销售,打折前,购买2件甲商品和3件乙商品需要180元;购买1件甲商品和4件乙商品需要200元,而店庆期间,购买10件甲商品和10件乙商品仅需520元,这比打折前少花多少钱?
答案:这比不打折前少花160元.
解析:解:设打折前甲商品的单价为x元,乙商品的单价为y元,
由题意得:,
解得:.
则购买10件甲商品和10件乙商品需要520元,
∵打折后实际花费:10×(24+44)=680(元),
∴这比不打折前少花160元.
答:这比不打折前少花160元.
分析:设甲商品单价为x元,乙商品单价为y元,根据购买3件甲商品和1件乙商品需用180元;购买1件甲商品和4件乙商品需用200元,列出方程组,继而可计算购买10件甲商品和10件乙商品需要的花费,也可得出比不打折前少花多少钱.
24. 某中学男、女生大小宿舍的床位个数都分别相同.其中男生164人,住10间大宿舍和8间小宿舍,刚好住满;女生200人,住12间大宿舍和10间小宿舍,也刚好住满.求该校大小宿舍每间各住多少人?
答案:该校的大小宿舍每间分别住10人、8人.
解析:解答:设该校的大小宿舍每间分别住x人、y人.
由题意,得,
解这个方程,得.
答:该校的大小宿舍每间分别住10人、8人.
分析:设该校的大小宿舍每间分别住x人、y人.根据“男生164人,住10间大宿舍和8间小宿舍,刚好住满;女生200人,住12间大宿舍和10间小宿舍,也刚好住满”列出方程组,并解答.
25. 随着人们环保意识的增强,“低碳生活”成为人们提倡的生活方式.黄先生要从某地到福州,若乘飞机需要3小时,乘汽车需要9小时.这两种交通工具每小时排放的二氧化碳总量为70千克,已知飞机每小时二氧化碳的排放量比汽车多44千克,黄先生若乘汽车来福州,那么他此行与乘飞机相比将减少二氧化碳排放量多少千克?
答案:他此行将减少二氧化碳排放量54千克.
解析:解答:设黄先生乘飞机和坐汽车每小时二氧化碳的排放量分别为x千克和y千克,依题意得:,
解得,
3x-9y=54,
答:他此行将减少二氧化碳排放量54千克.
分析:此题可以设两种交通工具每小时二氧化碳的排放量分别为x和y,根据已知两个关系列二元一次方程组,那么减少二氧化碳排放量是3x-9y.解二元一次方程组求出x和y代入即可求出.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 11 页 (共 11 页) 版权所有@21世纪教育网
北师大版数学八年级上册第五章二元一次方程组第五节应用二元一次方程组——里程碑上的数同步练习
一、选择题
1.买1根油条和3个大饼共7元,买3根油条和1个大饼共5元.下列说法中正确的是( )
A.买1根油条和1个大饼共2.5元
B.2根油条比1个大饼便宜
C.买2根油条和4个大饼共9元
D.买5根油条和7个大饼共19元
答案:D
解析:解答:设1根油条x元,1个大饼y元,根据题意可得:,
解得:,
故买5根油条和7个大饼共19元.
故选:D.
分析:利用买1根油条和3个大饼共7元,买3根油条和1个大饼共5元,分别得出方程求出即可.
2. 依依买了7本数学书和2本语文书共花了100元;菲菲买了4本语文书和2本数学书共花了80元.则买3本数学书要花( )元.
A.30 B.20 C.15 D.45
答案:A
解析:解答:设数学书和语文书的单价分别为x、y元/本,则,
解得,
则3y=3×10=30(元).
故选:A.
分析:设数学书和语文书的单价分别为x、y元/本,依据“7本数学书和2本语文书共花了100元;4本语文书和2本数学书共花了80元”列出方程组,并解答即可求得数学书的单价.
3. 学校组织春游,每人车费4元.一班班长与二班班长的对话如下:
一班班长:我们两班共93人.二班班长:我们二班比你们一班多交了12元的车费.
由上述对话可知,一班和二班的人数分别是( )
A.45,42 B.45,48 C.48,51 D.51,42
答案:B
解析:解答:设一班x人,二班y人,
则
解得:,
即一班45人,二班48人.
故选:B.
分析:设一班x人,二班y人,则根据两班共93人及二班比一班多交了12元的车费可分别列出方程,解出即可.
4. 十一旅游黄金周期间,某景点举办优惠活动,成人票和儿童票均有较大折扣,王明家去了3个大人和4个小孩,共花了400元,李娜家去了4个大人和2个小孩,共花了400元,王斌家计划去3个大人和2个小孩,请你帮助他算一下,需要准备多少门票钱?( )
A.300元 B.310元 C.320元 D.330元
答案:C
解析:解答:设大人门票为x,小孩门票为y,
由题意,得:,
解得:,
则3x+2y=320.
即王斌家计划去3个大人和2个小孩,需要320元的门票.
故选:C.
分析:设大人门票为x,小孩门票为y,根据题目给出的等量关系建立方程组,然后解出x、y的值,再代入计算即可.
5. 一个两位数的十位数字与个位数字之和是7,如果把这个两位数加上45,那么恰好成为把个位数字和十位数字对调后组成的数,那么这个两位数是( )
A.16 B.25 C.52 D.61
答案:A
解析:解答:设个位数字为a,十位数字为b,则这个两位数是(10b+a),
由题意,得,
解得.
所以这个两位数是:10×1+6=16.
故选A.
分析:这是一道数字问题的应用题,等量关系有两个,即十位数字与个位数字之和等于7,原两位数+45=新两位数,根据这两个等量关系列出方程组.
6. 某中学现有学生500人,计划一年后女生在校生增加3%,男生在校生增加4%,这样,在校学生将增加3.4%,那么该校现有女生和男生人数分别是( )
A.300和200 B.200和300 C.180和320 D.320和180
答案:A
解析:解答:设现有女生x人,男生y人.
则,
解得.
故选:A.
分析:利用两个等量关系:现有男生人数+现有女生人数=500;一年后男生增加的人数+一年后女生增加的人数=全校学生增加的人数.
7. 有一满池水,池底有泉水总能均匀地向外漏流,已知用24部A型抽水机,6天可抽干池水;若用21部A型抽水机8天也可抽干池水.设每部抽水机单位时间的抽水量相同,要使这一池水永远抽不干,则至多只能用( )部A型抽水机抽水.
A.13 B.12 C.11 D.10
答案:B
解析:解答:假设水池有水为x升,泉每天流水y升,A型抽水机每台每天抽水z升.
则:,
解得:y=12z.
即泉水每天的流量相当于12台抽水机的流量,用12台抽水机抽水那么池永远抽不干的.
故选:B.
分析:可以设水池有水为x升,泉每天流水y升,A型抽水机每台每天抽水z升,根据24部A型抽水机6天可抽干池水,若用21部A型抽水机8天也可抽干池水可列出两个关于未知数的方程,求方程组的解可得到yz之间的关系,即可得解.
8. 若买2支圆珠笔、1本笔记本需14元;买1支圆珠笔,2本笔记本需16元,则买4支圆珠笔、4本笔记本需( )元.
A.30 B.32 C.40 D.42
答案:C
解析:解答:设一支圆珠笔x元,一个笔记本y元,
由题意,得:,
则3(x+y)=30,
所以 x+y=10,
则4(x+y)=40,即买4支圆珠笔,4个笔记本需40元.
故选:C.
分析:设一支圆珠笔x元,一个笔记本y元,根据2支圆珠笔+1个笔记本=4元,1支圆珠笔+2个笔记本=5元,列出方程组,解出可得出答案.
9. 我国古代问题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺,绳长、井深各几何?(注:绳儿折即把绳平均分成几等分.)( )
A.36,8 B.28,6 C.28,8 D.13,3
答案:A
解析:解答:设绳长x米、井深y米,依题意有 ,
解得.
答:绳长36米、井深8米.
故选:A.
分析:此题不变的是井深,用代数式表示井深即可得方程.
此题中的等量关系有:
①将绳三折测之,绳多四尺;
②绳四折测之,绳多一尺.
10. 小明去超市买东西花20元,他身上只带了面值为2元和5元的纸币,营业员没有零钱找给他,那么小明付款有几种方式( )
A.2种 B.3种 C.4种 D.5种
答案:B
解析:解答:设小明付款时2元和5元的纸币分别有x、y张,
∵小明去超市买东西花20元,
∴2x+5y=20,
∴2x=20-5y
而x≥0,y≥0,且x、y是整数,
∴y必须是偶数,
∴y=2,4或0,x=5,0或10.
∴小明付款有三种方式.
故选B.
分析:设小明付款时2元和5元的纸币分别有x、y张,由于小明去超市买东西花20元,由此得到方程2x+5y=20,然后根据x、y都是自然数即可确定x、y的值.
11. 某商店经销一种商品,由于进价降低了5%,出售价不变,使得利润由m%提高到(m+6)%,则m的值为( )
A.10 B.12 C.14 D.17
答案:C
解析:解答:设原进价为x,则:
x+m% x=95% x+95% x (m+6)%,
∴1+m%=95%+95%(m+6)%,
∴100+m=95+0.95(m+6),
∴0.05m=0.7
解得:m=14.
故选C.
分析:本题中,因为售价=进价+利润,所以等量关系是:原进价+原来利润=进价降低后的进价+降价后的利润.
12. 小刚去距县城28千米的旅游点游玩,先乘车,后步行.全程共用了1小时,已知汽车速度为每小时36千米,步行的速度每小时4千米,则小刚乘车路程和步行路程分别是( )
A.26千米,2千米 B.27千米,1千米
C.25千米,3千米 D.24千米,4千米
答案:B
解析:解答:设小刚乘车路程为x千米,步行路程y千米,由题意得: ,
解得:.
故选:B.
分析:设小刚乘车路程为x千米,步行路程y千米,根据题意可得等量关系:①步行路程+乘车路程=28千米;②汽车行驶x千米时间+步行y千米的时间=1小时,根据题意列出方程组即可.
13. 把面值为2元的纸币换成1角、5角都有的硬币,共有几种换法( )
A.2种 B.3种 C.4种 D.5种
答案:B
解析:解答:设1角的个数为x个,5角的个数为y个.
则 ,
解得
故共有3种换法.
故选B.
分析:该问题中有两个未知量但只能列出一个方程等式,可将一个未知量看成一个常量,解出另一个未知量,且两个未知量都是正整数.本题中等量关系是若干个一角和五角等于2元.同时一角和五角的个数不为0.
14. 一张试卷有25道选择题,做对一题得4分,做错一题扣一分,小明做了全部试题,得70分,则他做对了( )
A.17题 B.18题 C.19题 D.20题
答案:C
解析:解答:设做对了x道,做错了y道,
则,
解得.
即答对了19道.
故选:C.
分析:首先假设做对x道题,做错y道题.等量关系:①共25道选择题;②一共得70分.
15. 某中学生足球联赛8轮(即每队平均赛8场),胜一场3分,平一场得1分,负一场得0分.在这次足球联赛中,某队踢平的场数是所负场数的2倍,共得17分,则该队胜的场数是( )
A.5场 B.4场 C.3场 D.2场
答案:A
解析:解答:设负的场数为x,胜的场数为y,由题意得,
解得,
则胜了5场.
故选:A.
分析:设负的场数为x,胜的场数为y,则平的场数为2x,等量关系为:胜的场数的得分+平的场数的得分=17,胜场数+平场数+负场数=8,把相关数值代入求解即可.
二、填空题
16. 端午节时,王老师用72元钱买了荷包和五彩绳共20个,其中荷包每个4元,五彩绳每个3元.设王老师买荷包x个,五彩绳y个,根据题意,列出的方程组为
答案:
解析:解答:根据题意可得,
故答案是.
分析:根据荷包个数+五彩绳个数=20,以及荷包价钱+五彩绳价钱=72,列式即可.
17. 某单位招聘员工采取笔试与面试相结合的方式进行,两项成绩满分均为100分.根据规定,笔试成绩和面试成绩分别按一定的百分比折合综合成绩(综合成绩的满分仍为100分).已知小明应聘的笔试成绩为85分,面试成绩为90分,现得知小明的最后综合成绩为88分.设小明的笔试成绩所占的百分比为x,面试成绩所占的百分比为y,根据题意列方程组得
答案:
解析:解答:设小明的笔试成绩所占的百分比为x,面试成绩所占的百分比为y,
由题意得,.
故答案为: .
分析:设小明的笔试成绩所占的百分比为x,面试成绩所占的百分比为y,根据题意可知:笔试成绩所占的百分比和面试成绩所占的百分比之和为1,小明的最后综合成绩为88分,列方程组求解.
18. 某校举行“中国梦 劳动美”知识竞赛,其评分规则如下:答对一题得5分,答错一题得-5分,不作答得0分.已知试题共20道,满分100分,凡优秀(得分80分或以上)者才有资格参加决赛.小明同学在这次竞赛中有2道题未答,但刚好获得决赛资格.设小明答对x道题,答题y道题,则可列出满足题意的方程组为
答案:
解析:解答:设小明答对x道题,答题y道题,由题意得:,
故答案为:.
分析:根据题意可得等量关系:①答对题数+答错题数=20道;②5×答对题数-5×答错题数=80分,根据等量关系列出方程组即可.
19. 一个两位数的十位数字与个位数字之和等于5,十位数字与个位数字之差为1,设十位数字为x,个位数字为y,则用方程组表示上述语言为
答案:
解析:解答:由题意,有.
分析:题中有两个等量关系:十位数字+个位数字=5;十位数字-个位数字=1.
根据这两个等量关系即可列出方程组.
20. 某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人.设运动员人数为x人,组数为y组,可列方程组为
答案:
解析:解答:设运动员人数为x人,组数为y组,由题意得:.
故答案为: .
分析:根据关键语句“若每组7人,余3人”可得方程7y+3-x;“若每组8人,则缺5人.”可得方程8y-5=x,联立两个方程可得方程组.
三、解答题
21. 已知A,B两件服装的成本共500元,鑫洋服装店老板分别以30%和20%的利润率定价后进行销售,该服装店共获利130元,问A,B两件服装的成本各是多少元?
答案:A服装成本为300元,B服装成本200元.
解析:解答:设A服装成本为x元,B服装成本y元,由题意得:,
解得:,
答:A服装成本为300元,B服装成本200元.
分析:设A服装成本为x元,B服装成本y元,由题意得等量关系:①成本共500元;②共获利130元,根据等量关系列出方程组,再解即可.
22. 假如娄底市的出租车是这样收费的:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费.
小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底汽车站走了6.5千米,付车费14.5元.”
问:(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?(2)小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费多少元?
答案:(1)出租车的起步价是元,超过1.5千米后每千米收费2元;
(2)小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费12.5元.
解析:解答:(1)设出租车的起步价是x元,超过1.5千米后每千米收费y元.
依题意得,,
解得.
答:出租车的起步价是元,超过1.5千米后每千米收费2元;
(2)+(5.5-1.5)×2=12.5(元).
答:小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费12.5元.
分析:(1)设出租车的起步价是x元,超过1.5千米后每千米收费y元.根据他们的对话列出方程组并解答;(2)5.5千米分两段收费:1.5千米、(5.5-1.5)千米.根据(1)中的单价进行计算.
23. 我市某超市举行店庆活动,对甲、乙两种商品实行打折销售,打折前,购买2件甲商品和3件乙商品需要180元;购买1件甲商品和4件乙商品需要200元,而店庆期间,购买10件甲商品和10件乙商品仅需520元,这比打折前少花多少钱?
答案:这比不打折前少花160元.
解析:解:设打折前甲商品的单价为x元,乙商品的单价为y元,
由题意得:,
解得:.
则购买10件甲商品和10件乙商品需要520元,
∵打折后实际花费:10×(24+44)=680(元),
∴这比不打折前少花160元.
答:这比不打折前少花160元.
分析:设甲商品单价为x元,乙商品单价为y元,根据购买3件甲商品和1件乙商品需用180元;购买1件甲商品和4件乙商品需用200元,列出方程组,继而可计算购买10件甲商品和10件乙商品需要的花费,也可得出比不打折前少花多少钱.
24. 某中学男、女生大小宿舍的床位个数都分别相同.其中男生164人,住10间大宿舍和8间小宿舍,刚好住满;女生200人,住12间大宿舍和10间小宿舍,也刚好住满.求该校大小宿舍每间各住多少人?
答案:该校的大小宿舍每间分别住10人、8人.
解析:解答:设该校的大小宿舍每间分别住x人、y人.
由题意,得,
解这个方程,得.
答:该校的大小宿舍每间分别住10人、8人.
分析:设该校的大小宿舍每间分别住x人、y人.根据“男生164人,住10间大宿舍和8间小宿舍,刚好住满;女生200人,住12间大宿舍和10间小宿舍,也刚好住满”列出方程组,并解答.
25. 随着人们环保意识的增强,“低碳生活”成为人们提倡的生活方式.黄先生要从某地到福州,若乘飞机需要3小时,乘汽车需要9小时.这两种交通工具每小时排放的二氧化碳总量为70千克,已知飞机每小时二氧化碳的排放量比汽车多44千克,黄先生若乘汽车来福州,那么他此行与乘飞机相比将减少二氧化碳排放量多少千克?
答案:他此行将减少二氧化碳排放量54千克.
解析:解答:设黄先生乘飞机和坐汽车每小时二氧化碳的排放量分别为x千克和y千克,依题意得:,
解得,
3x-9y=54,
答:他此行将减少二氧化碳排放量54千克.
分析:此题可以设两种交通工具每小时二氧化碳的排放量分别为x和y,根据已知两个关系列二元一次方程组,那么减少二氧化碳排放量是3x-9y.解二元一次方程组求出x和y代入即可求出.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 11 页 (共 11 页) 版权所有@21世纪教育网
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
