1.5 二次函数的应用 课件(共23张PPT)2024-2025学年湘教版初中数学九年级下册
文档属性
| 名称 | 1.5 二次函数的应用 课件(共23张PPT)2024-2025学年湘教版初中数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 408.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-07 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
第1章 二次函数
1.5 二次函数的应用
1.会分析实际问题中的数量关系和变化规律,能建立二次函数模型(包括确定二次函数的表达式)来解决简单的实际问题.(重点)2.体会数形结合在解决实际问题中的作用,能运用二次函数的性质解决最值问题.(难点)
3.经历函数建模的过程,体会函数建模的方法和思想,进一步提高应用意识.
学习目标
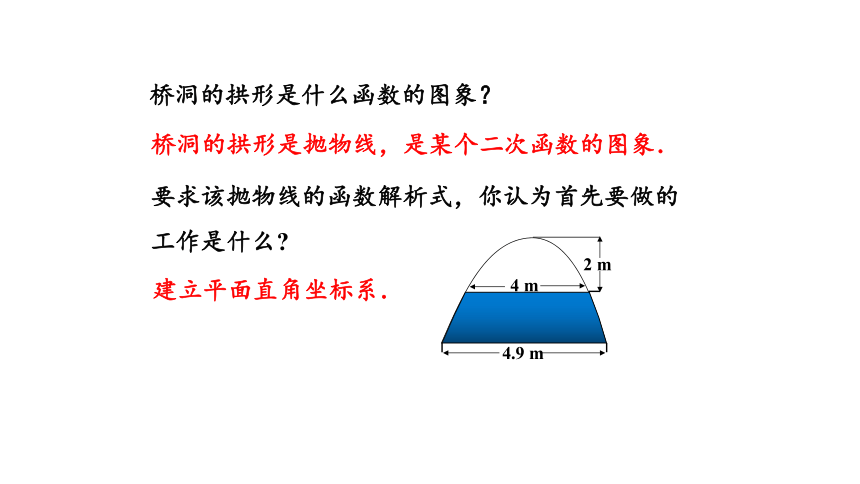
如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9 m,当水面宽4 m时,拱顶离水面2 m.若想了解水面宽度变化时,拱顶离水面高度怎样变化,你能解决这个问题吗?
桥洞的拱形是什么函数的图象?
桥洞的拱形是抛物线,是某个二次函数的图象.
要求该抛物线的函数解析式,你认为首先要做的工作是什么
建立平面直角坐标系.
4 m
2 m
4.9 m
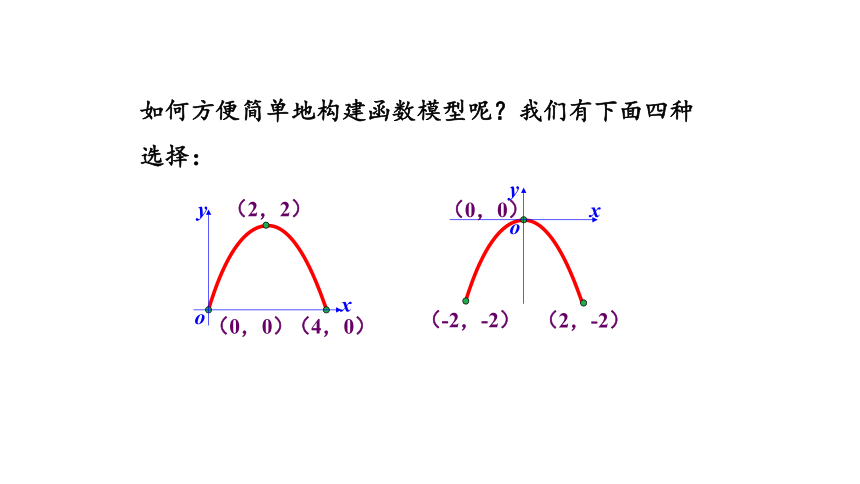
如何方便简单地构建函数模型呢?我们有下面四种选择:
(0,0)
(4,0)
(2,2)
y
o
x
o
y
x
(0,0)
(2,-2)
(-2,-2)
o
y
x
(2,0)
(2,0)
(-2,0)
(0,0)
(-4,0)
(-2,2)
o
y
x
选择哪个更容易解决问题?
由于第二种建立坐标系的顶点坐标是(0,0),因此这个二次函数的形式是y=ax2.这样建立的直角坐标系函数解析式最为简单.
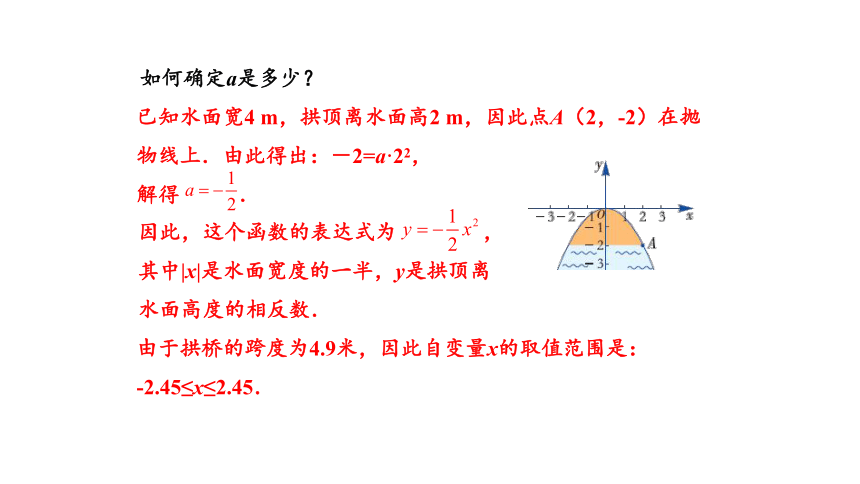
如何确定a是多少?
已知水面宽4 m,拱顶离水面高2 m,因此点A(2,-2)在抛物线上.由此得出:-2=a·22,
解得 .
因此,这个函数的表达式为 ,
其中|x|是水面宽度的一半,y是拱顶离
水面高度的相反数.
由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
-2.45≤x≤2.45.
当水面宽 4.6 m 时, 拱顶离水面几米?
解:当水面宽 4.6 m 时,把x=2.3代入函数的表达式
,得y=-2.645.
答:当水面宽 4.6 m 时,拱顶离水面2.645米.
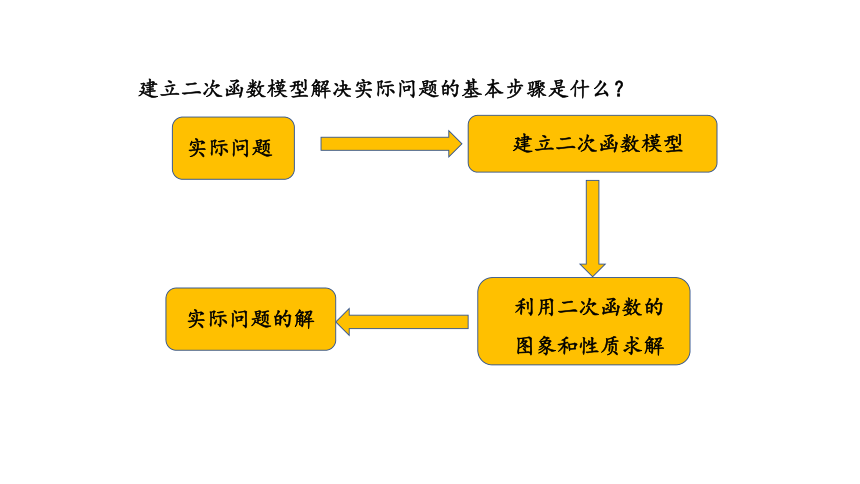
建立二次函数模型解决实际问题的基本步骤是什么?
实际问题
建立二次函数模型
利用二次函数的
图象和性质求解
实际问题的解
如图 , 用 8 m 长的铝材做一个日字形窗框. 试问: 窗框的宽和高各为多少时, 窗框的透光面积 S(m2)最大? 最大面积是多少? (假设铝材的宽度不计)
解:设窗框的宽度为x m.则窗框的高为 m,
其中 .
则窗框的透光面积为: ,
.
配方得: , .
这时高为: .
所以当窗户宽 米,高2米时,透光面积最大,
最大面积为 m2.
所以,当 时,S取最大值 .
要考虑 是不是在自变量x的取值范围内.
运用二次函数求实际问题中的最大值或最小值解题的一般步骤是怎样的?
1、应当求出函数解析式和自变量的取值范围.
3、确定所求得的最大值或最小值对应的字变量的值必须在自变量的取值范围内.
2、通过配方变形,或利用公式求它的最大值或最小值.
例 某网络玩具店引进一批进价为 20 元 / 件的玩具, 如果以单价 30 元销售, 那么一个月内可售出 180 件. 根据销售经验, 提高销售单价会导致销售量的下降, 即销售单价每上涨 1 元, 月销售量将相应减少 10 件. 当销售单价为多少元时, 该店能在一个月内获得最大利润?
解:设每件商品的销售单价上涨 x 元, 一个月内获取的商品总利润为 y 元.每月减少的销售量为10 x(件), 实际销售量为(180 - 10 x)件, 单件利润为(30 + x - 20 )元, 则
y = ( 10 + x ) ( 180 - 10x ) ,
即 y = - 10x2 + 80x + 1 800 ( x ≤ 18 ) .
将上式进行配方,y = - 10x2 + 80x + 1 800
= - 10 ( x - 4 )2 + 1 960.
当x=4时,即销售单价为34元时,y最大值为1960元.
答:当销售单价定为34元时,该店一个月内最大利润为1960元.
你还有什么方法能求出当销售单价为多少元时, 该店能在一个月内获得最大利润?
解:当 时,y有最大值
.
答:商店销售单价应定为70元时,销售利润最大.
建立二次实际问题的一般步骤:
(5)根据求得的解析式进一步分析,判断并进行有关的计算.
(1)根据题意建立适当的平面直角坐标系.
(2)把已知条件转化为点的坐标.
(3)合理设出函数解析式.
(4)利用待定系数法求出函数解析式.
1、如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一根绳子的两端栓于立柱与铁杠结合处,绳子自然下垂呈抛物线状.一身高0.7米的小孩站在离立柱0.4米处,其头部刚好触绳子,求绳子最低点到地面的距离.
A
B
C
D
0.7
1.6
2.2
0.4
E
F
O
x
y
解:以CD所在的直线为x轴,CD的中垂线为y轴建立直角坐标系 则 B(0.8,2.2),F(- 0.4, 0.7).
设 y = ax2 + k,从而有 ,
解得 .
所以, . E坐标为(0,0.2).
故绳子最低点到地面的距离为0.2米.
答:绳子最低点到地面的距离为0.2米.
A
B
C
D
0.7
1.6
2.2
0.4
E
F
O
x
y
2、小红想将一根72cm长的彩带剪成两段,分别围成两个正方形,则她要怎么剪才能让这两个正方形的面积和最小?此时的面积和为多少?
解:设一个正方形的边长为a cm,则另一个正方形的边长为
=(18-a)cm.则两个正方形的面积和为:
S=a2+(18-a)2=2a2-36a+324(0<x<18).
将上式进行配方得:S=2(a-9)2+162(0<x<18).
当a=9 cm时,S最小,最小值为162 cm2.此时,她将彩带二等分.
答:她应将彩带分成相等的两段剪,此时的面积和为162 cm2.
3、某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单位每涨1元,月销售量就减少10千克.
(1)设销售单价为每千克x元,月销售利润为y元,求y与x的函数表达式(不必写出x的取值范围);
(2)商店销售单价应定为多少、销售利润最大?
解:(1)可卖出千克数为500-10(x-50)=1000-10x,
y与x的函数表达式为y=(x-40)(1000-10x)
=-10x2+1400x-40000,
(2)当 时,y有最大值.
答:商店销售单价应定为70元时,销售利润最大.
用抛物线的知识解决生活中的一些实际问题一般步骤:
生活中的一些实际问题
弄清题中量与量之间的依赖关系
建立函数模型
利用二次函数图象和性质解决实际问题
注意自变量的取值范围
第1章 二次函数
1.5 二次函数的应用
1.会分析实际问题中的数量关系和变化规律,能建立二次函数模型(包括确定二次函数的表达式)来解决简单的实际问题.(重点)2.体会数形结合在解决实际问题中的作用,能运用二次函数的性质解决最值问题.(难点)
3.经历函数建模的过程,体会函数建模的方法和思想,进一步提高应用意识.
学习目标
如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9 m,当水面宽4 m时,拱顶离水面2 m.若想了解水面宽度变化时,拱顶离水面高度怎样变化,你能解决这个问题吗?
桥洞的拱形是什么函数的图象?
桥洞的拱形是抛物线,是某个二次函数的图象.
要求该抛物线的函数解析式,你认为首先要做的工作是什么
建立平面直角坐标系.
4 m
2 m
4.9 m
如何方便简单地构建函数模型呢?我们有下面四种选择:
(0,0)
(4,0)
(2,2)
y
o
x
o
y
x
(0,0)
(2,-2)
(-2,-2)
o
y
x
(2,0)
(2,0)
(-2,0)
(0,0)
(-4,0)
(-2,2)
o
y
x
选择哪个更容易解决问题?
由于第二种建立坐标系的顶点坐标是(0,0),因此这个二次函数的形式是y=ax2.这样建立的直角坐标系函数解析式最为简单.
如何确定a是多少?
已知水面宽4 m,拱顶离水面高2 m,因此点A(2,-2)在抛物线上.由此得出:-2=a·22,
解得 .
因此,这个函数的表达式为 ,
其中|x|是水面宽度的一半,y是拱顶离
水面高度的相反数.
由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
-2.45≤x≤2.45.
当水面宽 4.6 m 时, 拱顶离水面几米?
解:当水面宽 4.6 m 时,把x=2.3代入函数的表达式
,得y=-2.645.
答:当水面宽 4.6 m 时,拱顶离水面2.645米.
建立二次函数模型解决实际问题的基本步骤是什么?
实际问题
建立二次函数模型
利用二次函数的
图象和性质求解
实际问题的解
如图 , 用 8 m 长的铝材做一个日字形窗框. 试问: 窗框的宽和高各为多少时, 窗框的透光面积 S(m2)最大? 最大面积是多少? (假设铝材的宽度不计)
解:设窗框的宽度为x m.则窗框的高为 m,
其中 .
则窗框的透光面积为: ,
.
配方得: , .
这时高为: .
所以当窗户宽 米,高2米时,透光面积最大,
最大面积为 m2.
所以,当 时,S取最大值 .
要考虑 是不是在自变量x的取值范围内.
运用二次函数求实际问题中的最大值或最小值解题的一般步骤是怎样的?
1、应当求出函数解析式和自变量的取值范围.
3、确定所求得的最大值或最小值对应的字变量的值必须在自变量的取值范围内.
2、通过配方变形,或利用公式求它的最大值或最小值.
例 某网络玩具店引进一批进价为 20 元 / 件的玩具, 如果以单价 30 元销售, 那么一个月内可售出 180 件. 根据销售经验, 提高销售单价会导致销售量的下降, 即销售单价每上涨 1 元, 月销售量将相应减少 10 件. 当销售单价为多少元时, 该店能在一个月内获得最大利润?
解:设每件商品的销售单价上涨 x 元, 一个月内获取的商品总利润为 y 元.每月减少的销售量为10 x(件), 实际销售量为(180 - 10 x)件, 单件利润为(30 + x - 20 )元, 则
y = ( 10 + x ) ( 180 - 10x ) ,
即 y = - 10x2 + 80x + 1 800 ( x ≤ 18 ) .
将上式进行配方,y = - 10x2 + 80x + 1 800
= - 10 ( x - 4 )2 + 1 960.
当x=4时,即销售单价为34元时,y最大值为1960元.
答:当销售单价定为34元时,该店一个月内最大利润为1960元.
你还有什么方法能求出当销售单价为多少元时, 该店能在一个月内获得最大利润?
解:当 时,y有最大值
.
答:商店销售单价应定为70元时,销售利润最大.
建立二次实际问题的一般步骤:
(5)根据求得的解析式进一步分析,判断并进行有关的计算.
(1)根据题意建立适当的平面直角坐标系.
(2)把已知条件转化为点的坐标.
(3)合理设出函数解析式.
(4)利用待定系数法求出函数解析式.
1、如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一根绳子的两端栓于立柱与铁杠结合处,绳子自然下垂呈抛物线状.一身高0.7米的小孩站在离立柱0.4米处,其头部刚好触绳子,求绳子最低点到地面的距离.
A
B
C
D
0.7
1.6
2.2
0.4
E
F
O
x
y
解:以CD所在的直线为x轴,CD的中垂线为y轴建立直角坐标系 则 B(0.8,2.2),F(- 0.4, 0.7).
设 y = ax2 + k,从而有 ,
解得 .
所以, . E坐标为(0,0.2).
故绳子最低点到地面的距离为0.2米.
答:绳子最低点到地面的距离为0.2米.
A
B
C
D
0.7
1.6
2.2
0.4
E
F
O
x
y
2、小红想将一根72cm长的彩带剪成两段,分别围成两个正方形,则她要怎么剪才能让这两个正方形的面积和最小?此时的面积和为多少?
解:设一个正方形的边长为a cm,则另一个正方形的边长为
=(18-a)cm.则两个正方形的面积和为:
S=a2+(18-a)2=2a2-36a+324(0<x<18).
将上式进行配方得:S=2(a-9)2+162(0<x<18).
当a=9 cm时,S最小,最小值为162 cm2.此时,她将彩带二等分.
答:她应将彩带分成相等的两段剪,此时的面积和为162 cm2.
3、某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单位每涨1元,月销售量就减少10千克.
(1)设销售单价为每千克x元,月销售利润为y元,求y与x的函数表达式(不必写出x的取值范围);
(2)商店销售单价应定为多少、销售利润最大?
解:(1)可卖出千克数为500-10(x-50)=1000-10x,
y与x的函数表达式为y=(x-40)(1000-10x)
=-10x2+1400x-40000,
(2)当 时,y有最大值.
答:商店销售单价应定为70元时,销售利润最大.
用抛物线的知识解决生活中的一些实际问题一般步骤:
生活中的一些实际问题
弄清题中量与量之间的依赖关系
建立函数模型
利用二次函数图象和性质解决实际问题
注意自变量的取值范围
