第8讲 一元一次不等式(组)及其应用 课件(共26张PPT) 2025年中考数学一轮专题复习
文档属性
| 名称 | 第8讲 一元一次不等式(组)及其应用 课件(共26张PPT) 2025年中考数学一轮专题复习 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-07 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
第一部分 系统复习 成绩基石
第二章 方程(组)与不等式(组)
第8讲 一元一次不等式(组)及其应用
理考点·练基础
多维设问·练重难
聚焦河南·精练命题点
考点一 不等式的有关概念
不等式 用①________连接的式子叫做不等式.常用的不等号有:“ ”“
”“ ”“ ”“ ”
不等式的解 使不等式成立的②____________叫做这个不等式的解
不等式的解集 一个不等式的③________组成这个不等式的解集
解不等式 求不等式解集的过程,叫做解不等式
不等号
未知数的值
所有解
1.在下列数学表达式;;;; ;
中,是不等式的有__________.
2.在4,3,2,1,0,,中,能使不等式 成立的数有___个.
①②⑤⑥
2
考点二 不等式的性质
文字描述 式子表达
性质1 不等式的两边都加上(或减去)同一个数或 同一个整式,不等号的方向①______ 若,则 ___
性质2 不等式的两边都乘(或除以)同一个正数,不 等号的方向③______ 若,,则 ___
,___
性质3 不等式的两边都乘(或除以)同一个负数,不 等号的方向⑥______ 若,,则 ___
,___
系数化为1时,不等式两边同时乘或除以同一个负数,一定要改变不等
号的方向(不等式的性质3).
不变
不变
改变
3.若,,用“ ”或“ ”填空:
(1)___ ;
(2)___ ;
(3)___ ;
(4)___ ;
(5)___ ;
(6)___ .
考点三 一元一次不等式(组)及其解法(10年10考)
一元一次不等式 的概念 只含有①______未知数,并且未知数的次数是②___的不等式,叫
做一元一次不等式
解一元一次不等 式的一般步骤 (1)去分母;________;(3)移项;
____________;(5)系数化为1(系数化为1时,注意不等号方
向是否改变)
解一元一次不等 式组的一般步骤 先求出各不等式的解集,各不等式解集的⑤__________就是不等
式组的解集;可以借助于数轴来求解
一个
1
去括号
合并同类项
公共部分
4.解不等式: .
解:去分母,得 ,
移项,得 ,
合并同类项,得 ,
不等式的两边都除以,得 .
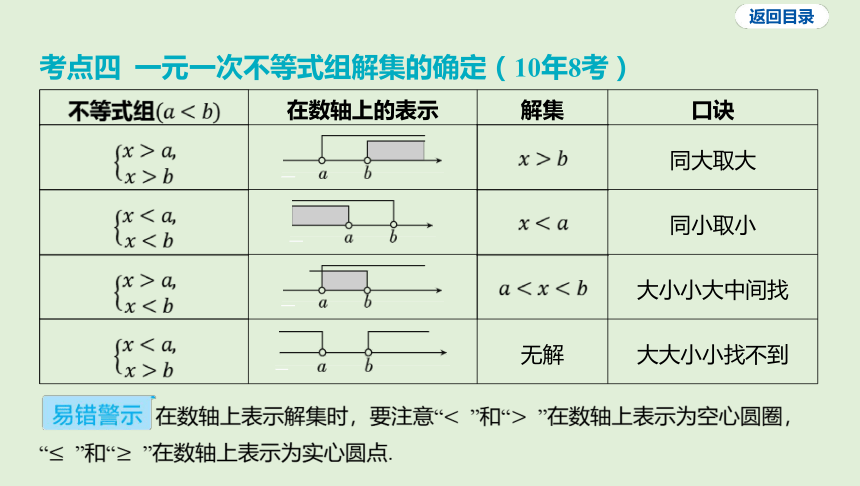
考点四 一元一次不等式组解集的确定(10年8考)
不等式组 在数轴上的表示 解集 口诀
_________________________________________ 同大取大
_____________________________________ 同小取小
_________________________________________ 大小小大中间找
____________________________________________ 无解 大大小小找不到
在数轴上表示解集时,要注意“ ”和“ ”在数轴上表示为空心圆圈,
“ ”和“ ”在数轴上表示为实心圆点.
5.解不等式组
,
请按下列步骤完成解答:
(1)解不等式①,得________;
(2)解不等式②,得________;
(3)将不等式①和②的解集在数轴表示出来;
[答案]
(4)原不等式组的解集为________.
考点五 一元一次不等式(组)的应用(10年9考)
1.列不等式解应用题的基本步骤:(1)审题;(2)设未知数;(3)列不等式;(4)解
不等式;(5)检验;(6)作答.
2.在实际问题中,常见的关键词与不等号的对应关系如下:
表示不等关系的常见关键词 不等号
大于,多于,超过,高于
小于,少于,不足,低于
至少,不低于,不小于,不少于 ①___
至多,不高于,不大于,不超过 ②___
6.某校组织知识竞赛,共有20道题.评分标准为:对1题给10分,错1题或不答都扣5
分.乐乐至少要答对几道题,总分才不会低于80分?
解:设乐乐答对 道题.
,解得 .
又 为正整数,
的最小值为12.
答:乐乐至少要答对12道题,总分才不会低于80分.
一元一次不等式(组)的实际应用
例 某品牌笔记本的成本为每台2 500元,售价为每台3 200元.
设问1: 某中学计划为新教师配备一批新笔记本电脑,要使购买的总费用不超过
30 000元.则最多可购进多少台电脑?
解:设可购进 台电脑.
,
解得 .
又为正整数, 的最大值为9.
答:最多购进9台电脑.
设问2: 该商店准备开展打折促销活动,要求利润率不低于成本的 ,则这种品牌的
笔记本电脑最多可以打几折销售.
解:设这种品牌的笔记本电脑可以打 折销售.
,
解得 .
答:这种品牌的笔记本电脑最多可以打8.75折.
设问3: 吴老师的女儿准备用自己节省的零花钱购买一台笔记本电脑,她已存有1 300
元,并计划从本月起每月节省180元,求至少需要多少个月后超过这台笔记本的费用.
解:设需要 个月后能超过这台笔记本的费用.
,
解得 .
为正整数, 的最小值为11.
答:至少需要11个月后超过这台笔记本的费用.
设问4: 某商店先把电脑的售价提高,然后在此基础上打8折售出,若新的电脑售价不
低于原电脑的售价,商店将电脑的售价至少提高了多少元?
解:设商店将电脑的售价提高了 元.
,解得 .
答:商店将电脑的售价至少提高了800元.
一元一次不等式(组)的解法及解集表示(10年10考)
1.(2024河南5题3分)下列不等式中,与 组成的不等式组无解的是( )
A
A. B. C. D.
2.(2018河南备用卷7题3分)不等式组 的解集在数轴上表示正确的是
( )
D
A. B. C. D.
3.(2022河南12题3分)不等式组 的解集为__________.
不等式组 的正整数解的和为____.
4.(2020河南12题3分)已知关于的不等式组其中, 在数轴上的对应点
如图所示,则这个不等式组的解集为_______.
10
若实数在数轴上的位置如图所示,则关于的不等式组 的
解集为______.
一元一次不等式(组)的应用(10年9考)
5.(2023河南21题9分)某健身器材专卖店推出两种优惠活动,并规定购物时只能
选择其中一种.
活动一:所购商品按原价打八折;
活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80
元,需付款220元;所购商品原价为770元,可减160元,需付款610元)
(1)购买一件原价为450元的健身器材时,选择哪种活动更合算?请说明理由;
解:活动一: (元),
活动二: (元),
, 选择活动一更合算.
(2)购买一件原价在500元以下的健身器材时,若选择活动一和选择活动二的付款
金额相等,求一件这种健身器材的原价;
解:设一件这种健身器材的原价为 元.
若 ,则活动一按原价打八折,活动二按原价,此时付款金额不可能相等.
,,解得 .
答:一件这种健身器材的原价是400元.
(3)购买一件原价在900元以下的健身器材时,原价在什么范围内,选择活动二比
选择活动一更合算?设一件这种健身器材的原价为元,请直接写出 的取值范围.
解:或 .
6.(2021河南21题9分)猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小
李在某网店选中, 两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价
和销售价如下表:
类别 价格 款玩偶 款玩偶
进货价(元/个) 40 30
销售价(元/个) 56 45
(1)第一次小李用1 100元购进了, 两款玩偶共30个,求两款玩偶各购进多少个;
解:设款玩偶购进个,则款玩偶购进 个.
由题意,得 ,
解得,则 .
答:款玩偶购进20个, 款玩偶购进10个.
(2)第二次小李进货时,网店规定款玩偶进货数量不得超过 款玩偶进货数量的
一半.小李计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最
大利润是多少?
解:设款玩偶购进个,款玩偶购进个,获利 元.
由题意,得 .
款玩偶进货数量不得超过款玩偶进货数量的一半,, .
,,随 的增大而增大,
当时, .
此时, .
答:按照款玩偶购进10个, 款玩偶购进20个的方案进货才能获得最大利润,最大
利润是460元.
(3)小李第二次进货时采取了(2)中设计的方案,并且两次购进的玩偶全部售出,
请从利润率的角度分析,对于小李来说哪一次更合算?(注:利润率
)
解:第一次的利润率为
,
第二次的利润率为 .
,
对于小李来说第二次的进货方案更合算.
7.(2024包头中考)若,, 这三个实数在数轴上所对应的点从左到
右依次排列,则 的取值范围是( )
B
A. B. C. D.
8.如图,若是整数,且满足则 落在( )
B
A.段④ B.段③ C.段② D.段①
9.(2024山东中考)根据以下对话,
给出下列三个结论:
班学生的最高身高为 ;
班学生的最低身高小于 ;
班学生的最高身高大于或等于 .
上述结论中,所有正确结论的序号是( )
C
A.①② B.①③ C.②③ D.①②③
[解析] 设1班同学的最高身高为,最低身高为 ,2班同学的最高身高为
,最低身高为,根据1班班长的对话,得, ,
,,解得 ,故③正确;根据2班班长的对
话,得,,,, ,
故②正确.
第一部分 系统复习 成绩基石
第二章 方程(组)与不等式(组)
第8讲 一元一次不等式(组)及其应用
理考点·练基础
多维设问·练重难
聚焦河南·精练命题点
考点一 不等式的有关概念
不等式 用①________连接的式子叫做不等式.常用的不等号有:“ ”“
”“ ”“ ”“ ”
不等式的解 使不等式成立的②____________叫做这个不等式的解
不等式的解集 一个不等式的③________组成这个不等式的解集
解不等式 求不等式解集的过程,叫做解不等式
不等号
未知数的值
所有解
1.在下列数学表达式;;;; ;
中,是不等式的有__________.
2.在4,3,2,1,0,,中,能使不等式 成立的数有___个.
①②⑤⑥
2
考点二 不等式的性质
文字描述 式子表达
性质1 不等式的两边都加上(或减去)同一个数或 同一个整式,不等号的方向①______ 若,则 ___
性质2 不等式的两边都乘(或除以)同一个正数,不 等号的方向③______ 若,,则 ___
,___
性质3 不等式的两边都乘(或除以)同一个负数,不 等号的方向⑥______ 若,,则 ___
,___
系数化为1时,不等式两边同时乘或除以同一个负数,一定要改变不等
号的方向(不等式的性质3).
不变
不变
改变
3.若,,用“ ”或“ ”填空:
(1)___ ;
(2)___ ;
(3)___ ;
(4)___ ;
(5)___ ;
(6)___ .
考点三 一元一次不等式(组)及其解法(10年10考)
一元一次不等式 的概念 只含有①______未知数,并且未知数的次数是②___的不等式,叫
做一元一次不等式
解一元一次不等 式的一般步骤 (1)去分母;________;(3)移项;
____________;(5)系数化为1(系数化为1时,注意不等号方
向是否改变)
解一元一次不等 式组的一般步骤 先求出各不等式的解集,各不等式解集的⑤__________就是不等
式组的解集;可以借助于数轴来求解
一个
1
去括号
合并同类项
公共部分
4.解不等式: .
解:去分母,得 ,
移项,得 ,
合并同类项,得 ,
不等式的两边都除以,得 .
考点四 一元一次不等式组解集的确定(10年8考)
不等式组 在数轴上的表示 解集 口诀
_________________________________________ 同大取大
_____________________________________ 同小取小
_________________________________________ 大小小大中间找
____________________________________________ 无解 大大小小找不到
在数轴上表示解集时,要注意“ ”和“ ”在数轴上表示为空心圆圈,
“ ”和“ ”在数轴上表示为实心圆点.
5.解不等式组
,
请按下列步骤完成解答:
(1)解不等式①,得________;
(2)解不等式②,得________;
(3)将不等式①和②的解集在数轴表示出来;
[答案]
(4)原不等式组的解集为________.
考点五 一元一次不等式(组)的应用(10年9考)
1.列不等式解应用题的基本步骤:(1)审题;(2)设未知数;(3)列不等式;(4)解
不等式;(5)检验;(6)作答.
2.在实际问题中,常见的关键词与不等号的对应关系如下:
表示不等关系的常见关键词 不等号
大于,多于,超过,高于
小于,少于,不足,低于
至少,不低于,不小于,不少于 ①___
至多,不高于,不大于,不超过 ②___
6.某校组织知识竞赛,共有20道题.评分标准为:对1题给10分,错1题或不答都扣5
分.乐乐至少要答对几道题,总分才不会低于80分?
解:设乐乐答对 道题.
,解得 .
又 为正整数,
的最小值为12.
答:乐乐至少要答对12道题,总分才不会低于80分.
一元一次不等式(组)的实际应用
例 某品牌笔记本的成本为每台2 500元,售价为每台3 200元.
设问1: 某中学计划为新教师配备一批新笔记本电脑,要使购买的总费用不超过
30 000元.则最多可购进多少台电脑?
解:设可购进 台电脑.
,
解得 .
又为正整数, 的最大值为9.
答:最多购进9台电脑.
设问2: 该商店准备开展打折促销活动,要求利润率不低于成本的 ,则这种品牌的
笔记本电脑最多可以打几折销售.
解:设这种品牌的笔记本电脑可以打 折销售.
,
解得 .
答:这种品牌的笔记本电脑最多可以打8.75折.
设问3: 吴老师的女儿准备用自己节省的零花钱购买一台笔记本电脑,她已存有1 300
元,并计划从本月起每月节省180元,求至少需要多少个月后超过这台笔记本的费用.
解:设需要 个月后能超过这台笔记本的费用.
,
解得 .
为正整数, 的最小值为11.
答:至少需要11个月后超过这台笔记本的费用.
设问4: 某商店先把电脑的售价提高,然后在此基础上打8折售出,若新的电脑售价不
低于原电脑的售价,商店将电脑的售价至少提高了多少元?
解:设商店将电脑的售价提高了 元.
,解得 .
答:商店将电脑的售价至少提高了800元.
一元一次不等式(组)的解法及解集表示(10年10考)
1.(2024河南5题3分)下列不等式中,与 组成的不等式组无解的是( )
A
A. B. C. D.
2.(2018河南备用卷7题3分)不等式组 的解集在数轴上表示正确的是
( )
D
A. B. C. D.
3.(2022河南12题3分)不等式组 的解集为__________.
不等式组 的正整数解的和为____.
4.(2020河南12题3分)已知关于的不等式组其中, 在数轴上的对应点
如图所示,则这个不等式组的解集为_______.
10
若实数在数轴上的位置如图所示,则关于的不等式组 的
解集为______.
一元一次不等式(组)的应用(10年9考)
5.(2023河南21题9分)某健身器材专卖店推出两种优惠活动,并规定购物时只能
选择其中一种.
活动一:所购商品按原价打八折;
活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80
元,需付款220元;所购商品原价为770元,可减160元,需付款610元)
(1)购买一件原价为450元的健身器材时,选择哪种活动更合算?请说明理由;
解:活动一: (元),
活动二: (元),
, 选择活动一更合算.
(2)购买一件原价在500元以下的健身器材时,若选择活动一和选择活动二的付款
金额相等,求一件这种健身器材的原价;
解:设一件这种健身器材的原价为 元.
若 ,则活动一按原价打八折,活动二按原价,此时付款金额不可能相等.
,,解得 .
答:一件这种健身器材的原价是400元.
(3)购买一件原价在900元以下的健身器材时,原价在什么范围内,选择活动二比
选择活动一更合算?设一件这种健身器材的原价为元,请直接写出 的取值范围.
解:或 .
6.(2021河南21题9分)猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小
李在某网店选中, 两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价
和销售价如下表:
类别 价格 款玩偶 款玩偶
进货价(元/个) 40 30
销售价(元/个) 56 45
(1)第一次小李用1 100元购进了, 两款玩偶共30个,求两款玩偶各购进多少个;
解:设款玩偶购进个,则款玩偶购进 个.
由题意,得 ,
解得,则 .
答:款玩偶购进20个, 款玩偶购进10个.
(2)第二次小李进货时,网店规定款玩偶进货数量不得超过 款玩偶进货数量的
一半.小李计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最
大利润是多少?
解:设款玩偶购进个,款玩偶购进个,获利 元.
由题意,得 .
款玩偶进货数量不得超过款玩偶进货数量的一半,, .
,,随 的增大而增大,
当时, .
此时, .
答:按照款玩偶购进10个, 款玩偶购进20个的方案进货才能获得最大利润,最大
利润是460元.
(3)小李第二次进货时采取了(2)中设计的方案,并且两次购进的玩偶全部售出,
请从利润率的角度分析,对于小李来说哪一次更合算?(注:利润率
)
解:第一次的利润率为
,
第二次的利润率为 .
,
对于小李来说第二次的进货方案更合算.
7.(2024包头中考)若,, 这三个实数在数轴上所对应的点从左到
右依次排列,则 的取值范围是( )
B
A. B. C. D.
8.如图,若是整数,且满足则 落在( )
B
A.段④ B.段③ C.段② D.段①
9.(2024山东中考)根据以下对话,
给出下列三个结论:
班学生的最高身高为 ;
班学生的最低身高小于 ;
班学生的最高身高大于或等于 .
上述结论中,所有正确结论的序号是( )
C
A.①② B.①③ C.②③ D.①②③
[解析] 设1班同学的最高身高为,最低身高为 ,2班同学的最高身高为
,最低身高为,根据1班班长的对话,得, ,
,,解得 ,故③正确;根据2班班长的对
话,得,,,, ,
故②正确.
同课章节目录
