第1讲 实数 课件(共27张PPT) 中考2025年数学一轮复习
文档属性
| 名称 | 第1讲 实数 课件(共27张PPT) 中考2025年数学一轮复习 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-07 14:42:37 | ||
图片预览








文档简介
(共27张PPT)
第一部分 系统复习 成绩基石
第一章 数与式
第1讲 实数
理考点·练基础
聚焦河南·精练命题点
考点一 实数的分类(10年1考)
1.常用正负数表示具有相反意义的量.
2.无理数的常见形式:①有规律的无限不循环小数,如 (两个1之间
依次多一个0)等;②最终结果含有 的数,如 ,等;③开方开不尽的数,如,等;
④某些三角函数值,如 , 等.
1.把下列各数填在相应的横线上.
,, ,
0,,,,2, ,
(每两个1之间逐次增加1个0)
(1)正数集合:{________________________________________________________
_________}
(2)负数集合:{_ ______________________________________}
,,2, (每两个1之间逐次增加1个))
,,,,
(3)整数集合:{____________}
(4)负分数集合:{_ _____________________________}
(5)无理数集合:{_ ____________________________________________________}
0,2,
,,…
, (每两个1之间逐次增加1个)
考点二 实数的相关概念(10年8考)
定义 性质
数轴 规定了①______、②________ 和③__________的直线 ④______与数轴上的点是一一对应的
相反数 只有⑤______不同的两个数互 为相反数 (1)非零实数 的相反数是⑥____.特别
地,0的相反数是⑦___;
(2),互为相反数 ;
(3)在数轴上,表示相反数的两个点位
于原点的两侧,且到原点的距离⑧______
原点
正方向
单位长度
实数
符号
0
相等
定义 性质
绝对值 数轴上表示数 的点到原点的 ⑨______,叫做数 的绝对值,记 作
倒数 乘积为1的两个数互为倒数 ,互为倒数 ;
(2)非零实数的倒数为 ,0没有倒数;
(3)倒数等于本身的数是
距离
续表
2.在如图所示的数轴上有,,,,, ,6个点.
(1)如图所示的数轴是一条单位长度为___的直线;
(2)表示的数字是互为相反数的点为_____________;
(3)若,则数字 对应数轴上的点为______;(填字母)
(4)数轴上点 表示的数的倒数为___.
1
和;和
或
2
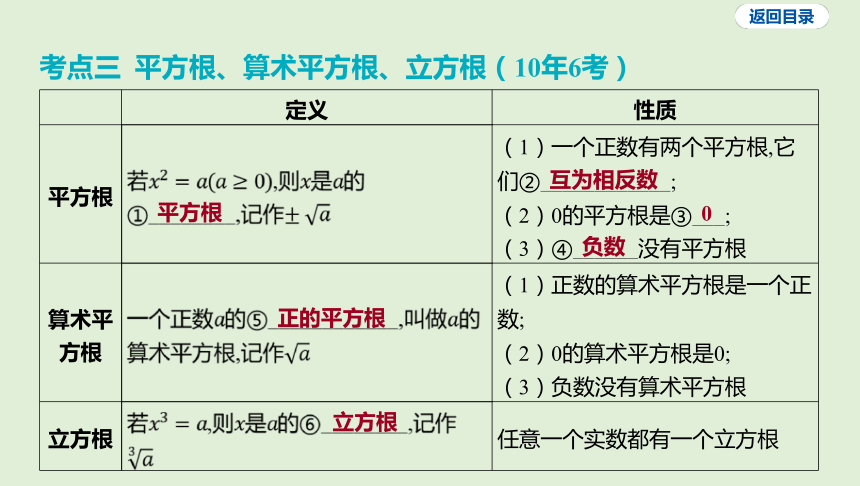
考点三 平方根、算术平方根、立方根(10年6考)
定义 性质
平方根 若,则是 的 ①________,记作 (1)一个正数有两个平方根,它
们②____________;
(2)0的平方根是③___;
(3)④______没有平方根
算术平 方根 一个正数的⑤____________,叫做 的 算术平方根,记作 (1)正数的算术平方根是一个正
数;
(2)0的算术平方根是0;
(3)负数没有算术平方根
立方根 若,则是 的⑥________,记作 任意一个实数都有一个立方根
平方根
互为相反数
0
负数
正的平方根
立方根
3.如果一个数的平方根是 ,那么这个数是____.
4.若,则 _______.
5.64的算术平方根是___.
6. 的立方根是___.
7.平方根等于本身的数为___;立方根等于本身的数为_______.
64
8或
8
2
0
,0
考点四 科学记数法、近似数(10年8考)
科学记数法 定义 把一个数表示成①________(其中, 是整数)
的形式
值 的确 定 当 原数的绝对值时,为负整数, 等于这个数左起
第一个非零数字前所有零的个数(包括小数点前的零)
当原数的绝对值时, 为自然数且等于这个数的整数位
数②_____
近似数 将一个数③__________后得到的数 精确度 一般地,一个近似数四舍五入到哪一位,就说这个近似数精确到 哪一位
减1
四舍五入
8.用科学记数法表示下列各数:
(1) ____________;
(2) ___________;
(3) _____________;
(4) ______________;
(5)361万 ____________.
9.用四舍五入法按要求对下列各数取近似值,并用科学记数法表示.
(1) (精确到百位);
解:(精确到百位) ;
(2)(精确到 );
解:(精确到) ;
(3) (精确到千位).
解:(精确到千位) .
考点五 实数的大小比较(10年3考)
数轴比较法 数轴上表示的两个数,右边的点表示的数总比左边的点表示的数
①____
类别比较法 正数②______0,负数③______0,正数④______一切负数;两个负数,
绝对值大的⑤________
差值比较法 ;;
平方比较法
在一组数据中,当求最大的数时,在正数中找;当求最小的数时,在
负数中找,注意两个负数比较大小时,绝对值大的反而小.
大
大于
小于
大于
反而小
10.比较大小:
(1)2___ ;
(2)___ ;
(3)___ ;
(4)已知有理数在数轴上的位置如图所示,则___1.(填“ ”“ ”或“ ”)
考点六 实数的运算(10年9考)
零次幂和 负整数指 数幂 零次幂: ;
负整数指数幂:(, 为正整数)
非负数 常见的三类非负数:①绝对值,即 ;②偶次方数
(常见是平方数),即( 是正整数);③算术平方根,即
四则运算 加法 (1)同号两数相加,取相同的符号,并把绝对值相加;
(2)异号两数相加,绝对值相等时和为0;绝对值不相等
时,取绝对值较大的数的符号,并用较大的绝对值①______
较小的绝对值;
(3)一个数同②___相加,仍得这个数
减法 减去一个数,等于加上这个数的相反数,即
乘法 两数相乘,同号得正,异号得负,并把绝对值相乘.任何数与
0相乘,都得0
除法 除以一个不为0的数等于乘这个数的③______
减去
0
倒数
续表
运算顺序 (1)先算④____________,再算⑤______,最后算⑥______;
(2)同级运算,按照⑦__________的顺序依次计算;
(3)如有括号,先算小括号里面的,再算中括号里面的,最后算大括号
里面的
乘方、开方
乘除
加减
从左到右
续表
11.计算:
(1) ;
解:原式 .
(2) ;
解:原式
.
(3) .
解:原式 .
实数的分类(10年1考)
1.开放性设问 (2020河南11题3分)请写出一个大于1且小于2的无理数__________
_________.
请写出一个整数部分为1的无理数__________________.
(答案不唯一)
(答案不唯一)
实数的相关概念(10年8考)
2.(2022河南1题3分) 的相反数是( )
A
A. B.2 C. D.
的相反数是( )
B
A. B. C. D.
3.(2021河南1题3分) 的绝对值是( )
A
A.2 B. C. D.
反向设问 绝对值为 的数是( )
D
A.5 B. C. D.
科学记数法(10年6考)
4.(2023河南3题3分)2022年河南省出版的4.59亿册图书,为贯彻落实党的二十大
关于深化全民阅读活动的重要精神,建设学习型社会提供了丰富的图书资源.数据
“4.59亿”用科学记数法表示为( )
C
A. B. C. D.
党的二十大报告指出:十年来,我国建成了世界上规模最大的教育体
系、社会保障体系、医疗卫生体系,教育普及水平实现了历史性跨越,基本养老保
险覆盖了十亿四千万人,基本医疗保险参保率稳定在百分之九十五.数据“十亿四千
万”用科学记数法表示为( )
C
A. B. C. D.
5.(2019河南2题3分)成人每天维生素D的摄入量约为 克.数据“
”用科学记数法表示为( )
C
A. B. C. D.
变设问 “白日不到处,青春恰自来.苔花如米小,也学牡丹开.”这是清
朝袁枚所写五言绝句《苔》,这首咏物诗启示我们身处逆境也要努力绽放自己,要
和苔花一样尽自己所能实现人生价值.苔花也被称为“坚韧之花”.袁枚所写的“苔花”
很可能是苔类孢子体的孢蒴,某孢子体的孢蒴直径约为 ,将数据
用科学记数法表示为,则 的值是( )
D
A.6 B. C. D.
实数的大小比较(10年3考)
6.(2023河南1题3分)下列各数中最小的数是( )
A
A. B.0 C.1 D.
7.(2017河南1题3分)下列各数中比1大的数是( )
A
A.2 B.0 C. D.
实数的运算(10年9考)
8.计算:
(1)(2023河南16题(1)5分)计算: ;
解:原式 .
(2)(2022河南16题(1)5分) ;
解:原式 .
(3)(2021河南16题(1)5分) .
解:原式 .
9.新情境·信息技术 (2024威海中考)据央视网2023年10月11日消息,中国科学技
术大学中国科学院量子创新研究院与上海微系统所、国家并行计算机工程技术研究
中心合作,成功构建了255个光子的量子计算原型机“九章三号”,再度刷新了光量
子信息的技术水平和量子计算优越性的世界纪录.“九章三号”处理高斯玻色取样的
速度比上一代“九章二号”提升一
百万倍,在百万分之一秒时间内所处理的最高复杂度的样本,需要当前最强的超级
计算机花费超过二百亿年的时间.将“百万分之一”用科学记数法表示为( )
B
A. B. C. D.
10.(2024台湾中考)如图的数在线有,, 三点.今打算在此数在线
标示,两点,且,互为倒数,若在 的左侧,则下列叙述何者正确
( )
B
A.在上,且 B.在上,且
C.在上,且 D.在上,且
11.数学文化 (2024陕西中考)小华探究“幻方”时,提出了一个问题:
如图,将0,, ,1,2这五个数分别填在五个小正方形内,使
横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方
形内的数可以是___.(写出一个符合题意的数即可)
0
第一部分 系统复习 成绩基石
第一章 数与式
第1讲 实数
理考点·练基础
聚焦河南·精练命题点
考点一 实数的分类(10年1考)
1.常用正负数表示具有相反意义的量.
2.无理数的常见形式:①有规律的无限不循环小数,如 (两个1之间
依次多一个0)等;②最终结果含有 的数,如 ,等;③开方开不尽的数,如,等;
④某些三角函数值,如 , 等.
1.把下列各数填在相应的横线上.
,, ,
0,,,,2, ,
(每两个1之间逐次增加1个0)
(1)正数集合:{________________________________________________________
_________}
(2)负数集合:{_ ______________________________________}
,,2, (每两个1之间逐次增加1个))
,,,,
(3)整数集合:{____________}
(4)负分数集合:{_ _____________________________}
(5)无理数集合:{_ ____________________________________________________}
0,2,
,,…
, (每两个1之间逐次增加1个)
考点二 实数的相关概念(10年8考)
定义 性质
数轴 规定了①______、②________ 和③__________的直线 ④______与数轴上的点是一一对应的
相反数 只有⑤______不同的两个数互 为相反数 (1)非零实数 的相反数是⑥____.特别
地,0的相反数是⑦___;
(2),互为相反数 ;
(3)在数轴上,表示相反数的两个点位
于原点的两侧,且到原点的距离⑧______
原点
正方向
单位长度
实数
符号
0
相等
定义 性质
绝对值 数轴上表示数 的点到原点的 ⑨______,叫做数 的绝对值,记 作
倒数 乘积为1的两个数互为倒数 ,互为倒数 ;
(2)非零实数的倒数为 ,0没有倒数;
(3)倒数等于本身的数是
距离
续表
2.在如图所示的数轴上有,,,,, ,6个点.
(1)如图所示的数轴是一条单位长度为___的直线;
(2)表示的数字是互为相反数的点为_____________;
(3)若,则数字 对应数轴上的点为______;(填字母)
(4)数轴上点 表示的数的倒数为___.
1
和;和
或
2
考点三 平方根、算术平方根、立方根(10年6考)
定义 性质
平方根 若,则是 的 ①________,记作 (1)一个正数有两个平方根,它
们②____________;
(2)0的平方根是③___;
(3)④______没有平方根
算术平 方根 一个正数的⑤____________,叫做 的 算术平方根,记作 (1)正数的算术平方根是一个正
数;
(2)0的算术平方根是0;
(3)负数没有算术平方根
立方根 若,则是 的⑥________,记作 任意一个实数都有一个立方根
平方根
互为相反数
0
负数
正的平方根
立方根
3.如果一个数的平方根是 ,那么这个数是____.
4.若,则 _______.
5.64的算术平方根是___.
6. 的立方根是___.
7.平方根等于本身的数为___;立方根等于本身的数为_______.
64
8或
8
2
0
,0
考点四 科学记数法、近似数(10年8考)
科学记数法 定义 把一个数表示成①________(其中, 是整数)
的形式
值 的确 定 当 原数的绝对值时,为负整数, 等于这个数左起
第一个非零数字前所有零的个数(包括小数点前的零)
当原数的绝对值时, 为自然数且等于这个数的整数位
数②_____
近似数 将一个数③__________后得到的数 精确度 一般地,一个近似数四舍五入到哪一位,就说这个近似数精确到 哪一位
减1
四舍五入
8.用科学记数法表示下列各数:
(1) ____________;
(2) ___________;
(3) _____________;
(4) ______________;
(5)361万 ____________.
9.用四舍五入法按要求对下列各数取近似值,并用科学记数法表示.
(1) (精确到百位);
解:(精确到百位) ;
(2)(精确到 );
解:(精确到) ;
(3) (精确到千位).
解:(精确到千位) .
考点五 实数的大小比较(10年3考)
数轴比较法 数轴上表示的两个数,右边的点表示的数总比左边的点表示的数
①____
类别比较法 正数②______0,负数③______0,正数④______一切负数;两个负数,
绝对值大的⑤________
差值比较法 ;;
平方比较法
在一组数据中,当求最大的数时,在正数中找;当求最小的数时,在
负数中找,注意两个负数比较大小时,绝对值大的反而小.
大
大于
小于
大于
反而小
10.比较大小:
(1)2___ ;
(2)___ ;
(3)___ ;
(4)已知有理数在数轴上的位置如图所示,则___1.(填“ ”“ ”或“ ”)
考点六 实数的运算(10年9考)
零次幂和 负整数指 数幂 零次幂: ;
负整数指数幂:(, 为正整数)
非负数 常见的三类非负数:①绝对值,即 ;②偶次方数
(常见是平方数),即( 是正整数);③算术平方根,即
四则运算 加法 (1)同号两数相加,取相同的符号,并把绝对值相加;
(2)异号两数相加,绝对值相等时和为0;绝对值不相等
时,取绝对值较大的数的符号,并用较大的绝对值①______
较小的绝对值;
(3)一个数同②___相加,仍得这个数
减法 减去一个数,等于加上这个数的相反数,即
乘法 两数相乘,同号得正,异号得负,并把绝对值相乘.任何数与
0相乘,都得0
除法 除以一个不为0的数等于乘这个数的③______
减去
0
倒数
续表
运算顺序 (1)先算④____________,再算⑤______,最后算⑥______;
(2)同级运算,按照⑦__________的顺序依次计算;
(3)如有括号,先算小括号里面的,再算中括号里面的,最后算大括号
里面的
乘方、开方
乘除
加减
从左到右
续表
11.计算:
(1) ;
解:原式 .
(2) ;
解:原式
.
(3) .
解:原式 .
实数的分类(10年1考)
1.开放性设问 (2020河南11题3分)请写出一个大于1且小于2的无理数__________
_________.
请写出一个整数部分为1的无理数__________________.
(答案不唯一)
(答案不唯一)
实数的相关概念(10年8考)
2.(2022河南1题3分) 的相反数是( )
A
A. B.2 C. D.
的相反数是( )
B
A. B. C. D.
3.(2021河南1题3分) 的绝对值是( )
A
A.2 B. C. D.
反向设问 绝对值为 的数是( )
D
A.5 B. C. D.
科学记数法(10年6考)
4.(2023河南3题3分)2022年河南省出版的4.59亿册图书,为贯彻落实党的二十大
关于深化全民阅读活动的重要精神,建设学习型社会提供了丰富的图书资源.数据
“4.59亿”用科学记数法表示为( )
C
A. B. C. D.
党的二十大报告指出:十年来,我国建成了世界上规模最大的教育体
系、社会保障体系、医疗卫生体系,教育普及水平实现了历史性跨越,基本养老保
险覆盖了十亿四千万人,基本医疗保险参保率稳定在百分之九十五.数据“十亿四千
万”用科学记数法表示为( )
C
A. B. C. D.
5.(2019河南2题3分)成人每天维生素D的摄入量约为 克.数据“
”用科学记数法表示为( )
C
A. B. C. D.
变设问 “白日不到处,青春恰自来.苔花如米小,也学牡丹开.”这是清
朝袁枚所写五言绝句《苔》,这首咏物诗启示我们身处逆境也要努力绽放自己,要
和苔花一样尽自己所能实现人生价值.苔花也被称为“坚韧之花”.袁枚所写的“苔花”
很可能是苔类孢子体的孢蒴,某孢子体的孢蒴直径约为 ,将数据
用科学记数法表示为,则 的值是( )
D
A.6 B. C. D.
实数的大小比较(10年3考)
6.(2023河南1题3分)下列各数中最小的数是( )
A
A. B.0 C.1 D.
7.(2017河南1题3分)下列各数中比1大的数是( )
A
A.2 B.0 C. D.
实数的运算(10年9考)
8.计算:
(1)(2023河南16题(1)5分)计算: ;
解:原式 .
(2)(2022河南16题(1)5分) ;
解:原式 .
(3)(2021河南16题(1)5分) .
解:原式 .
9.新情境·信息技术 (2024威海中考)据央视网2023年10月11日消息,中国科学技
术大学中国科学院量子创新研究院与上海微系统所、国家并行计算机工程技术研究
中心合作,成功构建了255个光子的量子计算原型机“九章三号”,再度刷新了光量
子信息的技术水平和量子计算优越性的世界纪录.“九章三号”处理高斯玻色取样的
速度比上一代“九章二号”提升一
百万倍,在百万分之一秒时间内所处理的最高复杂度的样本,需要当前最强的超级
计算机花费超过二百亿年的时间.将“百万分之一”用科学记数法表示为( )
B
A. B. C. D.
10.(2024台湾中考)如图的数在线有,, 三点.今打算在此数在线
标示,两点,且,互为倒数,若在 的左侧,则下列叙述何者正确
( )
B
A.在上,且 B.在上,且
C.在上,且 D.在上,且
11.数学文化 (2024陕西中考)小华探究“幻方”时,提出了一个问题:
如图,将0,, ,1,2这五个数分别填在五个小正方形内,使
横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方
形内的数可以是___.(写出一个符合题意的数即可)
0
同课章节目录
