北师大版七年级数学下册第二章相交线与平行线本章总结提升课件(共24张PPT)
文档属性
| 名称 | 北师大版七年级数学下册第二章相交线与平行线本章总结提升课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 488.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-11 11:11:09 | ||
图片预览







文档简介
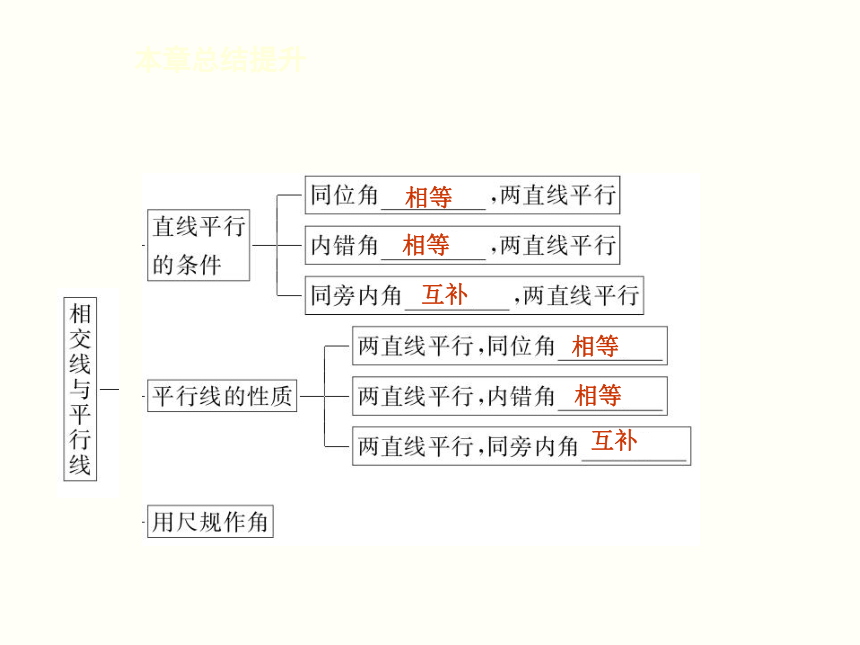
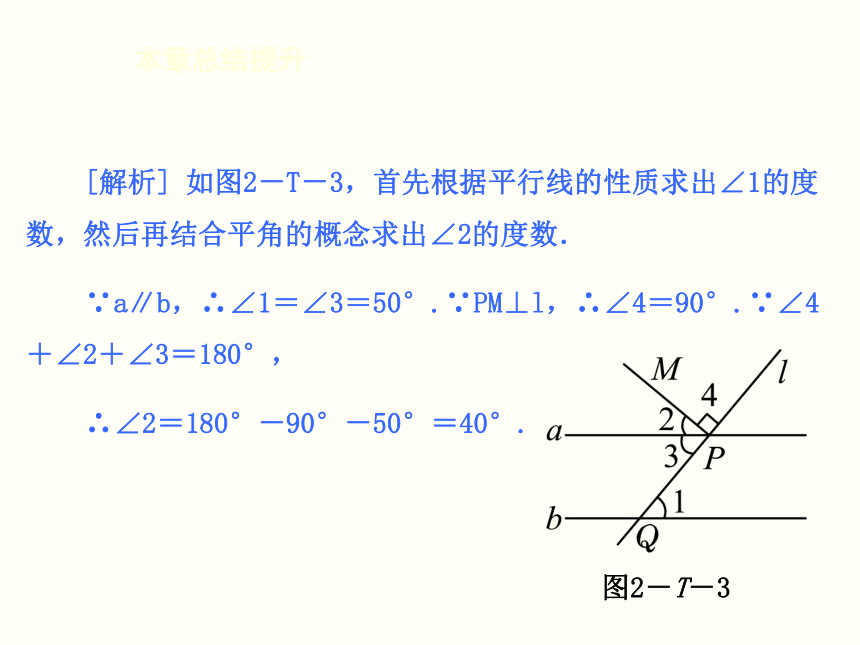
课件24张PPT。第二章 相交线与平行线本 章 总 结 提 升 本章知识框架本章总结提升90°(或直角) 180°(或平角) 相等 相等 相等 本章总结提升相等 相等 互补 相等 相等 互补 整合拓展创新本章总结提升? 类型之一 与相交线有关角(对顶角、互余、互补、垂直)的计算 例1 如图2-T-1,直线BC,DE交于O点,OA,OF为射线,AO⊥OB,OF平分∠COE,∠COF+∠BOD=51°.求∠AOD的度数. 图2-T-1本章总结提升[解析] 欲求∠AOD的度数,由于∠AOB=90°,所以关键是求∠BOD.由图可知∠BOD与∠EOC为对顶角,又OF平分∠COE,故∠BOD=2∠COF,再结合∠COF+∠BOD=51°可求解∠BOD.本章总结提升本章总结提升[点析] 两条直线相交,可能产生对顶角、互余、互补、垂直等,这些角并不是孤立存在的,它通常与其它角之间存在一定的位置关系和数量关系,本题中通过相关角之间的数量关系构建方程求解问题,解题关键是要善于挖掘图形中的隐含条件,综合运用所学知识,融会贯通,逐步分析与解决.本章总结提升? 类型二 与平行线性质、判定有关的计算与说理题 例2 [2014·沈阳] 如图2-T-2,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=50°,则∠2=________. 图2-T-2[答案] 40°本章总结提升[解析] 如图2-T-3,首先根据平行线的性质求出∠1的度数,然后再结合平角的概念求出∠2的度数.
∵a∥b,∴∠1=∠3=50°.∵PM⊥l,∴∠4=90°.∵∠4+∠2+∠3=180°,
∴∠2=180°-90°-50°=40°.图2-T-3 本章总结提升[点析]平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.反过来可得平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行. 本章总结提升例3 如图2-T-3所示,∠1=∠C,∠2=∠4,FG⊥BC于点G.
(1)∠2与∠3是否相等?试判断并说明理由.
(2)AD与BC是否互相垂直?试判断并说明理由.图2-T-3本章总结提升[解析] (1)由平行线的性质结合∠1=∠C可知∠2=∠3;(2)由(1)的结论及已知∠2=∠4即可判定AD∥FG,进而可得出AD与BC的垂直关系.本章总结提升解:(1)∠2=∠3.理由如下:
因为∠1=∠C,
所以ED∥AC,所以∠2=∠3.
(2)AD⊥BC.理由如下:
由(1)知∠2=∠3.
又因为∠2=∠4,所以∠3=∠4.
所以AD∥FG.
因为FG⊥BC,所以AD⊥BC.本章总结提升[点析] 借助垂直关系构建相关角之间的关系,进而得到两线平行,平行线的性质是指由两条直线的平行推出角之间关系.解题关键是综合运用了平行线的性质和判定,对条件进行单个分析或综合分析,对结论进行转化,有利于帮助我们转化角或找到角与角之间的关系,也有利于我们确定两条直线的位置关系.这是解决几何问题甚至是数学问题,找寻思路的常用方法.本章总结提升? 类型三 平行线知识的简单应用 例4 一条公路两次转弯后又回到原来的方向(即AB∥CD,如图2-T-5所示),如果第一次转弯时的∠B=140°,那么∠C应是( )
A.140° B.40°
C.100° D.180°
图2-T-5本章总结提升[解析] A 因为∠C与∠B是内错角,又因为AB∥CD,故∠C=∠B=140°,故选A.[点析] 这是平行线性质的简单应用.这类题的设计情境较新颖,主要考查运用数学知识解决实际问题的能力,体现了数学与生活的密切联系.本章总结提升? 类型四 尺规作图 例5 如图2-T-6所示,已知∠β,求作∠AOB,使∠AOB=2∠β. 图2-T-6本章总结提升解: 作法:(1)作射线OA;
(2)以射线OA为一边作∠AOC=∠β;
(3)以O为顶点,以射线OC为一边,在∠AOC的外部作∠BOC=∠β.则∠AOB就是所求作的角.如图2-T-7所示.图2-T-7 本章总结提升[点析]本题中两次运用基本作图——作一个角等于已知角.若继续以OB边在外部作∠BOD=∠β,可得∠AOD=3∠β..本章总结提升[点析]本题中两次运用基本作图——作一个角等于已知角.若继续以OB边在外部作∠BOD=∠β,可得∠AOD=3∠β..本章总结提升? 类型五 分类讨论思想 例6 已知∠AOC=90°,∠AOC∶∠AOB=3∶2,求∠BOC的度数. [解析] ∠AOB可能在∠AOC的外部,也可能在∠AOC的内部,需分类讨论.本章总结提升解:如图2-T-8所示.
因为∠AOC=90°,∠AOC∶∠AOB=3∶2,
所以∠AOB=60°.
当∠AOB在∠AOC的内部时(如图2-T-8①所示),
∠BOC=∠AOC-∠AOB=90°-60°=30°;
当∠AOB在∠AOC的外部时(如图2-T-8②所示),
∠BOC=∠AOC+∠AOB=90°+60°=150°.
所以∠BOC的度数为30°或150°.本章总结提升图2-T-8本章总结提升[点析]分类讨论思想是指被研究的问题包含多种可能情况,而又不能一概而论时,必须按可能出现的所有情况来分别讨论,得出各种情况下相应的结论,要遵循的规则是不重复、不遗漏任何一种可能的情况,每种可能情况都要按照同一标准进行讨论.
∵a∥b,∴∠1=∠3=50°.∵PM⊥l,∴∠4=90°.∵∠4+∠2+∠3=180°,
∴∠2=180°-90°-50°=40°.图2-T-3 本章总结提升[点析]平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.反过来可得平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行. 本章总结提升例3 如图2-T-3所示,∠1=∠C,∠2=∠4,FG⊥BC于点G.
(1)∠2与∠3是否相等?试判断并说明理由.
(2)AD与BC是否互相垂直?试判断并说明理由.图2-T-3本章总结提升[解析] (1)由平行线的性质结合∠1=∠C可知∠2=∠3;(2)由(1)的结论及已知∠2=∠4即可判定AD∥FG,进而可得出AD与BC的垂直关系.本章总结提升解:(1)∠2=∠3.理由如下:
因为∠1=∠C,
所以ED∥AC,所以∠2=∠3.
(2)AD⊥BC.理由如下:
由(1)知∠2=∠3.
又因为∠2=∠4,所以∠3=∠4.
所以AD∥FG.
因为FG⊥BC,所以AD⊥BC.本章总结提升[点析] 借助垂直关系构建相关角之间的关系,进而得到两线平行,平行线的性质是指由两条直线的平行推出角之间关系.解题关键是综合运用了平行线的性质和判定,对条件进行单个分析或综合分析,对结论进行转化,有利于帮助我们转化角或找到角与角之间的关系,也有利于我们确定两条直线的位置关系.这是解决几何问题甚至是数学问题,找寻思路的常用方法.本章总结提升? 类型三 平行线知识的简单应用 例4 一条公路两次转弯后又回到原来的方向(即AB∥CD,如图2-T-5所示),如果第一次转弯时的∠B=140°,那么∠C应是( )
A.140° B.40°
C.100° D.180°
图2-T-5本章总结提升[解析] A 因为∠C与∠B是内错角,又因为AB∥CD,故∠C=∠B=140°,故选A.[点析] 这是平行线性质的简单应用.这类题的设计情境较新颖,主要考查运用数学知识解决实际问题的能力,体现了数学与生活的密切联系.本章总结提升? 类型四 尺规作图 例5 如图2-T-6所示,已知∠β,求作∠AOB,使∠AOB=2∠β. 图2-T-6本章总结提升解: 作法:(1)作射线OA;
(2)以射线OA为一边作∠AOC=∠β;
(3)以O为顶点,以射线OC为一边,在∠AOC的外部作∠BOC=∠β.则∠AOB就是所求作的角.如图2-T-7所示.图2-T-7 本章总结提升[点析]本题中两次运用基本作图——作一个角等于已知角.若继续以OB边在外部作∠BOD=∠β,可得∠AOD=3∠β..本章总结提升[点析]本题中两次运用基本作图——作一个角等于已知角.若继续以OB边在外部作∠BOD=∠β,可得∠AOD=3∠β..本章总结提升? 类型五 分类讨论思想 例6 已知∠AOC=90°,∠AOC∶∠AOB=3∶2,求∠BOC的度数. [解析] ∠AOB可能在∠AOC的外部,也可能在∠AOC的内部,需分类讨论.本章总结提升解:如图2-T-8所示.
因为∠AOC=90°,∠AOC∶∠AOB=3∶2,
所以∠AOB=60°.
当∠AOB在∠AOC的内部时(如图2-T-8①所示),
∠BOC=∠AOC-∠AOB=90°-60°=30°;
当∠AOB在∠AOC的外部时(如图2-T-8②所示),
∠BOC=∠AOC+∠AOB=90°+60°=150°.
所以∠BOC的度数为30°或150°.本章总结提升图2-T-8本章总结提升[点析]分类讨论思想是指被研究的问题包含多种可能情况,而又不能一概而论时,必须按可能出现的所有情况来分别讨论,得出各种情况下相应的结论,要遵循的规则是不重复、不遗漏任何一种可能的情况,每种可能情况都要按照同一标准进行讨论.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
