北师大版七年级数学下册第四章三角形本章总结提升课件(共41张PPT)
文档属性
| 名称 | 北师大版七年级数学下册第四章三角形本章总结提升课件(共41张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 597.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-11 11:34:22 | ||
图片预览










文档简介
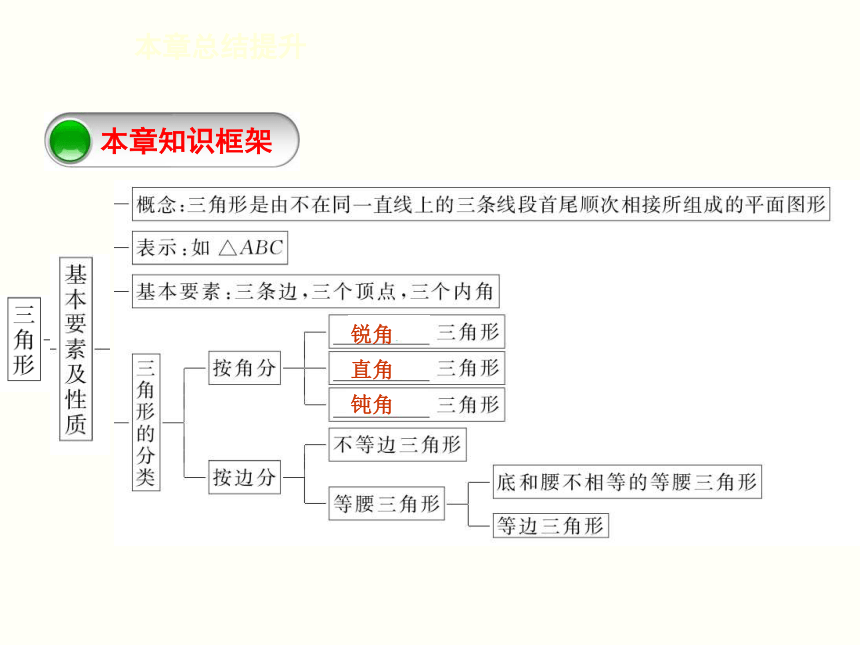
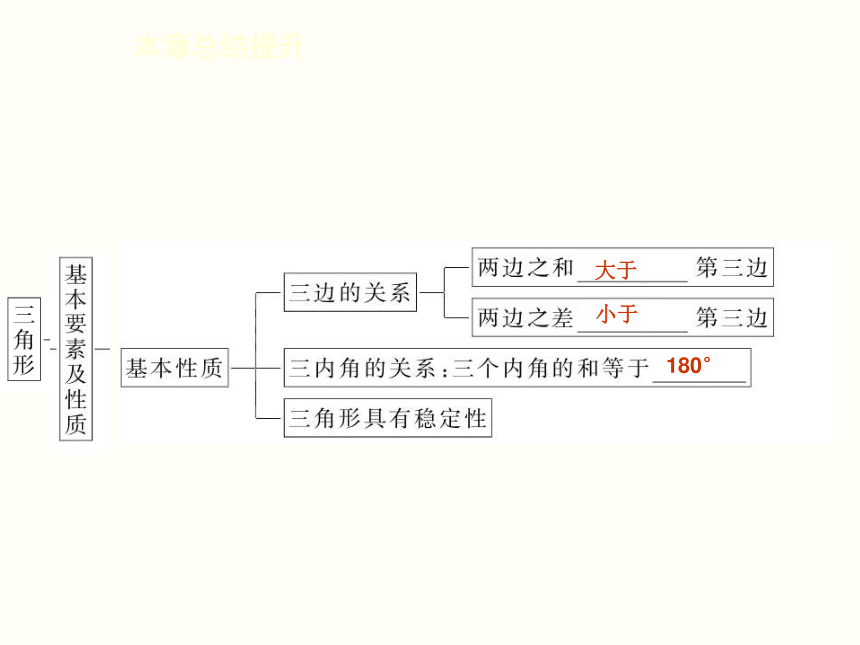
课件41张PPT。第四章 三角形本 章 总 结 提 升 本章知识框架本章总结提升锐角 直角 钝角 本章总结提升三 内 三 内 三 锐角 直角 钝角 本章总结提升大于 小于 180° 本章总结提升相等 相等 相等 相等 SSS SAS ASA AAS 整合拓展创新本章总结提升? 类型之一 与三角形的边有关的计算与说理 例1 已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.5 B.6 C.11 D.16[解析] C 已知三角形两边的长分别是4和10,所以第三边x的范围是6<x<14,在这个范围内,只有11符合.故选C.本章总结提升[点析] 已知三角形的两条边长,求第三边,根据“三角形两边之和大于第三边”和“三角形两边之差小于第三边”,可得“三角形的第三边大于两边之差且小于两边之和”,从而先求出第三边的范围,然后作出选择.本章总结提升例2 王伟准备用一段长30米的篱笆围成一个三角形形状的养兔圈,用于饲养家兔.已知第一条边长为a米,由于受地势限制,第二条边长只能比第一条边长的2倍多2米.
(1)请用a表示第三条边长;
(2)问第一条边长可以为8米吗?为什么?请说明理由;
(3)能否使得围成的养兔圈是等腰三角形?若能,说明你的围法;若不能,请说明理由.本章总结提升本章总结提升本章总结提升[点析]本题以构成三角形三边关系为载体,主要考查了整式计算与三角形的有关边知识的理解与运用,在探究等腰三角形的形状时要注意分类讨论,构建方程分析与解决实际问题.本章总结提升? 类型二 等腰三角形 例3 一个三角形的两条边相等,周长为18 cm,三角形一边长为4 cm,求其他两边长. [解析] 本题分两种情况:①腰长为4 cm,②底边长为4 cm.解答时要注意求出的边长要符合“三角形两边之和大于第三边”.本章总结提升本章总结提升[点析]等腰三角形是一种特殊而又十分重要的三角形,就是因为这种特殊性,在具体处理问题时往往又会出现错误,因此,同学们在求解有关等腰三角形的问题时一定要注意分类讨论.对于底和腰不等的等腰三角形,若条件中没有明确是底或腰时,应在符合三角形三边关系的前提下分类讨论. 本章总结提升? 类型三 与三角形的角有关的计算 例4 如图4-T-1,一个大型模板的设计要求是模板的BA边和CD边相交成50°角,DA边和CB边相交成30°角,如果通过测量∠A,∠B,∠C,∠D的度数来判断模板是否合格,你认为当∠D与∠B的度数相差多少时,模板刚好合格?图4-T-1本章总结提升[解析] 要判断∠D与∠B的度数相差多少时,模板刚好合格,可延长CD与BA,DA与CB,构造三角形,然后根据三角形内角和等于180°进行探究.解:当模板合格时,如图4-T-1,延长BA交CD的延长线于点E,则∠E=50°;延长DA交CB的延长线于点F,则∠F=30°,
由三角形的三个内角和等于180°,得
∠CBE+∠C+∠E=180°,∠CDF+∠C+∠F=180°,
所以∠CBE=180°-(∠E+∠C)=180°-(50°+∠C)=130°-∠C,本章总结提升∠CDF=180°-(∠F+∠C)=180°-(30°+∠C)=150°-∠C.
因为∠CDF-∠CBE=150°-∠C-(130°-∠C)=20°,
所以∠CDF比∠CBE大20°.
即∠D比∠B大20°时,模板刚好合格.
本章总结提升[点析]三角形的内角和等于180°,我们可以利用这一结论解决与角度计算有关的实际问题,解决问题的关键是如何将实际问题转化为数学问题.本章总结提升? 类型四 三角形中的重要线段例5 如图4-T-2,已知∠B=45°,∠C=75°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数. 图4-T-2本章总结提升本章总结提升本章总结提升图4-T-3[答案] 2本章总结提升本章总结提升[点析]解决本题的关键是利用三角形的面积关系,在高不变的情况下,底为中点或三等分点构成的三角形与原三角形的面积之间的关系,就是底之间的关系,注意数形结合及转换的数学思想方法. 本章总结提升? 类型五 尺规作图 例7 已知:线段a,c和∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.图4-T-4本章总结提升 解:如图4-T-5所示.①先画射线BC;图4-T-5本章总结提升②以∠α的顶点为圆心,任意长为半径画孤,分别交∠α的两边于A′,C′;
③以相同长度为半径,B为圆心,画弧,交BC于点F,以F为圆心,C′A′长为半径画弧,交已画弧于点E,连接EB,则∠EBF=∠α;
④在BF上取点C,使CB=a,以B为圆心,c为半径画圆交BE的延长线于点A,连接AC.△ABC即为所求作三角形.本章总结提升? 类型六 全等三角形中的开放性问题 例8 如图4-T-6所示,AB,CD相交于点O,AB=CD,试添加一个条件使得△AOD≌△COB,你添加的条件是__________(只需写一个).图4-T-6[答案] OA=OC或OB=OD本章总结提升[解析] 两个三角形全等的条件有“SAS”,“ASA”,“AAS”,“SSS”.结合题设中的已知,选择恰当的三角形全等条件是解决此类问题的关键.已知条件有AB=CD,隐含条件有∠AOD=∠COB,可选择“SAS”,填OA=OC或OB=OD.本章总结提升[点析]全等三角形是初中数学中最基础、最重要的一部分内容,本题是添加条件写结论的全开放型的创新题,这种类型的题目开放程度非常高,能激起同学们的挑战欲望和创新热情,实属好题. 本章总结提升? 类型七 全等三角形的性质与判定的综合应用 例9 如图4-T-7,已知点B,F,C,E在一条直线上,FB=CE,AC=DF.
能否由上面的已知条件说明AB∥ED?如果能,请给出说明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并说明理由.
供选择的三个条件(请从其中选择一个):
①AB=ED;②BC=EF; ③∠ACB=∠DFE.本章总结提升图4-T-7本章总结提升[解析] 由条件可知两三角形中具备了两边对应相等,可补充边借助“边边边”定理突破,也可补充这两边的夹角,借助“边角边”定理进行分析.解:由上面两条件不能说明AB∥ED.
有两种添加方法.
第一种:添加①AB=ED.
理由:因为FB=CE,所以BC=EF.本章总结提升又AC=DF,AB=ED,
所以△ABC≌△DEF.
所以∠B=∠E,
所以AB∥ED.
第二种:添加③∠ACB=∠DFE.
理由:因为FB=CE,
所以BC=EF.本章总结提升又∠ACB=∠DFE,AC=DF,
所以△ABC≌△DEF.
所以∠B=∠E,所以AB∥ED.[点析]近几年的各地中考中,全等三角形常以开放探究的形式出现,可能设置的问题结论不唯一,或条件不完备,即需要解题者依据题意确定结论或补全条件,或通过变换操作,或有关图形的动态变化导致某些图形、情境的变化,进而构建不同的数学模型,或选择不同的解题策略进行解答.本章总结提升例10 如图4-T-8,AB=AE,∠B=∠E,BC=ED,F是CD的中点,则AF⊥CD吗?试说明理由. 图4-T-8本章总结提升解:连接AC,AD,由AB=AE,∠B=∠E,BC=DE,根据“SAS”可知△ABC≌△AED,
根据全等三角形的对应边相等可知AC=AD.
由AC=AD,CF=DF,AF=AF(公共边),
根据“SSS”可知△ACF≌△ADF.
根据全等三角形的对应角相等可知∠AFC=∠AFD.
又由于F在直线CD上,可得∠AFC=90°,
即AF⊥CD.本章总结提升[点析]本题进行了两次三角形全等的证明,在证明线段、角等问题时往往转化为证明三角形全等,从而达到证明的目的. 本章总结提升? 类型八 利用三角形全等测距离 例11 如图4-T-9所示,A,B两个建筑物分别位于河的两岸,要测得它们之间的距离,可以从B出发沿河岸画一条射线BF,在BF上截取BC=CD,过D作DE∥AB,使E,C,A在同一条直线上,则DE的长就是A,B之间的距离,请你说明道理. 图4-T-9本章总结提升[解析] 因为DE∥AB,可得∠A=∠E,∠ABC=∠CDE.又因为BC=CD,于是可得△ABC≌△EDC,可得AB=DE.解: ∵DE∥AB(作图),
∴∠A=∠E,∠ABC=∠CDE(两直线平行,内错角相等).
又∵BC=CD(已知),∴△ABC≌△EDC(AAS),
∴AB=DE(全等三角形的对应边相等).
本章总结提升[点析]测量无法到达的问题时,可以将实际问题转化为数学问题来解决,本题巧妙地利用了三角形全等进行转化,从而达到测量的目的.
A.5 B.6 C.11 D.16[解析] C 已知三角形两边的长分别是4和10,所以第三边x的范围是6<x<14,在这个范围内,只有11符合.故选C.本章总结提升[点析] 已知三角形的两条边长,求第三边,根据“三角形两边之和大于第三边”和“三角形两边之差小于第三边”,可得“三角形的第三边大于两边之差且小于两边之和”,从而先求出第三边的范围,然后作出选择.本章总结提升例2 王伟准备用一段长30米的篱笆围成一个三角形形状的养兔圈,用于饲养家兔.已知第一条边长为a米,由于受地势限制,第二条边长只能比第一条边长的2倍多2米.
(1)请用a表示第三条边长;
(2)问第一条边长可以为8米吗?为什么?请说明理由;
(3)能否使得围成的养兔圈是等腰三角形?若能,说明你的围法;若不能,请说明理由.本章总结提升本章总结提升本章总结提升[点析]本题以构成三角形三边关系为载体,主要考查了整式计算与三角形的有关边知识的理解与运用,在探究等腰三角形的形状时要注意分类讨论,构建方程分析与解决实际问题.本章总结提升? 类型二 等腰三角形 例3 一个三角形的两条边相等,周长为18 cm,三角形一边长为4 cm,求其他两边长. [解析] 本题分两种情况:①腰长为4 cm,②底边长为4 cm.解答时要注意求出的边长要符合“三角形两边之和大于第三边”.本章总结提升本章总结提升[点析]等腰三角形是一种特殊而又十分重要的三角形,就是因为这种特殊性,在具体处理问题时往往又会出现错误,因此,同学们在求解有关等腰三角形的问题时一定要注意分类讨论.对于底和腰不等的等腰三角形,若条件中没有明确是底或腰时,应在符合三角形三边关系的前提下分类讨论. 本章总结提升? 类型三 与三角形的角有关的计算 例4 如图4-T-1,一个大型模板的设计要求是模板的BA边和CD边相交成50°角,DA边和CB边相交成30°角,如果通过测量∠A,∠B,∠C,∠D的度数来判断模板是否合格,你认为当∠D与∠B的度数相差多少时,模板刚好合格?图4-T-1本章总结提升[解析] 要判断∠D与∠B的度数相差多少时,模板刚好合格,可延长CD与BA,DA与CB,构造三角形,然后根据三角形内角和等于180°进行探究.解:当模板合格时,如图4-T-1,延长BA交CD的延长线于点E,则∠E=50°;延长DA交CB的延长线于点F,则∠F=30°,
由三角形的三个内角和等于180°,得
∠CBE+∠C+∠E=180°,∠CDF+∠C+∠F=180°,
所以∠CBE=180°-(∠E+∠C)=180°-(50°+∠C)=130°-∠C,本章总结提升∠CDF=180°-(∠F+∠C)=180°-(30°+∠C)=150°-∠C.
因为∠CDF-∠CBE=150°-∠C-(130°-∠C)=20°,
所以∠CDF比∠CBE大20°.
即∠D比∠B大20°时,模板刚好合格.
本章总结提升[点析]三角形的内角和等于180°,我们可以利用这一结论解决与角度计算有关的实际问题,解决问题的关键是如何将实际问题转化为数学问题.本章总结提升? 类型四 三角形中的重要线段例5 如图4-T-2,已知∠B=45°,∠C=75°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数. 图4-T-2本章总结提升本章总结提升本章总结提升图4-T-3[答案] 2本章总结提升本章总结提升[点析]解决本题的关键是利用三角形的面积关系,在高不变的情况下,底为中点或三等分点构成的三角形与原三角形的面积之间的关系,就是底之间的关系,注意数形结合及转换的数学思想方法. 本章总结提升? 类型五 尺规作图 例7 已知:线段a,c和∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.图4-T-4本章总结提升 解:如图4-T-5所示.①先画射线BC;图4-T-5本章总结提升②以∠α的顶点为圆心,任意长为半径画孤,分别交∠α的两边于A′,C′;
③以相同长度为半径,B为圆心,画弧,交BC于点F,以F为圆心,C′A′长为半径画弧,交已画弧于点E,连接EB,则∠EBF=∠α;
④在BF上取点C,使CB=a,以B为圆心,c为半径画圆交BE的延长线于点A,连接AC.△ABC即为所求作三角形.本章总结提升? 类型六 全等三角形中的开放性问题 例8 如图4-T-6所示,AB,CD相交于点O,AB=CD,试添加一个条件使得△AOD≌△COB,你添加的条件是__________(只需写一个).图4-T-6[答案] OA=OC或OB=OD本章总结提升[解析] 两个三角形全等的条件有“SAS”,“ASA”,“AAS”,“SSS”.结合题设中的已知,选择恰当的三角形全等条件是解决此类问题的关键.已知条件有AB=CD,隐含条件有∠AOD=∠COB,可选择“SAS”,填OA=OC或OB=OD.本章总结提升[点析]全等三角形是初中数学中最基础、最重要的一部分内容,本题是添加条件写结论的全开放型的创新题,这种类型的题目开放程度非常高,能激起同学们的挑战欲望和创新热情,实属好题. 本章总结提升? 类型七 全等三角形的性质与判定的综合应用 例9 如图4-T-7,已知点B,F,C,E在一条直线上,FB=CE,AC=DF.
能否由上面的已知条件说明AB∥ED?如果能,请给出说明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并说明理由.
供选择的三个条件(请从其中选择一个):
①AB=ED;②BC=EF; ③∠ACB=∠DFE.本章总结提升图4-T-7本章总结提升[解析] 由条件可知两三角形中具备了两边对应相等,可补充边借助“边边边”定理突破,也可补充这两边的夹角,借助“边角边”定理进行分析.解:由上面两条件不能说明AB∥ED.
有两种添加方法.
第一种:添加①AB=ED.
理由:因为FB=CE,所以BC=EF.本章总结提升又AC=DF,AB=ED,
所以△ABC≌△DEF.
所以∠B=∠E,
所以AB∥ED.
第二种:添加③∠ACB=∠DFE.
理由:因为FB=CE,
所以BC=EF.本章总结提升又∠ACB=∠DFE,AC=DF,
所以△ABC≌△DEF.
所以∠B=∠E,所以AB∥ED.[点析]近几年的各地中考中,全等三角形常以开放探究的形式出现,可能设置的问题结论不唯一,或条件不完备,即需要解题者依据题意确定结论或补全条件,或通过变换操作,或有关图形的动态变化导致某些图形、情境的变化,进而构建不同的数学模型,或选择不同的解题策略进行解答.本章总结提升例10 如图4-T-8,AB=AE,∠B=∠E,BC=ED,F是CD的中点,则AF⊥CD吗?试说明理由. 图4-T-8本章总结提升解:连接AC,AD,由AB=AE,∠B=∠E,BC=DE,根据“SAS”可知△ABC≌△AED,
根据全等三角形的对应边相等可知AC=AD.
由AC=AD,CF=DF,AF=AF(公共边),
根据“SSS”可知△ACF≌△ADF.
根据全等三角形的对应角相等可知∠AFC=∠AFD.
又由于F在直线CD上,可得∠AFC=90°,
即AF⊥CD.本章总结提升[点析]本题进行了两次三角形全等的证明,在证明线段、角等问题时往往转化为证明三角形全等,从而达到证明的目的. 本章总结提升? 类型八 利用三角形全等测距离 例11 如图4-T-9所示,A,B两个建筑物分别位于河的两岸,要测得它们之间的距离,可以从B出发沿河岸画一条射线BF,在BF上截取BC=CD,过D作DE∥AB,使E,C,A在同一条直线上,则DE的长就是A,B之间的距离,请你说明道理. 图4-T-9本章总结提升[解析] 因为DE∥AB,可得∠A=∠E,∠ABC=∠CDE.又因为BC=CD,于是可得△ABC≌△EDC,可得AB=DE.解: ∵DE∥AB(作图),
∴∠A=∠E,∠ABC=∠CDE(两直线平行,内错角相等).
又∵BC=CD(已知),∴△ABC≌△EDC(AAS),
∴AB=DE(全等三角形的对应边相等).
本章总结提升[点析]测量无法到达的问题时,可以将实际问题转化为数学问题来解决,本题巧妙地利用了三角形全等进行转化,从而达到测量的目的.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
