【备课无忧】人教版六年级下册-5.3 鸽巢问题的应用(教学课件).pptx
文档属性
| 名称 | 【备课无忧】人教版六年级下册-5.3 鸽巢问题的应用(教学课件).pptx |  | |
| 格式 | pptx | ||
| 文件大小 | 17.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-06 11:11:57 | ||
图片预览






文档简介
(共22张PPT)
人教版数学六年级下册
第
五
单
元
3.鸽巢问题的应用
11 只鸽子飞进了 4 个鸽笼,总有一个鸽笼至少飞进了 3 只鸽子。为什么?
11÷4=2(个)……3(只)
2+1=3(只)
因为平均每个鸽笼都飞进了2只鸽子,还剩下3只,不论怎么飞,总有1个鸽笼里至少飞进3只鸽子。
鸽巢原理:
把多于kn个物体任意分放进n个“鸽巢”中(k、n均
是非0自然数),总有一个“鸽巢”中至少放进(k+1)个物体。
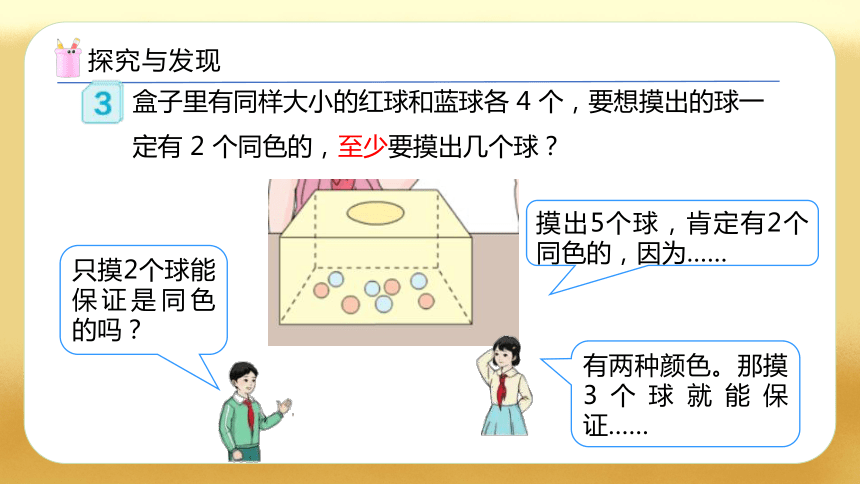
盒子里有同样大小的红球和蓝球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
摸出5个球,肯定有2个同色的,因为……
有两种颜色。那摸3个球就能保证……
只摸2个球能保证是同色的吗?
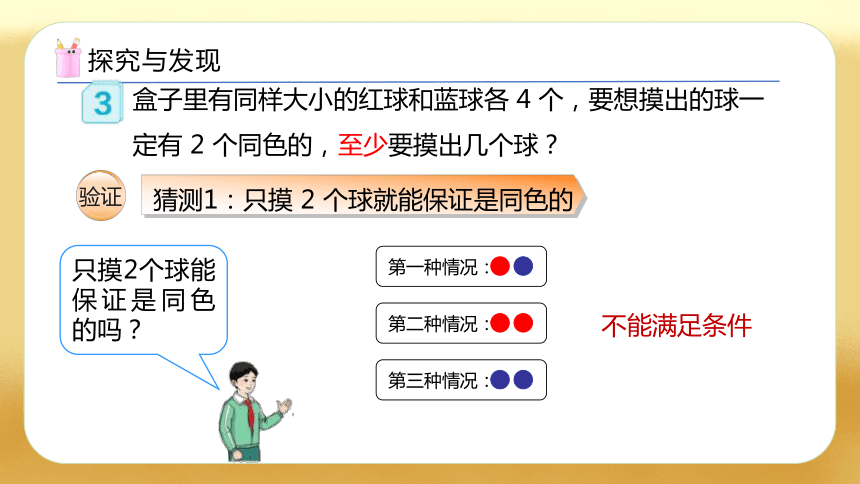
盒子里有同样大小的红球和蓝球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
猜测1:只摸 2 个球就能保证是同色的
验证
第一种情况:
不能满足条件
第二种情况:
第三种情况:
只摸2个球能保证是同色的吗?
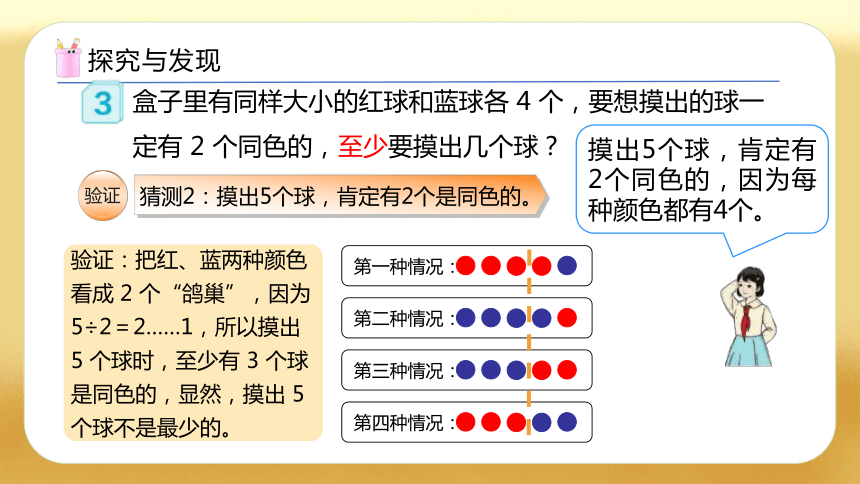
盒子里有同样大小的红球和蓝球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
摸出5个球,肯定有2个同色的,因为每种颜色都有4个。
验证
猜测2:摸出5个球,肯定有2个是同色的。
验证:把红、蓝两种颜色看成 2 个“鸽巢”,因为 5÷2=2……1,所以摸出 5 个球时,至少有 3 个球是同色的,显然,摸出 5 个球不是最少的。
第一种情况:
第二种情况:
第三种情况:
第四种情况:
盒子里有同样大小的红球和蓝球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
有两种颜色。那摸3个球就能保证……
验证
猜测3:有两种颜色。那摸 3 个球就能保证有 2 个同色的球。
最不利原则
第一种情况:
第一种情况:
只要摸出的球数比它们的颜色种数多1,就能保证有两个球同色。
摸出的球数=颜色种类+1
1. 向东小学六年级共有367名学生,其中六(2)班有49名学生。
他们说得对吗?为什么?
367÷365=1……2
1+1=2
49÷12=4……1
4+1=5
六年级里至少有两人的生日是同一天。
六(2)班中至少有5人是同一个月出生的。
教材第65页“做一做”第1题
2. 把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少取多少个球,可以保证取到两个颜色相同的球?
假设我们每种颜色的都拿一个,需要拿 4 个,但是没有同色的,要想有同色的需要再拿1个球,不论是哪一种颜色的,都一定有 2 个同色的。
教材第69页“做一做”第2题
(1)一副扑克牌有54张,至少抽( )张才能保证其中最少有一张是“A”。
(2)有黑、白色的同一品牌的袜子各5只,如果闭着眼睛,至少拿出( )只才能使拿出的袜子中一定有一双是同色的。
3. 填空乐园。
51
3
(3)箱子中有5个篮球,4个红球,至少要取出( )个球才能保证两种颜色的球都有。至少要取( )个球才能保证有2个红球。
6
7
4.箱子里有黑、白两种颜色的手套各16只。(同色的可以配1双手套)
(1)至少摸出多少只,可以配1双手套?
2+1=3(只)
至少摸出3只,可以配1双手套。
4.箱子里有黑、白两种颜色的手套各16只。(同色的可以配1双手套)
(2)至少摸出多少只,可以配2双手套?
3+1+1=5(只)
至少摸出5只,可以配2双手套。
4.箱子里有黑、白两种颜色的手套各16只。(同色的可以配1双手套)
(3)至少摸出多少只,一定有一双黑色手套?
16+2=18(只)
至少摸出18只,一定有1双黑色手套。
点击输入标题
点此输入内容或者复制您的内容在这里,在此框中选择粘贴,并选择只保留文字。点此输入内容或者复制您的内容在这里,在此框中选择粘贴,并选择只保留文字。
点击此处输入标题
今天我学会了……
课堂总结
1. 根据题意,把实际问题转化为鸽巢问题,即构造鸽巢和找出要分放的物体。
2. 把物体放进鸽巢,考虑最不利原则进行分析。
3. 说明理由,得出结论。
利用鸽巢原理解决实际问题的方法:
学习态度
学习自信
学习合作
素养评价
1.完成《分层作业》中对应练习。
2.预习下一节内容。
课后作业
课程结束
人教版数学六年级下册
第
五
单
元
3.鸽巢问题的应用
11 只鸽子飞进了 4 个鸽笼,总有一个鸽笼至少飞进了 3 只鸽子。为什么?
11÷4=2(个)……3(只)
2+1=3(只)
因为平均每个鸽笼都飞进了2只鸽子,还剩下3只,不论怎么飞,总有1个鸽笼里至少飞进3只鸽子。
鸽巢原理:
把多于kn个物体任意分放进n个“鸽巢”中(k、n均
是非0自然数),总有一个“鸽巢”中至少放进(k+1)个物体。
盒子里有同样大小的红球和蓝球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
摸出5个球,肯定有2个同色的,因为……
有两种颜色。那摸3个球就能保证……
只摸2个球能保证是同色的吗?
盒子里有同样大小的红球和蓝球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
猜测1:只摸 2 个球就能保证是同色的
验证
第一种情况:
不能满足条件
第二种情况:
第三种情况:
只摸2个球能保证是同色的吗?
盒子里有同样大小的红球和蓝球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
摸出5个球,肯定有2个同色的,因为每种颜色都有4个。
验证
猜测2:摸出5个球,肯定有2个是同色的。
验证:把红、蓝两种颜色看成 2 个“鸽巢”,因为 5÷2=2……1,所以摸出 5 个球时,至少有 3 个球是同色的,显然,摸出 5 个球不是最少的。
第一种情况:
第二种情况:
第三种情况:
第四种情况:
盒子里有同样大小的红球和蓝球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
有两种颜色。那摸3个球就能保证……
验证
猜测3:有两种颜色。那摸 3 个球就能保证有 2 个同色的球。
最不利原则
第一种情况:
第一种情况:
只要摸出的球数比它们的颜色种数多1,就能保证有两个球同色。
摸出的球数=颜色种类+1
1. 向东小学六年级共有367名学生,其中六(2)班有49名学生。
他们说得对吗?为什么?
367÷365=1……2
1+1=2
49÷12=4……1
4+1=5
六年级里至少有两人的生日是同一天。
六(2)班中至少有5人是同一个月出生的。
教材第65页“做一做”第1题
2. 把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少取多少个球,可以保证取到两个颜色相同的球?
假设我们每种颜色的都拿一个,需要拿 4 个,但是没有同色的,要想有同色的需要再拿1个球,不论是哪一种颜色的,都一定有 2 个同色的。
教材第69页“做一做”第2题
(1)一副扑克牌有54张,至少抽( )张才能保证其中最少有一张是“A”。
(2)有黑、白色的同一品牌的袜子各5只,如果闭着眼睛,至少拿出( )只才能使拿出的袜子中一定有一双是同色的。
3. 填空乐园。
51
3
(3)箱子中有5个篮球,4个红球,至少要取出( )个球才能保证两种颜色的球都有。至少要取( )个球才能保证有2个红球。
6
7
4.箱子里有黑、白两种颜色的手套各16只。(同色的可以配1双手套)
(1)至少摸出多少只,可以配1双手套?
2+1=3(只)
至少摸出3只,可以配1双手套。
4.箱子里有黑、白两种颜色的手套各16只。(同色的可以配1双手套)
(2)至少摸出多少只,可以配2双手套?
3+1+1=5(只)
至少摸出5只,可以配2双手套。
4.箱子里有黑、白两种颜色的手套各16只。(同色的可以配1双手套)
(3)至少摸出多少只,一定有一双黑色手套?
16+2=18(只)
至少摸出18只,一定有1双黑色手套。
点击输入标题
点此输入内容或者复制您的内容在这里,在此框中选择粘贴,并选择只保留文字。点此输入内容或者复制您的内容在这里,在此框中选择粘贴,并选择只保留文字。
点击此处输入标题
今天我学会了……
课堂总结
1. 根据题意,把实际问题转化为鸽巢问题,即构造鸽巢和找出要分放的物体。
2. 把物体放进鸽巢,考虑最不利原则进行分析。
3. 说明理由,得出结论。
利用鸽巢原理解决实际问题的方法:
学习态度
学习自信
学习合作
素养评价
1.完成《分层作业》中对应练习。
2.预习下一节内容。
课后作业
课程结束
