8.3 实数及其简单运算(1)教案 2024-2025学年数学人教版七年级下册
文档属性
| 名称 | 8.3 实数及其简单运算(1)教案 2024-2025学年数学人教版七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 49.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-06 21:34:30 | ||
图片预览


文档简介
8.3 实数及其简单运算
第1课时
【教学目标】
1.了解无理数和实数的概念.
2.知道实数与数轴上的点具有一一对应关系,初步体会“数形结合”的数学思想.
3.会求实数的相反数与绝对值,会对实数进行简单的运算.
4.经历从有理数扩充到实数及对实数进行分类的过程,发展学生的分类意识及集合思想,通过在数轴上表示实数进一步发展数形结合意识.
5.在探究活动中学会用数轴上的点表示实数,渗透数形结合思想,培养学生的探究能力.
【重点难点】
重点:1.了解无理数和实数的概念,知道实数与数轴上的点的一一对应关系.
2.知道有理数的运算律和运算性质同样适合于实数的运算,并会进行简单的运算.
难点:1.对无理数的认识.
2.认识和理解有理数的一些概念和运算在实数中仍适用的这种扩充.
【教学过程】
一、创设情境
1.(用课件出示古希腊数学家毕达哥拉斯的画像)
古希腊著名的数学家毕达哥拉斯曾说过这样的一句话:“世界上只有整数和分数,除此之外就再也没有什么别的数了!”同学们,你们赞成这位数学家的说法吗 学完本节课后相信你能得到正确的答案.
2.问题1:请把下列有理数写成小数形式:,-,,,4,.
3.问题2:通过解题,你有什么发现
二、新知探究
探究点1:无理数的定义及实数的分类
问题1:你能将下列分数写成小数的形式吗 你能将整数写成小数的形式吗
【试一试】
1.使用计算器计算,把下列有理数写成小数的形式,你有什么发现
3,,,
动手试一试,说说你的发现并与同学交流.
(结论:上面的有理数都可以写成有限小数或无限循环小数的形式)
可以在此基础上启发学生得到结论:任何一个有理数都可以写成有限小数或无限循环小数的形式.
2.追问:任何一个有限小数或无限循环小数都能化成分数吗
(任何一个有限小数或无限循环小数都能化成分数,所以任何一个有限小数或无限循环小数都是有理数.)
问题2:我们学过的数都可以化为有限小数或无限循环小数吗 能举列说明吗
要点归纳:
1.无理数的定义:无限不循环小数叫做无理数.
2.实数的定义:有理数和无理数统称实数.
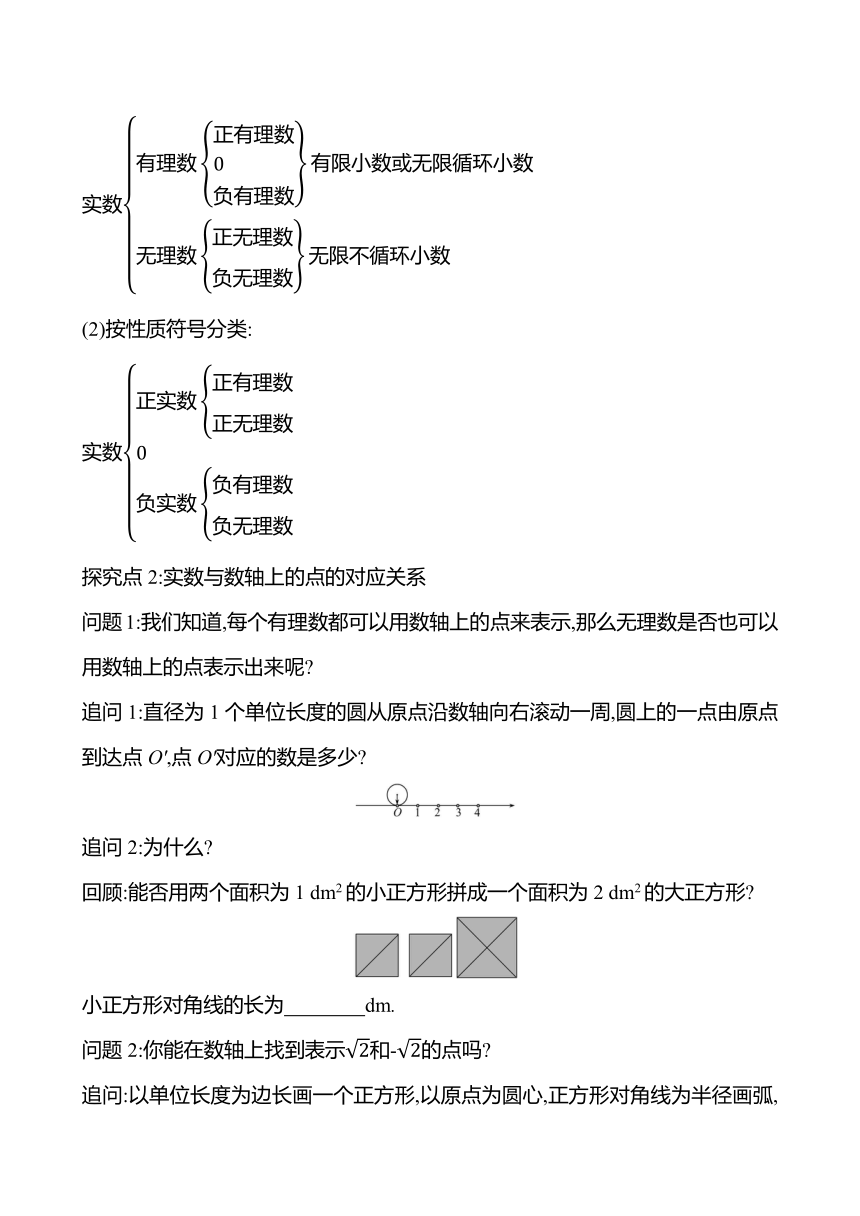
3.实数的分类:
(1)按定义分类:
实数
(2)按性质符号分类:
实数
探究点2:实数与数轴上的点的对应关系
问题1:我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢
追问1:直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O',点O'对应的数是多少
追问2:为什么
回顾:能否用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形
小正方形对角线的长为 dm.
问题2:你能在数轴上找到表示和-的点吗
追问:以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正半轴的交点表示什么 与负半轴的交点表示什么
要点归纳:事实上,每一个无理数都可以用数轴上的点表示出来.这就是说,数轴上的点有些表示有理数,有些表示无理数.当从有理数扩充到实数以后,实数与数轴上的点就是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都是表示一个实数.对于数轴上的两个点,右边的点所表示的实数比左边的点所表示的实数大.
例题讲解
例 把下列各数填入相应的集合内:
-π,,3.1,,0.808 008 000 8 …(相邻两个8之间的0的个数逐次加1),,,,-,,,
整数集合{ }
正数集合{ }
负数集合{ }
有理数集合{ }
无理数集合{ }
【方法指导】 无理数的特征:(1)圆周率π及一些含有π的数;(2)开不尽方的数(注意:带根号的数不一定是无理数);(3)有一定的规律,但不循环的无限小数.
三、检测反馈
1.判断题
①实数不是有理数就是无理数.( )
②无理数都是无限不循环小数.( )
③带根号的数都是无理数.( )
④无理数都是无限小数.( )
⑤无理数一定都带根号.( )
⑥两个无理数之和一定是无理数.( )
⑦两个无理数之积不一定是无理数.( )
2.实数,,,3-,,0.505 005 000 5…中,无理数有( )
A.4个 B.3个
C.2个 D.1个
3.下列4个数:,,π,()0,其中无理数是( )
A. B.
C.π D.()0
4.若无理数a满足:15.把下列各数分别填入相应的集合内:
-2.5,0,8,-2,,,-0.525 225 222 5…(每两个5之间依次增加1个2).
(1)正数集合{ }.
(2)负数集合{ }.
(3)整数集合{ }.
(4)无理数集合{ }.
四、本课小结
师生交流:通过本节课的学习,说说你的收获.
1.无理数的概念和特征.
2.引导学生从数系、分类、数形结合角度总结实数的概念、分类及实数和数轴上的点之间的关系.
五、布置作业
教材第54页练习P57习题8.3第1,2题
六、板书设计
8.3 实数及其简单运算 (第1课时) 无理数 实数的分 例1 探究点拨 定义: 类: ……… ……… ……… ……… ……… ……… 特征: ……… ……… ……… ……… ……… ……… ……… ……… ……… ……… ………
七、教学反思
波利亚认为,“头脑不活动起来,是很难学到什么东西的,也肯定学不到更多的东西”“学东西的最好途径是亲自去发现它”“学生在学习中寻求欢乐”.在本节课的教学设计中注意从学生的认知水平和亲身感受出发,创设学习情境,提高学生学习数学的积极性和学习兴趣,设计系列活动让学生经历不同的学习过程.在活动过程中让学生动手试一试,说说自己的发现并与同学交流讨论,在交流中尝试得出结论:任何一个有理数都可以写成有限小数或无限循环小数的形式,进一步地提出问题:任何一个有限小数或无限循环小数都能化成分数吗 引入了无理数和实数的概念后,要求学生对所学过的数按照一定的标准进行分类.分类思想是解决数学问题的常用思想,在教学过程中,教师应该创造条件,让学生体会分类标准与分类结果之间的关系.本课提出的问题“你能尝试着找出三个无理数来吗 ”具有较大的开放性,给学生提供了思维空间,能促使学生积极主动地参与到数学学习过程中,亲自体验知识的形成过程.
第1课时
【教学目标】
1.了解无理数和实数的概念.
2.知道实数与数轴上的点具有一一对应关系,初步体会“数形结合”的数学思想.
3.会求实数的相反数与绝对值,会对实数进行简单的运算.
4.经历从有理数扩充到实数及对实数进行分类的过程,发展学生的分类意识及集合思想,通过在数轴上表示实数进一步发展数形结合意识.
5.在探究活动中学会用数轴上的点表示实数,渗透数形结合思想,培养学生的探究能力.
【重点难点】
重点:1.了解无理数和实数的概念,知道实数与数轴上的点的一一对应关系.
2.知道有理数的运算律和运算性质同样适合于实数的运算,并会进行简单的运算.
难点:1.对无理数的认识.
2.认识和理解有理数的一些概念和运算在实数中仍适用的这种扩充.
【教学过程】
一、创设情境
1.(用课件出示古希腊数学家毕达哥拉斯的画像)
古希腊著名的数学家毕达哥拉斯曾说过这样的一句话:“世界上只有整数和分数,除此之外就再也没有什么别的数了!”同学们,你们赞成这位数学家的说法吗 学完本节课后相信你能得到正确的答案.
2.问题1:请把下列有理数写成小数形式:,-,,,4,.
3.问题2:通过解题,你有什么发现
二、新知探究
探究点1:无理数的定义及实数的分类
问题1:你能将下列分数写成小数的形式吗 你能将整数写成小数的形式吗
【试一试】
1.使用计算器计算,把下列有理数写成小数的形式,你有什么发现
3,,,
动手试一试,说说你的发现并与同学交流.
(结论:上面的有理数都可以写成有限小数或无限循环小数的形式)
可以在此基础上启发学生得到结论:任何一个有理数都可以写成有限小数或无限循环小数的形式.
2.追问:任何一个有限小数或无限循环小数都能化成分数吗
(任何一个有限小数或无限循环小数都能化成分数,所以任何一个有限小数或无限循环小数都是有理数.)
问题2:我们学过的数都可以化为有限小数或无限循环小数吗 能举列说明吗
要点归纳:
1.无理数的定义:无限不循环小数叫做无理数.
2.实数的定义:有理数和无理数统称实数.
3.实数的分类:
(1)按定义分类:
实数
(2)按性质符号分类:
实数
探究点2:实数与数轴上的点的对应关系
问题1:我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢
追问1:直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O',点O'对应的数是多少
追问2:为什么
回顾:能否用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形
小正方形对角线的长为 dm.
问题2:你能在数轴上找到表示和-的点吗
追问:以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正半轴的交点表示什么 与负半轴的交点表示什么
要点归纳:事实上,每一个无理数都可以用数轴上的点表示出来.这就是说,数轴上的点有些表示有理数,有些表示无理数.当从有理数扩充到实数以后,实数与数轴上的点就是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都是表示一个实数.对于数轴上的两个点,右边的点所表示的实数比左边的点所表示的实数大.
例题讲解
例 把下列各数填入相应的集合内:
-π,,3.1,,0.808 008 000 8 …(相邻两个8之间的0的个数逐次加1),,,,-,,,
整数集合{ }
正数集合{ }
负数集合{ }
有理数集合{ }
无理数集合{ }
【方法指导】 无理数的特征:(1)圆周率π及一些含有π的数;(2)开不尽方的数(注意:带根号的数不一定是无理数);(3)有一定的规律,但不循环的无限小数.
三、检测反馈
1.判断题
①实数不是有理数就是无理数.( )
②无理数都是无限不循环小数.( )
③带根号的数都是无理数.( )
④无理数都是无限小数.( )
⑤无理数一定都带根号.( )
⑥两个无理数之和一定是无理数.( )
⑦两个无理数之积不一定是无理数.( )
2.实数,,,3-,,0.505 005 000 5…中,无理数有( )
A.4个 B.3个
C.2个 D.1个
3.下列4个数:,,π,()0,其中无理数是( )
A. B.
C.π D.()0
4.若无理数a满足:1
-2.5,0,8,-2,,,-0.525 225 222 5…(每两个5之间依次增加1个2).
(1)正数集合{ }.
(2)负数集合{ }.
(3)整数集合{ }.
(4)无理数集合{ }.
四、本课小结
师生交流:通过本节课的学习,说说你的收获.
1.无理数的概念和特征.
2.引导学生从数系、分类、数形结合角度总结实数的概念、分类及实数和数轴上的点之间的关系.
五、布置作业
教材第54页练习P57习题8.3第1,2题
六、板书设计
8.3 实数及其简单运算 (第1课时) 无理数 实数的分 例1 探究点拨 定义: 类: ……… ……… ……… ……… ……… ……… 特征: ……… ……… ……… ……… ……… ……… ……… ……… ……… ……… ………
七、教学反思
波利亚认为,“头脑不活动起来,是很难学到什么东西的,也肯定学不到更多的东西”“学东西的最好途径是亲自去发现它”“学生在学习中寻求欢乐”.在本节课的教学设计中注意从学生的认知水平和亲身感受出发,创设学习情境,提高学生学习数学的积极性和学习兴趣,设计系列活动让学生经历不同的学习过程.在活动过程中让学生动手试一试,说说自己的发现并与同学交流讨论,在交流中尝试得出结论:任何一个有理数都可以写成有限小数或无限循环小数的形式,进一步地提出问题:任何一个有限小数或无限循环小数都能化成分数吗 引入了无理数和实数的概念后,要求学生对所学过的数按照一定的标准进行分类.分类思想是解决数学问题的常用思想,在教学过程中,教师应该创造条件,让学生体会分类标准与分类结果之间的关系.本课提出的问题“你能尝试着找出三个无理数来吗 ”具有较大的开放性,给学生提供了思维空间,能促使学生积极主动地参与到数学学习过程中,亲自体验知识的形成过程.
同课章节目录
