北师大版数学八年级下册第六章平行四边形第1节平行四边形的性质课时练习
文档属性
| 名称 | 北师大版数学八年级下册第六章平行四边形第1节平行四边形的性质课时练习 |
|
|
| 格式 | doc | ||
| 文件大小 | 391.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-10 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
北师大版数学八年级下册6.1平行四边形的性质课时练习
一、选择题
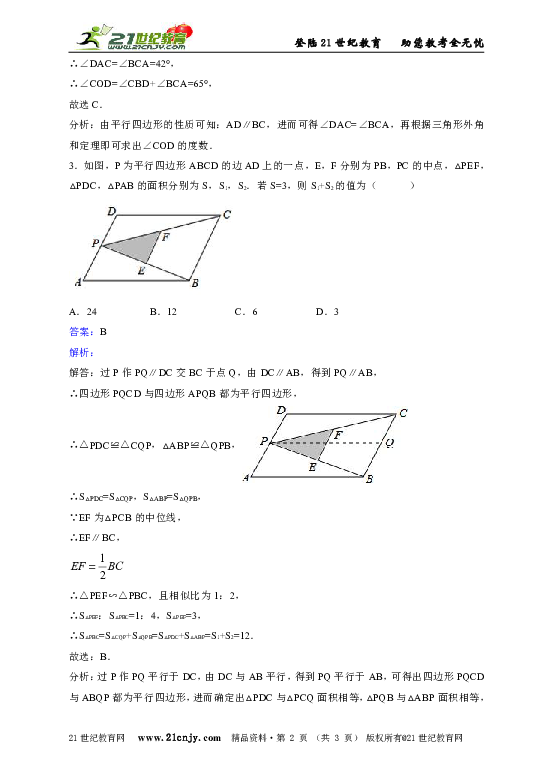
1.如图,在 ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长等于( )
A.8cm B.6cm C.4cm D.2cm
答案:C
解析:
解答:∵四边形ABCD是平行四边形,
∴BC=AD=12cm,AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BEA=∠BAE,
∴BE=AB=8cm,
∴CE=BC-BE=4cm.
故答案为:C.
分析:由平行四边形的性质得出BC=AD=12cm,AD∥BC,得出∠DAE=∠BEA,证出∠BEA=∠BAE,得出BE=AB,即可得出CE的长.
2.在 ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )
A.61° B.63° C.65° D.67°
答案:C
解析:
解答:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠BCA=42°,
∴∠COD=∠CBD+∠BCA=65°,
故选C.
分析:由平行四边形的性质可知:AD∥BC,进而可得∠DAC=∠BCA,再根据三角形外角和定理即可求出∠COD的度数.
3.如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )
A.24 B.12 C.6 D.3
答案:B
解析:
解答:过P作PQ∥DC交BC于点Q,由DC∥AB,得到PQ∥AB,
∴四边形PQCD与四边形APQB都为平行四边形,
∴△PDC≌△CQP,△ABP≌△QPB,
∴S△PDC=S△CQP,S△ABP=S△QPB,
∵EF为△PCB的中位线,
∴EF∥BC,
∴△PEF∽△PBC,且相似比为1:2,
∴S△PEF:S△PBC=1:4,S△PEF=3,
∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=S1+S2=12.
故选:B.
分析:过P作PQ平行于DC,由DC与AB平行,得到PQ平行于AB,可得出四边形PQCD与ABQP都为平行四边形,进而确定出△PDC与△PCQ面积相等,△PQB与△ABP面积相等,再由EF为△BPC的中位线,利用中位线定理得到EF为BC的一半,且EF平行于BC,得出△PEF与△PBC相似,相似比为1:2,面积之比为1:4,求出△PBC的面积,而△PBC面积=△CPQ面积+△PBQ面积,即为△PDC面积+△PAB面积,即为平行四边形面积的一半,即可求出所求的面积.
4.如图, ABCD的对角线AC、BD相交于点O,则下列说法一定正确的是( )
A.AO=OD B.AO⊥OD C.AO=OC D.AO⊥AB
答案:C
解析:
解答:对角线不一定相等,A错误;、
对角线不一定互相垂直,B错误;
对角线互相平分,C正确;
对角线与边不一定垂直,D错误.
故选:C.
分析:根据平行四边形的性质:对边平行且相等,对角线互相平分进行判断即可.
5.平行四边形ABCD的周长32,5AB=3BC,则对角线AC的取值范围为( )
A.6<AC<10 B.6<AC<16 C.10<AC<16 D.4<AC<16
答案:D
解析:
解答:∵平行四边形ABCD的周长32,5AB=3BC,
∴2(AB+BC)=2(BC+BC)=32,
∴BC=10,
∴AB=6,
∴BC-AB<AC<BC+AB,即4<AC<16.
故选D.
分析:根据平行四边形周长公式求得AB、BC的长度,然后由三角形的三边关系来求对角线AC的取值范围.
6.平行四边形的对角线一定具有的性质是( )
A.相等 B.互相平分 C.互相垂直 D.互相垂直且相等
答案:B
解析:
解答:平行四边形的对角线互相平分,
故选:B.
分析:根据平行四边形的对角线互相平分可得答案.
7.如图,在平行四边形ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是( )
A.7 B.10 C.11 D.12
答案:B
解析:
解答:∵AC的垂直平分线交AD于E,
∴AE=EC,
∵四边形ABCD是平行四边形,
∴DC=AB=4,AD=BC=6,
∴△CDE的周长为:EC+CD+ED=AD+CD=6+4=10,
故选:B.
分析:根据线段垂直平分线的性质可得AE=EC,再根据平行四边形的性质可得DC=AB=4,AD=BC=6,进而可以算出△CDE的周长.
8. 如图, ABCD中,BC=BD,∠C=74°,则∠ADB的度数是( )
A.16° B.22° C.32° D.68°
答案:C
解析:
解答:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C+∠ADC=180°,
∵∠C=74°,
∴∠ADC=106°,
∵BC=BD,
∴∠C=∠BDC=74°,
∴∠ADB=106°-74°=32°,
故选:C.
分析:根据平行四边形的性质可知:AD∥BC,所以∠C+∠ADC=180°,再由BC=BD可得∠C=∠BDC,进而可求出∠ADB的度数.
9. 如图,平行四边形ABCD的对角线AC、BD相交于点O,下列结论正确的是( )
A. S ABCD=4S△AOB B.AC=BD C.AC⊥BD D. ABCD是轴对称图形
答案:A
解析:
解答:A、∵平行四边形ABCD的对角线AC、BD相交于点O,
∴AO=CO,DO=BO,
∴S△AOD=S△DOC=S△BOC=S△AOB,
∴S ABCD=4S△AOB,故此选项正确;
B、无法得到AC=BD,故此选项错误;
C、无法得到AC⊥BD,故此选项错误;
D、 ABCD是中心对称图形,故此选项错误.
故选:A.
分析:根据平行四边形的性质分别判断得出答案即可.
10.如图所示的方格纸上有一平行四边形ABCD,其顶点均在网格线的交点上,且E点在AD上.今大华在方格纸网格线的交点上任取一点F,发现△FBC的面积比△EBC的面积大.判断下列哪一个图形可表示大华所取F点的位置?( )
A. B.
C. D.
答案:D
解析:
解答:A、点F到边BC的距离小于点E到边BC的距离,所以△FBC的面积<△EBC的面积,故本选项错误;
B、点F到边BC的距离小于点E到边BC的距离,所以△FBC的面积<△EBC的面积,故本选项错误;
C、点F到边BC的距离等于点E到边BC的距离,所以△FBC的面积=△EBC的面积,故本选项错误;
D、点F到边BC的距离大于点E到边BC的距离,所以△FBC的面积>△EBC的面积,故本选项正确.
故选D.
分析:根据两平行线间的距离相等,判断出各选项中点E、F到边BC的距离的大小,然后根据等底等高的三角形的面积相等解答.
11. 如图,等腰梯形ABCD下底与上底的差恰好等于腰长,DE∥AB.则∠DEC等于( )
A.75° B.60° C.45° D.30°
答案:C
解析:
解答:∵DE∥AB,AD∥BC
∴四边形ABED为平行四边形
∴AD=BE
∵BC-AD=AB=EC
∵等腰梯形ABCD
∴AB=DC=EC
∴△DEC为等边三角形
∴∠DEC=60°
故选B.
分析:通过上底的顶点D作DE∥AB,则AD=BE,EC就是两底的差,差等于一腰长,则△DEC是等边三角形,因而∠DEC=60°.
12. 如图,在 ABCD中,点M为CD的中点,且DC=2AD,则AM与BM的夹角的度数为( )
A.100° B.95° C.90° D.85°
答案:C
解析:解答: ABCD,
∴DC∥AB,AD∥BC,
∴∠DAB+∠CBA=180°,∠BAM=∠DMA,
∵点M为CD的中点,且DC=2AD,
∴DM=AD,
∴∠DMA=∠DAM,
∴∠DAM=∠BAM,
同理∠ABM=∠CBM,
即:
∴∠AMB=180°-90°=90°.
故选C.
分析:利用已知得到DM=AD,∠DAB+∠CBA=180°,进一步推出∠DAM=∠BAM,同理得到∠ABM=∠CBM,即:∠MAB+∠MBA=90°,利用三角形的内角和定理即可得到所选选项.
13. 如图等腰梯形ABCD,AE是BC边上的高.已知AE=4,CE=8,则梯形ABCD的面积是( )
A.16 B.32 C.24 D.48
答案:B
解析:
解:过点C作CF⊥AD交AD的延长线于点F,则∠CFD=90°.
∵四边形ABCD是等腰梯形
∴AD∥BC,AB=CD,
又∵AE是BC边上的高,
∴∠DAE=∠AEC=90°.
∴四边形AECF是矩形.
∴AE=CF.
在Rt△ABE和Rt△CDF中
∴Rt△ABE≌Rt△CDF(HL).
∴梯形ABCD的面积=矩形AECF的面积=4×8=32.
故选:B.
分析:过点C作CF⊥AD交AD的延长线于点F,先由等腰梯形的性质与矩形的判定方法及性质可得AE=CF.于是可证△ABE≌△CDF,所以梯形ABCD的面积=矩形AECF的面积=4×8=32.
14. 平行四边形的一条边长是12cm,那么它的两条对角线的长可能是( )
A.8cm和16cm B.10cm和16cm C.8cm和14cm D.8cm和12cm
答案:B
解析:
解答:A,4+8=12,不能构成三角形,不满足条件,故A选项错误;
B,5+8>12,能构成三角形,满足条件,故B选项正确.
C,4+7<12,不能构成三角形,不满足条件,故C选项错误;
D,4+6<12,不能构成三角形,不满足条件,故D选项错误.
故选:B.
分析:根据平行四边形的性质中,两条对角线的一半和一边构成三角形,利用三角形三边关系判断可知.
15. 如图, ABCD的周长为20cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A.4cm B.6cm C.8cm D.10cm
答案:D
解析:解答:∵四边形ABCD是平行四边形,
∴AD=BC,AO=OC,AB=CD,
∵ ABCD的周长为20cm,
∴AD+CD=10cm,
∵AO=OC,OE⊥AC,
∴AE=EC,
∴△DCE的周长为DE+EC+CD=DE+AE+CD=AD+CD=10cm,
故选D.
分析:根据平行四边形的性质得出AD=BC,AO=OC,AB=CD,求出AD+CD=10cm,根据线段垂直平分线性质求出AE=EC,求出∴△DCE的周长为DE+EC+CD=AD+CD,代入求出即可.
二、填空题
16.如图,在 ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB= _________cm.
答案:
解析:
解:∵四边形ABCD是平行四边形,
∴BC=AD=8cm,OA=OC= AC
∵AC⊥BC,
∴∠ACB=90°
∴AC=
∴OC=3
∴OB=
故答案为.
分析:由平行四边形的性质得出BC=AD=8cm,OA=OC=AC,由勾股定理求出AC,得出OC,再由勾股定理求出OB即可.
17. 用平行四边形纸条沿对边AB、CD上的点E、F所在的直线折成V字形图案,已知图中∠1=62°,则∠2的度数是________
答案:56°
解析:
解答:根据题意得:2∠1+∠2=180°,
∴∠2=180°-2×62°=56°,
故答案为:56°.
分析:由折叠的性质和平角的定义得出2∠1+∠2=180°,即可求出结果.
18.在 ABCD中,对角线AC,BD相交于点O,AB=8cm,BC=6cm.△AOB的周长是18cm,则△AOD的周长是__________ .
答案:16cm
解析:
解答:如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD=BC=6cm,
∵△AOB的周长是18cm,AB=8cm,
∴AB+OA+OB=18cm,
∴OA+OB=10cm,
∴△AOD的周长=OA+OD+AD=OA+OB+AD=10+6=16(cm);
故答案为:16cm.
分析:先由△AOB的周长求出OA+OB,再由平行四边形的性质得出OA+OD=OA+OB,即可求出△AOD的周长.
19. 一个平行四边形两对角之和为116°,则相邻的两内角分别是__________和_________
答案::58°;122°
解析:
解答:如图所示:
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠A+∠B=180°,
∵∠A+∠C=116°,
∴∠A=58°,∠B=180°-58°=122°;
故答案为:58°;122°.
分析:由平行四边形的性质得出∠A=∠C,∠A+∠B=180°,再由已知条件∠A+∠C=
116°,得出∠A,即可得出∠B.
20. 如图在平行四边形ABCD中,点E在CD边上运动(不与C、D两点重合),连接AE并延长与BC的延长线交于点F.连接BE、DF,若△BCE的面积是8,则△DEF的面积是 _________.
答案:8
解析:解答:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△ADE∽△FCE,
∴AE:EF=DE:CE,
∵S△BCE:S△ADE=CE:DE,S△DEF:S△ADE=EF:AE,
∴S△DEF=S△BCE=8.
故答案为:8.
分析:由四边形ABCD是平行四边形,可证得△ADE∽△FCE,由相似三角形的对应边成比例,可得AE:EF=DE:CE,又由S△BCE:S△ADE=CE:DE,S△DEF:S△ADE=EF:AE,即可得S△DEF=S△BCE=8.
三、解答题
21. 如图,在平行四边形ABCD中,若AB=6,AD=10,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长
答案:
解答:∵四边形ABCD为平行四边形,
∴AB=DC=6,AD=BC=10,AB∥DC.
∵AB∥DC,
∴∠1=∠3,
又∵BF平分∠ABC,
∴∠1=∠2,
∴∠2=∠3,
∴BC=CF=10,
∴DF=BF-DC=10-6=4.
解析:分析:首先根据平行四边形的性质可得AB=DC=6,AD=BC=10,AB∥DC,再根据平行线的性质与角平分线的性质证明∠2=∠3,根据等角对等边可得BC=CF=10,再用CF-CD即可算出DF的长.
22.在 ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
答案:证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB。
答案:解:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
.
∴AD=BC=DF=5,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.
解析:分析:(1)根据平行四边形的性质,可得AB与CD的关系,根据平行四边形的判定,可得BFDE是平行四边形,再根据矩形的判定,可得答案;
(2)根据平行线的性质,可得∠DFA=∠FAB,根据等腰三角形的判定与性质,可得∠DAF=∠DFA,根据角平分线的判定,可得答案.
23.如图,在 ABCD中,AC交BD于点O,点E、点F分别是OA、OC的中点,请判断
线段BE、DF的关系,并证明你的结论。
答案:
解答:由题意得:BE=DF,BE∥DF.理由如下:
连接DE、BF.
∵ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F分别是OA,OC的中点,
∴OE=OF,
∴BFDE是平行四边形,
∴BE=DF,BE∥DF.
解析:根据平行四边形的性质对角线互相平分得出OA=OC,OB=OD,利用中点的意义得出OE=OF,从而利用平行四边形的判定定理“对角线互相平分的四边形是平行四边形”判定BFDE是平行四边形,从而得出BE=DF,BE∥DF.
24.如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.
求证:(1)△AEH≌△CGF;
答案:证明:如图,∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△AEH与△CGF中
∴△AEH≌△CGF(SAS);
(2)四边形EFGH是菱形
答案:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
又∵AE=CG,AH=CF,
∴BE=DG,BF=DH,
在△BEF与△DGH中,
∴△BEF≌△DGH(SAS),
∴EF=GH.
又由(1)知,△AEH≌△CGF,
∴EH=GF,
∴四边形EFGH是平行四边形,
∴HG∥EF,
∴∠HGE=∠FEG,
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠HEG=∠HGE,
∴HE=HG,
∴四边形EFGH是菱形.
解析:分析:(1)由全等三角形的判定定理SAS证得结论;
(2)易证四边形EFGH是平行四边形,那么EF∥GH,那么∠HGE=∠FEG,而EG是角平分线,易得∠HEG=∠FEG,根据等量代换可得∠HEG=∠HGE,从而有HE=HG,易证四边形EFGH是菱形.
25.如图, ABCD中,E是BC边的中点,连接AE,F为CD边上一点,且满足∠DFA=2∠BAE.
(1)若∠D=105°,∠DAF=35°.求∠FAE的度数;20°
答案:
解:∵∠D=105°,∠DAF=35°,
∴∠DFA=180°-∠D-∠DAF=40°(三角形内角和定理).
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD(平行四边形对边平行且相等).
∴∠DFA=∠FAB=40°(两直线平行,内错角相等);
∵∠DFA=2∠BAE(已知),
∴∠FAB=2∠BAE(等量代换).
即∠FAE+∠BAE=2∠BAE.
∴∠FAE=∠BAE;
∴2∠FAE=40°,
∴∠FAE=20°;
(2)求证:AF=CD+CF
答案:证明:在AF上截取AG=AB,连接EG,CG.
∵∠FAE=∠BAE,AE=AE,
∴△AEG≌△AEB.
∴EG=BE,∠B=∠AGE;
又∵E为BC中点,∴CE=BE.
∴EG=EC,∴∠EGC=∠ECG;
∵AB∥CD,∴∠B+∠BCD=180°.
又∵∠AGE+∠EGF=180°,∠AGE=∠B,
∴∠BCF=∠EGF;
又∵∠EGC=∠ECG,
∴∠FGC=∠FCG,∴FG=FC;
又∵AG=AB,AB=CD,
∴AF=AG+GF=AB+FC=CD+FC.
解析:分析:(1)根据平行四边形的性质、平行线的性质证得∠DFA=∠FAB=40°;然后结合已知条件∠DFA=2∠BAE求得∠FAE=∠BAE,从而求得∠FAE的度数;
(2)在AF上截取AG=AB,连接EG,CG.利用全等三角形的判定定理SAS证得△AEG≌△AEB,由全等三角形的对应角相等、对应边相等知EG=BE,∠B=∠AGE;然后由中点E的性质平行线的性质以及等腰三角形的判定与性质求得CF=FG;最后根据线段间的和差关系证得结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 17 页 (共 18 页) 版权所有@21世纪教育网
北师大版数学八年级下册6.1平行四边形的性质课时练习
一、选择题
1.如图,在 ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长等于( )
A.8cm B.6cm C.4cm D.2cm
答案:C
解析:
解答:∵四边形ABCD是平行四边形,
∴BC=AD=12cm,AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BEA=∠BAE,
∴BE=AB=8cm,
∴CE=BC-BE=4cm.
故答案为:C.
分析:由平行四边形的性质得出BC=AD=12cm,AD∥BC,得出∠DAE=∠BEA,证出∠BEA=∠BAE,得出BE=AB,即可得出CE的长.
2.在 ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )
A.61° B.63° C.65° D.67°
答案:C
解析:
解答:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠BCA=42°,
∴∠COD=∠CBD+∠BCA=65°,
故选C.
分析:由平行四边形的性质可知:AD∥BC,进而可得∠DAC=∠BCA,再根据三角形外角和定理即可求出∠COD的度数.
3.如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )
A.24 B.12 C.6 D.3
答案:B
解析:
解答:过P作PQ∥DC交BC于点Q,由DC∥AB,得到PQ∥AB,
∴四边形PQCD与四边形APQB都为平行四边形,
∴△PDC≌△CQP,△ABP≌△QPB,
∴S△PDC=S△CQP,S△ABP=S△QPB,
∵EF为△PCB的中位线,
∴EF∥BC,
∴△PEF∽△PBC,且相似比为1:2,
∴S△PEF:S△PBC=1:4,S△PEF=3,
∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=S1+S2=12.
故选:B.
分析:过P作PQ平行于DC,由DC与AB平行,得到PQ平行于AB,可得出四边形PQCD与ABQP都为平行四边形,进而确定出△PDC与△PCQ面积相等,△PQB与△ABP面积相等,再由EF为△BPC的中位线,利用中位线定理得到EF为BC的一半,且EF平行于BC,得出△PEF与△PBC相似,相似比为1:2,面积之比为1:4,求出△PBC的面积,而△PBC面积=△CPQ面积+△PBQ面积,即为△PDC面积+△PAB面积,即为平行四边形面积的一半,即可求出所求的面积.
4.如图, ABCD的对角线AC、BD相交于点O,则下列说法一定正确的是( )
A.AO=OD B.AO⊥OD C.AO=OC D.AO⊥AB
答案:C
解析:
解答:对角线不一定相等,A错误;、
对角线不一定互相垂直,B错误;
对角线互相平分,C正确;
对角线与边不一定垂直,D错误.
故选:C.
分析:根据平行四边形的性质:对边平行且相等,对角线互相平分进行判断即可.
5.平行四边形ABCD的周长32,5AB=3BC,则对角线AC的取值范围为( )
A.6<AC<10 B.6<AC<16 C.10<AC<16 D.4<AC<16
答案:D
解析:
解答:∵平行四边形ABCD的周长32,5AB=3BC,
∴2(AB+BC)=2(BC+BC)=32,
∴BC=10,
∴AB=6,
∴BC-AB<AC<BC+AB,即4<AC<16.
故选D.
分析:根据平行四边形周长公式求得AB、BC的长度,然后由三角形的三边关系来求对角线AC的取值范围.
6.平行四边形的对角线一定具有的性质是( )
A.相等 B.互相平分 C.互相垂直 D.互相垂直且相等
答案:B
解析:
解答:平行四边形的对角线互相平分,
故选:B.
分析:根据平行四边形的对角线互相平分可得答案.
7.如图,在平行四边形ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是( )
A.7 B.10 C.11 D.12
答案:B
解析:
解答:∵AC的垂直平分线交AD于E,
∴AE=EC,
∵四边形ABCD是平行四边形,
∴DC=AB=4,AD=BC=6,
∴△CDE的周长为:EC+CD+ED=AD+CD=6+4=10,
故选:B.
分析:根据线段垂直平分线的性质可得AE=EC,再根据平行四边形的性质可得DC=AB=4,AD=BC=6,进而可以算出△CDE的周长.
8. 如图, ABCD中,BC=BD,∠C=74°,则∠ADB的度数是( )
A.16° B.22° C.32° D.68°
答案:C
解析:
解答:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C+∠ADC=180°,
∵∠C=74°,
∴∠ADC=106°,
∵BC=BD,
∴∠C=∠BDC=74°,
∴∠ADB=106°-74°=32°,
故选:C.
分析:根据平行四边形的性质可知:AD∥BC,所以∠C+∠ADC=180°,再由BC=BD可得∠C=∠BDC,进而可求出∠ADB的度数.
9. 如图,平行四边形ABCD的对角线AC、BD相交于点O,下列结论正确的是( )
A. S ABCD=4S△AOB B.AC=BD C.AC⊥BD D. ABCD是轴对称图形
答案:A
解析:
解答:A、∵平行四边形ABCD的对角线AC、BD相交于点O,
∴AO=CO,DO=BO,
∴S△AOD=S△DOC=S△BOC=S△AOB,
∴S ABCD=4S△AOB,故此选项正确;
B、无法得到AC=BD,故此选项错误;
C、无法得到AC⊥BD,故此选项错误;
D、 ABCD是中心对称图形,故此选项错误.
故选:A.
分析:根据平行四边形的性质分别判断得出答案即可.
10.如图所示的方格纸上有一平行四边形ABCD,其顶点均在网格线的交点上,且E点在AD上.今大华在方格纸网格线的交点上任取一点F,发现△FBC的面积比△EBC的面积大.判断下列哪一个图形可表示大华所取F点的位置?( )
A. B.
C. D.
答案:D
解析:
解答:A、点F到边BC的距离小于点E到边BC的距离,所以△FBC的面积<△EBC的面积,故本选项错误;
B、点F到边BC的距离小于点E到边BC的距离,所以△FBC的面积<△EBC的面积,故本选项错误;
C、点F到边BC的距离等于点E到边BC的距离,所以△FBC的面积=△EBC的面积,故本选项错误;
D、点F到边BC的距离大于点E到边BC的距离,所以△FBC的面积>△EBC的面积,故本选项正确.
故选D.
分析:根据两平行线间的距离相等,判断出各选项中点E、F到边BC的距离的大小,然后根据等底等高的三角形的面积相等解答.
11. 如图,等腰梯形ABCD下底与上底的差恰好等于腰长,DE∥AB.则∠DEC等于( )
A.75° B.60° C.45° D.30°
答案:C
解析:
解答:∵DE∥AB,AD∥BC
∴四边形ABED为平行四边形
∴AD=BE
∵BC-AD=AB=EC
∵等腰梯形ABCD
∴AB=DC=EC
∴△DEC为等边三角形
∴∠DEC=60°
故选B.
分析:通过上底的顶点D作DE∥AB,则AD=BE,EC就是两底的差,差等于一腰长,则△DEC是等边三角形,因而∠DEC=60°.
12. 如图,在 ABCD中,点M为CD的中点,且DC=2AD,则AM与BM的夹角的度数为( )
A.100° B.95° C.90° D.85°
答案:C
解析:解答: ABCD,
∴DC∥AB,AD∥BC,
∴∠DAB+∠CBA=180°,∠BAM=∠DMA,
∵点M为CD的中点,且DC=2AD,
∴DM=AD,
∴∠DMA=∠DAM,
∴∠DAM=∠BAM,
同理∠ABM=∠CBM,
即:
∴∠AMB=180°-90°=90°.
故选C.
分析:利用已知得到DM=AD,∠DAB+∠CBA=180°,进一步推出∠DAM=∠BAM,同理得到∠ABM=∠CBM,即:∠MAB+∠MBA=90°,利用三角形的内角和定理即可得到所选选项.
13. 如图等腰梯形ABCD,AE是BC边上的高.已知AE=4,CE=8,则梯形ABCD的面积是( )
A.16 B.32 C.24 D.48
答案:B
解析:
解:过点C作CF⊥AD交AD的延长线于点F,则∠CFD=90°.
∵四边形ABCD是等腰梯形
∴AD∥BC,AB=CD,
又∵AE是BC边上的高,
∴∠DAE=∠AEC=90°.
∴四边形AECF是矩形.
∴AE=CF.
在Rt△ABE和Rt△CDF中
∴Rt△ABE≌Rt△CDF(HL).
∴梯形ABCD的面积=矩形AECF的面积=4×8=32.
故选:B.
分析:过点C作CF⊥AD交AD的延长线于点F,先由等腰梯形的性质与矩形的判定方法及性质可得AE=CF.于是可证△ABE≌△CDF,所以梯形ABCD的面积=矩形AECF的面积=4×8=32.
14. 平行四边形的一条边长是12cm,那么它的两条对角线的长可能是( )
A.8cm和16cm B.10cm和16cm C.8cm和14cm D.8cm和12cm
答案:B
解析:
解答:A,4+8=12,不能构成三角形,不满足条件,故A选项错误;
B,5+8>12,能构成三角形,满足条件,故B选项正确.
C,4+7<12,不能构成三角形,不满足条件,故C选项错误;
D,4+6<12,不能构成三角形,不满足条件,故D选项错误.
故选:B.
分析:根据平行四边形的性质中,两条对角线的一半和一边构成三角形,利用三角形三边关系判断可知.
15. 如图, ABCD的周长为20cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A.4cm B.6cm C.8cm D.10cm
答案:D
解析:解答:∵四边形ABCD是平行四边形,
∴AD=BC,AO=OC,AB=CD,
∵ ABCD的周长为20cm,
∴AD+CD=10cm,
∵AO=OC,OE⊥AC,
∴AE=EC,
∴△DCE的周长为DE+EC+CD=DE+AE+CD=AD+CD=10cm,
故选D.
分析:根据平行四边形的性质得出AD=BC,AO=OC,AB=CD,求出AD+CD=10cm,根据线段垂直平分线性质求出AE=EC,求出∴△DCE的周长为DE+EC+CD=AD+CD,代入求出即可.
二、填空题
16.如图,在 ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB= _________cm.
答案:
解析:
解:∵四边形ABCD是平行四边形,
∴BC=AD=8cm,OA=OC= AC
∵AC⊥BC,
∴∠ACB=90°
∴AC=
∴OC=3
∴OB=
故答案为.
分析:由平行四边形的性质得出BC=AD=8cm,OA=OC=AC,由勾股定理求出AC,得出OC,再由勾股定理求出OB即可.
17. 用平行四边形纸条沿对边AB、CD上的点E、F所在的直线折成V字形图案,已知图中∠1=62°,则∠2的度数是________
答案:56°
解析:
解答:根据题意得:2∠1+∠2=180°,
∴∠2=180°-2×62°=56°,
故答案为:56°.
分析:由折叠的性质和平角的定义得出2∠1+∠2=180°,即可求出结果.
18.在 ABCD中,对角线AC,BD相交于点O,AB=8cm,BC=6cm.△AOB的周长是18cm,则△AOD的周长是__________ .
答案:16cm
解析:
解答:如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD=BC=6cm,
∵△AOB的周长是18cm,AB=8cm,
∴AB+OA+OB=18cm,
∴OA+OB=10cm,
∴△AOD的周长=OA+OD+AD=OA+OB+AD=10+6=16(cm);
故答案为:16cm.
分析:先由△AOB的周长求出OA+OB,再由平行四边形的性质得出OA+OD=OA+OB,即可求出△AOD的周长.
19. 一个平行四边形两对角之和为116°,则相邻的两内角分别是__________和_________
答案::58°;122°
解析:
解答:如图所示:
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠A+∠B=180°,
∵∠A+∠C=116°,
∴∠A=58°,∠B=180°-58°=122°;
故答案为:58°;122°.
分析:由平行四边形的性质得出∠A=∠C,∠A+∠B=180°,再由已知条件∠A+∠C=
116°,得出∠A,即可得出∠B.
20. 如图在平行四边形ABCD中,点E在CD边上运动(不与C、D两点重合),连接AE并延长与BC的延长线交于点F.连接BE、DF,若△BCE的面积是8,则△DEF的面积是 _________.
答案:8
解析:解答:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△ADE∽△FCE,
∴AE:EF=DE:CE,
∵S△BCE:S△ADE=CE:DE,S△DEF:S△ADE=EF:AE,
∴S△DEF=S△BCE=8.
故答案为:8.
分析:由四边形ABCD是平行四边形,可证得△ADE∽△FCE,由相似三角形的对应边成比例,可得AE:EF=DE:CE,又由S△BCE:S△ADE=CE:DE,S△DEF:S△ADE=EF:AE,即可得S△DEF=S△BCE=8.
三、解答题
21. 如图,在平行四边形ABCD中,若AB=6,AD=10,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长
答案:
解答:∵四边形ABCD为平行四边形,
∴AB=DC=6,AD=BC=10,AB∥DC.
∵AB∥DC,
∴∠1=∠3,
又∵BF平分∠ABC,
∴∠1=∠2,
∴∠2=∠3,
∴BC=CF=10,
∴DF=BF-DC=10-6=4.
解析:分析:首先根据平行四边形的性质可得AB=DC=6,AD=BC=10,AB∥DC,再根据平行线的性质与角平分线的性质证明∠2=∠3,根据等角对等边可得BC=CF=10,再用CF-CD即可算出DF的长.
22.在 ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
答案:证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB。
答案:解:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
.
∴AD=BC=DF=5,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.
解析:分析:(1)根据平行四边形的性质,可得AB与CD的关系,根据平行四边形的判定,可得BFDE是平行四边形,再根据矩形的判定,可得答案;
(2)根据平行线的性质,可得∠DFA=∠FAB,根据等腰三角形的判定与性质,可得∠DAF=∠DFA,根据角平分线的判定,可得答案.
23.如图,在 ABCD中,AC交BD于点O,点E、点F分别是OA、OC的中点,请判断
线段BE、DF的关系,并证明你的结论。
答案:
解答:由题意得:BE=DF,BE∥DF.理由如下:
连接DE、BF.
∵ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F分别是OA,OC的中点,
∴OE=OF,
∴BFDE是平行四边形,
∴BE=DF,BE∥DF.
解析:根据平行四边形的性质对角线互相平分得出OA=OC,OB=OD,利用中点的意义得出OE=OF,从而利用平行四边形的判定定理“对角线互相平分的四边形是平行四边形”判定BFDE是平行四边形,从而得出BE=DF,BE∥DF.
24.如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.
求证:(1)△AEH≌△CGF;
答案:证明:如图,∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△AEH与△CGF中
∴△AEH≌△CGF(SAS);
(2)四边形EFGH是菱形
答案:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
又∵AE=CG,AH=CF,
∴BE=DG,BF=DH,
在△BEF与△DGH中,
∴△BEF≌△DGH(SAS),
∴EF=GH.
又由(1)知,△AEH≌△CGF,
∴EH=GF,
∴四边形EFGH是平行四边形,
∴HG∥EF,
∴∠HGE=∠FEG,
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠HEG=∠HGE,
∴HE=HG,
∴四边形EFGH是菱形.
解析:分析:(1)由全等三角形的判定定理SAS证得结论;
(2)易证四边形EFGH是平行四边形,那么EF∥GH,那么∠HGE=∠FEG,而EG是角平分线,易得∠HEG=∠FEG,根据等量代换可得∠HEG=∠HGE,从而有HE=HG,易证四边形EFGH是菱形.
25.如图, ABCD中,E是BC边的中点,连接AE,F为CD边上一点,且满足∠DFA=2∠BAE.
(1)若∠D=105°,∠DAF=35°.求∠FAE的度数;20°
答案:
解:∵∠D=105°,∠DAF=35°,
∴∠DFA=180°-∠D-∠DAF=40°(三角形内角和定理).
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD(平行四边形对边平行且相等).
∴∠DFA=∠FAB=40°(两直线平行,内错角相等);
∵∠DFA=2∠BAE(已知),
∴∠FAB=2∠BAE(等量代换).
即∠FAE+∠BAE=2∠BAE.
∴∠FAE=∠BAE;
∴2∠FAE=40°,
∴∠FAE=20°;
(2)求证:AF=CD+CF
答案:证明:在AF上截取AG=AB,连接EG,CG.
∵∠FAE=∠BAE,AE=AE,
∴△AEG≌△AEB.
∴EG=BE,∠B=∠AGE;
又∵E为BC中点,∴CE=BE.
∴EG=EC,∴∠EGC=∠ECG;
∵AB∥CD,∴∠B+∠BCD=180°.
又∵∠AGE+∠EGF=180°,∠AGE=∠B,
∴∠BCF=∠EGF;
又∵∠EGC=∠ECG,
∴∠FGC=∠FCG,∴FG=FC;
又∵AG=AB,AB=CD,
∴AF=AG+GF=AB+FC=CD+FC.
解析:分析:(1)根据平行四边形的性质、平行线的性质证得∠DFA=∠FAB=40°;然后结合已知条件∠DFA=2∠BAE求得∠FAE=∠BAE,从而求得∠FAE的度数;
(2)在AF上截取AG=AB,连接EG,CG.利用全等三角形的判定定理SAS证得△AEG≌△AEB,由全等三角形的对应角相等、对应边相等知EG=BE,∠B=∠AGE;然后由中点E的性质平行线的性质以及等腰三角形的判定与性质求得CF=FG;最后根据线段间的和差关系证得结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 17 页 (共 18 页) 版权所有@21世纪教育网
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
