北师大版数学八年级下册第一章第三节线段的垂直平分线课时练习
文档属性
| 名称 | 北师大版数学八年级下册第一章第三节线段的垂直平分线课时练习 |  | |
| 格式 | doc | ||
| 文件大小 | 225.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-10 15:21:42 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
北师大版数学八年级下册1.3线段的垂直平分线课时练习
一、选择题
1.如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是( )
A. 8 B. 9 C. 10 D.11
答案:C
解析:解:∵ED是AB的垂直平分线,
∴AD=BD,
∵△BDC的周长=DB+BC+CD,
∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10.
故选C.
分析:由ED是AB的垂直平分线,可得AD=BD,又由△BDC的周长=DB+BC+CD,即可得△BDC的周长=AD+BC+CD=AC+BC.
2.如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )
A. 48° B. 36° C. 30° D. 24°
答案:A
解析:解:∵BD平分∠ABC,
∴∠DBC=∠ABD=24°,
∵∠A=60°,
∴∠ACB=180°-60°-24°×2=72°,
∵BC的中垂线交BC于点E,
∴BF=CF,∴∠FCB=24°,
∴∠ACF=72°-24°=48°,
故选:A.
分析:根据角平分线的性质可得∠DBC=∠ABD=24°,然后再计算出∠ACB的度数,再根据线段垂直平分线的性质可得BF=CF,进而可得∠FCB=24°,然后可算出∠ACF的度数.
3.如图,在等腰△ABC中,一腰AB的垂直平分线交另一腰AC于点G,若已知AB=10,△GBC的周长为17,则底BC的长为( )
A. 10 B. 9 C. 7 D. 5
答案:C
解析:解:如图,∵在等腰△ABC中,一腰AB的垂直平分线交另一腰AC于点G,
∴AG=BG,
∵AB=10,△GBC的周长为17,
∴CG+BG+BC=CG+AG+BC=AC+BC=17,AC=AB=10,
∴BC=7.
故选C.
分析:首先根据题意在等腰△ABC中,一腰AB的垂直平分线交另一腰AC于点G,根据线段垂直平分线的性质,可得AG=BG,继而可得△GBC的周长=AC+BC=17,则可求得答案.
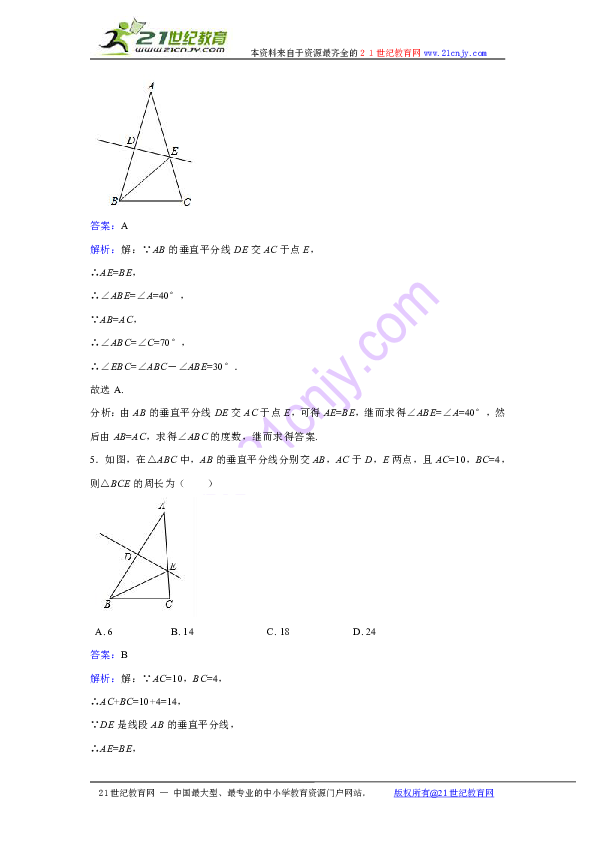
4.如图,AB=AC,∠A=40°,AB的垂直平分线DE交AC于点E,垂足为D,则∠EBC的度数是( )
A. 30° B. 40° C. 70° D. 80°
答案:A
解析:解:∵AB的垂直平分线DE交AC于点E,
∴AE=BE,
∴∠ABE=∠A=40°,
∵AB=AC,
∴∠ABC=∠C=70°,
∴∠EBC=∠ABC-∠ABE=30°.
故选A.
分析:由AB的垂直平分线DE交AC于点E,可得AE=BE,继而求得∠ABE=∠A=40°,然后由AB=AC,求得∠ABC的度数,继而求得答案.
5.如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,且AC=10,BC=4,则△BCE的周长为( )
A. 6 B. 14 C. 18 D. 24
答案:B
解析:解:∵AC=10,BC=4,
∴AC+BC=10+4=14,
∵DE是线段AB的垂直平分线,
∴AE=BE,
∴△BCE的周长=(BE+CE)+BC=AC+BC=14.
故选B.
分析:先根据AC=10,BC=4,可得出AC+BC的长,再根据DE是线段AB的垂直平分线可得到AE=BE,进而可得出答案.
6.如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
A. 18 B. 16 C. 17 D. 无法确定
答案:C
解析:解:在Rt△ABC中,∠C=90°,AC=12,AB=13,
由勾股定理得,BC=5,
∵MN是AB的垂直平分线,
∴MB=MA,
∴△BCM的周长=BC+CM+MB=BC+CM+MA=BC+CA=17,
故选:C
分析:根据勾股定理求出BC的长,根据线段垂直平分线的性质得到MB=MA,根据三角形的周长的计算方法代入计算即可.
7.如果三角形三条边的中垂线的交点在三角形的外部,那么,这个三角形是( )
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 等边三角形
答案:C
解析:解:如图,O是边AB和边AC的垂直平分线的交点,
则AO=OB,AO=OC,
所以∠OAB=∠OBA,∠OAC=∠OCA,
∵∠BAC=∠OAB+∠OAC=∠OBA+∠OCA,
∴∠BAC>∠ABC+∠ACB,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠BAC>90°,
即△ABC是钝角三角形,
故选C
分析:先根据题意画出图形,再根据线段垂直平分线性质、等腰三角形的性质、三角形的内角和定理求出∠BAC>90°即可.
8. 已知MN是线段AB的垂直平分线,C,D是MN上任意两点,则∠CAD和∠CBD之间的大小关系是( )
A.∠CAD<∠CBD B.∠CAD=∠CBD C.∠CAD>∠CBD D.无法确定
答案:B
解析:
解:∵MN是线段AB的垂直平分线,C,D是MN上任意两点,
∴AC=BC,AD=BD,
∴∠DAB=∠CBA,∠DAB=∠DBA,
如图1,∠CAD=∠CAB+∠DAB,∠CBD=∠CBA+∠DBA,
∴∠CAD=∠CBD;
如图2,∠CAD=∠CAB-∠DAB,∠CBD=∠CBA-∠DBA,
∴∠CAD=∠CBD.
故选B.
分析:首先根据题意画出图形,然后由MN是线段AB的垂直平分线,C,D是MN上任意两点,根据线段垂直平分线的性质可得:AC=BC,AD=BD,则可证得∠DAB=∠CBA,
∠DAB=∠DBA,继而求得答案.
9. 已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60 cm和38 cm,则△ABC的腰和底边长分别为( )
A.24 cm和12 cm B.16 cm和22 cm C.20 cm和16 cm D.22 cm和16 cm
答案:D
解析:
解:如图,连接BD,
∵D在线段AB的垂直平分线上,
∴BD=AD,
∴BD+DC+BC=AC+BC=38 cm,且AB+AC+BC=60 cm,
∴AB=60 cm-38 cm =22 cm,
∴AC=22 cm,
∴BC=38 cm-AC=38 cm-22 cm =16 cm,
即等腰三角形的腰为22 cm,底为16 cm,
故选D.
分析:连接BD,根据线段垂直平分线的性质可得到BD=AD,可知两三角形周长差为AB,结合条件可求得腰长,再由周长可求得BC,可得出答案.
10.如图,地面上有三个洞口A、B、C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口(到A、B、C三个点的距离相等),尽快抓到老鼠,应该蹲守在( )
A.△ABC三边垂直平分线的交点 B.△ABC三条角平分线的交点
C.△ABC三条高所在直线的交点 D.△ABC三条中线的交点
答案:A
解析:解:∵三角形三边垂直平分线的交点到三个顶点的距离相等,
∴猫应该蹲守在△ABC三边垂直平分线的交点处.
故选A
分析:根据题意,知猫应该到三个洞口的距离相等,则此点就是三角形三边垂直平分线的交点.
11. 三角形内有一点到三角形三顶点的距离相等,则这点一定是三角形的( )
A.三条中线的交点 B.三边垂直平分线的交点
C.三条高的交点 D.三条角平分线的交点
答案:B
解析:解:三角形内有一点到三角形三顶点的距离相等,则这点一定是三角形的三边垂直平分线的交点,
故选:B.
分析:根据线段垂直平分线的性质:线段垂直平分线上任意一点,到线段两端点的距离相等可得答案.
12. △ABC中,AB=AC,AB的垂直平分线与直线AC相交所成锐角为40°,则此等腰三角形的顶角为( )
A.50° B.60° C.150° D.50°或130°
答案:D
解析:解:(1)当AB的中垂线MN与AC相交时
易得∠A=90°-40°=50°,
(2)当AB的中垂线MN与CA的延长线相交时,
易得∠DAB=90°-40°=50°,
∴∠A=130°,
故选D.
分析:此题根据△ABC中∠A为锐角与钝角分为两种情况解答.
13. 如图,在Rt△ABC中,∠C=90°,直线DE是斜边AB的垂直平分线交AC于D.若AC=8,BC=6,则△DBC的周长为( )
A.12 B.14 C.16 D.无法计算
答案:B
解析:解:∵DE是AB的垂直平分线,
∴DA=DB,
∴△DBC的周长为CB+CD+DB=CB+CD+DA=BC+CA=6+8=14,
故选:B
分析:根据线段的垂直平分线上的点到线段的两个端点的距离相等得到DA=DB,根据三角形周长公式求出周长.
14. 如图,在△ABC中,AB=A,AC=B,BC边上的垂直平分线DE交BC、BA分别于点D、E,则△AEC的周长等于( )
A.A+B B.A-B C.2A+B D.A+2B
答案:A
解析:解:∵ED垂直且平分BC,
∴BE=CE.
∵AB=A,AC=B,
∴AB=AE+BE=AE+CE=A.
∴△AEC的周长为:AE+EC+AC=A+B.
故选A
分析:要求三角形的周长,知道AC=B,只要求得AE+EC即可,由DE是BC的垂直平分线,结合线段的垂直平分线的性质,知EC=BE,这样三角形周长的一部分AE+EC=AE+BE=AB,代入数值,答案可得.
15. 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.在AC,BC两边高线的交点处 B.在AC,BC两边中线的交点处
C.在AC,BC两边垂直平分线的交点处 D.在∠A,∠B两内角平分线的交点处
答案:C
解析:解:根据线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等.则超市应建在AC,BC两边垂直平分线的交点处.
故选C.
分析:要求到三小区的距离相等,首先思考到A小区、B小区距离相等,根据线段垂直平分线定理的逆定理知满足条件的点在线段AB的垂直平分线上,同理到B小区、C小区的距离相等的点在线段BC的垂直平分线上,于是到三个小区的距离相等的点应是其交点,答案可得.
二、填空题
16.△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于E,交BC于F.若FC=3 cm,则BF=_________.
答案:6 cm
解析:
解:连接AF.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°;
∵AC的垂直平分线EF交AC于点E,交BC于点F,
∴CF=AF,∠FAC=30°,
∴∠BAF=90°,
∴BF=2AF(30°直角边等于斜边的一半),
∴BF=2CF=6 cm.
故答案是:6 cm
分析:利用辅助线,连接AF,求出CF=AF,∠BAF=90°,再根据AB=AC,∠BAC=
120°可求出∠B的度数,由直角三角形的性质即可求出BF=2AF=2CF=6 cm.
17. 如图,ED为△ABC的AC边的垂直平分线,且AB=5,△BCE的周长为8,则BC=________.
答案:3
解析:解:∵ED为AC上的垂直平分线,
∴AE=EC,
∵AB=AE+EB=5,△BCE的周长=AE+BE+BC=AB+BC=8,
∴BC=8-5=3.
故答案为:3
分析:根据ED为AC上的垂直平分线,得出AE=CE,再根据AB=5,△BCE的周长为AB+BC=8,即可求得BC.
18.如图,已知在△ABC中,AB=AC=10,DE垂直平分AB,垂足为E,DE交AC于D,若△BDC的周长为16,则BC=__________ .
答案:6
解析:解:∵DE垂直平分AB,
∴AD=BD,
∴AD+CD=BD+CD,即AC=BD+CD,
∵AC=10,△BDC的周长为16,
∴BC=16-AC=16-10=6.
故答案为:6
分析:先根据DE垂直平分AB可知,AD=BD,即AC=BD+CD,再由AC=10,△BDC的周长为16即可求出答案.
19. 如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,已知∠ADE=40°,则∠DBC=
答案:15
解析:解:∵DE垂直平分AB,
∴AD=BD,∠AED=90°,
∴∠A=∠ABD,
∵∠ADE=40°,
∴∠A=90°-40°=50°,
∴∠ABD=∠A=50°,
∵AB=AC,
∴∠ABC=∠C=65°,
∴∠DBC=∠ABC-∠ABD=65°-50°=15°,
故答案为:15
分析:根据线段垂直平分线求出AD=BD,推出∠A=∠ABD=50°,根据三角形内角和定理和等腰三角形性质求出∠ABC,即可得出答案.
20. 点P在线段AB的垂直平分线上,PA=7,则PB= _________.
答案:7
解析:解:∵点P在线段AB的垂直平分线上,PA=7,
∴PB=PA=7,
故答案为:7
分析:根据线段垂直平分线的性质得出PA=PB,代入即可求出答案.
三、解答题
21. 某公园有海盗船、摩天轮、碰碰车三个娱乐项目,现要在公园内建一个售票中心,使
三个娱乐项目所处位置到售票中心的距离相等,请在图中确定售票中心的位置.
答案:解:如图,①连接AB,AC,
②分别作线段AB,AC的垂直平分线,两垂直平分线相较于点P,
则P即为售票中心
解析:由三个娱乐项目所处位置到售票中心的距离相等,可得售票中心是海盗船、摩天轮、碰碰车三个娱乐场组成三角形的三边的垂直平分线的交点.
22.如图,在△ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于D,E.若∠CAE=∠B+30°,求∠AEB的度数
答案:140°
解析:解:∵DE垂直平分AB,
∴AE=BE,
∴∠B=∠EAB.
∵∠C=90°,∠CAE=∠B+30°,
∴∠B+30°+∠B+∠B=90°,
∴∠B=20°,
∴∠AEB=180°-20°-20°=140°.
分析:根据线段垂直平分线求出AE=BE,推出∠B=∠EAB,根据已知和三角形内角和定理得出∠B+30°+∠B+∠B=90°,求出∠B,即可得出答案.
23.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长
答案:(1)证明:∵AB的垂直平分线MN交AC于点D,∴DB=DA,
∴△ABD是等腰三角形.
(2)30°(3)32
解析:解:(1)证明:∵AB的垂直平分线MN交AC于点D,
∴DB=DA,
∴△ABD是等腰三角形;
(2)∵△ABD是等腰三角形,∠A=40°,
∴∠ABD=∠A=40°,∠ABC=∠C=(180°-40°)÷2=70°.
∴∠BDC=∠ABC-∠ABD=70°-40°=30°.
(3)∵AB的垂直平分线MN交AC于点D,AE=6,
∴AB=2AD=12.
∵△CBD的周长为20,
∴AC+BC=20,
∴△ABC的周长=AB+AC+BC=12+20=32.
分析:(1)根据线段的垂直平分线到线段两端点的距离相等即可得证;
(2)首先利用三角形内角和求得∠ABC的度数,然后减去∠ABD的度数即可得到答案;
(3)将△ABC的周长转化为AB+AC+BC的长即可求得.
24.如图所示,在△ABC中,DE是边AB的垂直平分线,交AB于E,交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=50°,求∠DBC的度数.
(2)若AB=AC,且△BCD的周长为18 cm,△ABC的周长为30 cm,求BE的长.
答案:(1)15°;(2)6 cm
解析:解:(1)∵∠A=50°,
∴∠ABC=∠C=65°.
又∵DE垂直平分AB,
∴∠A=∠ABD=50°,
∴∠DBC=∠ABC-∠ABD=15°.
(2)∵DE是AB的垂直平分线,
∴AD=BD,AE=BE,
∴△BCD的周长=BC+CD+BD=BC+CD+AD=BC+AC=18 cm.
∵△ABC的周长=30 cm,
∴AB=30-18=12 cm,
∴BE=AE=6 cm.
分析:(1)已知∠A=50°,易求∠ABC的度数.又因为DE垂直平分AB根据线段垂直平分线的性质易求出∠DBC的度数.
(2)同样利用线段垂直平分线的性质:垂直平分线上任意一点,和线段两端点的距离相等可解.
25.已知:如图,在△ABC中,MN是边AB的中垂线,∠MAC=50°,∠C=3∠B,求∠B的度数
答案:=26°
解析:解:∵MN是边AB的中垂线,
∴AM=BM,
∴∠BAM=∠B.
设∠B=x,则∠BAM=x,
∵∠C=3∠B,∴∠C=3x,
在△ABC中,由三角形内角和定理,得x+x+3x+50°=180°,
∴x=26°,
即∠B=26°
分析:根据线段垂直平分线性质得出AM=BM,推出∠BAM=∠B,设∠B=x,则∠BAM=x,∠C=3x,在△ABC中,由三角形内角和定理得出方程x+x+3x+50°=180°,求出即可
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
北师大版数学八年级下册1.3线段的垂直平分线课时练习
一、选择题
1.如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是( )
A. 8 B. 9 C. 10 D.11
答案:C
解析:解:∵ED是AB的垂直平分线,
∴AD=BD,
∵△BDC的周长=DB+BC+CD,
∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10.
故选C.
分析:由ED是AB的垂直平分线,可得AD=BD,又由△BDC的周长=DB+BC+CD,即可得△BDC的周长=AD+BC+CD=AC+BC.
2.如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )
A. 48° B. 36° C. 30° D. 24°
答案:A
解析:解:∵BD平分∠ABC,
∴∠DBC=∠ABD=24°,
∵∠A=60°,
∴∠ACB=180°-60°-24°×2=72°,
∵BC的中垂线交BC于点E,
∴BF=CF,∴∠FCB=24°,
∴∠ACF=72°-24°=48°,
故选:A.
分析:根据角平分线的性质可得∠DBC=∠ABD=24°,然后再计算出∠ACB的度数,再根据线段垂直平分线的性质可得BF=CF,进而可得∠FCB=24°,然后可算出∠ACF的度数.
3.如图,在等腰△ABC中,一腰AB的垂直平分线交另一腰AC于点G,若已知AB=10,△GBC的周长为17,则底BC的长为( )
A. 10 B. 9 C. 7 D. 5
答案:C
解析:解:如图,∵在等腰△ABC中,一腰AB的垂直平分线交另一腰AC于点G,
∴AG=BG,
∵AB=10,△GBC的周长为17,
∴CG+BG+BC=CG+AG+BC=AC+BC=17,AC=AB=10,
∴BC=7.
故选C.
分析:首先根据题意在等腰△ABC中,一腰AB的垂直平分线交另一腰AC于点G,根据线段垂直平分线的性质,可得AG=BG,继而可得△GBC的周长=AC+BC=17,则可求得答案.
4.如图,AB=AC,∠A=40°,AB的垂直平分线DE交AC于点E,垂足为D,则∠EBC的度数是( )
A. 30° B. 40° C. 70° D. 80°
答案:A
解析:解:∵AB的垂直平分线DE交AC于点E,
∴AE=BE,
∴∠ABE=∠A=40°,
∵AB=AC,
∴∠ABC=∠C=70°,
∴∠EBC=∠ABC-∠ABE=30°.
故选A.
分析:由AB的垂直平分线DE交AC于点E,可得AE=BE,继而求得∠ABE=∠A=40°,然后由AB=AC,求得∠ABC的度数,继而求得答案.
5.如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,且AC=10,BC=4,则△BCE的周长为( )
A. 6 B. 14 C. 18 D. 24
答案:B
解析:解:∵AC=10,BC=4,
∴AC+BC=10+4=14,
∵DE是线段AB的垂直平分线,
∴AE=BE,
∴△BCE的周长=(BE+CE)+BC=AC+BC=14.
故选B.
分析:先根据AC=10,BC=4,可得出AC+BC的长,再根据DE是线段AB的垂直平分线可得到AE=BE,进而可得出答案.
6.如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
A. 18 B. 16 C. 17 D. 无法确定
答案:C
解析:解:在Rt△ABC中,∠C=90°,AC=12,AB=13,
由勾股定理得,BC=5,
∵MN是AB的垂直平分线,
∴MB=MA,
∴△BCM的周长=BC+CM+MB=BC+CM+MA=BC+CA=17,
故选:C
分析:根据勾股定理求出BC的长,根据线段垂直平分线的性质得到MB=MA,根据三角形的周长的计算方法代入计算即可.
7.如果三角形三条边的中垂线的交点在三角形的外部,那么,这个三角形是( )
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 等边三角形
答案:C
解析:解:如图,O是边AB和边AC的垂直平分线的交点,
则AO=OB,AO=OC,
所以∠OAB=∠OBA,∠OAC=∠OCA,
∵∠BAC=∠OAB+∠OAC=∠OBA+∠OCA,
∴∠BAC>∠ABC+∠ACB,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠BAC>90°,
即△ABC是钝角三角形,
故选C
分析:先根据题意画出图形,再根据线段垂直平分线性质、等腰三角形的性质、三角形的内角和定理求出∠BAC>90°即可.
8. 已知MN是线段AB的垂直平分线,C,D是MN上任意两点,则∠CAD和∠CBD之间的大小关系是( )
A.∠CAD<∠CBD B.∠CAD=∠CBD C.∠CAD>∠CBD D.无法确定
答案:B
解析:
解:∵MN是线段AB的垂直平分线,C,D是MN上任意两点,
∴AC=BC,AD=BD,
∴∠DAB=∠CBA,∠DAB=∠DBA,
如图1,∠CAD=∠CAB+∠DAB,∠CBD=∠CBA+∠DBA,
∴∠CAD=∠CBD;
如图2,∠CAD=∠CAB-∠DAB,∠CBD=∠CBA-∠DBA,
∴∠CAD=∠CBD.
故选B.
分析:首先根据题意画出图形,然后由MN是线段AB的垂直平分线,C,D是MN上任意两点,根据线段垂直平分线的性质可得:AC=BC,AD=BD,则可证得∠DAB=∠CBA,
∠DAB=∠DBA,继而求得答案.
9. 已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60 cm和38 cm,则△ABC的腰和底边长分别为( )
A.24 cm和12 cm B.16 cm和22 cm C.20 cm和16 cm D.22 cm和16 cm
答案:D
解析:
解:如图,连接BD,
∵D在线段AB的垂直平分线上,
∴BD=AD,
∴BD+DC+BC=AC+BC=38 cm,且AB+AC+BC=60 cm,
∴AB=60 cm-38 cm =22 cm,
∴AC=22 cm,
∴BC=38 cm-AC=38 cm-22 cm =16 cm,
即等腰三角形的腰为22 cm,底为16 cm,
故选D.
分析:连接BD,根据线段垂直平分线的性质可得到BD=AD,可知两三角形周长差为AB,结合条件可求得腰长,再由周长可求得BC,可得出答案.
10.如图,地面上有三个洞口A、B、C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口(到A、B、C三个点的距离相等),尽快抓到老鼠,应该蹲守在( )
A.△ABC三边垂直平分线的交点 B.△ABC三条角平分线的交点
C.△ABC三条高所在直线的交点 D.△ABC三条中线的交点
答案:A
解析:解:∵三角形三边垂直平分线的交点到三个顶点的距离相等,
∴猫应该蹲守在△ABC三边垂直平分线的交点处.
故选A
分析:根据题意,知猫应该到三个洞口的距离相等,则此点就是三角形三边垂直平分线的交点.
11. 三角形内有一点到三角形三顶点的距离相等,则这点一定是三角形的( )
A.三条中线的交点 B.三边垂直平分线的交点
C.三条高的交点 D.三条角平分线的交点
答案:B
解析:解:三角形内有一点到三角形三顶点的距离相等,则这点一定是三角形的三边垂直平分线的交点,
故选:B.
分析:根据线段垂直平分线的性质:线段垂直平分线上任意一点,到线段两端点的距离相等可得答案.
12. △ABC中,AB=AC,AB的垂直平分线与直线AC相交所成锐角为40°,则此等腰三角形的顶角为( )
A.50° B.60° C.150° D.50°或130°
答案:D
解析:解:(1)当AB的中垂线MN与AC相交时
易得∠A=90°-40°=50°,
(2)当AB的中垂线MN与CA的延长线相交时,
易得∠DAB=90°-40°=50°,
∴∠A=130°,
故选D.
分析:此题根据△ABC中∠A为锐角与钝角分为两种情况解答.
13. 如图,在Rt△ABC中,∠C=90°,直线DE是斜边AB的垂直平分线交AC于D.若AC=8,BC=6,则△DBC的周长为( )
A.12 B.14 C.16 D.无法计算
答案:B
解析:解:∵DE是AB的垂直平分线,
∴DA=DB,
∴△DBC的周长为CB+CD+DB=CB+CD+DA=BC+CA=6+8=14,
故选:B
分析:根据线段的垂直平分线上的点到线段的两个端点的距离相等得到DA=DB,根据三角形周长公式求出周长.
14. 如图,在△ABC中,AB=A,AC=B,BC边上的垂直平分线DE交BC、BA分别于点D、E,则△AEC的周长等于( )
A.A+B B.A-B C.2A+B D.A+2B
答案:A
解析:解:∵ED垂直且平分BC,
∴BE=CE.
∵AB=A,AC=B,
∴AB=AE+BE=AE+CE=A.
∴△AEC的周长为:AE+EC+AC=A+B.
故选A
分析:要求三角形的周长,知道AC=B,只要求得AE+EC即可,由DE是BC的垂直平分线,结合线段的垂直平分线的性质,知EC=BE,这样三角形周长的一部分AE+EC=AE+BE=AB,代入数值,答案可得.
15. 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.在AC,BC两边高线的交点处 B.在AC,BC两边中线的交点处
C.在AC,BC两边垂直平分线的交点处 D.在∠A,∠B两内角平分线的交点处
答案:C
解析:解:根据线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等.则超市应建在AC,BC两边垂直平分线的交点处.
故选C.
分析:要求到三小区的距离相等,首先思考到A小区、B小区距离相等,根据线段垂直平分线定理的逆定理知满足条件的点在线段AB的垂直平分线上,同理到B小区、C小区的距离相等的点在线段BC的垂直平分线上,于是到三个小区的距离相等的点应是其交点,答案可得.
二、填空题
16.△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于E,交BC于F.若FC=3 cm,则BF=_________.
答案:6 cm
解析:
解:连接AF.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°;
∵AC的垂直平分线EF交AC于点E,交BC于点F,
∴CF=AF,∠FAC=30°,
∴∠BAF=90°,
∴BF=2AF(30°直角边等于斜边的一半),
∴BF=2CF=6 cm.
故答案是:6 cm
分析:利用辅助线,连接AF,求出CF=AF,∠BAF=90°,再根据AB=AC,∠BAC=
120°可求出∠B的度数,由直角三角形的性质即可求出BF=2AF=2CF=6 cm.
17. 如图,ED为△ABC的AC边的垂直平分线,且AB=5,△BCE的周长为8,则BC=________.
答案:3
解析:解:∵ED为AC上的垂直平分线,
∴AE=EC,
∵AB=AE+EB=5,△BCE的周长=AE+BE+BC=AB+BC=8,
∴BC=8-5=3.
故答案为:3
分析:根据ED为AC上的垂直平分线,得出AE=CE,再根据AB=5,△BCE的周长为AB+BC=8,即可求得BC.
18.如图,已知在△ABC中,AB=AC=10,DE垂直平分AB,垂足为E,DE交AC于D,若△BDC的周长为16,则BC=__________ .
答案:6
解析:解:∵DE垂直平分AB,
∴AD=BD,
∴AD+CD=BD+CD,即AC=BD+CD,
∵AC=10,△BDC的周长为16,
∴BC=16-AC=16-10=6.
故答案为:6
分析:先根据DE垂直平分AB可知,AD=BD,即AC=BD+CD,再由AC=10,△BDC的周长为16即可求出答案.
19. 如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,已知∠ADE=40°,则∠DBC=
答案:15
解析:解:∵DE垂直平分AB,
∴AD=BD,∠AED=90°,
∴∠A=∠ABD,
∵∠ADE=40°,
∴∠A=90°-40°=50°,
∴∠ABD=∠A=50°,
∵AB=AC,
∴∠ABC=∠C=65°,
∴∠DBC=∠ABC-∠ABD=65°-50°=15°,
故答案为:15
分析:根据线段垂直平分线求出AD=BD,推出∠A=∠ABD=50°,根据三角形内角和定理和等腰三角形性质求出∠ABC,即可得出答案.
20. 点P在线段AB的垂直平分线上,PA=7,则PB= _________.
答案:7
解析:解:∵点P在线段AB的垂直平分线上,PA=7,
∴PB=PA=7,
故答案为:7
分析:根据线段垂直平分线的性质得出PA=PB,代入即可求出答案.
三、解答题
21. 某公园有海盗船、摩天轮、碰碰车三个娱乐项目,现要在公园内建一个售票中心,使
三个娱乐项目所处位置到售票中心的距离相等,请在图中确定售票中心的位置.
答案:解:如图,①连接AB,AC,
②分别作线段AB,AC的垂直平分线,两垂直平分线相较于点P,
则P即为售票中心
解析:由三个娱乐项目所处位置到售票中心的距离相等,可得售票中心是海盗船、摩天轮、碰碰车三个娱乐场组成三角形的三边的垂直平分线的交点.
22.如图,在△ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于D,E.若∠CAE=∠B+30°,求∠AEB的度数
答案:140°
解析:解:∵DE垂直平分AB,
∴AE=BE,
∴∠B=∠EAB.
∵∠C=90°,∠CAE=∠B+30°,
∴∠B+30°+∠B+∠B=90°,
∴∠B=20°,
∴∠AEB=180°-20°-20°=140°.
分析:根据线段垂直平分线求出AE=BE,推出∠B=∠EAB,根据已知和三角形内角和定理得出∠B+30°+∠B+∠B=90°,求出∠B,即可得出答案.
23.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长
答案:(1)证明:∵AB的垂直平分线MN交AC于点D,∴DB=DA,
∴△ABD是等腰三角形.
(2)30°(3)32
解析:解:(1)证明:∵AB的垂直平分线MN交AC于点D,
∴DB=DA,
∴△ABD是等腰三角形;
(2)∵△ABD是等腰三角形,∠A=40°,
∴∠ABD=∠A=40°,∠ABC=∠C=(180°-40°)÷2=70°.
∴∠BDC=∠ABC-∠ABD=70°-40°=30°.
(3)∵AB的垂直平分线MN交AC于点D,AE=6,
∴AB=2AD=12.
∵△CBD的周长为20,
∴AC+BC=20,
∴△ABC的周长=AB+AC+BC=12+20=32.
分析:(1)根据线段的垂直平分线到线段两端点的距离相等即可得证;
(2)首先利用三角形内角和求得∠ABC的度数,然后减去∠ABD的度数即可得到答案;
(3)将△ABC的周长转化为AB+AC+BC的长即可求得.
24.如图所示,在△ABC中,DE是边AB的垂直平分线,交AB于E,交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=50°,求∠DBC的度数.
(2)若AB=AC,且△BCD的周长为18 cm,△ABC的周长为30 cm,求BE的长.
答案:(1)15°;(2)6 cm
解析:解:(1)∵∠A=50°,
∴∠ABC=∠C=65°.
又∵DE垂直平分AB,
∴∠A=∠ABD=50°,
∴∠DBC=∠ABC-∠ABD=15°.
(2)∵DE是AB的垂直平分线,
∴AD=BD,AE=BE,
∴△BCD的周长=BC+CD+BD=BC+CD+AD=BC+AC=18 cm.
∵△ABC的周长=30 cm,
∴AB=30-18=12 cm,
∴BE=AE=6 cm.
分析:(1)已知∠A=50°,易求∠ABC的度数.又因为DE垂直平分AB根据线段垂直平分线的性质易求出∠DBC的度数.
(2)同样利用线段垂直平分线的性质:垂直平分线上任意一点,和线段两端点的距离相等可解.
25.已知:如图,在△ABC中,MN是边AB的中垂线,∠MAC=50°,∠C=3∠B,求∠B的度数
答案:=26°
解析:解:∵MN是边AB的中垂线,
∴AM=BM,
∴∠BAM=∠B.
设∠B=x,则∠BAM=x,
∵∠C=3∠B,∴∠C=3x,
在△ABC中,由三角形内角和定理,得x+x+3x+50°=180°,
∴x=26°,
即∠B=26°
分析:根据线段垂直平分线性质得出AM=BM,推出∠BAM=∠B,设∠B=x,则∠BAM=x,∠C=3x,在△ABC中,由三角形内角和定理得出方程x+x+3x+50°=180°,求出即可
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
