2024-2025北师大八年级下数学 第三章 图形的平移与旋转 测试卷(含答案)
文档属性
| 名称 | 2024-2025北师大八年级下数学 第三章 图形的平移与旋转 测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 241.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 00:00:00 | ||
图片预览


文档简介
第三章图形的平移与旋转测试卷
(时间:120分钟 满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案
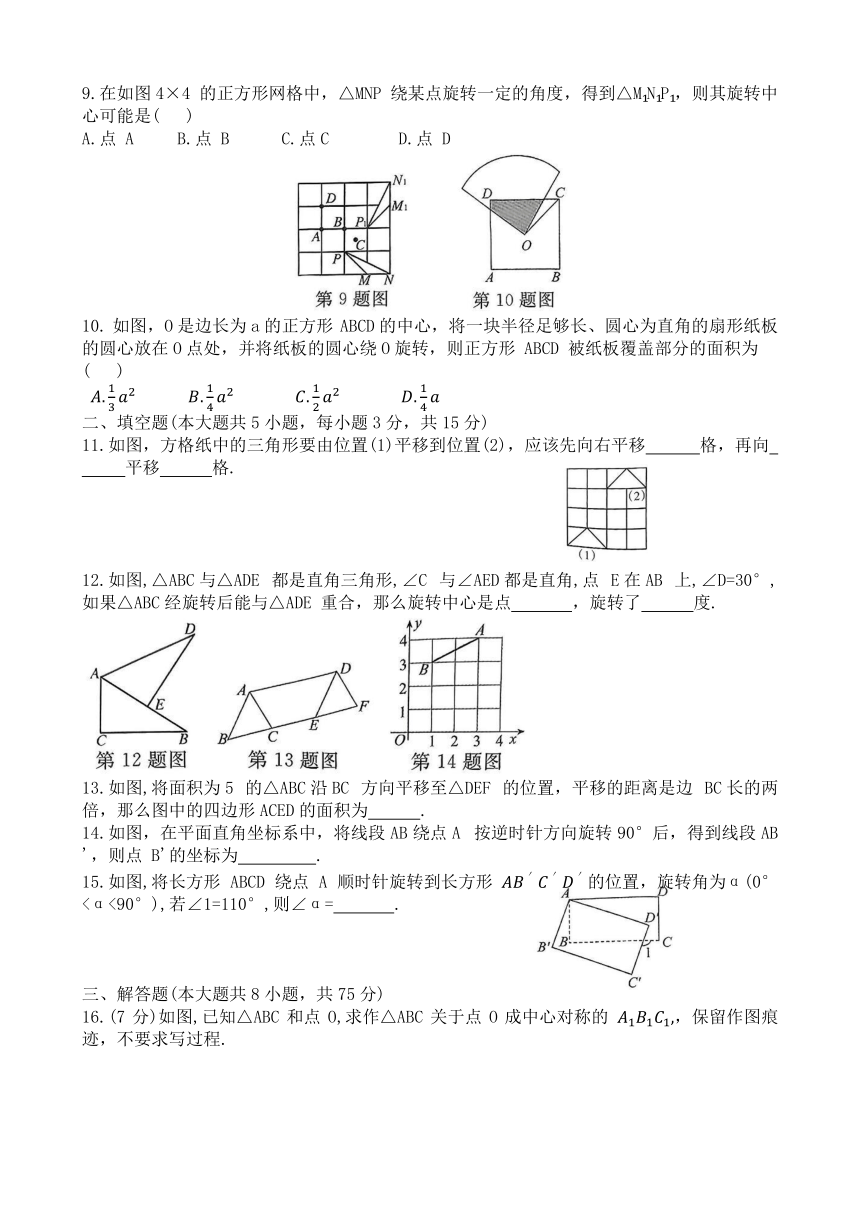
1.在下列图形中,既是轴对称图形又是中心对称图形的是 ( )
2.一个图形无论经过平移变换,还是经过旋转变换,下列说法正确的是 ( )
①对应线段平行;②对应线段相等;③图形的形状和大小都没有发生变化;④对应角相等.
A.①②③ B.②③④ C.①②④ D.①③④
封3.如图,△ABC和△BDE 是等边三角形,点 A、B、D 在一条直线上,并且AB=BD.由一个三角形变换到另一个三角形 ( )
A.仅能由平移得到
B.仅能由旋转得到
C.既能由平移得到,也能由旋转得到
D.既不能由平移得到,也不能由旋转得到
4.将点A(3,2)沿x轴向左平移4个单位长度得到点 A',点A'关于y轴对称的点的坐标是( )
A.(-3,2) B.(-1,2) C.(1,2) D.(1,-2)
5.如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C 的位置,使得点C、A、B 在同一条直线上,那么旋转角等于( )
A.55° B.70° C.125° D.145°
6.如图,在 中, ,在同一平面内,将 绕点A 旋转到的位置,使得C∥AB则 ( )
A.30°
7.在平面直角坐标系中,线段OP 的两个端点坐标分别是O(0,0),P(4,3),将线段OP绕点O 逆时针旋转到 位置,则点 P'的坐标为 ( )
A.(3,4) B.(-4,3) C.(-3,4) D.(4,-3)
8.如图,Rt△ABC 沿直角边 BC 所在的直线向右平移得到△DEF,下列结论中错误的是( )
A.△ABC≌△DEF B.∠DEF=90°
C. AC=DF D. EC=CF
9.在如图4×4 的正方形网格中,△MNP 绕某点旋转一定的角度,得到△M N P ,则其旋转中心可能是( )
A.点 A B.点 B C.点C D.点 D
如图,O是边长为a的正方形 ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形 ABCD 被纸板覆盖部分的面积为
( )
二、填空题(本大题共5小题,每小题3分,共15分)
11.如图,方格纸中的三角形要由位置(1)平移到位置(2),应该先向右平移 格,再向 平移 格.
12.如图,△ABC与△ADE 都是直角三角形,∠C 与∠AED都是直角,点 E在AB 上,∠D=30°,如果△ABC经旋转后能与△ADE 重合,那么旋转中心是点 ,旋转了 度.
13.如图,将面积为5 的△ABC沿BC 方向平移至△DEF 的位置,平移的距离是边 BC长的两倍,那么图中的四边形ACED的面积为 .
14.如图,在平面直角坐标系中,将线段AB绕点A 按逆时针方向旋转90°后,得到线段AB',则点 B'的坐标为 .
15.如图,将长方形 ABCD 绕点 A 顺时针旋转到长方形 的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α= .
三、解答题(本大题共8小题,共75分)
16.(7分)如图,已知△ABC和点O,求作△ABC关于点O成中心对称的 ,保留作图痕迹,不要求写过程.
17.(9 分)如图,将△ABC 绕点 C 顺时针方向旋转 40°得 若,求∠BAC的度数.
18.(9分)如图,直角△ABC的周长为18,在其内部有5个小直角三角形,同一方向直角边都互相平行,求这5个小直角三角形的周长之和.
C
19.(9分)如图,△ABC是等腰三角形,∠ACB=90°,点 D 是AB 的中点,试作出△ABC 绕点 D 顺时针旋转 90°所得的图形,并指出图形中有多少个等腰直角三角形
B
20.(9分)如图,在 Rt△ABC中,∠ACB=90°,点 D、F 分别在AB、AC上,CF=CB,连接CD,将线段 CD 绕点C 按顺时针方向旋转 90°后得CE,连接 EF.
(1)求证:△BCD≌△FCE;
(2)若 EF∥CD,求∠BDC 的度数.
21.(10分)如图,方格纸中每个小正方形的边长都是1个单位长度, 的三个顶点A(--2,2),B(0,5),C(0,2).
(1)将 以点 C 为 旋转中心旋转 得到 请画出 的图形.
(2)平移 ,使点A的对应点. 坐标为请画出平移后对应的的图形.
(3)若将 绕某一点旋转可得到 请直接写出旋转中心的坐标.
22.(10分)利用对称变换可设计出美丽图案,如图是一个方格纸中每一个顶点都在格点上的四边形,且每个小正方形的边长都为1,完成下列问题:
(1)图案设计:先作出四边形关于直线l成轴对称的图形,再将你所作的图形和原四边形绕O点按顺时针旋转
(2)完成上述图案设计后,可知这个图案的面积等于 ,
23.(12分)已知, 为等边三角形,有一块含有角的直角三角形 DEF 如图放置,让等边. 在EF 所在的直线上向右平移.
(1)如图1,当点E与点 B 重合时,点A 恰好落在三角形斜边DF上,试证明:
(2)在三角形ABC的平移过程中,设AB,AC与三角形斜边的交点分别为G,H,试在图2中探究是否始乡成立 若成立,请证明;若不成立,请说明理由.
第三章测试卷答案
1. D 2. B 3. C 4. C 5. C
6. A 7. C 8. D 9. B 10. B
11.2 上 3 12. A 60
13.15 14.(4,2) 15.20°
16.图略.
17.∵△ABC 绕点 C 顺时针方向旋转40°得△A'B'C',
∴∠BAC=50°.
18.利用平移的性质可得出,这五个小三角形的周长的和等于大三角形的周长为18.
19.图略,共有5 个等腰直角三角形:△ACD, △ABC, △BCD,△ACA',△A'AD.
20.(1)证明:∵将线段CD 绕点C 按顺时针方向旋转 90°后得CE,
∴CD = CE, ∠DCE = 90°, ∵∠ACB=90°,
∠FCE,
在△BCD和△FCE中,
∴△BCD≌△FCE(SAS);
(2)由(1)可知△BCD≌△FCE,∴∠BDC=∠E,∵EF∥CD,∴∠E=180°-∠DCE=90°,∴∠BDC=90°.
21.(1)图略;(2)图略;(3)旋转中心坐标为(0,-2).
22.(1)图略:
(2)面积:
23.(1)证明:∵△ABC 是等边三角形,
∴∠ACB=60°,AC=BC.
∵∠F=30°,
∴∠CAF=∠F,
∴CF=AC,
∴CF=AC=EC,
∴EF=2BC;
(2)成立.理由如下:
∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC.
∵∠F=30°,
∴∠CHF=∠F,
∴CH=CF.
∵EF=2BC,
∴BE+CF=BC.
∵AH+CH=AC,AC=BC,
∴AH=BE.
(时间:120分钟 满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案
1.在下列图形中,既是轴对称图形又是中心对称图形的是 ( )
2.一个图形无论经过平移变换,还是经过旋转变换,下列说法正确的是 ( )
①对应线段平行;②对应线段相等;③图形的形状和大小都没有发生变化;④对应角相等.
A.①②③ B.②③④ C.①②④ D.①③④
封3.如图,△ABC和△BDE 是等边三角形,点 A、B、D 在一条直线上,并且AB=BD.由一个三角形变换到另一个三角形 ( )
A.仅能由平移得到
B.仅能由旋转得到
C.既能由平移得到,也能由旋转得到
D.既不能由平移得到,也不能由旋转得到
4.将点A(3,2)沿x轴向左平移4个单位长度得到点 A',点A'关于y轴对称的点的坐标是( )
A.(-3,2) B.(-1,2) C.(1,2) D.(1,-2)
5.如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C 的位置,使得点C、A、B 在同一条直线上,那么旋转角等于( )
A.55° B.70° C.125° D.145°
6.如图,在 中, ,在同一平面内,将 绕点A 旋转到的位置,使得C∥AB则 ( )
A.30°
7.在平面直角坐标系中,线段OP 的两个端点坐标分别是O(0,0),P(4,3),将线段OP绕点O 逆时针旋转到 位置,则点 P'的坐标为 ( )
A.(3,4) B.(-4,3) C.(-3,4) D.(4,-3)
8.如图,Rt△ABC 沿直角边 BC 所在的直线向右平移得到△DEF,下列结论中错误的是( )
A.△ABC≌△DEF B.∠DEF=90°
C. AC=DF D. EC=CF
9.在如图4×4 的正方形网格中,△MNP 绕某点旋转一定的角度,得到△M N P ,则其旋转中心可能是( )
A.点 A B.点 B C.点C D.点 D
如图,O是边长为a的正方形 ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形 ABCD 被纸板覆盖部分的面积为
( )
二、填空题(本大题共5小题,每小题3分,共15分)
11.如图,方格纸中的三角形要由位置(1)平移到位置(2),应该先向右平移 格,再向 平移 格.
12.如图,△ABC与△ADE 都是直角三角形,∠C 与∠AED都是直角,点 E在AB 上,∠D=30°,如果△ABC经旋转后能与△ADE 重合,那么旋转中心是点 ,旋转了 度.
13.如图,将面积为5 的△ABC沿BC 方向平移至△DEF 的位置,平移的距离是边 BC长的两倍,那么图中的四边形ACED的面积为 .
14.如图,在平面直角坐标系中,将线段AB绕点A 按逆时针方向旋转90°后,得到线段AB',则点 B'的坐标为 .
15.如图,将长方形 ABCD 绕点 A 顺时针旋转到长方形 的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α= .
三、解答题(本大题共8小题,共75分)
16.(7分)如图,已知△ABC和点O,求作△ABC关于点O成中心对称的 ,保留作图痕迹,不要求写过程.
17.(9 分)如图,将△ABC 绕点 C 顺时针方向旋转 40°得 若,求∠BAC的度数.
18.(9分)如图,直角△ABC的周长为18,在其内部有5个小直角三角形,同一方向直角边都互相平行,求这5个小直角三角形的周长之和.
C
19.(9分)如图,△ABC是等腰三角形,∠ACB=90°,点 D 是AB 的中点,试作出△ABC 绕点 D 顺时针旋转 90°所得的图形,并指出图形中有多少个等腰直角三角形
B
20.(9分)如图,在 Rt△ABC中,∠ACB=90°,点 D、F 分别在AB、AC上,CF=CB,连接CD,将线段 CD 绕点C 按顺时针方向旋转 90°后得CE,连接 EF.
(1)求证:△BCD≌△FCE;
(2)若 EF∥CD,求∠BDC 的度数.
21.(10分)如图,方格纸中每个小正方形的边长都是1个单位长度, 的三个顶点A(--2,2),B(0,5),C(0,2).
(1)将 以点 C 为 旋转中心旋转 得到 请画出 的图形.
(2)平移 ,使点A的对应点. 坐标为请画出平移后对应的的图形.
(3)若将 绕某一点旋转可得到 请直接写出旋转中心的坐标.
22.(10分)利用对称变换可设计出美丽图案,如图是一个方格纸中每一个顶点都在格点上的四边形,且每个小正方形的边长都为1,完成下列问题:
(1)图案设计:先作出四边形关于直线l成轴对称的图形,再将你所作的图形和原四边形绕O点按顺时针旋转
(2)完成上述图案设计后,可知这个图案的面积等于 ,
23.(12分)已知, 为等边三角形,有一块含有角的直角三角形 DEF 如图放置,让等边. 在EF 所在的直线上向右平移.
(1)如图1,当点E与点 B 重合时,点A 恰好落在三角形斜边DF上,试证明:
(2)在三角形ABC的平移过程中,设AB,AC与三角形斜边的交点分别为G,H,试在图2中探究是否始乡成立 若成立,请证明;若不成立,请说明理由.
第三章测试卷答案
1. D 2. B 3. C 4. C 5. C
6. A 7. C 8. D 9. B 10. B
11.2 上 3 12. A 60
13.15 14.(4,2) 15.20°
16.图略.
17.∵△ABC 绕点 C 顺时针方向旋转40°得△A'B'C',
∴∠BAC=50°.
18.利用平移的性质可得出,这五个小三角形的周长的和等于大三角形的周长为18.
19.图略,共有5 个等腰直角三角形:△ACD, △ABC, △BCD,△ACA',△A'AD.
20.(1)证明:∵将线段CD 绕点C 按顺时针方向旋转 90°后得CE,
∴CD = CE, ∠DCE = 90°, ∵∠ACB=90°,
∠FCE,
在△BCD和△FCE中,
∴△BCD≌△FCE(SAS);
(2)由(1)可知△BCD≌△FCE,∴∠BDC=∠E,∵EF∥CD,∴∠E=180°-∠DCE=90°,∴∠BDC=90°.
21.(1)图略;(2)图略;(3)旋转中心坐标为(0,-2).
22.(1)图略:
(2)面积:
23.(1)证明:∵△ABC 是等边三角形,
∴∠ACB=60°,AC=BC.
∵∠F=30°,
∴∠CAF=∠F,
∴CF=AC,
∴CF=AC=EC,
∴EF=2BC;
(2)成立.理由如下:
∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC.
∵∠F=30°,
∴∠CHF=∠F,
∴CH=CF.
∵EF=2BC,
∴BE+CF=BC.
∵AH+CH=AC,AC=BC,
∴AH=BE.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
