18.2.1矩形的性质课件(16张ppt)
文档属性
| 名称 | 18.2.1矩形的性质课件(16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 854.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-11 20:54:52 | ||
图片预览

文档简介
课件16张PPT。18.2.1 矩形 学习目标 1.理解矩形的概念,明确矩形与平行四边形的区别与联系
2.探索并证明矩形的性质,会用矩形的性质解决相关问题
3.理解“直角三角形斜边上的中线等于斜边 的一半”这一重要结论对边平行
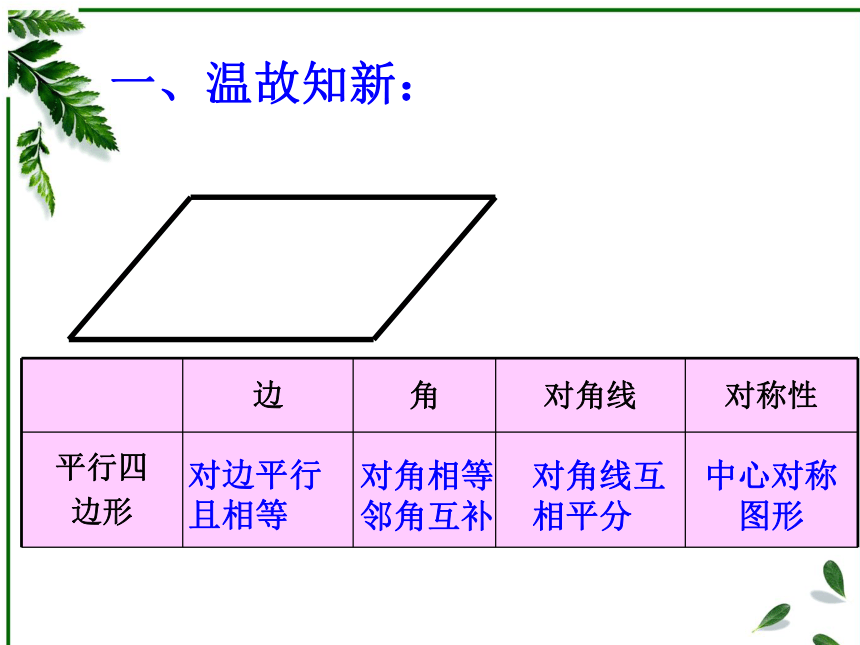
且相等对角相等
邻角互补对角线互
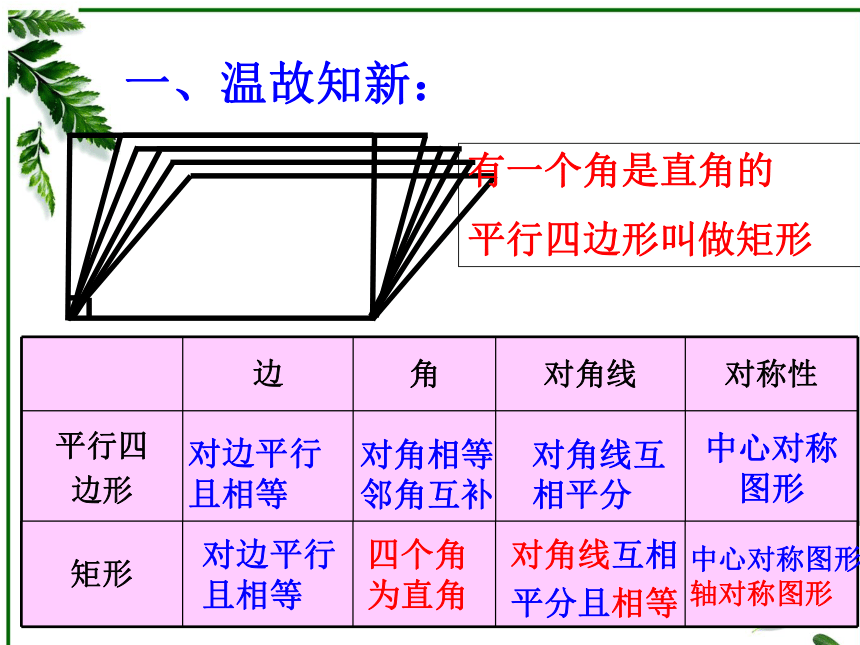
相平分中心对称图形一、温故知新:有一个角是直角的
平行四边形叫做矩形对边平行
且相等对角相等
邻角互补对角线互
相平分对边平行
且相等四个角
为直角对角线互相
平分且相等中心对称图形
轴对称图形一、温故知新:二、洋葱回放:
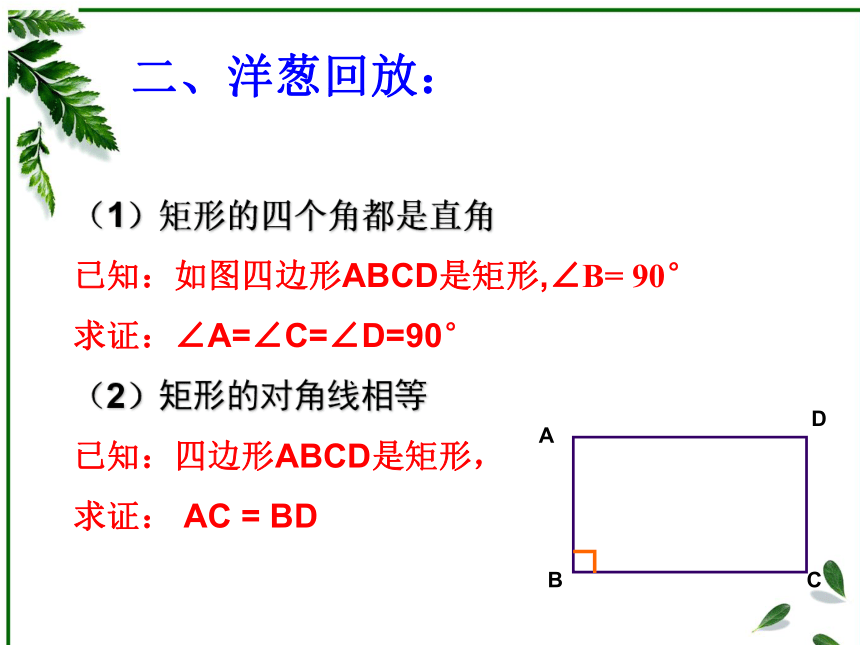
(1)矩形的四个角都是直角
已知:如图四边形ABCD是矩形,∠B= 90°
求证:∠A=∠C=∠D=90°
(2)矩形的对角线相等
已知:四边形ABCD是矩形,
求证: AC = BD
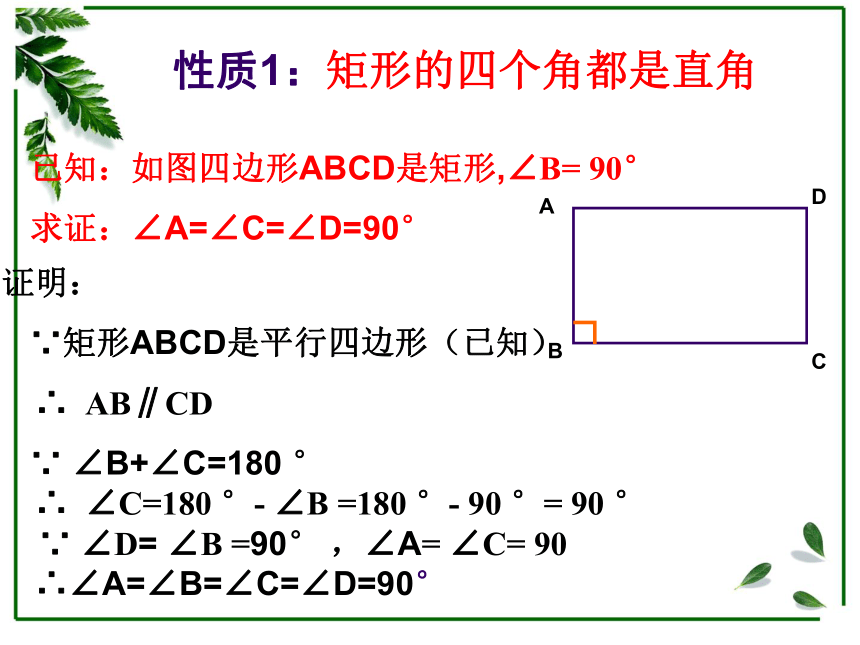
CBAD 性质1:矩形的四个角都是直角已知:如图四边形ABCD是矩形,∠B= 90°
求证:∠A=∠C=∠D=90°DCBA证明:
∵矩形ABCD是平行四边形(已知)
∴ AB∥CD
∵ ∠B+∠C=180 °
∴ ∠C=180 °- ∠B =180 °- 90 °= 90 °
∵ ∠D= ∠B =90° ,∠A= ∠C= 90
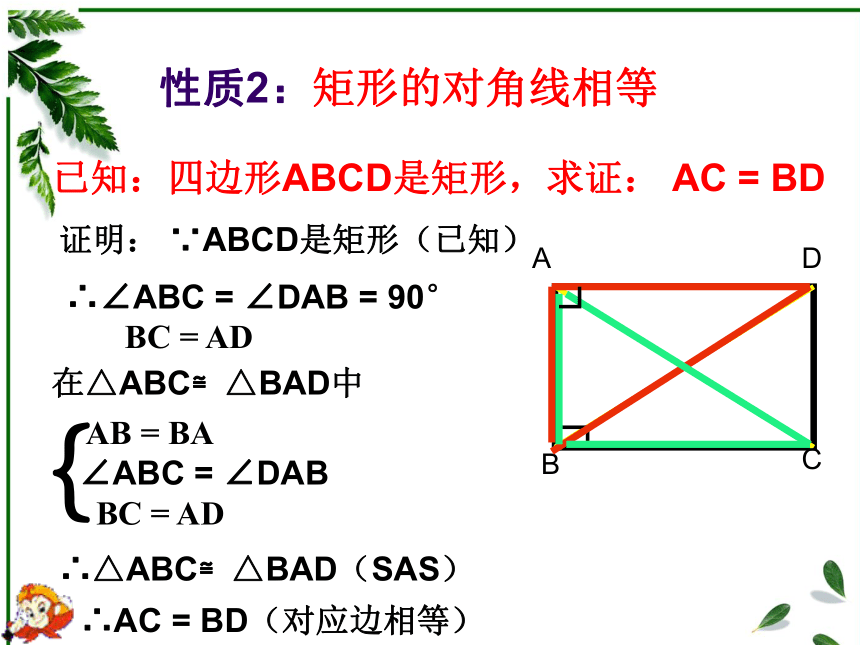
∴∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形,求证: AC = BD 证明: ∵ABCD是矩形(已知)∴∠ABC = ∠DAB = 90°
BC = AD∴△ABC≌△BAD(SAS)∴AC = BD(对应边相等)性质2:矩形的对角线相等在△ABC≌△BAD中 AB = BA
∠ABC = ∠DAB
BC = AD{观察后思考:1、如图,有几个直角三角形?分别是什么?请证明.
2、有几个等腰三角形?分别是什么?请证明.o3、请你添加一个条件,使△ABO是等边三角形.三、初步探究:例: 如图,矩形ABCD的两条对角线相交于点O, AB=4,矩形对角线的长?∠AOB=60°, AD = cm ,Do四、例题展示: 三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处.三个人的位置对每个人公平吗?请说明理由.五、深入探究:ODCBA┛在Rt△ABD中,AO是斜边BD的中线直角三角形斜边上中线的性质 :
直角三角形斜边上的中线等于斜边的一半。则有:AO= BD 在矩形ABCD中
AO=CO=BO=DO= AC= BD2、如图所示,BD⊥AC于D,CE⊥AB于E,M、N分别是BC、DE的中点,
求证:MN⊥DE我收获,我成长,我快乐直角三角形性质
直角三角形斜边上的中线等于斜边的一半推论解题指导:矩形问题 直角三角形或等腰三角形连接对角线
转化2、已知:如图所示,在矩形
ABCD中,AB=3,AD=4,
P是AD上的动点,PE⊥AC于
点E,PF⊥BD于点F,
则PE+PF=_________.
??1、如图:矩形ABCD中,对角线
AC、BD相交于点O,AE平分
∠BAD,连结OE,若∠CAE=15°
则∠BOE=________.
?六、洋葱反馈:课堂作业:课本第53页第2题
2.探索并证明矩形的性质,会用矩形的性质解决相关问题
3.理解“直角三角形斜边上的中线等于斜边 的一半”这一重要结论对边平行
且相等对角相等
邻角互补对角线互
相平分中心对称图形一、温故知新:有一个角是直角的
平行四边形叫做矩形对边平行
且相等对角相等
邻角互补对角线互
相平分对边平行
且相等四个角
为直角对角线互相
平分且相等中心对称图形
轴对称图形一、温故知新:二、洋葱回放:
(1)矩形的四个角都是直角
已知:如图四边形ABCD是矩形,∠B= 90°
求证:∠A=∠C=∠D=90°
(2)矩形的对角线相等
已知:四边形ABCD是矩形,
求证: AC = BD
CBAD 性质1:矩形的四个角都是直角已知:如图四边形ABCD是矩形,∠B= 90°
求证:∠A=∠C=∠D=90°DCBA证明:
∵矩形ABCD是平行四边形(已知)
∴ AB∥CD
∵ ∠B+∠C=180 °
∴ ∠C=180 °- ∠B =180 °- 90 °= 90 °
∵ ∠D= ∠B =90° ,∠A= ∠C= 90
∴∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形,求证: AC = BD 证明: ∵ABCD是矩形(已知)∴∠ABC = ∠DAB = 90°
BC = AD∴△ABC≌△BAD(SAS)∴AC = BD(对应边相等)性质2:矩形的对角线相等在△ABC≌△BAD中 AB = BA
∠ABC = ∠DAB
BC = AD{观察后思考:1、如图,有几个直角三角形?分别是什么?请证明.
2、有几个等腰三角形?分别是什么?请证明.o3、请你添加一个条件,使△ABO是等边三角形.三、初步探究:例: 如图,矩形ABCD的两条对角线相交于点O, AB=4,矩形对角线的长?∠AOB=60°, AD = cm ,Do四、例题展示: 三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处.三个人的位置对每个人公平吗?请说明理由.五、深入探究:ODCBA┛在Rt△ABD中,AO是斜边BD的中线直角三角形斜边上中线的性质 :
直角三角形斜边上的中线等于斜边的一半。则有:AO= BD 在矩形ABCD中
AO=CO=BO=DO= AC= BD2、如图所示,BD⊥AC于D,CE⊥AB于E,M、N分别是BC、DE的中点,
求证:MN⊥DE我收获,我成长,我快乐直角三角形性质
直角三角形斜边上的中线等于斜边的一半推论解题指导:矩形问题 直角三角形或等腰三角形连接对角线
转化2、已知:如图所示,在矩形
ABCD中,AB=3,AD=4,
P是AD上的动点,PE⊥AC于
点E,PF⊥BD于点F,
则PE+PF=_________.
??1、如图:矩形ABCD中,对角线
AC、BD相交于点O,AE平分
∠BAD,连结OE,若∠CAE=15°
则∠BOE=________.
?六、洋葱反馈:课堂作业:课本第53页第2题
