鲁教版(五四学制)六年级数学下册 第五章 基本平面图形 单元测试题(含解析)
文档属性
| 名称 | 鲁教版(五四学制)六年级数学下册 第五章 基本平面图形 单元测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 370.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 14:09:21 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
鲁教版(五四学制)六年级数学下册 第五章 基本平面图形 单元测试题(2024)
一、选择题(共10题;共30分)
1.(3分)如图,在学校的劳动实践课程上,同学们体验插秧时发现:只要确定两个秧苗的位置,就能使同一行秩苗整齐的插在一条直线上,这样做的依据是( )
A.两点确定一条直线 B.垂线段最短
C.两点之间线段最短 D.同角的余角相等
2.(3分)生活中,我们可以用身体中的“尺子”来估计长度,其中一拃是张开的大拇指尖和中指尖之间的最大距离(如图所示). 以下估计正确的是( )
A.一支水笔的长度约1拃 B.课桌的高度约2拃
C.黑板的长度约3拃 D.试卷的宽度约6拃
3.(3分)植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,这样做蕴含的数学原理是( )
A.两点确定一条直线 B.两点之间,线段最短
C.过一点有无数条线段 D.线段有两个端点
4.(3分)若,则的余角是( )
A. B. C. D.
5.(3分)如图,能用、、三种方法表示同一个角的是( )
A. B.
C. D.
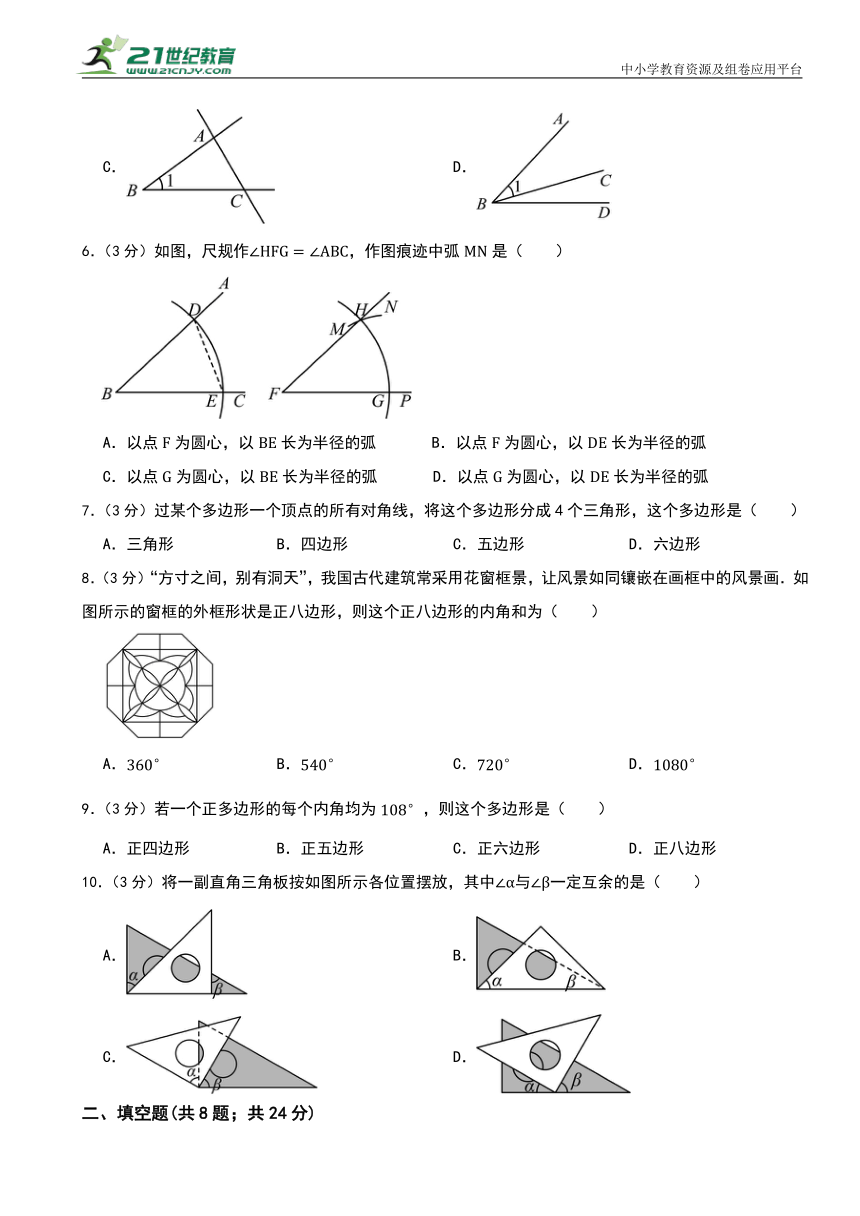
6.(3分)如图,尺规作,作图痕迹中弧是( )
A.以点为圆心,以长为半径的弧 B.以点为圆心,以长为半径的弧
C.以点为圆心,以长为半径的弧 D.以点为圆心,以长为半径的弧
7.(3分)过某个多边形一个顶点的所有对角线,将这个多边形分成4个三角形,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
8.(3分)“方寸之间,别有洞天”,我国古代建筑常采用花窗框景,让风景如同镶嵌在画框中的风景画.如图所示的窗框的外框形状是正八边形,则这个正八边形的内角和为( )
A. B. C. D.
9.(3分)若一个正多边形的每个内角均为,则这个多边形是( )
A.正四边形 B.正五边形 C.正六边形 D.正八边形
10.(3分)将一副直角三角板按如图所示各位置摆放,其中与一定互余的是( )
A. B.
C. D.
二、填空题(共8题;共24分)
11.(3分)在同一条直线上有三个点,,,则线段的长是 .
12.(3分)如图,在一张零件图纸中,,,,则的长为 .
13.(3分)如图,已知线段,点C是线段的中点,点D是线段的中点,E为线段上一点,若线段,则的长度为 .
14.(3分)如图点O在直线 BD上,已知∠COD=95°,AO⊥CO,则∠AOB 的度数为 。
15.(3分)若,则用度、分、秒表示为 .
16.(3分)从上午到当天上午,时钟的分针转过的角度为 °.
17.(3分)若一个多边形的内角和为,则这个多边形的边数是 .
18.(3分)如图,,则 度.
三、解答题(共8题;共66分)
19.(8分)如图,线段,点是线段的中点,点是线段的中点.求线段的长.
20.(8分)如图,线段,点是线段的中点.若点在线段上,且,求线段的长;
21.(8分)一个多边形的内角和为1260度,求它的边数.
22.(6分) 若一个多边形的内角和与外角和的比为,求这个多边形的边数.
23.(8分)如图,点C、D、E在线段AB上,且满足AC=CD=DB,点E是线段DB的中点,若线段CE=6cm,求线段AB的长.
24.(8分)如图,直线CD,AB 都过点O,∠BOD 和 互余, .
(1)(4分)求∠MOB 的度数.
(2)(4分)若 求∠BOD 的度数.
25.(8分)小军求一个多边形的内角和时,少加了一个内角,得到
(1)(4分)求少加的这个内角的度数.
(2)(4分)通过计算,判断这个多边形能否是正多边形.
26.(12分)如图 1 为某款家用可伸缩晾衣杆,晾衣杆由三部分组成,分别是长度固定的 和 两段以及可伸缩的 段, 最短可缩到比 短 ,最长可伸长到比 短 , .
(1)(6分)求该款晾衣杆可达到的最大长度和最短长度.
(2)(6分)如图 2,在 段伸缩的过程中,是否存在 “ ” 的情况?如果存在, 请求出此时 的长; 如果不存在,请说明理由.
答案解析部分
1.【答案】A
【知识点】两点确定一条直线
【解析】【解答】解:由题意可得:
只要确定两个秧苗的位置,就能使同一行秩苗整齐的插在一条直线上,这样做的依据是两点确定一条直线
故答案为:A
【分析】根据两点确定一条直线即可求出答案.
2.【答案】A
【知识点】直线、射线、线段
【解析】【解答】解:A.一支水笔的长度约1拃,估计正确,符合题意;
B. 课桌的高度约2拃,估计错误,不符合题意;
C. 黑板的长度约3拃,估计错误,不符合题意;
D. 试卷的宽度约6拃,估计错误,不符合题意;
故答案为:A.
【分析】联系生活实际判断即可解题.
3.【答案】A
【知识点】两点确定一条直线
【解析】【解答】解:将两个树坑看作两个点,所以植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,这样做蕴含的数学原理是两点确定一条直线.
故答案为:A.
【分析】根据两点确定一条直线即可求出答案.
4.【答案】D
【知识点】常用角的度量单位及换算
【解析】【解答】解:,则的余角是,
故选:D.
【分析】本题考查了求一个角的余角,如果两个角的和等于,则这两个角互为余角,即其中每一个角是另一个角的余角,据此求解,即可得到答案.
5.【答案】C
【知识点】角的概念及表示
【解析】【解答】解:中,由、、表示的不一定是同一个角,错误,∵以为顶点的有多个角,故A不符合题意;
中,由、、表示的不一定是同一个角,错误,∵以为顶点的有多个角,
故B不符合题意;
中,由、、表示的是同一个角,正确,故C符合题意;
中,由、、表示的不一定是同一个角,错误,∵以为顶点的有多个角,
故D不符合题意;
故选:C.
【分析】本题主要考查了角的表示方法, 把由两条有公共端点的射线组成的几何对象。角的两条射线叫做角的边,它们的公共端点叫做角的顶点 ,结合图形,逐项分析判断,即可求解.
6.【答案】D
【知识点】尺规作图-作一个角等于已知角
【解析】【解答】解:由图可知,(1)作射线,以点为圆心,以长为半径作弧,交射线于点;
(2)以点为圆心,以长为半径的作弧,交弧于点;
故弧是以点为圆心,以长为半径的弧;
故选:D
【分析】本题考查用尺规作相等的角, 在给定角的一边上选取一点作为圆心,画出一个圆;然后,利用圆的半径和给定点在给定角上的位置,找到另一个点作为新的圆心,再画出一个圆;最后,利用这两个圆的交点来构造与给定角相等的角,据此尺规作图,即可求解.
7.【答案】D
【知识点】多边形的对角线
【解析】【解答】解:根据多边形的性质,
∵,∴这个多边形是六边形.
故选:D.
【分析】本题考查了多边形的对角线,根据n边形从一个顶点出发,得到条对角线和个三角形,据此求解,即可得到但.
8.【答案】D
【知识点】多边形内角与外角
【解析】【解答】解:;
故答案为:D.
【分析】根据多边形的内角和公式即可求出答案.
9.【答案】B
【知识点】多边形内角与外角
【解析】【解答】解:一个正多边形的每个内角均为,
,
,
这个多边形是正五边形,
故答案为:B.
【分析】先求出正多边形的一个外角,再利用“正多边形的边数=外角和(360°)÷一个外角的度数”列出算式求解即可.
10.【答案】D
【知识点】角的运算
【解析】【解答】解:A、与不互余,选项不符合题意;
B、与不互余,选项不符合题意;
C、与相等但不一定互余,选项不符合题意;
D、因为,
所以与互余,选项符合题意;
故答案为:D.
【分析】依据余角的定义,以及各图中三角形的摆放方式判断解题.
11.【答案】3或9
【知识点】线段的和、差、倍、分的简单计算
【解析】【解答】解:当点在线段上,,
当点在的延长线上,,
综上所述,或,
故答案为:3或9.
【分析】本题考查两点间的距离,根据题意,分两点在线段上和点在线段的延长线上,两种情况讨论,结合线段的和差关系,列出算式,进行计算,即可得到答案.
12.【答案】
【知识点】线段的和、差、倍、分的简单计算
【解析】【解答】解:∵,,,
∴由线段的和差,得:
.
故答案为:
【分析】本题主要考查线段的和差的运算,根据题意和线段的和差关系,结合,进行计算,即可得到答案.
13.【答案】7
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:∵线段,点C是线段的中点
∴,
∵点D是线段的中点,
∴,
∴,
故答案为:7.
【分析】本题考查线段和差,以及中点求线段长,由点C是线段的中点,点D是线段的中点,求得,,结合,进行计算,即可求解.
14.【答案】5°
【知识点】角的运算
【解析】【解答】解:
故答案为:
【分析】先利用平角定义求出. 的度数,然后再根据垂直定义可得 从而利用角的和差关系,进行计算即可解答.
15.【答案】
【知识点】常用角的度量单位及换算
【解析】【解答】解:由,
则,
故答案为:.
【分析】本题主要考查了度分秒的换算,根据度分秒的换算方法,结合 利用1°等于60'(60分),1'等于60″(60秒)的关系,进行计算,即可得到答案.
16.【答案】
【知识点】钟面角
【解析】【解答】解:从上午到当天上午,
时钟一共走了分钟,
,
时钟的分针一分钟走,
.
故答案为:.
【分析】本题考查了时钟分钟转过的角度问题,先求得时钟的分针一分钟走,结合时钟一共走了分钟,然后乘以,进行计算求解,即可得到答案.
17.【答案】10
【知识点】多边形内角与外角
【解析】【解答】解:这个多边形的边数为,
由题意得,,
解得,
∴这个多边形的边数是,
故答案为:.
【分析】根据多边形的内角和公式计算即可求出答案.
18.【答案】40
【知识点】多边形内角与外角
【解析】【解答】解:,,
,
故答案为:.
【分析】根据多边形的外角和等于即可求出∠1的度数.
19.【答案】解:∵是线段的中点,,
∴,
∵是线段的中点,
∴,
∴.
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【分析】先根据条件“ 点是线段的中点,点是线段的中点 ”,分别求出,,再利用线段的和差,即可求出AD的长。
20.【答案】解:如图,点在线段上,且,
∵,点是线段的中点,
∴,
∵点在线段上,且,
∴.
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【分析】本题考查了线段的中点的性质,以及线段的和差计算,由点在线段上,且,根据点是线段的中点,得到,结合,列出算式,即可求解.
21.【答案】解:设这个多边形的边数为,
依题意,,
∴,
∴这个多边形的边数为.
【知识点】多边形内角与外角
【解析】【分析】本题考查多边形内角和公式.根据多边形的内角和公式:边形的内角和为,可列出方程,解方程可求出n的值,据此可求出答案.
22.【答案】解:设这个多边形的边数为,
则,解得.
即这个多边形的边数为9
【知识点】多边形内角与外角
【解析】【分析】 设这个多边形的边数为, 则多边形的内角和为(n-2)×180°,外角和等于360°,根据“ 多边形的内角和与外角和的比为 ”列出方程并解之即可.
23.【答案】解:由点C、D、E在线段AB上,且满足AC=CD=DB,得AC=CD=DB=AB.
由点E是线段DB的中点,得DE=DB=AB.
由线段的和差,得CE=CD+DE=6,
即AB+AB=6,
解得:AB=12.
线段AB的长是12cm
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【分析】根据线段中点的定义得到 DE=DB ,然后利用线段的和差得到关于AB的方程,解题即可.
24.【答案】(1)解:∵∠BOD 和∠AON 互余,
∴∠BOD+∠AON=90°,
∵∠AON=∠COM,
∵∠BOD+∠COM=90°,
∴
(2)解:设∠COM=x,则∠BOC=5x,
∴∠BOM=4x,
∵∠BOM=90°,
∴4x=90°,
解得x=22.5°,
即∠COM=22.5°,
∴
【知识点】角的运算
【解析】【分析】(1)根据余角的定义可得∠BOD+∠AON=90°,再根据平角的定义可求解;
(2)设∠COM=x,则∠BOC=5x,得∠BOM=4x,由∠BOM=90°可求得x=22.5°,进而可得 ∠BOD 的度数.
25.【答案】(1)解:设这个多边形的边数为n,
根据题意可得:,
解得:,
∵n为正整数,
∴,
∴,
∴少加的这个内角的度数为:;
(2)解:若这个多边形是正多边形,则每个外角的度数为:,
∴它的边数应等于,
由(1)可知,这个多边形的边数为,
∴这个多边形不是正多边形.
【知识点】多边形内角与外角
【解析】【分析】(1)设这个多边形的边数为n,再利用多边形的内角和可得,求出n的取值范围,可得n=14,最后求解即可;
(2)先求出正多边形的一个外角,再利用“正多边形的边数=外角和(360°)÷一个外角的度数”列出算式求解即可.
(1)解:设这个多边形的边数为n,则:,
解得:,
∵n为正整数,
∴,
∴,
∴少加的这个内角的度数为:;
(2)解:若这个多边形是正多边形,则每个外角的度数为:,
∴它的边数应等于,
由(1)可知,这个多边形的边数为,
∴这个多边形不是正多边形.
26.【答案】(1)解: ,,
∵最长为,最短为,
最大长度;
最短长度;
(2)解:,
,此时 ,符合题意.
当 伸缩到 时满足条件
【知识点】线段的和、差、倍、分的简单计算
【解析】【分析】(1)先得到,然后根据最长为,最短为,解题即可;
(2)根据得到,然后解题即可.
(1)解: ,
,
∵最长为,最短为,
最大长度;
最短长度;
(2)解:,
,此时 ,符合题意.
当 伸缩到 时满足条件.
鲁教版(五四学制)六年级数学下册 第五章 基本平面图形 单元测试题(2024)
一、选择题(共10题;共30分)
1.(3分)如图,在学校的劳动实践课程上,同学们体验插秧时发现:只要确定两个秧苗的位置,就能使同一行秩苗整齐的插在一条直线上,这样做的依据是( )
A.两点确定一条直线 B.垂线段最短
C.两点之间线段最短 D.同角的余角相等
2.(3分)生活中,我们可以用身体中的“尺子”来估计长度,其中一拃是张开的大拇指尖和中指尖之间的最大距离(如图所示). 以下估计正确的是( )
A.一支水笔的长度约1拃 B.课桌的高度约2拃
C.黑板的长度约3拃 D.试卷的宽度约6拃
3.(3分)植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,这样做蕴含的数学原理是( )
A.两点确定一条直线 B.两点之间,线段最短
C.过一点有无数条线段 D.线段有两个端点
4.(3分)若,则的余角是( )
A. B. C. D.
5.(3分)如图,能用、、三种方法表示同一个角的是( )
A. B.
C. D.
6.(3分)如图,尺规作,作图痕迹中弧是( )
A.以点为圆心,以长为半径的弧 B.以点为圆心,以长为半径的弧
C.以点为圆心,以长为半径的弧 D.以点为圆心,以长为半径的弧
7.(3分)过某个多边形一个顶点的所有对角线,将这个多边形分成4个三角形,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
8.(3分)“方寸之间,别有洞天”,我国古代建筑常采用花窗框景,让风景如同镶嵌在画框中的风景画.如图所示的窗框的外框形状是正八边形,则这个正八边形的内角和为( )
A. B. C. D.
9.(3分)若一个正多边形的每个内角均为,则这个多边形是( )
A.正四边形 B.正五边形 C.正六边形 D.正八边形
10.(3分)将一副直角三角板按如图所示各位置摆放,其中与一定互余的是( )
A. B.
C. D.
二、填空题(共8题;共24分)
11.(3分)在同一条直线上有三个点,,,则线段的长是 .
12.(3分)如图,在一张零件图纸中,,,,则的长为 .
13.(3分)如图,已知线段,点C是线段的中点,点D是线段的中点,E为线段上一点,若线段,则的长度为 .
14.(3分)如图点O在直线 BD上,已知∠COD=95°,AO⊥CO,则∠AOB 的度数为 。
15.(3分)若,则用度、分、秒表示为 .
16.(3分)从上午到当天上午,时钟的分针转过的角度为 °.
17.(3分)若一个多边形的内角和为,则这个多边形的边数是 .
18.(3分)如图,,则 度.
三、解答题(共8题;共66分)
19.(8分)如图,线段,点是线段的中点,点是线段的中点.求线段的长.
20.(8分)如图,线段,点是线段的中点.若点在线段上,且,求线段的长;
21.(8分)一个多边形的内角和为1260度,求它的边数.
22.(6分) 若一个多边形的内角和与外角和的比为,求这个多边形的边数.
23.(8分)如图,点C、D、E在线段AB上,且满足AC=CD=DB,点E是线段DB的中点,若线段CE=6cm,求线段AB的长.
24.(8分)如图,直线CD,AB 都过点O,∠BOD 和 互余, .
(1)(4分)求∠MOB 的度数.
(2)(4分)若 求∠BOD 的度数.
25.(8分)小军求一个多边形的内角和时,少加了一个内角,得到
(1)(4分)求少加的这个内角的度数.
(2)(4分)通过计算,判断这个多边形能否是正多边形.
26.(12分)如图 1 为某款家用可伸缩晾衣杆,晾衣杆由三部分组成,分别是长度固定的 和 两段以及可伸缩的 段, 最短可缩到比 短 ,最长可伸长到比 短 , .
(1)(6分)求该款晾衣杆可达到的最大长度和最短长度.
(2)(6分)如图 2,在 段伸缩的过程中,是否存在 “ ” 的情况?如果存在, 请求出此时 的长; 如果不存在,请说明理由.
答案解析部分
1.【答案】A
【知识点】两点确定一条直线
【解析】【解答】解:由题意可得:
只要确定两个秧苗的位置,就能使同一行秩苗整齐的插在一条直线上,这样做的依据是两点确定一条直线
故答案为:A
【分析】根据两点确定一条直线即可求出答案.
2.【答案】A
【知识点】直线、射线、线段
【解析】【解答】解:A.一支水笔的长度约1拃,估计正确,符合题意;
B. 课桌的高度约2拃,估计错误,不符合题意;
C. 黑板的长度约3拃,估计错误,不符合题意;
D. 试卷的宽度约6拃,估计错误,不符合题意;
故答案为:A.
【分析】联系生活实际判断即可解题.
3.【答案】A
【知识点】两点确定一条直线
【解析】【解答】解:将两个树坑看作两个点,所以植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,这样做蕴含的数学原理是两点确定一条直线.
故答案为:A.
【分析】根据两点确定一条直线即可求出答案.
4.【答案】D
【知识点】常用角的度量单位及换算
【解析】【解答】解:,则的余角是,
故选:D.
【分析】本题考查了求一个角的余角,如果两个角的和等于,则这两个角互为余角,即其中每一个角是另一个角的余角,据此求解,即可得到答案.
5.【答案】C
【知识点】角的概念及表示
【解析】【解答】解:中,由、、表示的不一定是同一个角,错误,∵以为顶点的有多个角,故A不符合题意;
中,由、、表示的不一定是同一个角,错误,∵以为顶点的有多个角,
故B不符合题意;
中,由、、表示的是同一个角,正确,故C符合题意;
中,由、、表示的不一定是同一个角,错误,∵以为顶点的有多个角,
故D不符合题意;
故选:C.
【分析】本题主要考查了角的表示方法, 把由两条有公共端点的射线组成的几何对象。角的两条射线叫做角的边,它们的公共端点叫做角的顶点 ,结合图形,逐项分析判断,即可求解.
6.【答案】D
【知识点】尺规作图-作一个角等于已知角
【解析】【解答】解:由图可知,(1)作射线,以点为圆心,以长为半径作弧,交射线于点;
(2)以点为圆心,以长为半径的作弧,交弧于点;
故弧是以点为圆心,以长为半径的弧;
故选:D
【分析】本题考查用尺规作相等的角, 在给定角的一边上选取一点作为圆心,画出一个圆;然后,利用圆的半径和给定点在给定角上的位置,找到另一个点作为新的圆心,再画出一个圆;最后,利用这两个圆的交点来构造与给定角相等的角,据此尺规作图,即可求解.
7.【答案】D
【知识点】多边形的对角线
【解析】【解答】解:根据多边形的性质,
∵,∴这个多边形是六边形.
故选:D.
【分析】本题考查了多边形的对角线,根据n边形从一个顶点出发,得到条对角线和个三角形,据此求解,即可得到但.
8.【答案】D
【知识点】多边形内角与外角
【解析】【解答】解:;
故答案为:D.
【分析】根据多边形的内角和公式即可求出答案.
9.【答案】B
【知识点】多边形内角与外角
【解析】【解答】解:一个正多边形的每个内角均为,
,
,
这个多边形是正五边形,
故答案为:B.
【分析】先求出正多边形的一个外角,再利用“正多边形的边数=外角和(360°)÷一个外角的度数”列出算式求解即可.
10.【答案】D
【知识点】角的运算
【解析】【解答】解:A、与不互余,选项不符合题意;
B、与不互余,选项不符合题意;
C、与相等但不一定互余,选项不符合题意;
D、因为,
所以与互余,选项符合题意;
故答案为:D.
【分析】依据余角的定义,以及各图中三角形的摆放方式判断解题.
11.【答案】3或9
【知识点】线段的和、差、倍、分的简单计算
【解析】【解答】解:当点在线段上,,
当点在的延长线上,,
综上所述,或,
故答案为:3或9.
【分析】本题考查两点间的距离,根据题意,分两点在线段上和点在线段的延长线上,两种情况讨论,结合线段的和差关系,列出算式,进行计算,即可得到答案.
12.【答案】
【知识点】线段的和、差、倍、分的简单计算
【解析】【解答】解:∵,,,
∴由线段的和差,得:
.
故答案为:
【分析】本题主要考查线段的和差的运算,根据题意和线段的和差关系,结合,进行计算,即可得到答案.
13.【答案】7
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【解答】解:∵线段,点C是线段的中点
∴,
∵点D是线段的中点,
∴,
∴,
故答案为:7.
【分析】本题考查线段和差,以及中点求线段长,由点C是线段的中点,点D是线段的中点,求得,,结合,进行计算,即可求解.
14.【答案】5°
【知识点】角的运算
【解析】【解答】解:
故答案为:
【分析】先利用平角定义求出. 的度数,然后再根据垂直定义可得 从而利用角的和差关系,进行计算即可解答.
15.【答案】
【知识点】常用角的度量单位及换算
【解析】【解答】解:由,
则,
故答案为:.
【分析】本题主要考查了度分秒的换算,根据度分秒的换算方法,结合 利用1°等于60'(60分),1'等于60″(60秒)的关系,进行计算,即可得到答案.
16.【答案】
【知识点】钟面角
【解析】【解答】解:从上午到当天上午,
时钟一共走了分钟,
,
时钟的分针一分钟走,
.
故答案为:.
【分析】本题考查了时钟分钟转过的角度问题,先求得时钟的分针一分钟走,结合时钟一共走了分钟,然后乘以,进行计算求解,即可得到答案.
17.【答案】10
【知识点】多边形内角与外角
【解析】【解答】解:这个多边形的边数为,
由题意得,,
解得,
∴这个多边形的边数是,
故答案为:.
【分析】根据多边形的内角和公式计算即可求出答案.
18.【答案】40
【知识点】多边形内角与外角
【解析】【解答】解:,,
,
故答案为:.
【分析】根据多边形的外角和等于即可求出∠1的度数.
19.【答案】解:∵是线段的中点,,
∴,
∵是线段的中点,
∴,
∴.
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【分析】先根据条件“ 点是线段的中点,点是线段的中点 ”,分别求出,,再利用线段的和差,即可求出AD的长。
20.【答案】解:如图,点在线段上,且,
∵,点是线段的中点,
∴,
∵点在线段上,且,
∴.
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【分析】本题考查了线段的中点的性质,以及线段的和差计算,由点在线段上,且,根据点是线段的中点,得到,结合,列出算式,即可求解.
21.【答案】解:设这个多边形的边数为,
依题意,,
∴,
∴这个多边形的边数为.
【知识点】多边形内角与外角
【解析】【分析】本题考查多边形内角和公式.根据多边形的内角和公式:边形的内角和为,可列出方程,解方程可求出n的值,据此可求出答案.
22.【答案】解:设这个多边形的边数为,
则,解得.
即这个多边形的边数为9
【知识点】多边形内角与外角
【解析】【分析】 设这个多边形的边数为, 则多边形的内角和为(n-2)×180°,外角和等于360°,根据“ 多边形的内角和与外角和的比为 ”列出方程并解之即可.
23.【答案】解:由点C、D、E在线段AB上,且满足AC=CD=DB,得AC=CD=DB=AB.
由点E是线段DB的中点,得DE=DB=AB.
由线段的和差,得CE=CD+DE=6,
即AB+AB=6,
解得:AB=12.
线段AB的长是12cm
【知识点】线段的中点;线段的和、差、倍、分的简单计算
【解析】【分析】根据线段中点的定义得到 DE=DB ,然后利用线段的和差得到关于AB的方程,解题即可.
24.【答案】(1)解:∵∠BOD 和∠AON 互余,
∴∠BOD+∠AON=90°,
∵∠AON=∠COM,
∵∠BOD+∠COM=90°,
∴
(2)解:设∠COM=x,则∠BOC=5x,
∴∠BOM=4x,
∵∠BOM=90°,
∴4x=90°,
解得x=22.5°,
即∠COM=22.5°,
∴
【知识点】角的运算
【解析】【分析】(1)根据余角的定义可得∠BOD+∠AON=90°,再根据平角的定义可求解;
(2)设∠COM=x,则∠BOC=5x,得∠BOM=4x,由∠BOM=90°可求得x=22.5°,进而可得 ∠BOD 的度数.
25.【答案】(1)解:设这个多边形的边数为n,
根据题意可得:,
解得:,
∵n为正整数,
∴,
∴,
∴少加的这个内角的度数为:;
(2)解:若这个多边形是正多边形,则每个外角的度数为:,
∴它的边数应等于,
由(1)可知,这个多边形的边数为,
∴这个多边形不是正多边形.
【知识点】多边形内角与外角
【解析】【分析】(1)设这个多边形的边数为n,再利用多边形的内角和可得,求出n的取值范围,可得n=14,最后求解即可;
(2)先求出正多边形的一个外角,再利用“正多边形的边数=外角和(360°)÷一个外角的度数”列出算式求解即可.
(1)解:设这个多边形的边数为n,则:,
解得:,
∵n为正整数,
∴,
∴,
∴少加的这个内角的度数为:;
(2)解:若这个多边形是正多边形,则每个外角的度数为:,
∴它的边数应等于,
由(1)可知,这个多边形的边数为,
∴这个多边形不是正多边形.
26.【答案】(1)解: ,,
∵最长为,最短为,
最大长度;
最短长度;
(2)解:,
,此时 ,符合题意.
当 伸缩到 时满足条件
【知识点】线段的和、差、倍、分的简单计算
【解析】【分析】(1)先得到,然后根据最长为,最短为,解题即可;
(2)根据得到,然后解题即可.
(1)解: ,
,
∵最长为,最短为,
最大长度;
最短长度;
(2)解:,
,此时 ,符合题意.
当 伸缩到 时满足条件.
同课章节目录
