苏教版高中数学必修第二册-9.1向量概念-同步练习(含解析)
文档属性
| 名称 | 苏教版高中数学必修第二册-9.1向量概念-同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 456.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-07 11:02:47 | ||
图片预览


文档简介
高中数学同步资源QQ群483122854 专注收集成套同步资源,成套的教案,成套的课件,成套的试题,成套的微专题 期待你的加入与分享
苏教版高中数学必修第二册-9.1向量概念-同步练习
必备知识基础练
1.下列结论中正确的有( )
A.温度含零上和零下温度,所以温度是向量
B.共线的向量,若始点不同,则终点一定不同
C.向量a与b不共线,则a与b都是非零向量
D.若|a|>|b|,则a>b
2.如图所示,梯形ABCD为等腰梯形,则两腰上的向量的关系是( )
A. B.||=||
C. D.
3.设O是△ABC的外心,则是( )
A.相等向量 B.模相等的向量
C.平行向量 D.起点相同的向量
4.在四边形ABCD中,若且||=||,则该四边形的形状为 .
5.有下列说法:
①若a≠b,则a一定不与b共线;
②若,则A,B,C,D四点是平行四边形的四个顶点;
③在 ABCD中,一定有;
④共线向量是在一条直线上的向量.
其中,正确的说法有 .(填序号)
6.如图所示,E,F分别为△ABC的边AB,AC的中点,则与向量共线的向量有 .(写出图中所有符合条件的向量)
7.
如图,D,E,F分别是正三角形ABC各边的中点.
(1)写出图中所示向量中与向量长度相等的向量;
(2)分别写出图中所示向量中与向量共线的向量;
(3)求的夹角的度数.
关键能力提升练
8.下列说法正确的是( )
A.共线的两个单位向量方向相同或相反
B.相等向量的起点相同
C.若,则一定有直线AB∥CD
D.若向量共线,则点A,B,C,D必在同一直线上
9.在如图所示的半圆中,AB为直径,点O为圆心,C为半圆上一点,且∠OCB=30°,||=2,则||等于( )
A.1 B.
C. D.2
10.如图所示,四边形ABCD,CEFG,CGHD是全等的菱形,则下列结论中不一定成立的是( )
A.||=||
B.共线
C.共线
D.
11.(多选)下列说法正确的是( )
A.若a=0,则|a|=0
B.零向量是没有方向的
C.零向量与任一向量平行
D.零向量的方向是任意的
12.(多选)设点O是正方形ABCD的中心,则下列结论正确的是( )
A. B.
C.共线 D.
13.(多选)已知A={与a共线的向量},B={与a长度相等的向量},C={与a长度相等方向相反的向量},其中a为非零向量,则下列说法正确的是 ( )
A.C A B.A∩B={a}
C.C B D.A∩B {a}
14.把同一平面内所有模不小于1,不大于2的向量的起点,移到同一点O,则这些向量的终点构成的图形的面积等于 .
15.给出下列四个条件:①a=b;②|a|=|b|;③a与b方向相反;④|a|=0或|b|=0.其中能使a∥b成立的条件是 .(填序号)
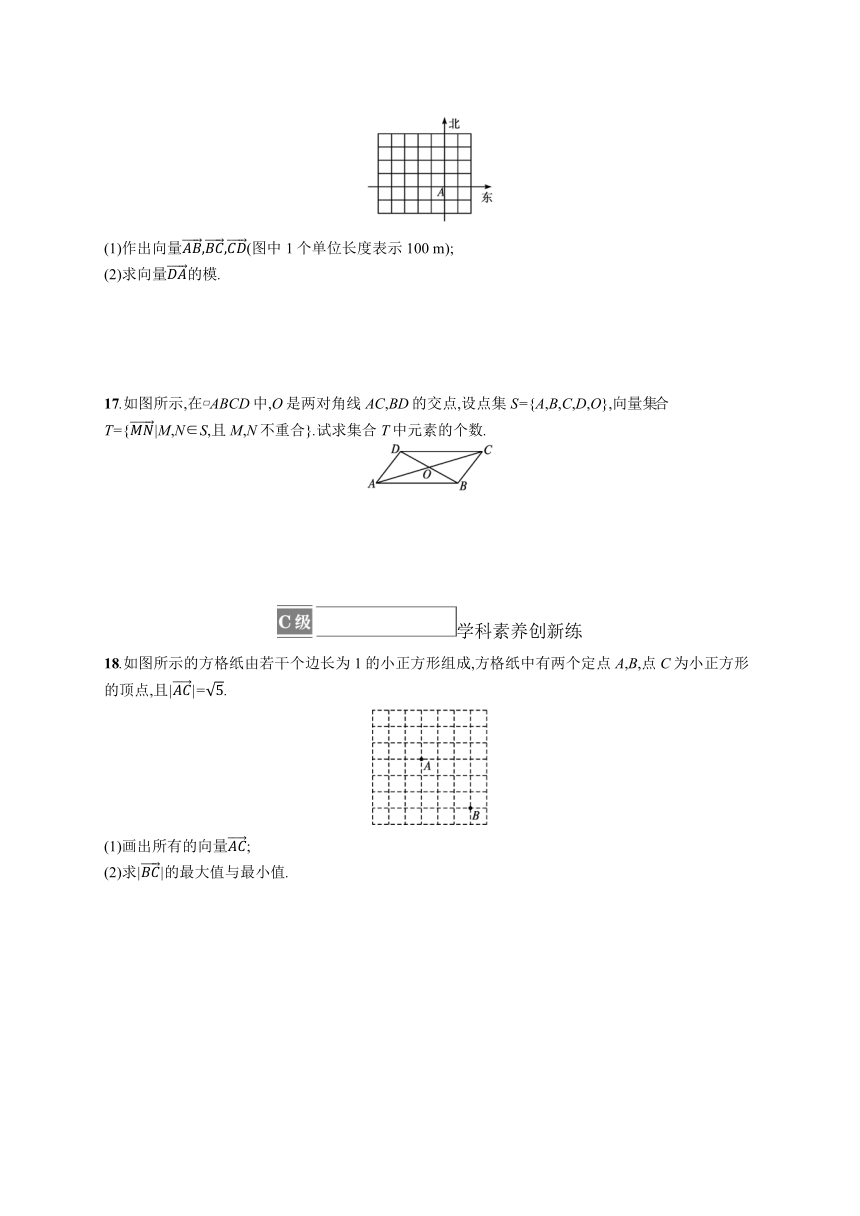
16.某人从点A出发,向西走了200 m后到达点B,然后改变方向,向北偏西一定角度的某方向行走了100 m到达点C,最后又改变方向,向东走了200 m到达点D,发现点D在点B的正北方.
(1)作出向量(图中1个单位长度表示100 m);
(2)求向量的模.
17.如图所示,在 ABCD中,O是两对角线AC,BD的交点,设点集S={A,B,C,D,O},向量集合T={|M,N∈S,且M,N不重合}.试求集合T中元素的个数.
学科素养创新练
18.如图所示的方格纸由若干个边长为1的小正方形组成,方格纸中有两个定点A,B,点C为小正方形的顶点,且||=.
(1)画出所有的向量;
(2)求||的最大值与最小值.
参考答案与详细解析
必备知识基础练
1.答案C
解析温度没有方向,所以不是向量,故A错;由共线向量的定义可知,共线的向量,始点不同,终点可能相同,故B错;向量不可以比较大小,故D错;C项中,若a,b中有一个为零向量,则a与b必共线,故若a与b不共线,则应均为非零向量,故C对.
2.答案B
3.答案B
解析因为O是△ABC的外心,所以||=||=||.
4.答案菱形
解析∵,∴AB=DC,AB∥DC,
∴四边形ABCD是平行四边形.
又||=||,∴四边形ABCD是菱形.
5.答案③
解析对于①,两个向量不相等,可能是长度不相等,但方向相同或相反,所以a与b有共线的可能,故①不正确;对于②,A,B,C,D四点可能在同一条直线上,故②不正确;对于③,在 ABCD中,||=||,平行且方向相同,所以,故③正确;对于④,共线向量可以是在一条直线上的向量,也可以是所在直线互相平行的向量,故④不正确.
6.答案
解析∵E,F分别为△ABC的边AB,AC的中点,
∴EF∥BC,∴符合条件的向量有.
7.解(1)与长度相等的向量是.
(2)与共线的向量是;
与共线的向量是.
(3)因为△ABC为正三角形,的夹角为∠ABC=60°,故的夹角为60°.的夹角为∠AFD的补角,故的夹角为120°.
关键能力提升练
8.答案A
解析A对,共线的两个单位向量的方向相同或相反;B错,相等向量的起点和终点都可能不相同;C错,直线AB与CD可能重合;D错,AB与CD可能平行,则A,B,C,D四点不一定在同一直线上.故选A.
9.答案A
解析如图,连接AC,由||=||,得∠ABC=∠OCB=30°,又∠ACB=90°,则||=|=×2=1.
10.答案C
11.答案ACD
12.答案ABC
解析如图,∵方向相同,长度相等,∴选项A正确;
∵的方向相反,∴,选项B正确;
∵AB∥CD,∴共线,∴选项C正确;
∵方向不同,∴,∴选项D错误.故选ABC.
13.答案ACD
解析与a共线的向量是与其方向相同或相反的向量,所以C A,故A对;因为A∩B={a,-a},故B错;B中的向量与a的长度相等,方向任意,故C B,故C对;A∩B={a,-a},所以A∩B {a},故D对.故选ACD.
14.解析依题意,这些向量的终点构成的图形是以点O为圆心,2为半径的圆,挖去一个以点O为圆心,1为半径的圆所围成的圆环,其面积为4π-π=3π.
15.答案①③④
解析若a=b,则a与b大小相等且方向相同,所以a∥b;若|a|=|b|,则a与b的大小相等,而方向不确定,因此不一定有a∥b;方向相同或相反的向量都是平行向量,因此若a与b方向相反,则a∥b;零向量与任意向量平行,所以若|a|=0或|b|=0,则a∥b.
16.解(1)如图.
(2)由题意可知,四边形ABCD是平行四边形,
所以||=||=100(m).
17.解由题意可知,由集合S中任意两点连成的有向线段共有20个,即.
由平行四边形的性质可知,共有8对相等向量,即.
因为集合中元素具有互异性,所以集合T中的元素共有20-8=12个.
学科素养创新练
18.解(1)
画出所有的向量如图所示.
(2)由(1)所画的图知,
①当点C位于点C1或C2时,||取得最小值;
②当点C位于点C5或C6时,||取得最大值.
所以||的最大值为,最小值为.
高中数学同步资源QQ群483122854 专注收集成套同步资源,成套的教案,成套的课件,成套的试题,成套的微专题 期待你的加入与分享
苏教版高中数学必修第二册-9.1向量概念-同步练习
必备知识基础练
1.下列结论中正确的有( )
A.温度含零上和零下温度,所以温度是向量
B.共线的向量,若始点不同,则终点一定不同
C.向量a与b不共线,则a与b都是非零向量
D.若|a|>|b|,则a>b
2.如图所示,梯形ABCD为等腰梯形,则两腰上的向量的关系是( )
A. B.||=||
C. D.
3.设O是△ABC的外心,则是( )
A.相等向量 B.模相等的向量
C.平行向量 D.起点相同的向量
4.在四边形ABCD中,若且||=||,则该四边形的形状为 .
5.有下列说法:
①若a≠b,则a一定不与b共线;
②若,则A,B,C,D四点是平行四边形的四个顶点;
③在 ABCD中,一定有;
④共线向量是在一条直线上的向量.
其中,正确的说法有 .(填序号)
6.如图所示,E,F分别为△ABC的边AB,AC的中点,则与向量共线的向量有 .(写出图中所有符合条件的向量)
7.
如图,D,E,F分别是正三角形ABC各边的中点.
(1)写出图中所示向量中与向量长度相等的向量;
(2)分别写出图中所示向量中与向量共线的向量;
(3)求的夹角的度数.
关键能力提升练
8.下列说法正确的是( )
A.共线的两个单位向量方向相同或相反
B.相等向量的起点相同
C.若,则一定有直线AB∥CD
D.若向量共线,则点A,B,C,D必在同一直线上
9.在如图所示的半圆中,AB为直径,点O为圆心,C为半圆上一点,且∠OCB=30°,||=2,则||等于( )
A.1 B.
C. D.2
10.如图所示,四边形ABCD,CEFG,CGHD是全等的菱形,则下列结论中不一定成立的是( )
A.||=||
B.共线
C.共线
D.
11.(多选)下列说法正确的是( )
A.若a=0,则|a|=0
B.零向量是没有方向的
C.零向量与任一向量平行
D.零向量的方向是任意的
12.(多选)设点O是正方形ABCD的中心,则下列结论正确的是( )
A. B.
C.共线 D.
13.(多选)已知A={与a共线的向量},B={与a长度相等的向量},C={与a长度相等方向相反的向量},其中a为非零向量,则下列说法正确的是 ( )
A.C A B.A∩B={a}
C.C B D.A∩B {a}
14.把同一平面内所有模不小于1,不大于2的向量的起点,移到同一点O,则这些向量的终点构成的图形的面积等于 .
15.给出下列四个条件:①a=b;②|a|=|b|;③a与b方向相反;④|a|=0或|b|=0.其中能使a∥b成立的条件是 .(填序号)
16.某人从点A出发,向西走了200 m后到达点B,然后改变方向,向北偏西一定角度的某方向行走了100 m到达点C,最后又改变方向,向东走了200 m到达点D,发现点D在点B的正北方.
(1)作出向量(图中1个单位长度表示100 m);
(2)求向量的模.
17.如图所示,在 ABCD中,O是两对角线AC,BD的交点,设点集S={A,B,C,D,O},向量集合T={|M,N∈S,且M,N不重合}.试求集合T中元素的个数.
学科素养创新练
18.如图所示的方格纸由若干个边长为1的小正方形组成,方格纸中有两个定点A,B,点C为小正方形的顶点,且||=.
(1)画出所有的向量;
(2)求||的最大值与最小值.
参考答案与详细解析
必备知识基础练
1.答案C
解析温度没有方向,所以不是向量,故A错;由共线向量的定义可知,共线的向量,始点不同,终点可能相同,故B错;向量不可以比较大小,故D错;C项中,若a,b中有一个为零向量,则a与b必共线,故若a与b不共线,则应均为非零向量,故C对.
2.答案B
3.答案B
解析因为O是△ABC的外心,所以||=||=||.
4.答案菱形
解析∵,∴AB=DC,AB∥DC,
∴四边形ABCD是平行四边形.
又||=||,∴四边形ABCD是菱形.
5.答案③
解析对于①,两个向量不相等,可能是长度不相等,但方向相同或相反,所以a与b有共线的可能,故①不正确;对于②,A,B,C,D四点可能在同一条直线上,故②不正确;对于③,在 ABCD中,||=||,平行且方向相同,所以,故③正确;对于④,共线向量可以是在一条直线上的向量,也可以是所在直线互相平行的向量,故④不正确.
6.答案
解析∵E,F分别为△ABC的边AB,AC的中点,
∴EF∥BC,∴符合条件的向量有.
7.解(1)与长度相等的向量是.
(2)与共线的向量是;
与共线的向量是.
(3)因为△ABC为正三角形,的夹角为∠ABC=60°,故的夹角为60°.的夹角为∠AFD的补角,故的夹角为120°.
关键能力提升练
8.答案A
解析A对,共线的两个单位向量的方向相同或相反;B错,相等向量的起点和终点都可能不相同;C错,直线AB与CD可能重合;D错,AB与CD可能平行,则A,B,C,D四点不一定在同一直线上.故选A.
9.答案A
解析如图,连接AC,由||=||,得∠ABC=∠OCB=30°,又∠ACB=90°,则||=|=×2=1.
10.答案C
11.答案ACD
12.答案ABC
解析如图,∵方向相同,长度相等,∴选项A正确;
∵的方向相反,∴,选项B正确;
∵AB∥CD,∴共线,∴选项C正确;
∵方向不同,∴,∴选项D错误.故选ABC.
13.答案ACD
解析与a共线的向量是与其方向相同或相反的向量,所以C A,故A对;因为A∩B={a,-a},故B错;B中的向量与a的长度相等,方向任意,故C B,故C对;A∩B={a,-a},所以A∩B {a},故D对.故选ACD.
14.解析依题意,这些向量的终点构成的图形是以点O为圆心,2为半径的圆,挖去一个以点O为圆心,1为半径的圆所围成的圆环,其面积为4π-π=3π.
15.答案①③④
解析若a=b,则a与b大小相等且方向相同,所以a∥b;若|a|=|b|,则a与b的大小相等,而方向不确定,因此不一定有a∥b;方向相同或相反的向量都是平行向量,因此若a与b方向相反,则a∥b;零向量与任意向量平行,所以若|a|=0或|b|=0,则a∥b.
16.解(1)如图.
(2)由题意可知,四边形ABCD是平行四边形,
所以||=||=100(m).
17.解由题意可知,由集合S中任意两点连成的有向线段共有20个,即.
由平行四边形的性质可知,共有8对相等向量,即.
因为集合中元素具有互异性,所以集合T中的元素共有20-8=12个.
学科素养创新练
18.解(1)
画出所有的向量如图所示.
(2)由(1)所画的图知,
①当点C位于点C1或C2时,||取得最小值;
②当点C位于点C5或C6时,||取得最大值.
所以||的最大值为,最小值为.
高中数学同步资源QQ群483122854 专注收集成套同步资源,成套的教案,成套的课件,成套的试题,成套的微专题 期待你的加入与分享
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
