7.4平行线的性质 培优练习(无答案) 2024—2025学年北师大版数学八年级上册
文档属性
| 名称 | 7.4平行线的性质 培优练习(无答案) 2024—2025学年北师大版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 440.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-07 00:00:00 | ||
图片预览


文档简介
7.4平行线的性质培优练习北师大版2024—2025学年八年级上册
夯实基础:
1、平行线的性质:
⑴ 两条直线平行,同位角 .
⑵ 两条直线平行,内错角 .
⑶ 两条直线平行, 同旁内角 .
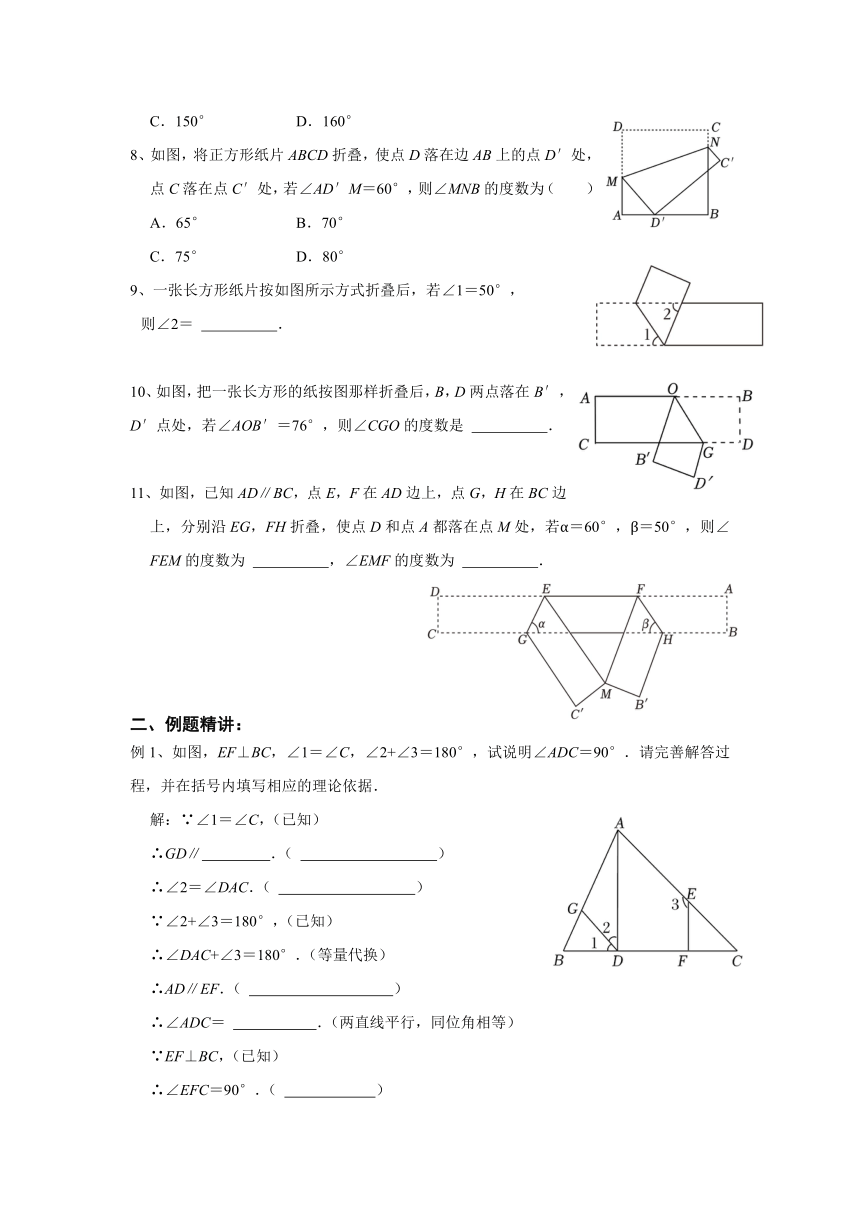
2、如图,将一张含有30°角的三角形纸片的两个顶点分别叠放在长方形的两条对边上.若∠2=40°,则∠1的度数为( )
A.10° B.20°
C.90°﹣α D.α﹣40°
3、已知直线m∥n,将一块直角三角板按如图所示方式放置,其中三角板的两个顶点分别落在直线m、n上,若∠1=55°,则∠2的度数是( )
A.25° B.30°
C.35° D.40°
4、如图,直线a∥b,∠1=65°,∠B=45°,则∠2的度数为( )
A.105° B.110°
C.117° D.125°
5、如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=48°,那么∠2的度数是( )
A.48° B.78°
C.92° D.102°
6、如图,直线a∥b,将直角三角板的直角顶点放在直线b上,已知∠1=55°,则∠2的度数为( )
A.35° B.45°
C.55° D.125°
7、如图是路政工程车的工作示意图,工作篮底部与支撑平台平行.若∠1=30°,∠2=50°,则∠3的度数为( )
A.130° B.140°
C.150° D.160°
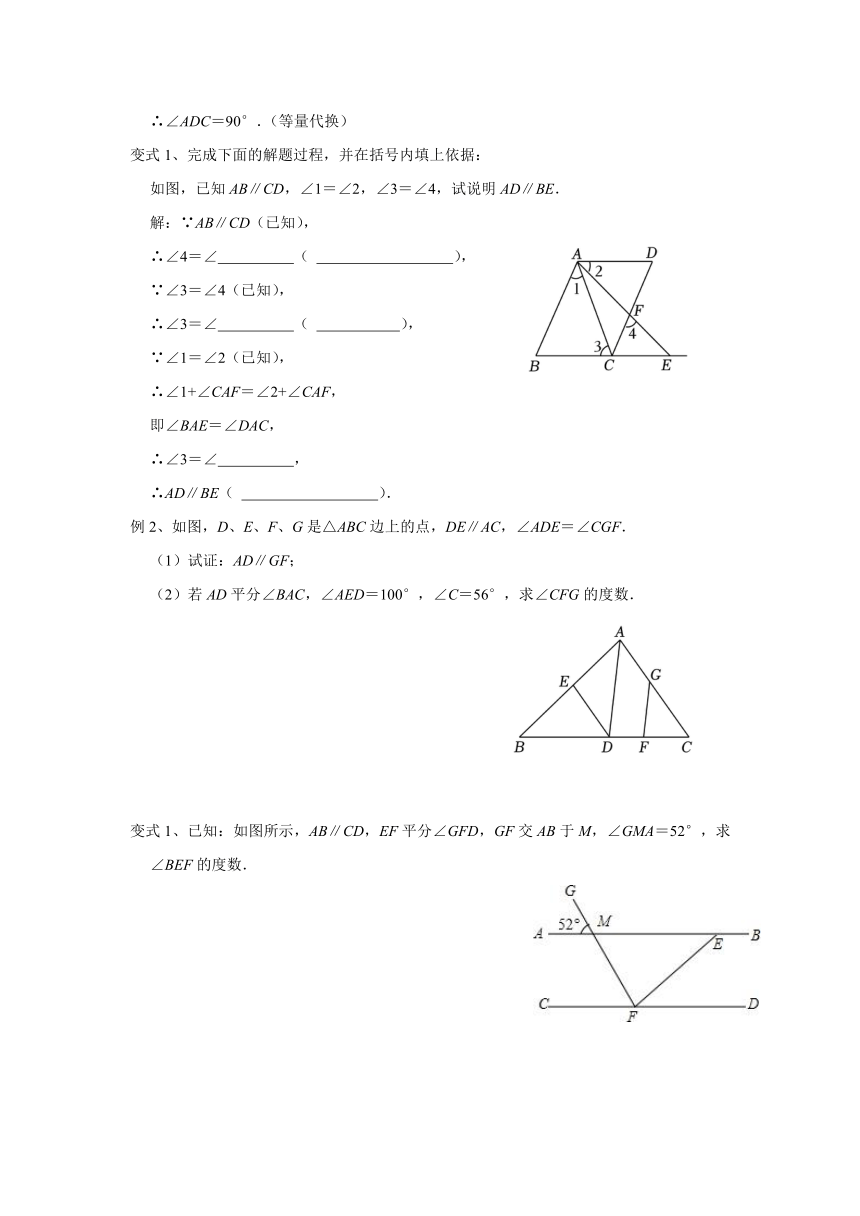
8、如图,将正方形纸片ABCD折叠,使点D落在边AB上的点D′处,点C落在点C′处,若∠AD′M=60°,则∠MNB的度数为( )
A.65° B.70°
C.75° D.80°
一张长方形纸片按如图所示方式折叠后,若∠1=50°,
则∠2= .
10、如图,把一张长方形的纸按图那样折叠后,B,D两点落在B′,D′点处,若∠AOB′=76°,则∠CGO的度数是 .
11、如图,已知AD∥BC,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若α=60°,β=50°,则∠FEM的度数为 ,∠EMF的度数为 .
二、例题精讲:
例1、如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠1=∠C,(已知)
∴GD∥ .( )
∴∠2=∠DAC.( )
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF.( )
∴∠ADC= .(两直线平行,同位角相等)
∵EF⊥BC,(已知)
∴∠EFC=90°.( )
∴∠ADC=90°.(等量代换)
变式1、完成下面的解题过程,并在括号内填上依据:
如图,已知AB∥CD,∠1=∠2,∠3=∠4,试说明AD∥BE.
解:∵AB∥CD(已知),
∴∠4=∠ ( ),
∵∠3=∠4(已知),
∴∠3=∠ ( ),
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF,
即∠BAE=∠DAC,
∴∠3=∠ ,
∴AD∥BE( ).
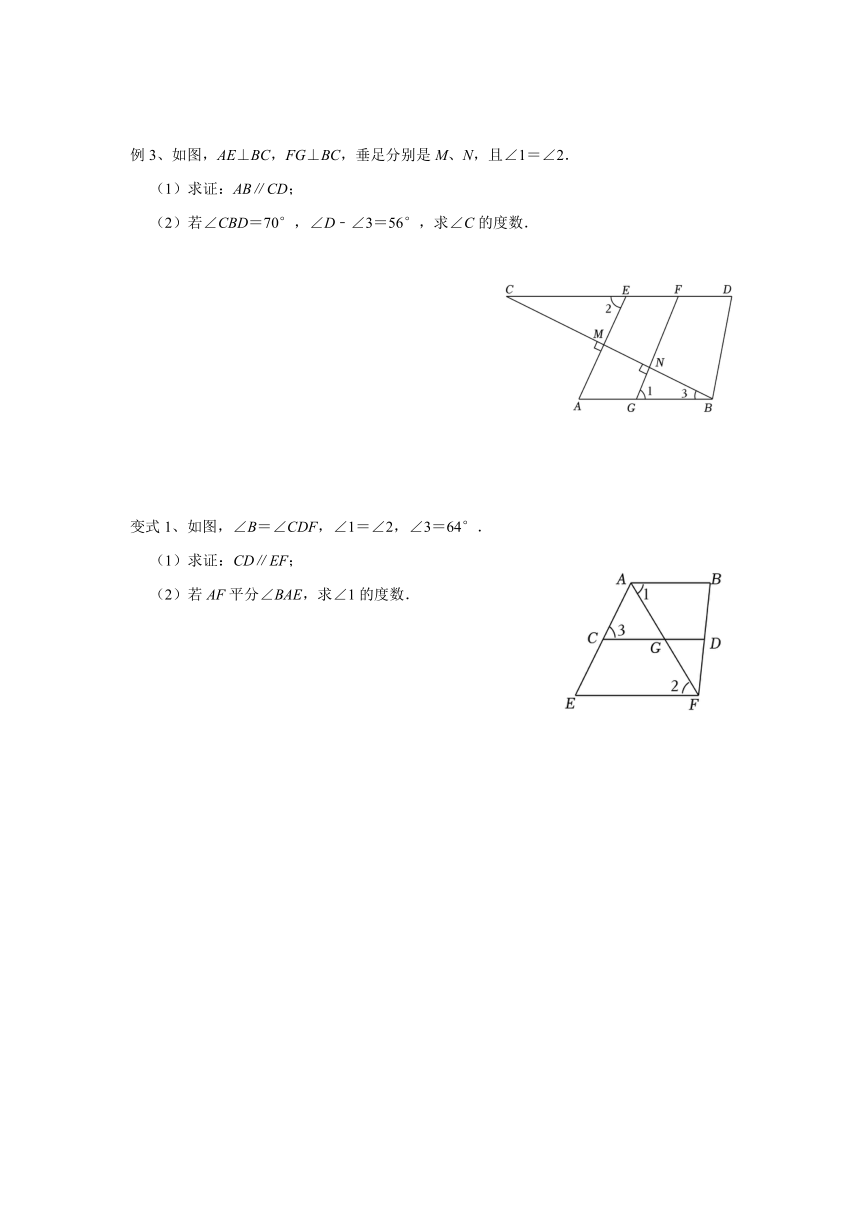
例2、如图,D、E、F、G是△ABC边上的点,DE∥AC,∠ADE=∠CGF.
(1)试证:AD∥GF;
(2)若AD平分∠BAC,∠AED=100°,∠C=56°,求∠CFG的度数.
变式1、已知:如图所示,AB∥CD,EF平分∠GFD,GF交AB于M,∠GMA=52°,求∠BEF的度数.
变式2、如图,在△ABC中,∠A=70°,∠B=50°,CD是∠ACB的平分线,DE∥BC,交AC于点E.
(1)求∠CDE的度数.
(2)若点F为CD中点,连结EF.求证:EF⊥CD.
变式3、如图,在三角形ABC中,点E、点G分别是边AB、AC上的点,点F、点D是边BC上的点,连接EF、AD和DG,DG是∠ADC的角平分线,若∠1+∠2=180°,AB∥DG,∠2=145°,求∠EFC的度数.
变式4、如图,BE是△ABC的角平分线,过E作EF∥AB交△ABC的外角∠CBD的平分线于点F,交边BC于点G.
(1)∠EBF的大小为 度;
(2)求证:G为线段EF的中点.
例3、如图,AE⊥BC,FG⊥BC,垂足分别是M、N,且∠1=∠2.
(1)求证:AB∥CD;
(2)若∠CBD=70°,∠D﹣∠3=56°,求∠C的度数.
变式1、如图,∠B=∠CDF,∠1=∠2,∠3=64°.
(1)求证:CD∥EF;
(2)若AF平分∠BAE,求∠1的度数.
三、能力提升:
1、(1)如图①,若AB∥CD,易证∠B+∠D=∠E.不必证明.
(2)反之,在图①中,若∠B+∠D=∠E,直线AB与CD有什么位置关系?请说明理由.
(3)若将点E移至图②的位置,此时∠B,∠D,∠E之间有什么关系?请说明理由.
(4)在图③中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?(直接写出结论即可)
(5)如图④,AB∥EF,直接写出∠B+∠C+∠D+∠E= .
2、已知:AB∥CD,点E在直线AB、CD之间,连接EA、EC.
(1)如图1,若∠A=80°,∠C=50°,求∠AEC的度数;
(2)如图2,若AF平分∠BAE,CF平分∠DCE交AF于点F,直接写出∠AEC和∠AFC之间的数量关系∠AEC= ;
(3)如图3,在(2)的条件下,延长AE交DC于点G,在AG上取一点K,连接FK交CD于点H,CL⊥AF,若∠CEG=50°,∠AFK=∠CHF.求∠GKH.
3、(1)如图1,已知AB∥CD,∠ABF=∠DCE,求证:∠BFE=∠FEC;
(2)如图2,已知AB∥CD,∠EAF=∠EAB,∠ECF=∠ECD,求证:∠AFC=∠AEC.
4、如图,AE∥BD,∠A=∠BDC,∠AEC的平分线交CD的延长线于点F.
(1)求证:AB∥CD;
(2)探究∠A,∠AEC,∠C之间的数量关系,并说明理由;
(3)若∠BDC=140°,∠F=20°.求∠C的度数.
5、如图,直线AB∥CD,EF∥GH,∠AEF的角平分线交CD于点P.
(1)∠EPF与∠PEF相等吗?请说明理由.
(2)若∠FHG=3∠EPF,求∠EFD的度数.
(3)点Q为射线GH上一点,连结EQ,FQ.若∠QFH=∠FQH,且∠PEQ﹣∠EQF=50°,求∠EQF的度数.
6、(1)已知AB∥CD.
①如图1,求证:∠D=∠E+∠B;
②如图2,F为AB,CD之间一点,连接EF,DF,EG平分∠BEF,FG平分∠EFD,∠D=30°,求∠B,∠G之间的数量关系;
(2)如图3,若AB与CD交于点H,EG平分∠BEF,FG平分∠EFD,∠B﹣∠BHD=20°,∠D=30°,则∠G= °.
7、如图,AB∥CD.
(1)如图1,请探索∠A,∠E,∠C三个角之间的数量关系,并说明理由;
(2)已知∠A=16°.
①如图2,若∠F=100°,求∠C+∠E的度数;
②如图3,若∠AEF和∠DCF的平分线交于点G,请直接写出∠EGC与∠F的数量关系.
8、如图所示,已知l1∥l2,直线AD交l1于A,交l2于D,直线BC交l1于B,交l2于C,AE平分∠BAD,CE平分∠BCD.
(1)试说明∠ADC=2∠BAE;
(2)若∠ADC=70°,∠ABC=36°,求∠AEC的度数.
9、如图,AB∥CD,∠BEH=∠GEH,∠DFK=∠GFK,∠EGF=90°,∠EGF=90°,∠FPQ﹣∠EQP=25°,求n的值.
10、如图,AB∥CD,∠EAF=2∠FAB,∠ECF=2∠FCD,∠AFC=16°,求∠AEC的度数.
夯实基础:
1、平行线的性质:
⑴ 两条直线平行,同位角 .
⑵ 两条直线平行,内错角 .
⑶ 两条直线平行, 同旁内角 .
2、如图,将一张含有30°角的三角形纸片的两个顶点分别叠放在长方形的两条对边上.若∠2=40°,则∠1的度数为( )
A.10° B.20°
C.90°﹣α D.α﹣40°
3、已知直线m∥n,将一块直角三角板按如图所示方式放置,其中三角板的两个顶点分别落在直线m、n上,若∠1=55°,则∠2的度数是( )
A.25° B.30°
C.35° D.40°
4、如图,直线a∥b,∠1=65°,∠B=45°,则∠2的度数为( )
A.105° B.110°
C.117° D.125°
5、如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=48°,那么∠2的度数是( )
A.48° B.78°
C.92° D.102°
6、如图,直线a∥b,将直角三角板的直角顶点放在直线b上,已知∠1=55°,则∠2的度数为( )
A.35° B.45°
C.55° D.125°
7、如图是路政工程车的工作示意图,工作篮底部与支撑平台平行.若∠1=30°,∠2=50°,则∠3的度数为( )
A.130° B.140°
C.150° D.160°
8、如图,将正方形纸片ABCD折叠,使点D落在边AB上的点D′处,点C落在点C′处,若∠AD′M=60°,则∠MNB的度数为( )
A.65° B.70°
C.75° D.80°
一张长方形纸片按如图所示方式折叠后,若∠1=50°,
则∠2= .
10、如图,把一张长方形的纸按图那样折叠后,B,D两点落在B′,D′点处,若∠AOB′=76°,则∠CGO的度数是 .
11、如图,已知AD∥BC,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若α=60°,β=50°,则∠FEM的度数为 ,∠EMF的度数为 .
二、例题精讲:
例1、如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠1=∠C,(已知)
∴GD∥ .( )
∴∠2=∠DAC.( )
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF.( )
∴∠ADC= .(两直线平行,同位角相等)
∵EF⊥BC,(已知)
∴∠EFC=90°.( )
∴∠ADC=90°.(等量代换)
变式1、完成下面的解题过程,并在括号内填上依据:
如图,已知AB∥CD,∠1=∠2,∠3=∠4,试说明AD∥BE.
解:∵AB∥CD(已知),
∴∠4=∠ ( ),
∵∠3=∠4(已知),
∴∠3=∠ ( ),
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF,
即∠BAE=∠DAC,
∴∠3=∠ ,
∴AD∥BE( ).
例2、如图,D、E、F、G是△ABC边上的点,DE∥AC,∠ADE=∠CGF.
(1)试证:AD∥GF;
(2)若AD平分∠BAC,∠AED=100°,∠C=56°,求∠CFG的度数.
变式1、已知:如图所示,AB∥CD,EF平分∠GFD,GF交AB于M,∠GMA=52°,求∠BEF的度数.
变式2、如图,在△ABC中,∠A=70°,∠B=50°,CD是∠ACB的平分线,DE∥BC,交AC于点E.
(1)求∠CDE的度数.
(2)若点F为CD中点,连结EF.求证:EF⊥CD.
变式3、如图,在三角形ABC中,点E、点G分别是边AB、AC上的点,点F、点D是边BC上的点,连接EF、AD和DG,DG是∠ADC的角平分线,若∠1+∠2=180°,AB∥DG,∠2=145°,求∠EFC的度数.
变式4、如图,BE是△ABC的角平分线,过E作EF∥AB交△ABC的外角∠CBD的平分线于点F,交边BC于点G.
(1)∠EBF的大小为 度;
(2)求证:G为线段EF的中点.
例3、如图,AE⊥BC,FG⊥BC,垂足分别是M、N,且∠1=∠2.
(1)求证:AB∥CD;
(2)若∠CBD=70°,∠D﹣∠3=56°,求∠C的度数.
变式1、如图,∠B=∠CDF,∠1=∠2,∠3=64°.
(1)求证:CD∥EF;
(2)若AF平分∠BAE,求∠1的度数.
三、能力提升:
1、(1)如图①,若AB∥CD,易证∠B+∠D=∠E.不必证明.
(2)反之,在图①中,若∠B+∠D=∠E,直线AB与CD有什么位置关系?请说明理由.
(3)若将点E移至图②的位置,此时∠B,∠D,∠E之间有什么关系?请说明理由.
(4)在图③中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?(直接写出结论即可)
(5)如图④,AB∥EF,直接写出∠B+∠C+∠D+∠E= .
2、已知:AB∥CD,点E在直线AB、CD之间,连接EA、EC.
(1)如图1,若∠A=80°,∠C=50°,求∠AEC的度数;
(2)如图2,若AF平分∠BAE,CF平分∠DCE交AF于点F,直接写出∠AEC和∠AFC之间的数量关系∠AEC= ;
(3)如图3,在(2)的条件下,延长AE交DC于点G,在AG上取一点K,连接FK交CD于点H,CL⊥AF,若∠CEG=50°,∠AFK=∠CHF.求∠GKH.
3、(1)如图1,已知AB∥CD,∠ABF=∠DCE,求证:∠BFE=∠FEC;
(2)如图2,已知AB∥CD,∠EAF=∠EAB,∠ECF=∠ECD,求证:∠AFC=∠AEC.
4、如图,AE∥BD,∠A=∠BDC,∠AEC的平分线交CD的延长线于点F.
(1)求证:AB∥CD;
(2)探究∠A,∠AEC,∠C之间的数量关系,并说明理由;
(3)若∠BDC=140°,∠F=20°.求∠C的度数.
5、如图,直线AB∥CD,EF∥GH,∠AEF的角平分线交CD于点P.
(1)∠EPF与∠PEF相等吗?请说明理由.
(2)若∠FHG=3∠EPF,求∠EFD的度数.
(3)点Q为射线GH上一点,连结EQ,FQ.若∠QFH=∠FQH,且∠PEQ﹣∠EQF=50°,求∠EQF的度数.
6、(1)已知AB∥CD.
①如图1,求证:∠D=∠E+∠B;
②如图2,F为AB,CD之间一点,连接EF,DF,EG平分∠BEF,FG平分∠EFD,∠D=30°,求∠B,∠G之间的数量关系;
(2)如图3,若AB与CD交于点H,EG平分∠BEF,FG平分∠EFD,∠B﹣∠BHD=20°,∠D=30°,则∠G= °.
7、如图,AB∥CD.
(1)如图1,请探索∠A,∠E,∠C三个角之间的数量关系,并说明理由;
(2)已知∠A=16°.
①如图2,若∠F=100°,求∠C+∠E的度数;
②如图3,若∠AEF和∠DCF的平分线交于点G,请直接写出∠EGC与∠F的数量关系.
8、如图所示,已知l1∥l2,直线AD交l1于A,交l2于D,直线BC交l1于B,交l2于C,AE平分∠BAD,CE平分∠BCD.
(1)试说明∠ADC=2∠BAE;
(2)若∠ADC=70°,∠ABC=36°,求∠AEC的度数.
9、如图,AB∥CD,∠BEH=∠GEH,∠DFK=∠GFK,∠EGF=90°,∠EGF=90°,∠FPQ﹣∠EQP=25°,求n的值.
10、如图,AB∥CD,∠EAF=2∠FAB,∠ECF=2∠FCD,∠AFC=16°,求∠AEC的度数.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
