17.1 变量与函数 课件(共27张PPT) 2024-2025学年华东师大版数学八年级下册
文档属性
| 名称 | 17.1 变量与函数 课件(共27张PPT) 2024-2025学年华东师大版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 818.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
17.1 变量与函数
学习目标
1.探索简单实例中的数量关系和变化规律,了解常量、变量的意义(重点)
2.了解函数的概念和三种表示法,能用适当的函数表示法表示简单实际问题中变量之间的关系.(重点)
3.能确定简单实际问题中自变量的取值范围,并会求出函数值.(难点)
新课导入
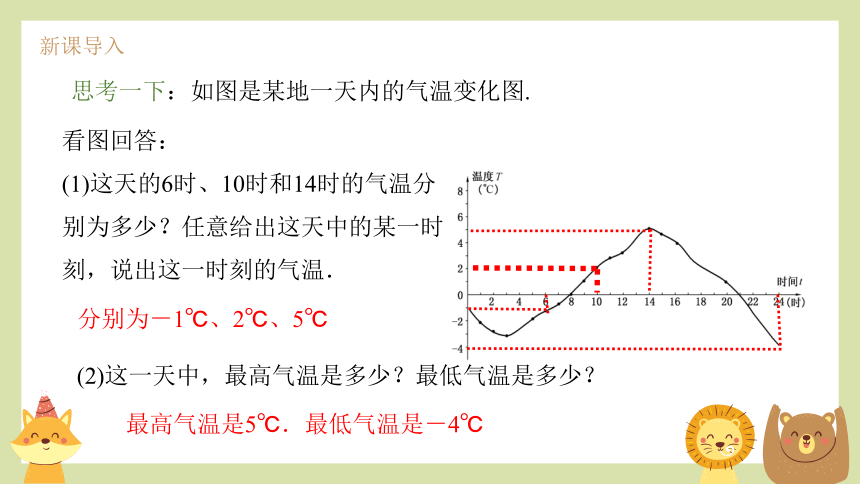
思考一下:如图是某地一天内的气温变化图.
看图回答:
(1)这天的6时、10时和14时的气温分别为多少?任意给出这天中的某一时刻,说出这一时刻的气温.
分别为-1℃、2℃、5℃
(2)这一天中,最高气温是多少?最低气温是多少?
最高气温是5℃.最低气温是-4℃
新课学习
(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低?
这一天中,3时~14时的气温在逐渐升高,0时~3时和14时~24时的气温在逐渐降低
从图中我们可以看到,随着时间t(时)的变化,相应地气温T(℃)也随之变化.那么在生活中是否还有其它类似的数量关系呢?
新课学习
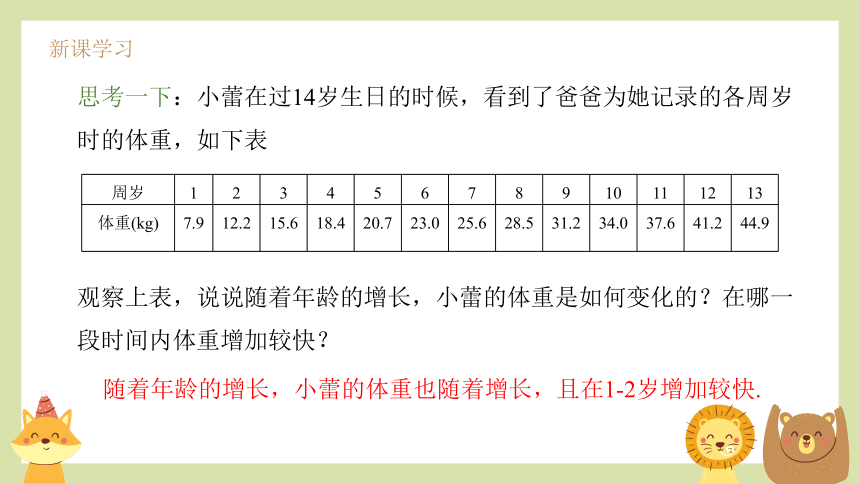
思考一下:小蕾在过14岁生日的时候,看到了爸爸为她记录的各周岁时的体重,如下表
周岁 1 2 3 4 5 6 7 8 9 10 11 12 13
体重(kg) 7.9 12.2 15.6 18.4 20.7 23.0 25.6 28.5 31.2 34.0 37.6 41.2 44.9
观察上表,说说随着年龄的增长,小蕾的体重是如何变化的?在哪一段时间内体重增加较快?
随着年龄的增长,小蕾的体重也随着增长,且在1-2岁增加较快.
新课学习
思考一下:收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值:
波长λ(m) 300 500 600 1 000 1 500
频率f(kHz) 1 000 600 500 300 200
观察上表回答:
(1)波长l和频率f数值之间有什么关系
λ与 f 的乘积是一个定值,即λf=300 000,或者
300 000
λ
f =
(2)波长λ越大,频率f 就_____
越小
新课学习
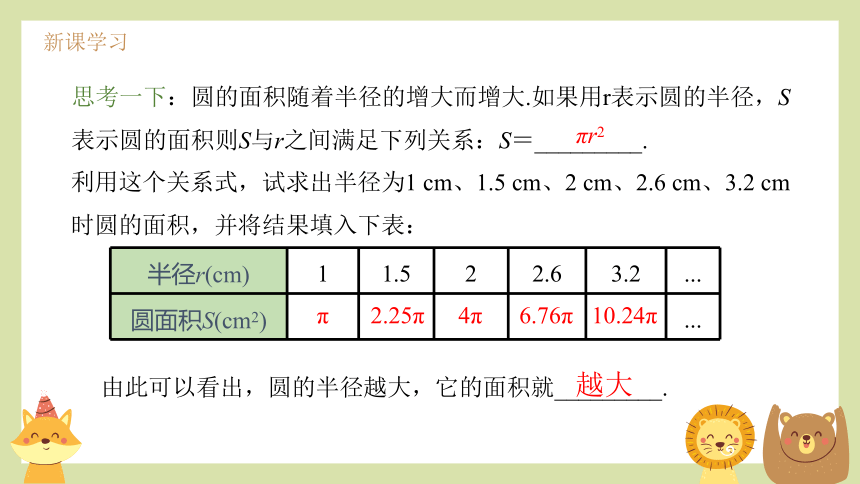
思考一下:圆的面积随着半径的增大而增大.如果用r表示圆的半径,S表示圆的面积则S与r之间满足下列关系:S=_________.
πr2
利用这个关系式,试求出半径为1 cm、1.5 cm、2 cm、2.6 cm、3.2 cm时圆的面积,并将结果填入下表:
半径r(cm) 1 1.5 2 2.6 3.2 ...
圆面积S(cm2) ...
π
2.25π
4π
6.76π
10.24π
越大
由此可以看出,圆的半径越大,它的面积就_________.
新课学习
变量的概念
在某一变化过程中,可以取不同数值的量,叫做变量.
常量的概念
在某一变化过程中,取值始终保持不变的量,叫做常量.即数值始终不变的量为常量.
新课学习
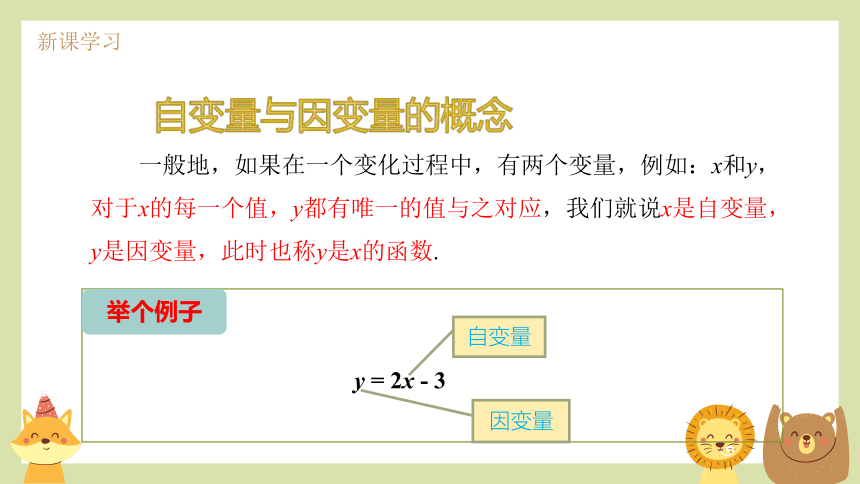
自变量与因变量的概念
一般地,如果在一个变化过程中,有两个变量,例如:x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.
举个例子
y = 2x - 3
自变量
因变量
新课学习
例1 以下各式中,y是x的函数的有:
y=5不含未知数x,故 y=5不属于y是x的函数
√
√
×
×
判断一个变量是否是另一个变量的函数,关键是看当一个变量确定时,另一个变量是否有唯一确定的值与它对应.
新课学习
表示函数关系的方法通常有三种
(1)解析法,如问题4中的S=π r2,这个表达式称为函数的关系式.
(2)列表法,如问题2中的小蕾的体重表,问题3中的波长与频率关系表.
(3)图象法,如问题1中的气温曲线.
新课学习
拓展:函数关系的三种方法的优缺点
表示方法 优点 缺点
解析法
列表法
图象法
能准确地反映整个变化过程中自变量与因变量的对应关系
(1)求对应的函数值时,要经过计算;(2)有些函数关系不能用表达式表示出来
(1)列出的对应值有限;(2)在表格中不容易看出自变量与因变量的变化趋势
由自变量的值常常难以准确找到其对应的函数值
一目了然,对表格中已有自变量的每个值可直接査出与它对应的函数值.
直观、形象地反映出函数关系变化的趋 势和某些性质.
新课学习
试一试:(1)填写如图所示10以内正整数的加法表,然后把所有填有10的格子涂黑,看看你能发现什么
1
1
2
3
4
5
6
7
8
10
11
9
2
3
4
5
6
7
8
10
11
9
5
6
2
+
横向的加数与纵向的加数之和为10;
涂黑的格子在一条直线上
新课学习
(2)如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,y是x的函数,那么y和x之间的函数关系式是 .
1
1
2
3
4
5
6
7
8
10
11
9
2
3
4
5
6
7
8
10
11
9
5
6
2
+
y=10-x
(3)当涂黑的格子横向的加数为3时,纵向的加数是___,当纵向的加数为6时,横向的加数是___.
7
4
新课学习
例2 等腰三角形顶角的度数y是底角度数x的函数,试写出这个函数关系式,并求出自变量x的取值范围.
y
x
根据等腰三角形的性质和三角形内角和定理,可知
2x+y=180°
有 y=180°-2x
由于等腰三角形的底角只能是锐角,所以自变量的取值范围是
0°新课学习
例3 等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10 cm,CA与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.
(1)试写出重叠部分面积y(cm2)与线段MA长度x(cm)之间的函数关系式.
分析:根据图形及题意所述可得出重叠部分是等腰直角三角形,从而根据MA的长度可得出y与x的关系
新课学习
(1)试写出重叠部分面积y(cm2)与线段MA长度x(cm)之间的函数关系式
M
Q
N
P
A
B
C
x
x
重叠部分面积 y与线段MA长度 x之间的函数关系式为
新课学习
(2)当A点向右移动1 cm时,重叠部分的面积是多少
分析:将x=1cm代入,可得出重叠部分的面积
点A向右移动1cm,即x=1
所以当点A向右移动1cm时,重叠部分的面积为0.5 cm2.
课堂巩固
C
课堂巩固
C
课堂巩固
D
课堂巩固
D
课堂巩固
课堂巩固
B
课堂巩固
课堂总结
1.变量与常量的概念
2.自变量与因变量的概念
3.表示函数关系的方法通常有三种
感谢同学们的观看
Thank You For Watching
17.1 变量与函数
学习目标
1.探索简单实例中的数量关系和变化规律,了解常量、变量的意义(重点)
2.了解函数的概念和三种表示法,能用适当的函数表示法表示简单实际问题中变量之间的关系.(重点)
3.能确定简单实际问题中自变量的取值范围,并会求出函数值.(难点)
新课导入
思考一下:如图是某地一天内的气温变化图.
看图回答:
(1)这天的6时、10时和14时的气温分别为多少?任意给出这天中的某一时刻,说出这一时刻的气温.
分别为-1℃、2℃、5℃
(2)这一天中,最高气温是多少?最低气温是多少?
最高气温是5℃.最低气温是-4℃
新课学习
(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低?
这一天中,3时~14时的气温在逐渐升高,0时~3时和14时~24时的气温在逐渐降低
从图中我们可以看到,随着时间t(时)的变化,相应地气温T(℃)也随之变化.那么在生活中是否还有其它类似的数量关系呢?
新课学习
思考一下:小蕾在过14岁生日的时候,看到了爸爸为她记录的各周岁时的体重,如下表
周岁 1 2 3 4 5 6 7 8 9 10 11 12 13
体重(kg) 7.9 12.2 15.6 18.4 20.7 23.0 25.6 28.5 31.2 34.0 37.6 41.2 44.9
观察上表,说说随着年龄的增长,小蕾的体重是如何变化的?在哪一段时间内体重增加较快?
随着年龄的增长,小蕾的体重也随着增长,且在1-2岁增加较快.
新课学习
思考一下:收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值:
波长λ(m) 300 500 600 1 000 1 500
频率f(kHz) 1 000 600 500 300 200
观察上表回答:
(1)波长l和频率f数值之间有什么关系
λ与 f 的乘积是一个定值,即λf=300 000,或者
300 000
λ
f =
(2)波长λ越大,频率f 就_____
越小
新课学习
思考一下:圆的面积随着半径的增大而增大.如果用r表示圆的半径,S表示圆的面积则S与r之间满足下列关系:S=_________.
πr2
利用这个关系式,试求出半径为1 cm、1.5 cm、2 cm、2.6 cm、3.2 cm时圆的面积,并将结果填入下表:
半径r(cm) 1 1.5 2 2.6 3.2 ...
圆面积S(cm2) ...
π
2.25π
4π
6.76π
10.24π
越大
由此可以看出,圆的半径越大,它的面积就_________.
新课学习
变量的概念
在某一变化过程中,可以取不同数值的量,叫做变量.
常量的概念
在某一变化过程中,取值始终保持不变的量,叫做常量.即数值始终不变的量为常量.
新课学习
自变量与因变量的概念
一般地,如果在一个变化过程中,有两个变量,例如:x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.
举个例子
y = 2x - 3
自变量
因变量
新课学习
例1 以下各式中,y是x的函数的有:
y=5不含未知数x,故 y=5不属于y是x的函数
√
√
×
×
判断一个变量是否是另一个变量的函数,关键是看当一个变量确定时,另一个变量是否有唯一确定的值与它对应.
新课学习
表示函数关系的方法通常有三种
(1)解析法,如问题4中的S=π r2,这个表达式称为函数的关系式.
(2)列表法,如问题2中的小蕾的体重表,问题3中的波长与频率关系表.
(3)图象法,如问题1中的气温曲线.
新课学习
拓展:函数关系的三种方法的优缺点
表示方法 优点 缺点
解析法
列表法
图象法
能准确地反映整个变化过程中自变量与因变量的对应关系
(1)求对应的函数值时,要经过计算;(2)有些函数关系不能用表达式表示出来
(1)列出的对应值有限;(2)在表格中不容易看出自变量与因变量的变化趋势
由自变量的值常常难以准确找到其对应的函数值
一目了然,对表格中已有自变量的每个值可直接査出与它对应的函数值.
直观、形象地反映出函数关系变化的趋 势和某些性质.
新课学习
试一试:(1)填写如图所示10以内正整数的加法表,然后把所有填有10的格子涂黑,看看你能发现什么
1
1
2
3
4
5
6
7
8
10
11
9
2
3
4
5
6
7
8
10
11
9
5
6
2
+
横向的加数与纵向的加数之和为10;
涂黑的格子在一条直线上
新课学习
(2)如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,y是x的函数,那么y和x之间的函数关系式是 .
1
1
2
3
4
5
6
7
8
10
11
9
2
3
4
5
6
7
8
10
11
9
5
6
2
+
y=10-x
(3)当涂黑的格子横向的加数为3时,纵向的加数是___,当纵向的加数为6时,横向的加数是___.
7
4
新课学习
例2 等腰三角形顶角的度数y是底角度数x的函数,试写出这个函数关系式,并求出自变量x的取值范围.
y
x
根据等腰三角形的性质和三角形内角和定理,可知
2x+y=180°
有 y=180°-2x
由于等腰三角形的底角只能是锐角,所以自变量的取值范围是
0°
例3 等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10 cm,CA与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.
(1)试写出重叠部分面积y(cm2)与线段MA长度x(cm)之间的函数关系式.
分析:根据图形及题意所述可得出重叠部分是等腰直角三角形,从而根据MA的长度可得出y与x的关系
新课学习
(1)试写出重叠部分面积y(cm2)与线段MA长度x(cm)之间的函数关系式
M
Q
N
P
A
B
C
x
x
重叠部分面积 y与线段MA长度 x之间的函数关系式为
新课学习
(2)当A点向右移动1 cm时,重叠部分的面积是多少
分析:将x=1cm代入,可得出重叠部分的面积
点A向右移动1cm,即x=1
所以当点A向右移动1cm时,重叠部分的面积为0.5 cm2.
课堂巩固
C
课堂巩固
C
课堂巩固
D
课堂巩固
D
课堂巩固
课堂巩固
B
课堂巩固
课堂总结
1.变量与常量的概念
2.自变量与因变量的概念
3.表示函数关系的方法通常有三种
感谢同学们的观看
Thank You For Watching
