16.1.2 分式的基本性质 课件(共28张PPT) 2024-2025学年华东师大版初中数学八年级下册
文档属性
| 名称 | 16.1.2 分式的基本性质 课件(共28张PPT) 2024-2025学年华东师大版初中数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 600.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 12:01:45 | ||
图片预览





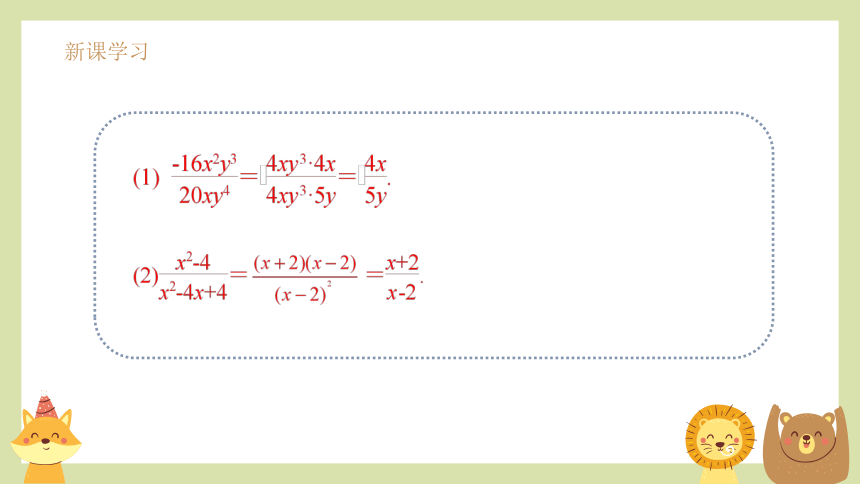



文档简介
(共28张PPT)
16.1.2 分式的基本性质
学习目标
1.运用分式的基本性质进行分式的约分和通分.(重点)
2.灵活运用分式的基本性质将分式变形.(难点)
新课导入
思考下面的问题
这几个分数有什么关系?
第二个分数分子、分母除以2等于第一个分数,最后一个分数分子、分母除以a等于第一个分数
新课学习
分式的基本性质
分式的分子与分母都乘以(或都除以)同一个不等于零的整式,分式的值不变.
新课学习
例3 约分:
分析:分式的约分,即要求把分子与分母的公因式约去.为此,首先要找出分子与分母的公因式.
新课学习
新课学习
最简分式的概念
约分后,分子与分母不再有公因式.分子与分母没有公因式的分式称为最简分式.
新课学习
思考一下:约分的关键是什么?
约分是应用分式的基本性质把分式的分子、分母同除以同一个整式,使分式的值不变.所以要找准分子和分母的公因式,约分的结果要是最简分式.
新课学习
(1)若分子﹑分母都是单项式,则约去系数的最大公约数,并约去相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母所有的公因式.
拓展:约分的基本步骤
新课学习
不可以
为什么这两个分式不可以化成同分母分式,什么样的两个分式可以化成同分母分式?
新课学习
通分的概念
分式的通分,即要求把几个异分母的分式分别化为与原来的分式相等的同分母的分式
新课学习
最简公分母的概念
各分式所有因式的最高次幂的积作为公分母,叫做最简公分母
注意:确定最简公分母是通分的关键
新课学习
例4 通分:
最简公分母
最简公分母是a2b2
新课学习
最简公分母
x2
-y2
最简公分母是x2-y2
新课学习
最简公分母
x(x-y)
(x+y)
最简公分母是x3-xy2
(x-y)(x+y)
x(x+y)
课堂巩固
D
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
(x+y)2(x-y)
课堂总结
1.分式的基本性质
2.最简分式的概念
3.通分的概念
4.最简分母的概念
感谢同学们的观看
Thank You For Watching
16.1.2 分式的基本性质
学习目标
1.运用分式的基本性质进行分式的约分和通分.(重点)
2.灵活运用分式的基本性质将分式变形.(难点)
新课导入
思考下面的问题
这几个分数有什么关系?
第二个分数分子、分母除以2等于第一个分数,最后一个分数分子、分母除以a等于第一个分数
新课学习
分式的基本性质
分式的分子与分母都乘以(或都除以)同一个不等于零的整式,分式的值不变.
新课学习
例3 约分:
分析:分式的约分,即要求把分子与分母的公因式约去.为此,首先要找出分子与分母的公因式.
新课学习
新课学习
最简分式的概念
约分后,分子与分母不再有公因式.分子与分母没有公因式的分式称为最简分式.
新课学习
思考一下:约分的关键是什么?
约分是应用分式的基本性质把分式的分子、分母同除以同一个整式,使分式的值不变.所以要找准分子和分母的公因式,约分的结果要是最简分式.
新课学习
(1)若分子﹑分母都是单项式,则约去系数的最大公约数,并约去相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母所有的公因式.
拓展:约分的基本步骤
新课学习
不可以
为什么这两个分式不可以化成同分母分式,什么样的两个分式可以化成同分母分式?
新课学习
通分的概念
分式的通分,即要求把几个异分母的分式分别化为与原来的分式相等的同分母的分式
新课学习
最简公分母的概念
各分式所有因式的最高次幂的积作为公分母,叫做最简公分母
注意:确定最简公分母是通分的关键
新课学习
例4 通分:
最简公分母
最简公分母是a2b2
新课学习
最简公分母
x2
-y2
最简公分母是x2-y2
新课学习
最简公分母
x(x-y)
(x+y)
最简公分母是x3-xy2
(x-y)(x+y)
x(x+y)
课堂巩固
D
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
(x+y)2(x-y)
课堂总结
1.分式的基本性质
2.最简分式的概念
3.通分的概念
4.最简分母的概念
感谢同学们的观看
Thank You For Watching
