4.2 全等三角形 课件(共24张PPT) 2024-2025学年北师大版初中数学七年级下册
文档属性
| 名称 | 4.2 全等三角形 课件(共24张PPT) 2024-2025学年北师大版初中数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 16.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
第四章 三角形
4.2 全等三角形
1.理解全等三角形的概念及其表示方法.
2.能够准确找出全等三角形的对应元素.
3.掌握全等三角形的性质,并能进行简单的推理和计算.
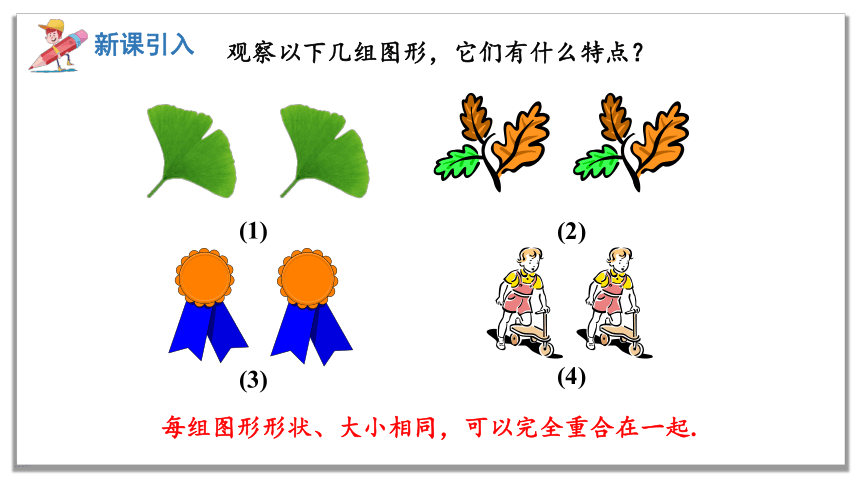
观察以下几组图形,它们有什么特点?
每组图形形状、大小相同,可以完全重合在一起.
(1)
(2)
(3)
(4)
在生活中,我们会看到完全一样的图形,如果把它们叠在一起,它们就能够完全重合. 你能看出来下列图片中的哪些三角形可以完全重合吗
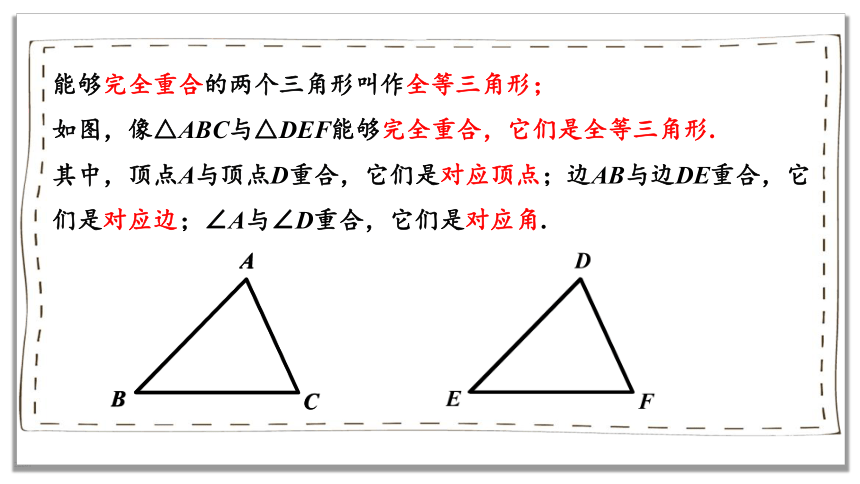
能够完全重合的两个三角形叫作全等三角形;
如图,像△ABC与△DEF能够完全重合,它们是全等三角形.
其中,顶点A与顶点D重合,它们是对应顶点;边AB与边DE重合,它们是对应边;∠A与∠D重合,它们是对应角.
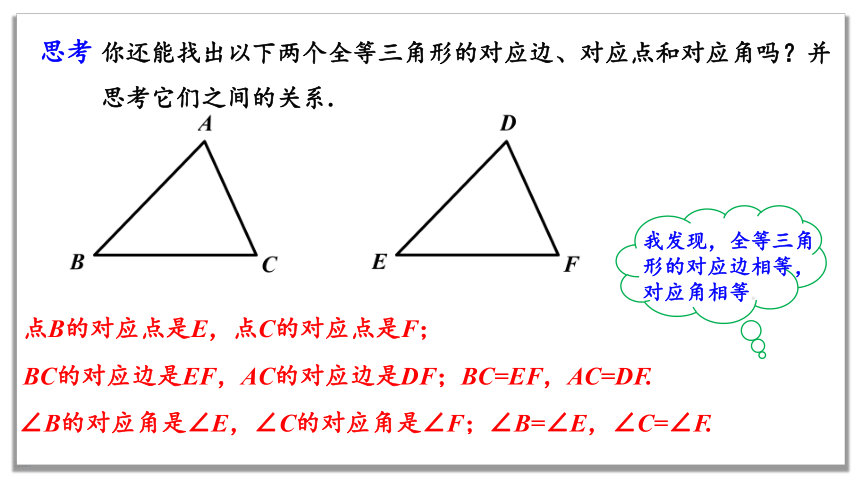
思考
你还能找出以下两个全等三角形的对应边、对应点和对应角吗?并思考它们之间的关系.
点B的对应点是E,点C的对应点是F;
BC的对应边是EF,AC的对应边是DF;BC=EF,AC=DF.
∠B的对应角是∠E,∠C的对应角是∠F;∠B=∠E,∠C=∠F.
我发现,全等三角形的对应边相等,对应角相等.
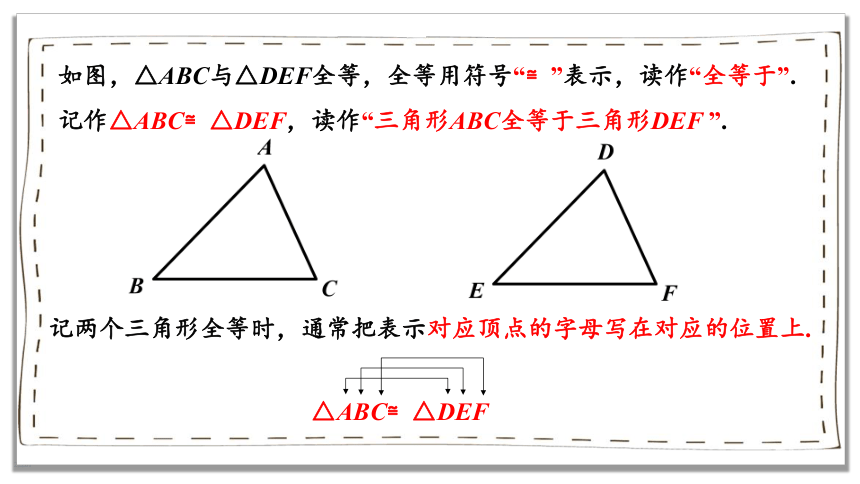
如图,△ABC与△DEF全等,全等用符号“≌”表示,读作“全等于”. 记作△ABC≌△DEF,读作“三角形ABC全等于三角形DEF ”.
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
△ABC≌△DEF
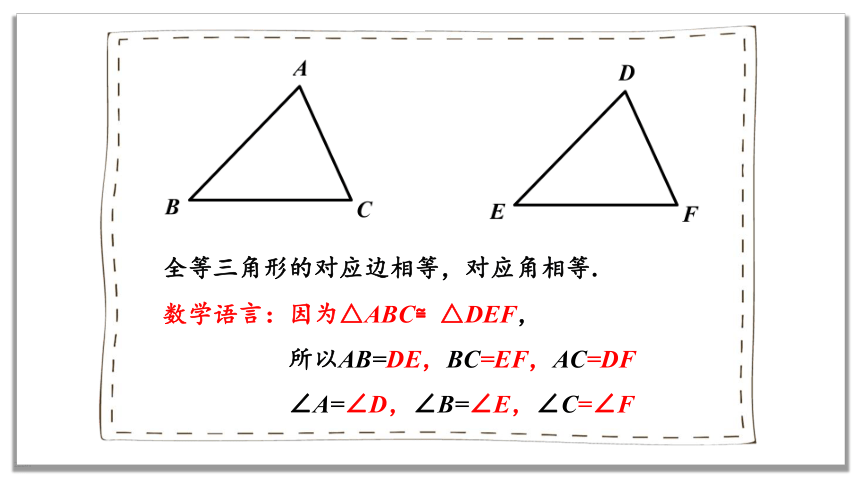
数学语言:因为△ABC≌△DEF,
所以AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形的对应边相等,对应角相等.
温馨提示
寻找全等三角形对应边、对应角的三种方法:
字母顺序法 根据书写规范,按照对应顶点确定对应边、对应角.
位置关系法 公共角(对顶角)为对应角,公共边为对应边;
对应角的对边为对应边,对应边的对角为对应角.
图形特征法 最长边对最长边,最短边对最短边;
最大角对最大角,最小角对最小角.
例1 如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠E的度数和CF的长.
解:因为△ABC≌△DEF,∠A=70°,
∠B=50°,BF=4,EF=7,
所以∠E=∠B= 50°,BC=EF= 7,
所以CF=BC – BF =7 – 4= 3.
(1)每人准备两个全等三角形纸片,并画出两个三角形纸片对应边的高. 全等三角形对应边的高相等吗 对应边的中线呢 对应的角平分线呢
B
A
C
D
E
F
操作·交流
如图,△ABC≌△DEF,边BC与边EF是对应边,对应边上的高AM与DN相等,中线AQ与DS相等,对应角∠A与∠D的平分线AO与DP相等.
全等三角形对应边的高、中线、角平分线分别相等.
B
A
C
D
E
F
M
N
O
Q
P
S
(2)如图,已知△ABC≌△A'B'C',点D,E分别在BC边、AB边上,请在△A'B'C'中画出与线段DE相对应的线段. 图中有哪些相等的线段、相等的角?与同伴进行交流.
作法:①在A'B'上截取A'E'=AE,B'C'上截取B'D'=BD,找到E、D的对应点E'、D';
②连接E'、D',E'D'即为ED的对应线段.
D'
E'
试着和同伴找一找图中相等的线段和角吧!
准备一张等边三角形纸片,你能用折纸的办法把它分成两个全等三角形吗 能把它分成三个全等三角形吗 能把它分成四个全等三角形吗 与同伴进行交流.
得到两个全等三角形.
尝试·交流
沿着这三条折痕折叠,便可得到三个全等三角形.
想一想,怎样折纸把它分成四个全等三角形?
1. 如图所示的两个三角形能够完全重合,则下列表示正确的是( B )
A. △ABC≌△CBD B. △ABC≌△DBC
C. △ABC≌△DCB D. △ABC≌△CDB
B
2. 如图,将△ABC沿AD所在直线对折,△ABD和△ACD完全重合,则△ABD≌ ________,AB的对应边是 ______,AD的对应边是 ______,∠BAD的对应角是 ______.
△ACD
AC
AD
∠CAD
3. 如图,△ABC与△ADC全等,请用数学符号表示出这两个三角形全等,并写出相等的边和角.
解:△ABC≌△ADC;
相等的边为:AB = AD,AC = AC,BC = DC;
相等的角为:∠BAC=∠DAC,∠B=∠D,∠ACB=∠ACD.
4.如图,△ABC≌△AED,∠BAC=25°,∠B= 35°,AB=3cm,BC=1cm,求出∠E,∠ADE的度数和线段DE,AE 的长度.
B
C
E
D
A
解: 因为 △ABC≌△AED(已知)
所以∠E =∠B = 35°(全等三角形对应角相等)
∠ADE =∠ACB=180°- 25°- 35°= 120 ° (全等三角形对应角相等)
DE = BC = 1cm, AE = AB = 3cm. (全等三角形对应边相等)
5.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)试说明:BD=DE+CE;
B
E
D
A
C
解:因为△BAD≌△ACE,
所以AD = CE,BD = AE,
因为A,D,E三点在同一直线上,
所以AE = AD + DE,
所以BD = CE + DE;
5.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(2)请你猜想△ABD满足什么条件时,BD∥CE.
B
E
D
A
C
解:当∠ADB = 90°时,BD∥CE,
因为△BAD≌△ACE,
所以∠ADB = ∠E = 90°,
所以∠BDE = 90°
所以BD∥CE.(内错角相等,两直线平行)
6.如图,△ABC≌△ADE,∠CAD=10°,∠B=∠D=25°,∠EAB=120°.求∠AED的度数.
A
B
C
E
D
解:因为△ABC≌△ADE ;
所以∠EAD=∠CAB .
因为∠CAD=10°,∠EAB=120°;
所以∠EAD=
因为∠B=∠D=25°;
所以∠AED=180°- ∠EAD- ∠D =180°- 55°- 25°=100°.
全等
三角形
定义
能够完全重合的两个三角形叫作全等三角形.
如图,像△ABC与△DEF能够完全重合,它们是全等三角形.
性质
数学语言:因为△ABC≌△DEF,
所以AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形的对应边相等,对应角相等.
第四章 三角形
4.2 全等三角形
1.理解全等三角形的概念及其表示方法.
2.能够准确找出全等三角形的对应元素.
3.掌握全等三角形的性质,并能进行简单的推理和计算.
观察以下几组图形,它们有什么特点?
每组图形形状、大小相同,可以完全重合在一起.
(1)
(2)
(3)
(4)
在生活中,我们会看到完全一样的图形,如果把它们叠在一起,它们就能够完全重合. 你能看出来下列图片中的哪些三角形可以完全重合吗
能够完全重合的两个三角形叫作全等三角形;
如图,像△ABC与△DEF能够完全重合,它们是全等三角形.
其中,顶点A与顶点D重合,它们是对应顶点;边AB与边DE重合,它们是对应边;∠A与∠D重合,它们是对应角.
思考
你还能找出以下两个全等三角形的对应边、对应点和对应角吗?并思考它们之间的关系.
点B的对应点是E,点C的对应点是F;
BC的对应边是EF,AC的对应边是DF;BC=EF,AC=DF.
∠B的对应角是∠E,∠C的对应角是∠F;∠B=∠E,∠C=∠F.
我发现,全等三角形的对应边相等,对应角相等.
如图,△ABC与△DEF全等,全等用符号“≌”表示,读作“全等于”. 记作△ABC≌△DEF,读作“三角形ABC全等于三角形DEF ”.
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
△ABC≌△DEF
数学语言:因为△ABC≌△DEF,
所以AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形的对应边相等,对应角相等.
温馨提示
寻找全等三角形对应边、对应角的三种方法:
字母顺序法 根据书写规范,按照对应顶点确定对应边、对应角.
位置关系法 公共角(对顶角)为对应角,公共边为对应边;
对应角的对边为对应边,对应边的对角为对应角.
图形特征法 最长边对最长边,最短边对最短边;
最大角对最大角,最小角对最小角.
例1 如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠E的度数和CF的长.
解:因为△ABC≌△DEF,∠A=70°,
∠B=50°,BF=4,EF=7,
所以∠E=∠B= 50°,BC=EF= 7,
所以CF=BC – BF =7 – 4= 3.
(1)每人准备两个全等三角形纸片,并画出两个三角形纸片对应边的高. 全等三角形对应边的高相等吗 对应边的中线呢 对应的角平分线呢
B
A
C
D
E
F
操作·交流
如图,△ABC≌△DEF,边BC与边EF是对应边,对应边上的高AM与DN相等,中线AQ与DS相等,对应角∠A与∠D的平分线AO与DP相等.
全等三角形对应边的高、中线、角平分线分别相等.
B
A
C
D
E
F
M
N
O
Q
P
S
(2)如图,已知△ABC≌△A'B'C',点D,E分别在BC边、AB边上,请在△A'B'C'中画出与线段DE相对应的线段. 图中有哪些相等的线段、相等的角?与同伴进行交流.
作法:①在A'B'上截取A'E'=AE,B'C'上截取B'D'=BD,找到E、D的对应点E'、D';
②连接E'、D',E'D'即为ED的对应线段.
D'
E'
试着和同伴找一找图中相等的线段和角吧!
准备一张等边三角形纸片,你能用折纸的办法把它分成两个全等三角形吗 能把它分成三个全等三角形吗 能把它分成四个全等三角形吗 与同伴进行交流.
得到两个全等三角形.
尝试·交流
沿着这三条折痕折叠,便可得到三个全等三角形.
想一想,怎样折纸把它分成四个全等三角形?
1. 如图所示的两个三角形能够完全重合,则下列表示正确的是( B )
A. △ABC≌△CBD B. △ABC≌△DBC
C. △ABC≌△DCB D. △ABC≌△CDB
B
2. 如图,将△ABC沿AD所在直线对折,△ABD和△ACD完全重合,则△ABD≌ ________,AB的对应边是 ______,AD的对应边是 ______,∠BAD的对应角是 ______.
△ACD
AC
AD
∠CAD
3. 如图,△ABC与△ADC全等,请用数学符号表示出这两个三角形全等,并写出相等的边和角.
解:△ABC≌△ADC;
相等的边为:AB = AD,AC = AC,BC = DC;
相等的角为:∠BAC=∠DAC,∠B=∠D,∠ACB=∠ACD.
4.如图,△ABC≌△AED,∠BAC=25°,∠B= 35°,AB=3cm,BC=1cm,求出∠E,∠ADE的度数和线段DE,AE 的长度.
B
C
E
D
A
解: 因为 △ABC≌△AED(已知)
所以∠E =∠B = 35°(全等三角形对应角相等)
∠ADE =∠ACB=180°- 25°- 35°= 120 ° (全等三角形对应角相等)
DE = BC = 1cm, AE = AB = 3cm. (全等三角形对应边相等)
5.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)试说明:BD=DE+CE;
B
E
D
A
C
解:因为△BAD≌△ACE,
所以AD = CE,BD = AE,
因为A,D,E三点在同一直线上,
所以AE = AD + DE,
所以BD = CE + DE;
5.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(2)请你猜想△ABD满足什么条件时,BD∥CE.
B
E
D
A
C
解:当∠ADB = 90°时,BD∥CE,
因为△BAD≌△ACE,
所以∠ADB = ∠E = 90°,
所以∠BDE = 90°
所以BD∥CE.(内错角相等,两直线平行)
6.如图,△ABC≌△ADE,∠CAD=10°,∠B=∠D=25°,∠EAB=120°.求∠AED的度数.
A
B
C
E
D
解:因为△ABC≌△ADE ;
所以∠EAD=∠CAB .
因为∠CAD=10°,∠EAB=120°;
所以∠EAD=
因为∠B=∠D=25°;
所以∠AED=180°- ∠EAD- ∠D =180°- 55°- 25°=100°.
全等
三角形
定义
能够完全重合的两个三角形叫作全等三角形.
如图,像△ABC与△DEF能够完全重合,它们是全等三角形.
性质
数学语言:因为△ABC≌△DEF,
所以AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形的对应边相等,对应角相等.
同课章节目录
