4.3 课时1 利用“边边边”判定三角形全等 课件(共24张PPT) 2024-2025学年北师大版初中数学七年级下册
文档属性
| 名称 | 4.3 课时1 利用“边边边”判定三角形全等 课件(共24张PPT) 2024-2025学年北师大版初中数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
第四章 三角形
4.3 课时1 利用“边边边”
判定三角形全等
1.理解并且会用“边边边”来判断三角形全等.
2.了解三角形的稳定性.
要画一个三角形,使它与小明画的三角形全等,你会怎么画呢
想一想,动手画一画吧!
要画一个与已知三角形全等的三角形,至少需要几个与边或角的大小有关的条件
我猜测至少需要三个与边或角的大小有关的条件.
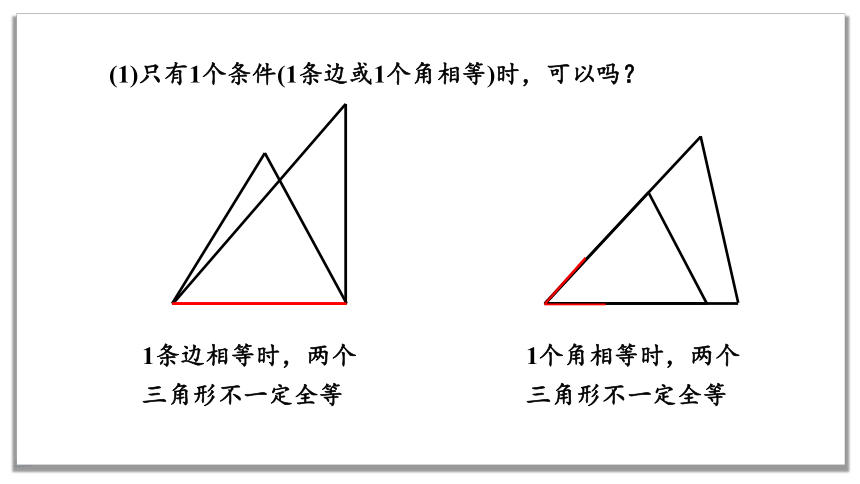
(1)只有1个条件(1条边或1个角相等)时,可以吗?
1条边相等时,两个三角形不一定全等
1个角相等时,两个三角形不一定全等
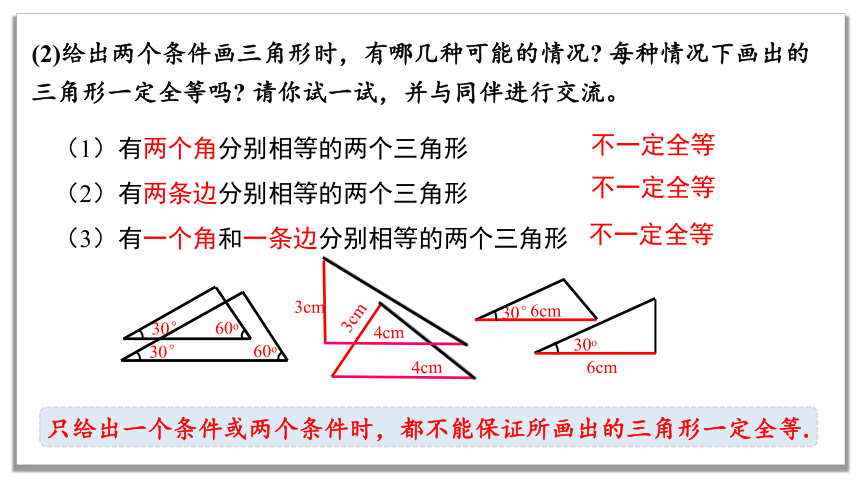
(2)给出两个条件画三角形时,有哪几种可能的情况 每种情况下画出的三角形一定全等吗 请你试一试,并与同伴进行交流。
只给出一个条件或两个条件时,都不能保证所画出的三角形一定全等.
不一定全等
不一定全等
不一定全等
6cm
30°
3cm
4cm
3cm
4cm
30o
6cm
60o
30°
30°
60o
(1)有两个角分别相等的两个三角形
(2)有两条边分别相等的两个三角形
(3)有一个角和一条边分别相等的两个三角形
给出三个条件画三角形,有哪几种可能的情况?与同伴进行交流.
(1)三个角都相等;
(2)三条边都相等;
(3)两边和一角相等;
(4)两角和一边相等.
思考·交流
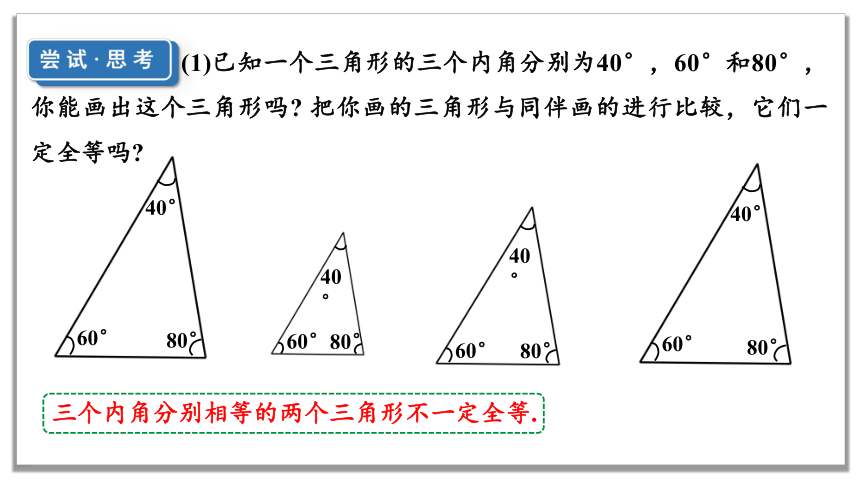
(1)已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗 把你画的三角形与同伴画的进行比较,它们一定全等吗
40°
60°
80°
40°
60°
80°
40°
60°
80°
40°
60°
80°
三个内角分别相等的两个三角形不一定全等.
尝试·思考
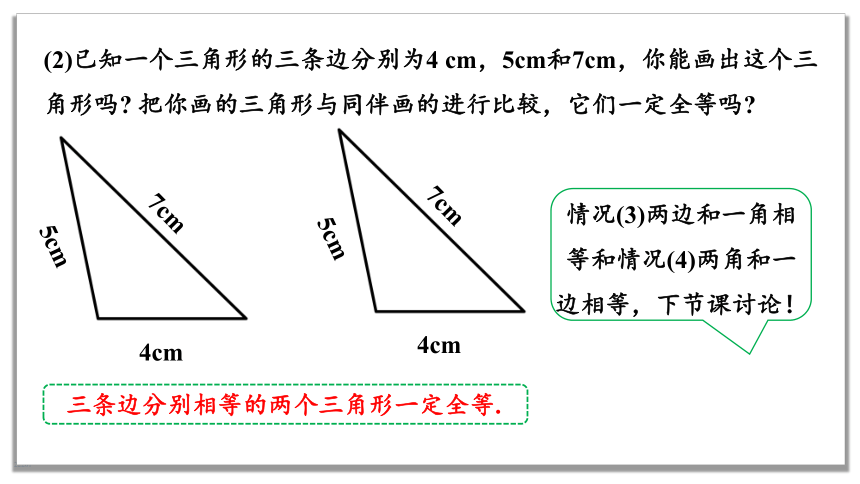
(2)已知一个三角形的三条边分别为4 cm,5cm和7cm,你能画出这个三角形吗 把你画的三角形与同伴画的进行比较,它们一定全等吗
4cm
5cm
7cm
4cm
5cm
7cm
三条边分别相等的两个三角形一定全等.
情况(3)两边和一角相等和情况(4)两角和一边相等,下节课讨论!
(3)小组合作,选择三条线段作为三角形的三条边,并用尺规作出这个三角形. 把你作的三角形与同伴作的进行比较,它们一定全等吗
如图,已知线段a,b,c,用尺规作△ABC,使AB=c,AC=b,BC=a.
a
b
c
②分别以点B,C为圆心,以c,b
的长为半径作弧,两弧交于点A.
作法与示范:
①作一条线段BC=a.
B
C
③连接AB,AC.
△ABC就是所要作的三角形.
B
C
A
B
C
A
归纳
数学语言:
A
B
C
D
E
F
在△ABC和△ DEF中,
所以 △ABC ≌△ DEF (SSS).
因为AB=DE,BC=EF,CA=FD,
三边分别相等的两个三角形全等,简写为“边边边”或“SSS”.
例 如图, C是BF的中点,AB =DC,AC=DF. 试说明: △ABC ≌△DCF.
解:因为C是BF中点,
所以BC=CF.
在△ABC 和△DCF中,
因为AB = DC,AC = DF,BC = CF,
所以 △ABC ≌ △DCF(SSS).
A
B
C
F
D
用小木条分别钉成一个三角形和四边形的框架,用力转动某一个
支点,框架的形状会发生改变吗?
探究
三角形的大小和形状是固定不变的,这个性质叫作三角形的稳定性;四边形的形状是可以改变的,四边形具有不稳定性.
思考
小明在钉成四边形框架的基础上,把对角又用一根木条钉起来了(如图),此时这个四边形是否具有稳定性?
此时的框架相当于两个三角形拼在一起,同样具有稳定性.
三角形的稳定性
(1)如果三角形的三边长确定,这个三角形的形状、大小就完全确定了,三角形的这种性质叫作三角形的稳定性.
(2)四边形及四边以上的图形,形状是可以改变的,因此具有不稳定性.
在生活中,我们经常会看到应用三角形稳定性的例子.
你还能举出其他例子吗?
晾衣架
自行车的车梁
塔吊
1. 如图,已知△ABC,则甲、乙、丙三个三角形中与△ABC全等的是
( B )
A. 甲 B. 乙 C. 丙 D. 甲和丙
B
2. 如图,AB=AD,BE=DE,BC=DC,则图中全等三角形有 ( B )
A. 2对 B. 3对 C. 4对 D. 5对
B
3.如图,AB=ED,C是BD边的中点,若添加一个条件,可用“SSS”判定
△ABC≌△EDC,这个条件是 ___________.
AC=EC
解:(1)因为AD=BE,
所以AD+DB=BE+DB,即AB=DE,
因为AC=DF,BC=EF,
所以△ABC≌△DEF;
4. 如图,点A、D、B、E在同一条直线上,AD=BE,AC=DF,BC=EF.
(1)试说明:△ABC≌△DEF;
A
D
C
B
E
F
(2)因为△ABC≌△DEF,∠A=55°,
所以∠A=∠FDE=55°,
因为∠E=45°,
所以∠F=180°-∠FDE-∠E=80°.
4. 如图,点A、D、B、E在同一条直线上,AD=BE,AC=DF,BC=EF
(2)若∠A=55°,∠E=45°,求∠F的度数.
A
D
C
B
E
F
5.如图,仪器ABCD可以用来平分一个角,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们落在角的两边上,沿AC画一条射线AE,AE就是∠PRQ的平分线. 你能说明其中的道理吗?
解:在△ABC和△ADC中,
因为AB=AD,BC=DC,AC=AC,
所以△ABC≌△ADC(SSS).
所以∠BAC=∠DAC,即∠QRE=∠PRE
故AE就是∠PRQ的平分线.
(全等三角形的对应角相等)
利用“边边边”
判定三角形全等
如果三角形的三边长确定,这个三角形的形状、大小就
完全确定了,三角形的这种性质叫作三角形的稳定性.
三边分别相等的两个三角形全等,简写为“边边边”或“SSS”.
第四章 三角形
4.3 课时1 利用“边边边”
判定三角形全等
1.理解并且会用“边边边”来判断三角形全等.
2.了解三角形的稳定性.
要画一个三角形,使它与小明画的三角形全等,你会怎么画呢
想一想,动手画一画吧!
要画一个与已知三角形全等的三角形,至少需要几个与边或角的大小有关的条件
我猜测至少需要三个与边或角的大小有关的条件.
(1)只有1个条件(1条边或1个角相等)时,可以吗?
1条边相等时,两个三角形不一定全等
1个角相等时,两个三角形不一定全等
(2)给出两个条件画三角形时,有哪几种可能的情况 每种情况下画出的三角形一定全等吗 请你试一试,并与同伴进行交流。
只给出一个条件或两个条件时,都不能保证所画出的三角形一定全等.
不一定全等
不一定全等
不一定全等
6cm
30°
3cm
4cm
3cm
4cm
30o
6cm
60o
30°
30°
60o
(1)有两个角分别相等的两个三角形
(2)有两条边分别相等的两个三角形
(3)有一个角和一条边分别相等的两个三角形
给出三个条件画三角形,有哪几种可能的情况?与同伴进行交流.
(1)三个角都相等;
(2)三条边都相等;
(3)两边和一角相等;
(4)两角和一边相等.
思考·交流
(1)已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗 把你画的三角形与同伴画的进行比较,它们一定全等吗
40°
60°
80°
40°
60°
80°
40°
60°
80°
40°
60°
80°
三个内角分别相等的两个三角形不一定全等.
尝试·思考
(2)已知一个三角形的三条边分别为4 cm,5cm和7cm,你能画出这个三角形吗 把你画的三角形与同伴画的进行比较,它们一定全等吗
4cm
5cm
7cm
4cm
5cm
7cm
三条边分别相等的两个三角形一定全等.
情况(3)两边和一角相等和情况(4)两角和一边相等,下节课讨论!
(3)小组合作,选择三条线段作为三角形的三条边,并用尺规作出这个三角形. 把你作的三角形与同伴作的进行比较,它们一定全等吗
如图,已知线段a,b,c,用尺规作△ABC,使AB=c,AC=b,BC=a.
a
b
c
②分别以点B,C为圆心,以c,b
的长为半径作弧,两弧交于点A.
作法与示范:
①作一条线段BC=a.
B
C
③连接AB,AC.
△ABC就是所要作的三角形.
B
C
A
B
C
A
归纳
数学语言:
A
B
C
D
E
F
在△ABC和△ DEF中,
所以 △ABC ≌△ DEF (SSS).
因为AB=DE,BC=EF,CA=FD,
三边分别相等的两个三角形全等,简写为“边边边”或“SSS”.
例 如图, C是BF的中点,AB =DC,AC=DF. 试说明: △ABC ≌△DCF.
解:因为C是BF中点,
所以BC=CF.
在△ABC 和△DCF中,
因为AB = DC,AC = DF,BC = CF,
所以 △ABC ≌ △DCF(SSS).
A
B
C
F
D
用小木条分别钉成一个三角形和四边形的框架,用力转动某一个
支点,框架的形状会发生改变吗?
探究
三角形的大小和形状是固定不变的,这个性质叫作三角形的稳定性;四边形的形状是可以改变的,四边形具有不稳定性.
思考
小明在钉成四边形框架的基础上,把对角又用一根木条钉起来了(如图),此时这个四边形是否具有稳定性?
此时的框架相当于两个三角形拼在一起,同样具有稳定性.
三角形的稳定性
(1)如果三角形的三边长确定,这个三角形的形状、大小就完全确定了,三角形的这种性质叫作三角形的稳定性.
(2)四边形及四边以上的图形,形状是可以改变的,因此具有不稳定性.
在生活中,我们经常会看到应用三角形稳定性的例子.
你还能举出其他例子吗?
晾衣架
自行车的车梁
塔吊
1. 如图,已知△ABC,则甲、乙、丙三个三角形中与△ABC全等的是
( B )
A. 甲 B. 乙 C. 丙 D. 甲和丙
B
2. 如图,AB=AD,BE=DE,BC=DC,则图中全等三角形有 ( B )
A. 2对 B. 3对 C. 4对 D. 5对
B
3.如图,AB=ED,C是BD边的中点,若添加一个条件,可用“SSS”判定
△ABC≌△EDC,这个条件是 ___________.
AC=EC
解:(1)因为AD=BE,
所以AD+DB=BE+DB,即AB=DE,
因为AC=DF,BC=EF,
所以△ABC≌△DEF;
4. 如图,点A、D、B、E在同一条直线上,AD=BE,AC=DF,BC=EF.
(1)试说明:△ABC≌△DEF;
A
D
C
B
E
F
(2)因为△ABC≌△DEF,∠A=55°,
所以∠A=∠FDE=55°,
因为∠E=45°,
所以∠F=180°-∠FDE-∠E=80°.
4. 如图,点A、D、B、E在同一条直线上,AD=BE,AC=DF,BC=EF
(2)若∠A=55°,∠E=45°,求∠F的度数.
A
D
C
B
E
F
5.如图,仪器ABCD可以用来平分一个角,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们落在角的两边上,沿AC画一条射线AE,AE就是∠PRQ的平分线. 你能说明其中的道理吗?
解:在△ABC和△ADC中,
因为AB=AD,BC=DC,AC=AC,
所以△ABC≌△ADC(SSS).
所以∠BAC=∠DAC,即∠QRE=∠PRE
故AE就是∠PRQ的平分线.
(全等三角形的对应角相等)
利用“边边边”
判定三角形全等
如果三角形的三边长确定,这个三角形的形状、大小就
完全确定了,三角形的这种性质叫作三角形的稳定性.
三边分别相等的两个三角形全等,简写为“边边边”或“SSS”.
同课章节目录
