4.3 课时2 利用“角边角、角角边”判定三角形全等 课件(共17张PPT) 2024-2025学年北师大版初中数学七年级下册
文档属性
| 名称 | 4.3 课时2 利用“角边角、角角边”判定三角形全等 课件(共17张PPT) 2024-2025学年北师大版初中数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
第四章 三角形
4.3 课时2 利用“角边角、角角边”
判定三角形全等
1.掌握三角形全等的“角边角”“角角边”判定方法.
2.会运用角边角定理尺规作三角形全等于已知三角形.
3.会用三角形全等的判定方法“角边角”“角角边”证明两个三角形全等.
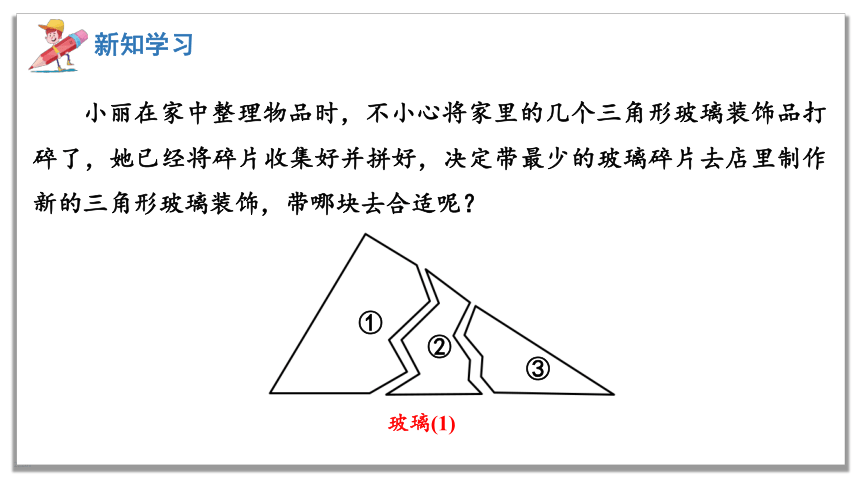
小丽在家中整理物品时,不小心将家里的几个三角形玻璃装饰品打碎了,她已经将碎片收集好并拼好,决定带最少的玻璃碎片去店里制作新的三角形玻璃装饰,带哪块去合适呢?
①
②
③
玻璃(1)
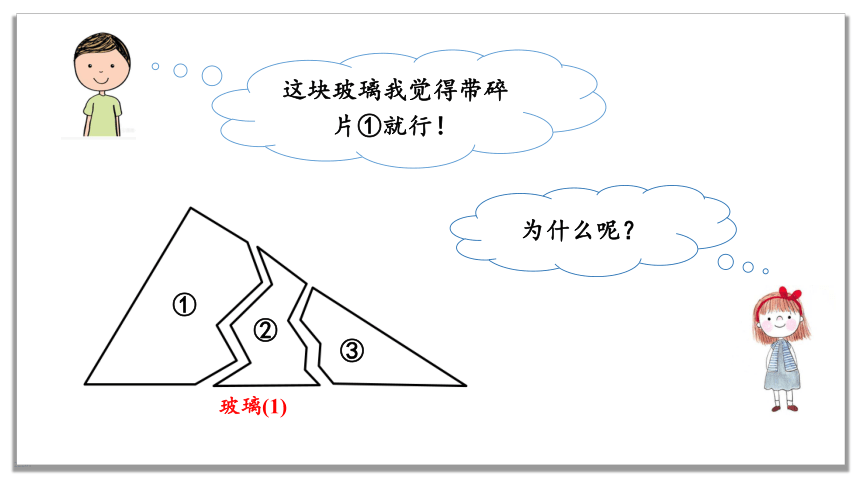
这块玻璃我觉得带碎片①就行!
为什么呢?
①
②
③
玻璃(1)
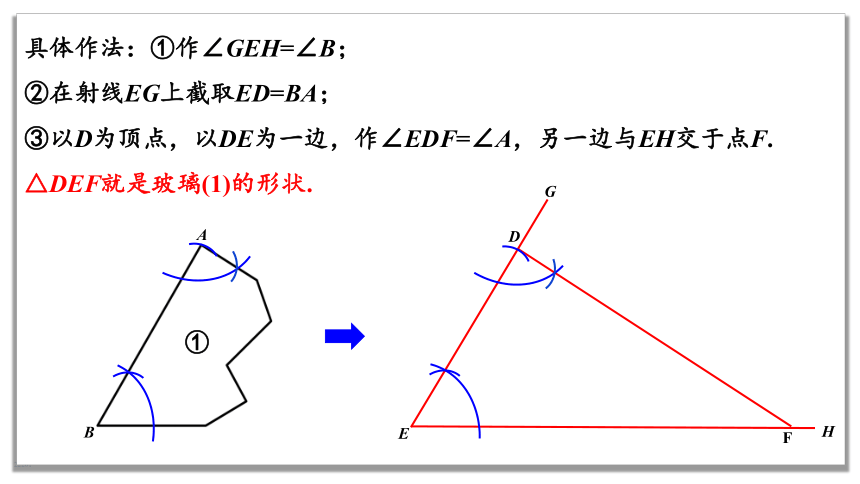
具体作法:①作∠GEH=∠B;
②在射线EG上截取ED=BA;
③以D为顶点,以DE为一边,作∠EDF=∠A,另一边与EH交于点F.
△DEF就是玻璃(1)的形状.
①
A
B
E
F
D
G
H
用“角边角”判定三角形全等:
两角及其夹边分别相等的两个三角形全等,简写为“角边角”或“ASA”.
数学语言:如图,在△ABC和△DEF中,
因为∠B=∠E,BC=EF,∠C=∠F,
所以△ABC≌△DEF(ASA).
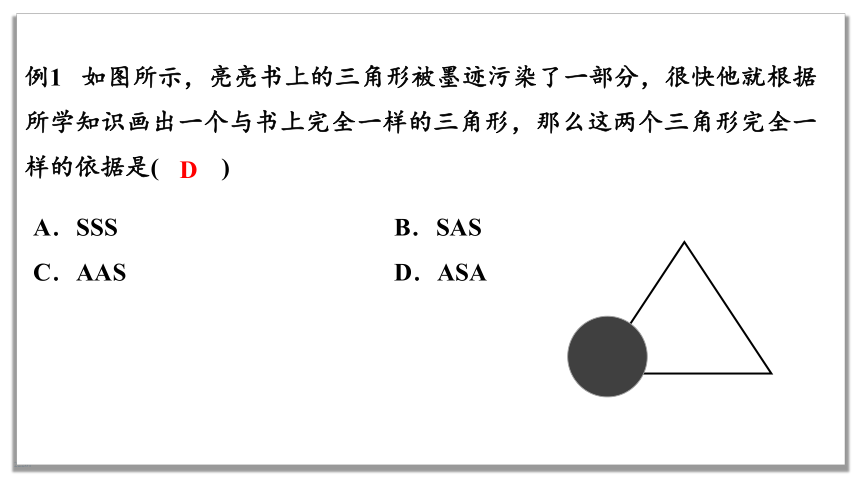
例1 如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.SSS B.SAS
C.AAS D.ASA
D
玻璃(2)我带碎片①和碎片③就可以还原整块玻璃.
①
②
③
玻璃(2)
①
③
A
B
C
E
F
G
D
H
具体作法:①作∠GEH=∠B;
②在射线EH上截取EF=BC;
③根据三角形内角和定理,计算出∠BCA的度数,并以F为顶点,以EF为一边,作∠EFD=∠BCA,另一边与EG交于点D.
④量得∠EDF=∠A.
△DEF就是玻璃(2)的形状.
用“角角边”判定三角形全等:
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写为“角角边”或“AAS”.
数学语言:如图,在△ABC和△DEF中,因为∠B=∠E,∠C=∠F,AC=DF,
所以△ABC≌△DEF (AAS).
例2 如图,已知∠1=∠2,若用“AAS”说明△ACB≌△BDA,还需添加条件( )
A.AD=BC B.BD=AC
C.∠D=∠C D.OA=OB
C
1
2
A
D
C
B
O
1. 在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°,∠A′=44°,且AC=A′C′,那么这两个三角形( )
B
A.一定不全等 B.一定全等
C.不一定全等 D.以上都不对
2. 如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判断下面的两个三角形是否全等,并说明理由.
解:不全等,因为BC虽然是公共边,但不是对应边.
A
B
C
D
3. 图中的两个三角形全等吗?请说明理由.
110°
110°
35°
35°
解:两个三角形全等;根据图中信息,三角形已经有两个角相等,且有一条边为公共边且为对应边,符合“角角边”的判定定理.
4. 已知:如图,点B,F,C,D在一条直线上,AB=ED, AB∥ED,AC∥EF. △ABC和△EDF全等吗,请说明理由.
解:△ABC和△EDF全等,理由如下:
因为 AB∥ED,AC∥EF,
所以∠B=∠D,∠ACB=∠EFD.
在△ABC与△EDF中,
因为∠B=∠D,∠ACB=∠EFD,AB=ED,
根据三角形全等的判定条件“AAS”,
可以得到△ ABC ≌△ EDF .
5. 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C ,
试说明:AD=AE.
A
B
C
D
E
解:在△ACD和△ABE中,
因为∠A=∠A , AC=AB ,∠C=∠B,
可以得到△ACD≌△ABE.
所以AD=AE.
根据三角形全等的判定条件“ASA”,
利用“角边角、
角角边”
判定三角形全等
用“ASA”判定
三角形全等
用“AAS”判定
三角形全等
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”.
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
数学语言:如图,在△ABC和△DEF中,因为∠B=∠E,BC=EF,∠C=∠F,
所以△ABC≌△DEF(ASA).
数学语言:如图,在△ABC和△DEF中,因为∠B=∠E,∠C=∠F,AC=DF,
所以△ABC≌△DEF(AAS).
第四章 三角形
4.3 课时2 利用“角边角、角角边”
判定三角形全等
1.掌握三角形全等的“角边角”“角角边”判定方法.
2.会运用角边角定理尺规作三角形全等于已知三角形.
3.会用三角形全等的判定方法“角边角”“角角边”证明两个三角形全等.
小丽在家中整理物品时,不小心将家里的几个三角形玻璃装饰品打碎了,她已经将碎片收集好并拼好,决定带最少的玻璃碎片去店里制作新的三角形玻璃装饰,带哪块去合适呢?
①
②
③
玻璃(1)
这块玻璃我觉得带碎片①就行!
为什么呢?
①
②
③
玻璃(1)
具体作法:①作∠GEH=∠B;
②在射线EG上截取ED=BA;
③以D为顶点,以DE为一边,作∠EDF=∠A,另一边与EH交于点F.
△DEF就是玻璃(1)的形状.
①
A
B
E
F
D
G
H
用“角边角”判定三角形全等:
两角及其夹边分别相等的两个三角形全等,简写为“角边角”或“ASA”.
数学语言:如图,在△ABC和△DEF中,
因为∠B=∠E,BC=EF,∠C=∠F,
所以△ABC≌△DEF(ASA).
例1 如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.SSS B.SAS
C.AAS D.ASA
D
玻璃(2)我带碎片①和碎片③就可以还原整块玻璃.
①
②
③
玻璃(2)
①
③
A
B
C
E
F
G
D
H
具体作法:①作∠GEH=∠B;
②在射线EH上截取EF=BC;
③根据三角形内角和定理,计算出∠BCA的度数,并以F为顶点,以EF为一边,作∠EFD=∠BCA,另一边与EG交于点D.
④量得∠EDF=∠A.
△DEF就是玻璃(2)的形状.
用“角角边”判定三角形全等:
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写为“角角边”或“AAS”.
数学语言:如图,在△ABC和△DEF中,因为∠B=∠E,∠C=∠F,AC=DF,
所以△ABC≌△DEF (AAS).
例2 如图,已知∠1=∠2,若用“AAS”说明△ACB≌△BDA,还需添加条件( )
A.AD=BC B.BD=AC
C.∠D=∠C D.OA=OB
C
1
2
A
D
C
B
O
1. 在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°,∠A′=44°,且AC=A′C′,那么这两个三角形( )
B
A.一定不全等 B.一定全等
C.不一定全等 D.以上都不对
2. 如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判断下面的两个三角形是否全等,并说明理由.
解:不全等,因为BC虽然是公共边,但不是对应边.
A
B
C
D
3. 图中的两个三角形全等吗?请说明理由.
110°
110°
35°
35°
解:两个三角形全等;根据图中信息,三角形已经有两个角相等,且有一条边为公共边且为对应边,符合“角角边”的判定定理.
4. 已知:如图,点B,F,C,D在一条直线上,AB=ED, AB∥ED,AC∥EF. △ABC和△EDF全等吗,请说明理由.
解:△ABC和△EDF全等,理由如下:
因为 AB∥ED,AC∥EF,
所以∠B=∠D,∠ACB=∠EFD.
在△ABC与△EDF中,
因为∠B=∠D,∠ACB=∠EFD,AB=ED,
根据三角形全等的判定条件“AAS”,
可以得到△ ABC ≌△ EDF .
5. 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C ,
试说明:AD=AE.
A
B
C
D
E
解:在△ACD和△ABE中,
因为∠A=∠A , AC=AB ,∠C=∠B,
可以得到△ACD≌△ABE.
所以AD=AE.
根据三角形全等的判定条件“ASA”,
利用“角边角、
角角边”
判定三角形全等
用“ASA”判定
三角形全等
用“AAS”判定
三角形全等
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”.
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
数学语言:如图,在△ABC和△DEF中,因为∠B=∠E,BC=EF,∠C=∠F,
所以△ABC≌△DEF(ASA).
数学语言:如图,在△ABC和△DEF中,因为∠B=∠E,∠C=∠F,AC=DF,
所以△ABC≌△DEF(AAS).
同课章节目录
