4.3 课时3 利用“边角边”判定三角形全等 课件(共17张PPT) 2024-2025学年北师大版初中数学七年级下册
文档属性
| 名称 | 4.3 课时3 利用“边角边”判定三角形全等 课件(共17张PPT) 2024-2025学年北师大版初中数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 15.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 19:49:34 | ||
图片预览



文档简介
(共17张PPT)
第四章 三角形
4.3 课时3 利用“边角边”
判定三角形全等
1.掌握三角形全等的“边角边”判定方法.
2.会运用“边角边”定理尺规作三角形全等于已知三角形.
3.会运用“边角边”判定方法进行简单的说理.
4.知道已知两边一角不一定能判断两个三角形全等.
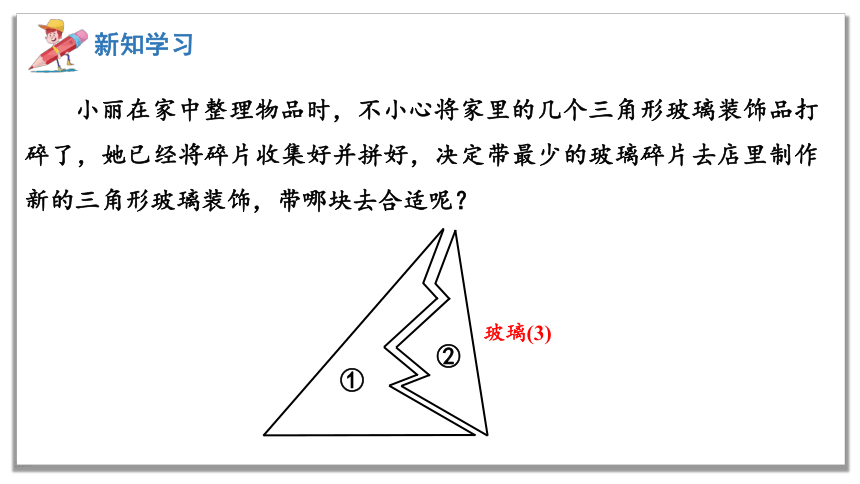
小丽在家中整理物品时,不小心将家里的几个三角形玻璃装饰品打碎了,她已经将碎片收集好并拼好,决定带最少的玻璃碎片去店里制作新的三角形玻璃装饰,带哪块去合适呢?
①
②
玻璃(3)
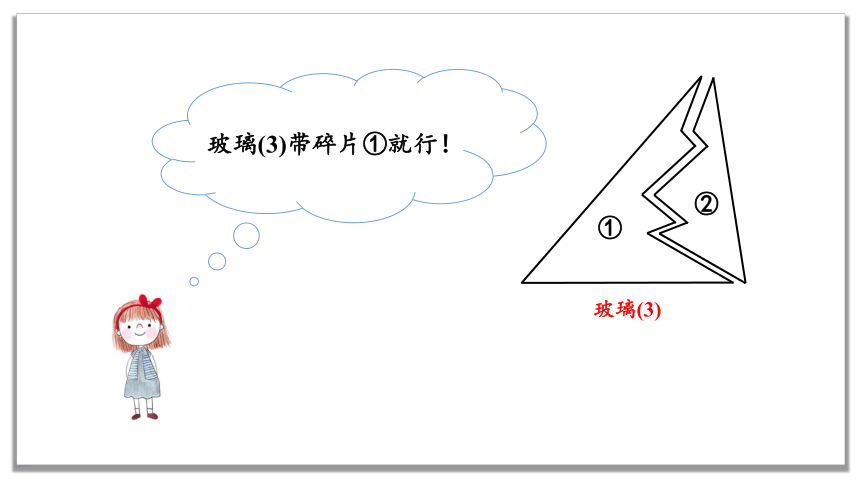
①
②
玻璃(3)
玻璃(3)带碎片①就行!
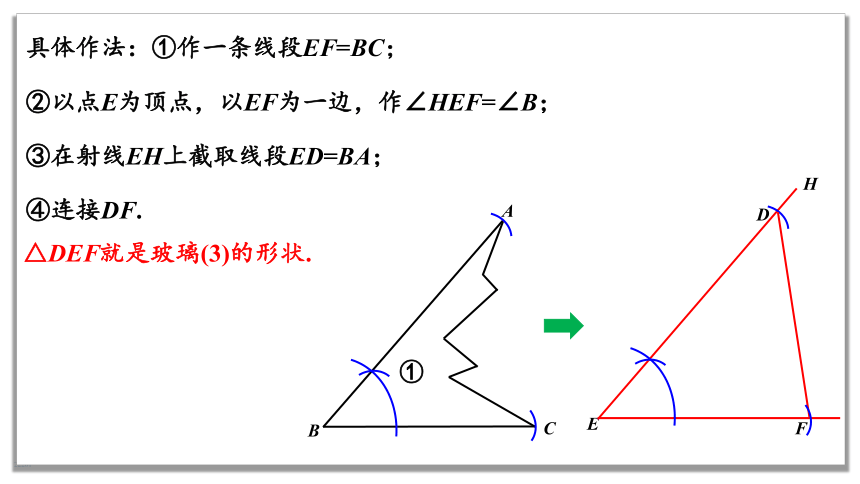
具体作法:①作一条线段EF=BC;
②以点E为顶点,以EF为一边,作∠HEF=∠B;
③在射线EH上截取线段ED=BA;
④连接DF.
①
E
F
H
D
B
C
A
△DEF就是玻璃(3)的形状.
用“边角边”判定三角形全等:
两边及其夹角分别相等的两个三角形全等,简写为“边角边”或“SAS”.
数学语言:如图,在△ABC和△DEF中,因为AB=DE,∠B=∠E,BC=EF,
所以△ABC≌△DEF (SAS).
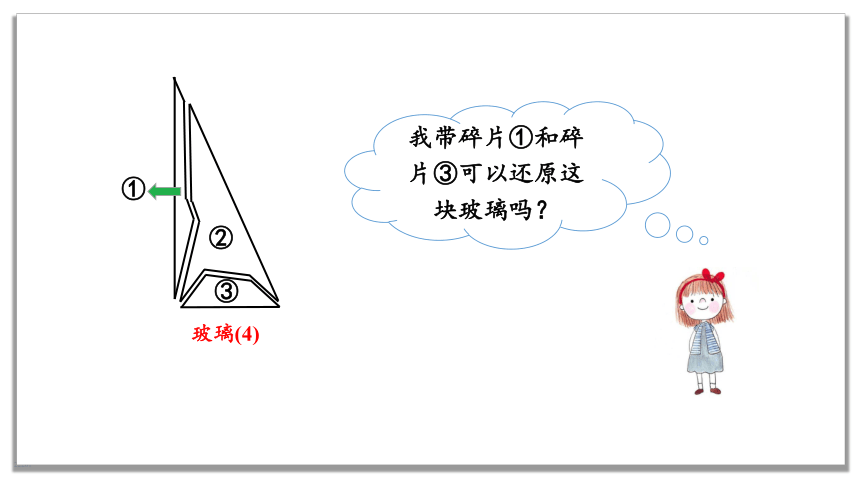
玻璃(4)
①
②
③
我带碎片①和碎片③可以还原这块玻璃吗?
具体作法:①作一条线段ED=BA;
②以点D为顶点,以DE为一边,作∠EDH=∠A;
③画直线EF=BC.
①
③
B
C
A
E
D
H
哪条线才是真正的EF?
两边分别相等且其中一组等边的对角相等的两个三角形不一定全等.
例1 如果AB=CB,BD是∠ABC的平分线,那么△ABD 和△CBD全等吗?
A
B
C
D
解:由题意可得BD是∠ABC的平分线,
所以∠ABD=∠CBD.
△ABD与△CBD中
因为 AB=CB,∠ABD=∠CBD,BD=BD.
根据三角形全等的判定条件“SAS”
可以得到△ABD≌△CBD .
已知: AD=CD,DB平分∠ADC ,试说明:∠A=∠C.
A
B
C
D
1
2
变式
解:由题意可得DB 平分∠ADC,
所以∠1=∠2.
在△ABD与△CBD中,
因为AD=CD,∠1=∠2,BD=BD,
根据三角形全等的判定条件“SAS”
可以得到△ABD≌△CBD,
所以∠A=∠C.
1. 如图,AD为∠BAC的平分线,若要用“SAS”判定△ABD≌△ACD,则
还需要添加的条件是 ( C )
A. ∠B=∠C B. BD=CD
C. AB=AC D. ∠ADB=∠ADC
C
2. 如图,将两根钢条AB,CD的中点O钉在一起,使AB,CD可以绕点O自由转动,就做成了一个测量工件,可得B,D之间的距离等于内槽宽AC,则判定△OAC≌△OBD的依据是( C )
A. SSS B. ASA C. SAS D. AAS
C
A.∠A=∠D B.∠AFB=∠DEC
C. AB=CD D. AF=DE
3.如图,点E、点F在BC上,BE=CF,∠B=∠C,添加一个条件,不能说明△ABF≌△DCE的是( )
D
A
D
C
B
E
F
4.分别找出各题中的全等三角形,并说明理由.
A
B
C
D
E
F
A
B
C
D
40°
40°
(1)
(2)
解:△ABC≌△EFD(SAS)
△ABC≌△CDA(SAS)
5.小明做了一个如图所示的风筝,其中∠EDH=∠FDH,ED=FD. 将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同伴进行交流.
解:在△DEH与△DFH中
因为ED=FD,∠EDH=∠FDH,DH=DH
根据三角形全等的判定条件“SAS”
可以得到△DEH≌△DFH.
所以EH=FH .
6. 如图,在△ABC和△AED中,AB=AE,∠BAE=∠CAD,AC=AD. △ABC和△AED全等吗?
A
D
C
B
E
解:△ABC和△AED全等,理由如下:
因为∠BAE=∠CAD,
所以∠BAE+∠CAE=∠CAD+∠CAE,即∠BAC=∠EAD.
在△ABC与△AED中,
因为AB=AE,∠BAC=∠EAD,AC=AD,
根据三角形全等的判定条件“SAS”
可以得到△ABC≌△AED.
利用“边角边”
判定三角形全等
两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.
数学语言:如图,在△ABC和△DEF中,因为AB=DE,∠B=∠E,BC=EF,
所以△ABC≌△DEF(SAS).
第四章 三角形
4.3 课时3 利用“边角边”
判定三角形全等
1.掌握三角形全等的“边角边”判定方法.
2.会运用“边角边”定理尺规作三角形全等于已知三角形.
3.会运用“边角边”判定方法进行简单的说理.
4.知道已知两边一角不一定能判断两个三角形全等.
小丽在家中整理物品时,不小心将家里的几个三角形玻璃装饰品打碎了,她已经将碎片收集好并拼好,决定带最少的玻璃碎片去店里制作新的三角形玻璃装饰,带哪块去合适呢?
①
②
玻璃(3)
①
②
玻璃(3)
玻璃(3)带碎片①就行!
具体作法:①作一条线段EF=BC;
②以点E为顶点,以EF为一边,作∠HEF=∠B;
③在射线EH上截取线段ED=BA;
④连接DF.
①
E
F
H
D
B
C
A
△DEF就是玻璃(3)的形状.
用“边角边”判定三角形全等:
两边及其夹角分别相等的两个三角形全等,简写为“边角边”或“SAS”.
数学语言:如图,在△ABC和△DEF中,因为AB=DE,∠B=∠E,BC=EF,
所以△ABC≌△DEF (SAS).
玻璃(4)
①
②
③
我带碎片①和碎片③可以还原这块玻璃吗?
具体作法:①作一条线段ED=BA;
②以点D为顶点,以DE为一边,作∠EDH=∠A;
③画直线EF=BC.
①
③
B
C
A
E
D
H
哪条线才是真正的EF?
两边分别相等且其中一组等边的对角相等的两个三角形不一定全等.
例1 如果AB=CB,BD是∠ABC的平分线,那么△ABD 和△CBD全等吗?
A
B
C
D
解:由题意可得BD是∠ABC的平分线,
所以∠ABD=∠CBD.
△ABD与△CBD中
因为 AB=CB,∠ABD=∠CBD,BD=BD.
根据三角形全等的判定条件“SAS”
可以得到△ABD≌△CBD .
已知: AD=CD,DB平分∠ADC ,试说明:∠A=∠C.
A
B
C
D
1
2
变式
解:由题意可得DB 平分∠ADC,
所以∠1=∠2.
在△ABD与△CBD中,
因为AD=CD,∠1=∠2,BD=BD,
根据三角形全等的判定条件“SAS”
可以得到△ABD≌△CBD,
所以∠A=∠C.
1. 如图,AD为∠BAC的平分线,若要用“SAS”判定△ABD≌△ACD,则
还需要添加的条件是 ( C )
A. ∠B=∠C B. BD=CD
C. AB=AC D. ∠ADB=∠ADC
C
2. 如图,将两根钢条AB,CD的中点O钉在一起,使AB,CD可以绕点O自由转动,就做成了一个测量工件,可得B,D之间的距离等于内槽宽AC,则判定△OAC≌△OBD的依据是( C )
A. SSS B. ASA C. SAS D. AAS
C
A.∠A=∠D B.∠AFB=∠DEC
C. AB=CD D. AF=DE
3.如图,点E、点F在BC上,BE=CF,∠B=∠C,添加一个条件,不能说明△ABF≌△DCE的是( )
D
A
D
C
B
E
F
4.分别找出各题中的全等三角形,并说明理由.
A
B
C
D
E
F
A
B
C
D
40°
40°
(1)
(2)
解:△ABC≌△EFD(SAS)
△ABC≌△CDA(SAS)
5.小明做了一个如图所示的风筝,其中∠EDH=∠FDH,ED=FD. 将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同伴进行交流.
解:在△DEH与△DFH中
因为ED=FD,∠EDH=∠FDH,DH=DH
根据三角形全等的判定条件“SAS”
可以得到△DEH≌△DFH.
所以EH=FH .
6. 如图,在△ABC和△AED中,AB=AE,∠BAE=∠CAD,AC=AD. △ABC和△AED全等吗?
A
D
C
B
E
解:△ABC和△AED全等,理由如下:
因为∠BAE=∠CAD,
所以∠BAE+∠CAE=∠CAD+∠CAE,即∠BAC=∠EAD.
在△ABC与△AED中,
因为AB=AE,∠BAC=∠EAD,AC=AD,
根据三角形全等的判定条件“SAS”
可以得到△ABC≌△AED.
利用“边角边”
判定三角形全等
两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.
数学语言:如图,在△ABC和△DEF中,因为AB=DE,∠B=∠E,BC=EF,
所以△ABC≌△DEF(SAS).
同课章节目录
