4.3 课时4 三角形全等的综合运用 课件(共17张PPT) 2024-2025学年北师大版初中数学七年级下册
文档属性
| 名称 | 4.3 课时4 三角形全等的综合运用 课件(共17张PPT) 2024-2025学年北师大版初中数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 14.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
4.3 课时4 三角形全等的综合运用
第四章 三角形
1. 熟练掌握三角形全等的 4 种判定方法.
2. 能灵活地运用这四种方法来判定两个三角形全等.
判定三角形全等的方法有哪些?
(1) 三边分别相等的两个三角形全等;
(2) 两角及其夹边分别相等的两个三角形全等;
(3) 两角分别相等且其中一组等角的对边相等的两个三角形全等;
(4) 两边及其夹角分别相等的两个三角形全等.
回顾
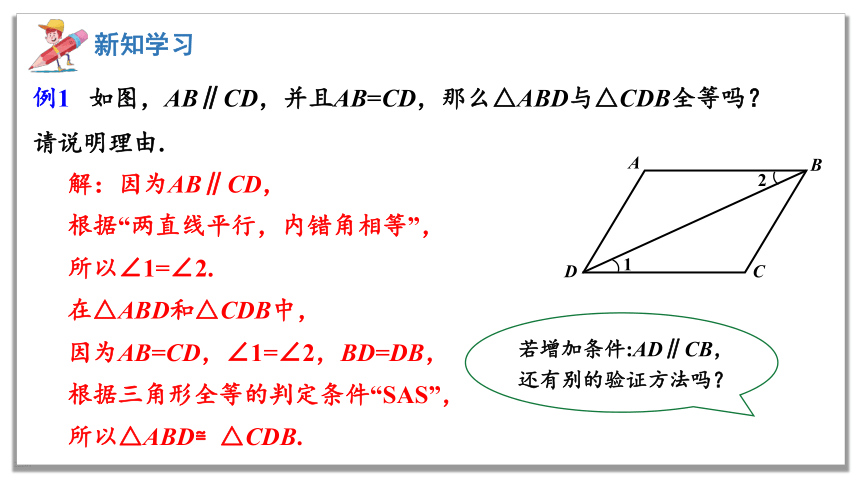
例1 如图,AB∥CD,并且AB=CD,那么△ABD与△CDB全等吗?请说明理由.
解:因为AB∥CD,
根据“两直线平行,内错角相等”,
所以∠1=∠2.
在△ABD和△CDB中,
因为AB=CD,∠1=∠2,BD=DB,
根据三角形全等的判定条件“SAS”,
所以△ABD≌△CDB.
1
2
A
D
C
B
若增加条件:AD∥CB,还有别的验证方法吗?
如图,AD∥CB,AB∥CD,并且AB=CD,那么△ABD与△CDB全等吗?
方法一:因为AD∥CB,AB∥CD,
根据“两直线平行,内错角相等”,
所以∠1=∠2,∠3=∠4.
在△ABD和△CDB中,
因为AB=CD,∠1=∠2,∠3=∠4,
根据三角形全等的判定条件“AAS”,
所以△ABD≌△CDB
变式
1
2
A
D
C
B
3
4
如图,AD∥CB,AB∥CD,并且AB=CD,那么△ABD与△CDB全等吗?
方法二:因为AD∥CB,AB∥CD,
根据“两直线平行,内错角相等”,
所以∠1=∠2,∠3=∠4.
在△ABD和△CDB中,
因为BD=DB,∠1=∠2,∠3=∠4,
根据三角形全等的判定条件“ASA”,
所以△ABD≌△CDB
变式
1
2
A
D
C
B
3
4
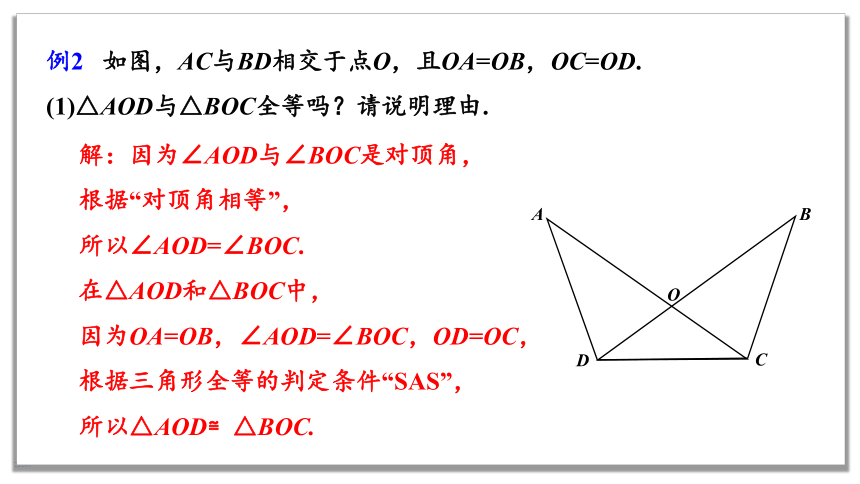
解:因为∠AOD与∠BOC是对顶角,
根据“对顶角相等”,
所以∠AOD=∠BOC.
在△AOD和△BOC中,
因为OA=OB,∠AOD=∠BOC,OD=OC,
根据三角形全等的判定条件“SAS”,
所以△AOD≌△BOC.
例2 如图,AC与BD相交于点O,且OA=OB,OC=OD.
(1)△AOD与△BOC全等吗?请说明理由.
A
D
C
B
O
A
D
C
B
O
例2 如图,AC与BD相交于点O,且OA=OB,OC=OD.
(2)△ACD与△BDC全等吗?为什么?
解:由(1)可知,△AOD≌△BOC,
根据“全等三角形的对应边相等”,所以AD=BC.
因为OA=OB,OC=OD,AC=OA+OC,BD=OB+OD. 所以AC=BD.
在△ACD和△BDC中,
因为AD=BC,AC=BD,DC=CD,
根据三角形全等的判定条件“SSS”,
所以△ACD≌△BDC.
你还能根据其他的判定条件,判断这两个三角形全等吗?
例2 如图,AC与BD相交于点O,且OA=OB,OC=OD.
(2)△ACD与△BDC全等吗?为什么?
A
D
C
B
O
方法二:由(1)可知,△AOD≌△BOC,
根据“全等三角形的对应边相等,对应角相等”,所以AD=BC,∠A=∠B.
因为OA=OB,OC=OD,AC=OA+OC,BD=OB+OD. 所以AC=BD.
在△ACD和△BDC中,
因为AD=BC,AC=BD,∠A=∠B,
根据三角形全等的判定条件“SAS”,
所以△ACD≌△BDC.
已知条件 寻找的条件 选择的判定方法
两角
一角及其对边
一角及其邻边
两边
任一边
任一角
角的另一邻边或任一角
夹角或另一边
ASA或AAS
AAS
SAS或ASA或AAS
SAS或SSS
归纳
1. 如图,在△ABC中,D,E为BC边上两点,AB=AC,添加下列条件
不.能.判定△ABE≌△ACD的是( B )
A. ∠B=∠C,BE=CD
B. BE=AD,∠BAE=∠CAD
C. ∠ADC=∠AEB,∠B=∠C
D. ∠B=∠C,∠BAE=∠CAD
B
2. 如图,△ABC中,D是AB上一点,CF∥AB,D、E、F三点共线,请添加一个条件 ,使得AE=CE.(只添一种情况即可)
B
C
D
E
A
F
DE=EF
3. 如图 AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△CEB全等吗?
为什么?
解:全等,理由如下:
因为AE=CF,
所以AE-FE=CF-EF,即 AF=CE.
在△AFD和△CEB中,
AF=CE,∠AFD=∠CEB,DF=BE.
根据三角形全等的判定条件“SAS”,
所以△AFD≌△CEB.
A
D
B
C
F
E
4. 如图,点C在线段AD上,AB=AD,∠B=∠D,BC=DE.
试说明: △ABC≌△ADE;
解:在△ABC和△ADE中,
BC=DE,∠B=∠D,AB=AD,
根据三角形全等的判定条件“SAS”,
所以△ABC≌△ADE.
A
D
C
B
E
解:因为点D为BC边的中点,所以BD=CD,
因为BE∥AC,所以∠EBD=∠C,∠E=∠CAD,
在△BDE和△CDA中,
∠EBD=∠C,∠E=∠CAD,BD=CD.
根据三角形全等的判定条件“AAS”
所以△BDE≌△CDA.
5. 如图,在△ABC中,点D为BC边的中点,过点B作BE∥AC交AD的延长线于点E.
(1)试说明:△BDE≌△CDA.
A
D
C
B
E
5. 如图,在△ABC中,点D为BC边的中点,过点B作BE∥AC交AD的延长线于点E.
(2)若AD⊥BC,试说明:BA=BE.
解:因为点D为BC边的中点,所以BD=CD
又因为AD⊥BC,所以∠ADB=∠ADC
在△ABD和△ACD中,
AD=AD,∠ADB=∠ADC,BD=CD.
根据三角形全等的判定条件“SAS”
所以△ABD≌△ACD.
A
D
C
B
E
所以BA=CA
由(1)得△BDE≌△CDA,
所以BE=CA,
所以BA=BE.
已知条件 寻找的条件 选择的判定方法
两角
一角及其对边
一角及其邻边
两边
任一边
任一角
角的另一邻边或任一角
夹角或另一边
ASA或AAS
AAS
SAS或ASA或AAS
SAS或SSS
4.3 课时4 三角形全等的综合运用
第四章 三角形
1. 熟练掌握三角形全等的 4 种判定方法.
2. 能灵活地运用这四种方法来判定两个三角形全等.
判定三角形全等的方法有哪些?
(1) 三边分别相等的两个三角形全等;
(2) 两角及其夹边分别相等的两个三角形全等;
(3) 两角分别相等且其中一组等角的对边相等的两个三角形全等;
(4) 两边及其夹角分别相等的两个三角形全等.
回顾
例1 如图,AB∥CD,并且AB=CD,那么△ABD与△CDB全等吗?请说明理由.
解:因为AB∥CD,
根据“两直线平行,内错角相等”,
所以∠1=∠2.
在△ABD和△CDB中,
因为AB=CD,∠1=∠2,BD=DB,
根据三角形全等的判定条件“SAS”,
所以△ABD≌△CDB.
1
2
A
D
C
B
若增加条件:AD∥CB,还有别的验证方法吗?
如图,AD∥CB,AB∥CD,并且AB=CD,那么△ABD与△CDB全等吗?
方法一:因为AD∥CB,AB∥CD,
根据“两直线平行,内错角相等”,
所以∠1=∠2,∠3=∠4.
在△ABD和△CDB中,
因为AB=CD,∠1=∠2,∠3=∠4,
根据三角形全等的判定条件“AAS”,
所以△ABD≌△CDB
变式
1
2
A
D
C
B
3
4
如图,AD∥CB,AB∥CD,并且AB=CD,那么△ABD与△CDB全等吗?
方法二:因为AD∥CB,AB∥CD,
根据“两直线平行,内错角相等”,
所以∠1=∠2,∠3=∠4.
在△ABD和△CDB中,
因为BD=DB,∠1=∠2,∠3=∠4,
根据三角形全等的判定条件“ASA”,
所以△ABD≌△CDB
变式
1
2
A
D
C
B
3
4
解:因为∠AOD与∠BOC是对顶角,
根据“对顶角相等”,
所以∠AOD=∠BOC.
在△AOD和△BOC中,
因为OA=OB,∠AOD=∠BOC,OD=OC,
根据三角形全等的判定条件“SAS”,
所以△AOD≌△BOC.
例2 如图,AC与BD相交于点O,且OA=OB,OC=OD.
(1)△AOD与△BOC全等吗?请说明理由.
A
D
C
B
O
A
D
C
B
O
例2 如图,AC与BD相交于点O,且OA=OB,OC=OD.
(2)△ACD与△BDC全等吗?为什么?
解:由(1)可知,△AOD≌△BOC,
根据“全等三角形的对应边相等”,所以AD=BC.
因为OA=OB,OC=OD,AC=OA+OC,BD=OB+OD. 所以AC=BD.
在△ACD和△BDC中,
因为AD=BC,AC=BD,DC=CD,
根据三角形全等的判定条件“SSS”,
所以△ACD≌△BDC.
你还能根据其他的判定条件,判断这两个三角形全等吗?
例2 如图,AC与BD相交于点O,且OA=OB,OC=OD.
(2)△ACD与△BDC全等吗?为什么?
A
D
C
B
O
方法二:由(1)可知,△AOD≌△BOC,
根据“全等三角形的对应边相等,对应角相等”,所以AD=BC,∠A=∠B.
因为OA=OB,OC=OD,AC=OA+OC,BD=OB+OD. 所以AC=BD.
在△ACD和△BDC中,
因为AD=BC,AC=BD,∠A=∠B,
根据三角形全等的判定条件“SAS”,
所以△ACD≌△BDC.
已知条件 寻找的条件 选择的判定方法
两角
一角及其对边
一角及其邻边
两边
任一边
任一角
角的另一邻边或任一角
夹角或另一边
ASA或AAS
AAS
SAS或ASA或AAS
SAS或SSS
归纳
1. 如图,在△ABC中,D,E为BC边上两点,AB=AC,添加下列条件
不.能.判定△ABE≌△ACD的是( B )
A. ∠B=∠C,BE=CD
B. BE=AD,∠BAE=∠CAD
C. ∠ADC=∠AEB,∠B=∠C
D. ∠B=∠C,∠BAE=∠CAD
B
2. 如图,△ABC中,D是AB上一点,CF∥AB,D、E、F三点共线,请添加一个条件 ,使得AE=CE.(只添一种情况即可)
B
C
D
E
A
F
DE=EF
3. 如图 AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△CEB全等吗?
为什么?
解:全等,理由如下:
因为AE=CF,
所以AE-FE=CF-EF,即 AF=CE.
在△AFD和△CEB中,
AF=CE,∠AFD=∠CEB,DF=BE.
根据三角形全等的判定条件“SAS”,
所以△AFD≌△CEB.
A
D
B
C
F
E
4. 如图,点C在线段AD上,AB=AD,∠B=∠D,BC=DE.
试说明: △ABC≌△ADE;
解:在△ABC和△ADE中,
BC=DE,∠B=∠D,AB=AD,
根据三角形全等的判定条件“SAS”,
所以△ABC≌△ADE.
A
D
C
B
E
解:因为点D为BC边的中点,所以BD=CD,
因为BE∥AC,所以∠EBD=∠C,∠E=∠CAD,
在△BDE和△CDA中,
∠EBD=∠C,∠E=∠CAD,BD=CD.
根据三角形全等的判定条件“AAS”
所以△BDE≌△CDA.
5. 如图,在△ABC中,点D为BC边的中点,过点B作BE∥AC交AD的延长线于点E.
(1)试说明:△BDE≌△CDA.
A
D
C
B
E
5. 如图,在△ABC中,点D为BC边的中点,过点B作BE∥AC交AD的延长线于点E.
(2)若AD⊥BC,试说明:BA=BE.
解:因为点D为BC边的中点,所以BD=CD
又因为AD⊥BC,所以∠ADB=∠ADC
在△ABD和△ACD中,
AD=AD,∠ADB=∠ADC,BD=CD.
根据三角形全等的判定条件“SAS”
所以△ABD≌△ACD.
A
D
C
B
E
所以BA=CA
由(1)得△BDE≌△CDA,
所以BE=CA,
所以BA=BE.
已知条件 寻找的条件 选择的判定方法
两角
一角及其对边
一角及其邻边
两边
任一边
任一角
角的另一邻边或任一角
夹角或另一边
ASA或AAS
AAS
SAS或ASA或AAS
SAS或SSS
同课章节目录
