第三单元圆柱与圆锥(知识梳理+拔高训练)二(含解析)-2024-2025学年六年级数学下学期尖子生培优检测卷(人教版)
文档属性
| 名称 | 第三单元圆柱与圆锥(知识梳理+拔高训练)二(含解析)-2024-2025学年六年级数学下学期尖子生培优检测卷(人教版) |  | |
| 格式 | docx | ||
| 文件大小 | 338.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-07 20:13:50 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第三单元圆柱与圆锥(知识梳理+拔高训练)二
知识梳理
知识点01:圆柱
1、圆柱的形成:圆柱是以长方形的一边为轴旋转而得到的。
圆柱也可以由长方形卷曲而得到。(两种方式:①以长方形的长为底面周长,宽为高;②以长方形的宽为底面周长,长为高。其中,第一种方式得到的圆柱体体积较大。)
2、圆柱的高是两个底面之间的距离,一个圆柱有无数条高,他们的数值是相等的。
3、圆柱的特征:
(1)底面的特征:圆柱的底面是完全相等的两个圆。
(2)侧面的特征:圆柱的侧面是一个曲面。
(3)高的特征 :圆柱有无数条高。
4、圆柱的切割:①横切:切面是圆,表面积增加 2 倍底面积,即 S增 =2πr ;
②竖切(过直径):切面是长方形(如果 h=2R,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4rh。
5、圆柱的侧面展开图:①沿着高展开,展开图形是长方形,如果 h=2πr,展开图形为正方形;
②不沿着高展开,展开图形是平行四边形或不规则图形;
③无论怎么展开都得不到梯形。
6、圆柱的相关计算公式:底面积 :S底=πr
底面周长:C底=πd=2πr
侧面积:S侧=2πrh
表面积:S表=2S底+S侧=2πr +2πrh
体积:V柱=πr h
知识点02:圆锥
1、圆柱的形成:圆锥是以直角三角形的一直角边为轴旋转而得到的圆锥也可以由扇形卷曲而得到。
2、圆锥的高是两个顶点与底面之间的距离,与圆柱不同,圆锥只有一条高。
3、圆锥的特征:
(1)底面的特征:圆锥的底面一个圆。
(2)侧面的特征:圆锥的侧面是一个曲面。
(3)高的特征 :圆锥有一条高。
4、圆柱的切割:①横切:切面是圆;
②竖切(过顶点和直径直径):切面是等腰三角形,该等腰三角形的高是圆锥的高,底是圆锥的底面直径,面积增加两个等腰三角形的面积,即S增=2rh。
5、圆锥的相关计算公式:底面积:S底=πr
底面周长:C底=πd=2πr
体积:V锥=πr h
知识点03:圆柱和圆锥的关系
1、圆柱与圆锥等底等高,圆柱的体积是圆锥的3倍。
2、圆柱与圆锥等底等体积,圆锥的高是圆柱的3倍。
3、圆柱与圆锥等高等体积,圆锥的底面积(注意:是底面积而不是底面半径)是圆柱的3倍。
4、圆柱与圆锥等底等高,体积相差Sh
拔高训练
一、填空题(共20分)
1.在春季研学活动中,张亮和李明带领同学们动手搭建了一个近似于圆锥形状的野营帐篷。为选择适当的空地,他们测量出该帐篷的底面半径是3米,高是2.4米。搭建该帐篷所需的占地面积是( )平方米,所容纳的空间是( )立方米。
2.一瓶圆柱形的水果罐头,底面周长是25.12cm,高是8cm。这个罐头瓶的容积是( )mL。(罐头瓶的厚度忽略不计)
3.如图,圆柱体队鼓的侧面是由铝片围成的,上、下面蒙的是羊皮。做一个这样的队鼓(接头处不计),至少需要( )平方分米铝皮和( )平方分米羊皮。
4.一个正方体和圆锥的底面积相等,高也相等。已知圆锥的体积是78.5cm3,那么正方体的体积是( )cm3。
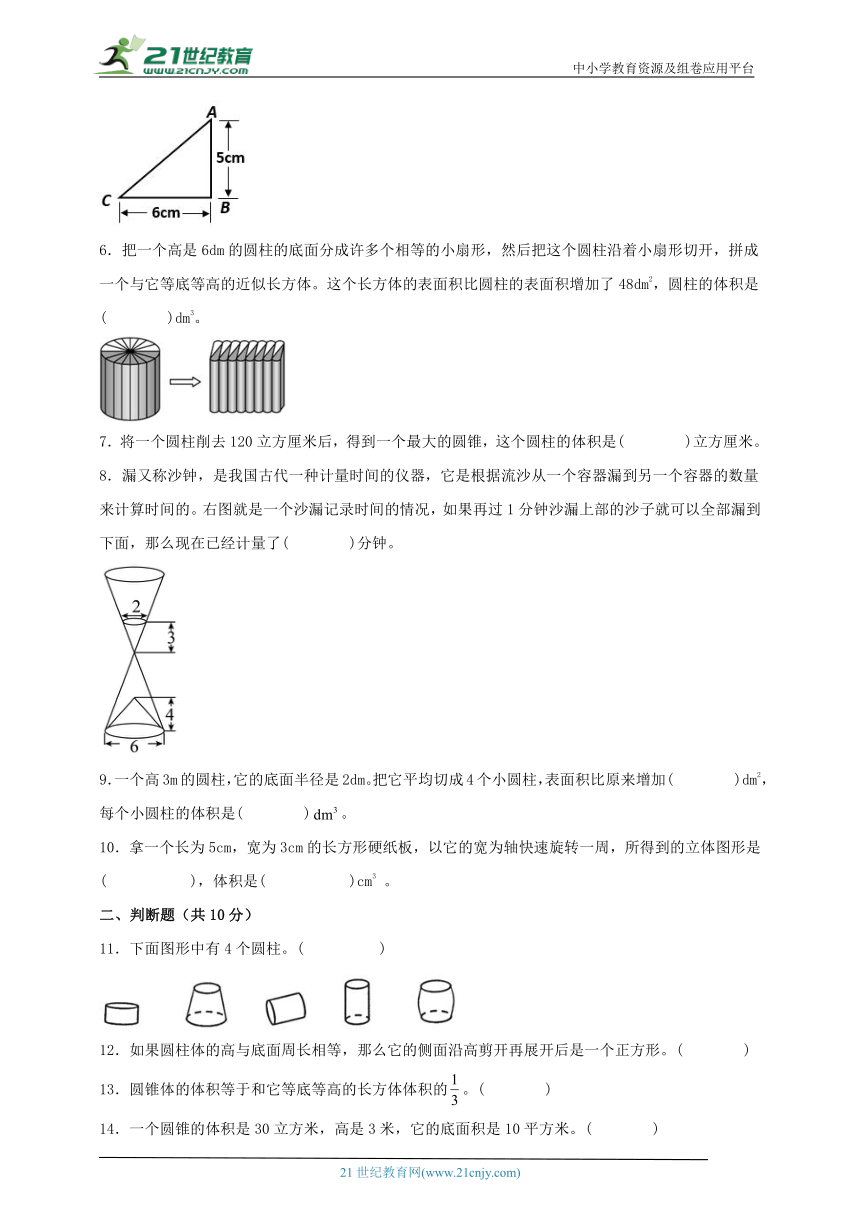
5.如图,在直角三角形ABC中,以AB所在的直线为轴旋转一周,可以得到的立体图形是( ),这个立体图形的体积是( )cm3。
6.把一个高是6dm的圆柱的底面分成许多个相等的小扇形,然后把这个圆柱沿着小扇形切开,拼成一个与它等底等高的近似长方体。这个长方体的表面积比圆柱的表面积增加了48dm2,圆柱的体积是( )dm3。
7.将一个圆柱削去120立方厘米后,得到一个最大的圆锥,这个圆柱的体积是( )立方厘米。
8.漏又称沙钟,是我国古代一种计量时间的仪器,它是根据流沙从一个容器漏到另一个容器的数量来计算时间的。右图就是一个沙漏记录时间的情况,如果再过1分钟沙漏上部的沙子就可以全部漏到下面,那么现在已经计量了( )分钟。
9.一个高3m的圆柱,它的底面半径是2dm。把它平均切成4个小圆柱,表面积比原来增加( )dm2,每个小圆柱的体积是( )。
10.拿一个长为5cm,宽为3cm的长方形硬纸板,以它的宽为轴快速旋转一周,所得到的立体图形是( ),体积是( )cm3 。
二、判断题(共10分)
11.下面图形中有4个圆柱。( )
12.如果圆柱体的高与底面周长相等,那么它的侧面沿高剪开再展开后是一个正方形。( )
13.圆锥体的体积等于和它等底等高的长方体体积的。( )
14.一个圆锥的体积是30立方米,高是3米,它的底面积是10平方米。( )
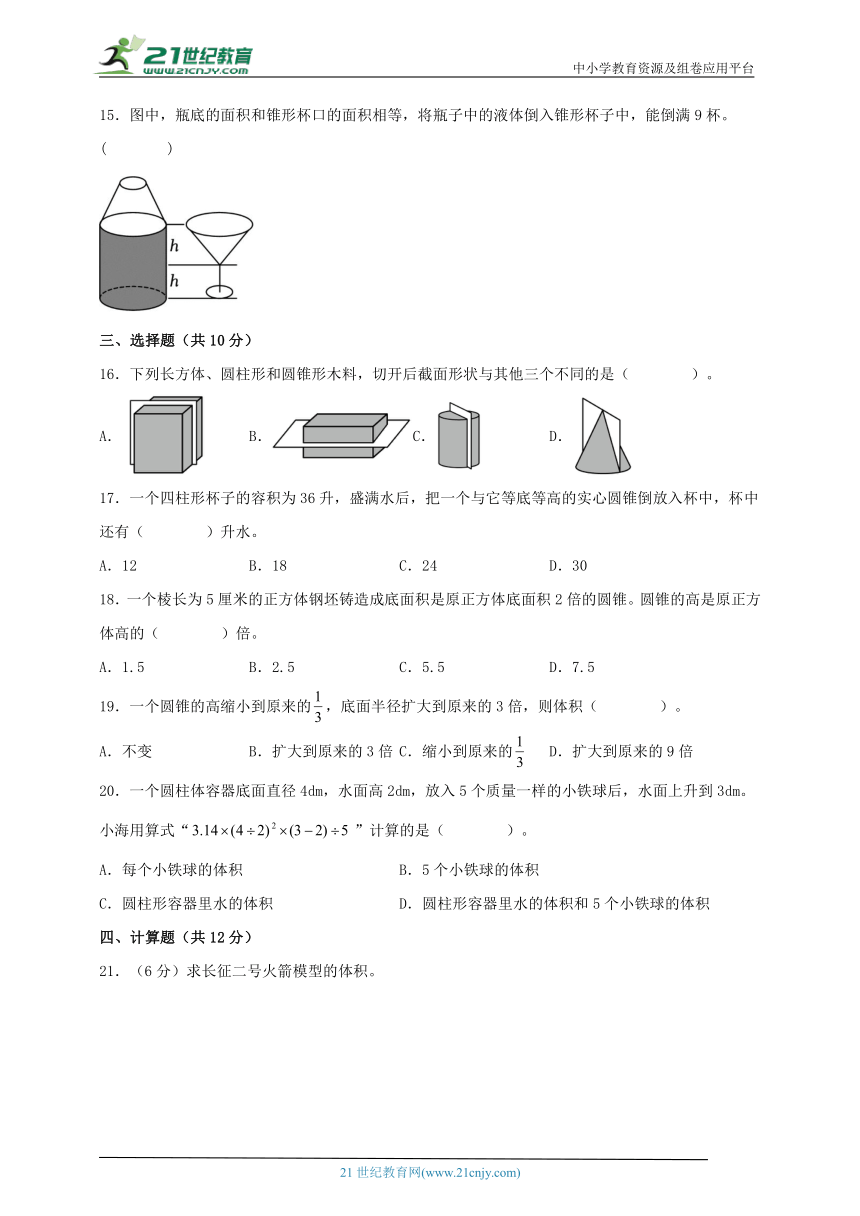
15.图中,瓶底的面积和锥形杯口的面积相等,将瓶子中的液体倒入锥形杯子中,能倒满9杯。( )
三、选择题(共10分)
16.下列长方体、圆柱形和圆锥形木料,切开后截面形状与其他三个不同的是( )。
A. B.C. D.
17.一个四柱形杯子的容积为36升,盛满水后,把一个与它等底等高的实心圆锥倒放入杯中,杯中还有( )升水。
A.12 B.18 C.24 D.30
18.一个棱长为5厘米的正方体钢坯铸造成底面积是原正方体底面积2倍的圆锥。圆锥的高是原正方体高的( )倍。
A.1.5 B.2.5 C.5.5 D.7.5
19.一个圆锥的高缩小到原来的,底面半径扩大到原来的3倍,则体积( )。
A.不变 B.扩大到原来的3倍 C.缩小到原来的 D.扩大到原来的9倍
20.一个圆柱体容器底面直径4dm,水面高2dm,放入5个质量一样的小铁球后,水面上升到3dm。小海用算式“”计算的是( )。
A.每个小铁球的体积 B.5个小铁球的体积
C.圆柱形容器里水的体积 D.圆柱形容器里水的体积和5个小铁球的体积
四、计算题(共12分)
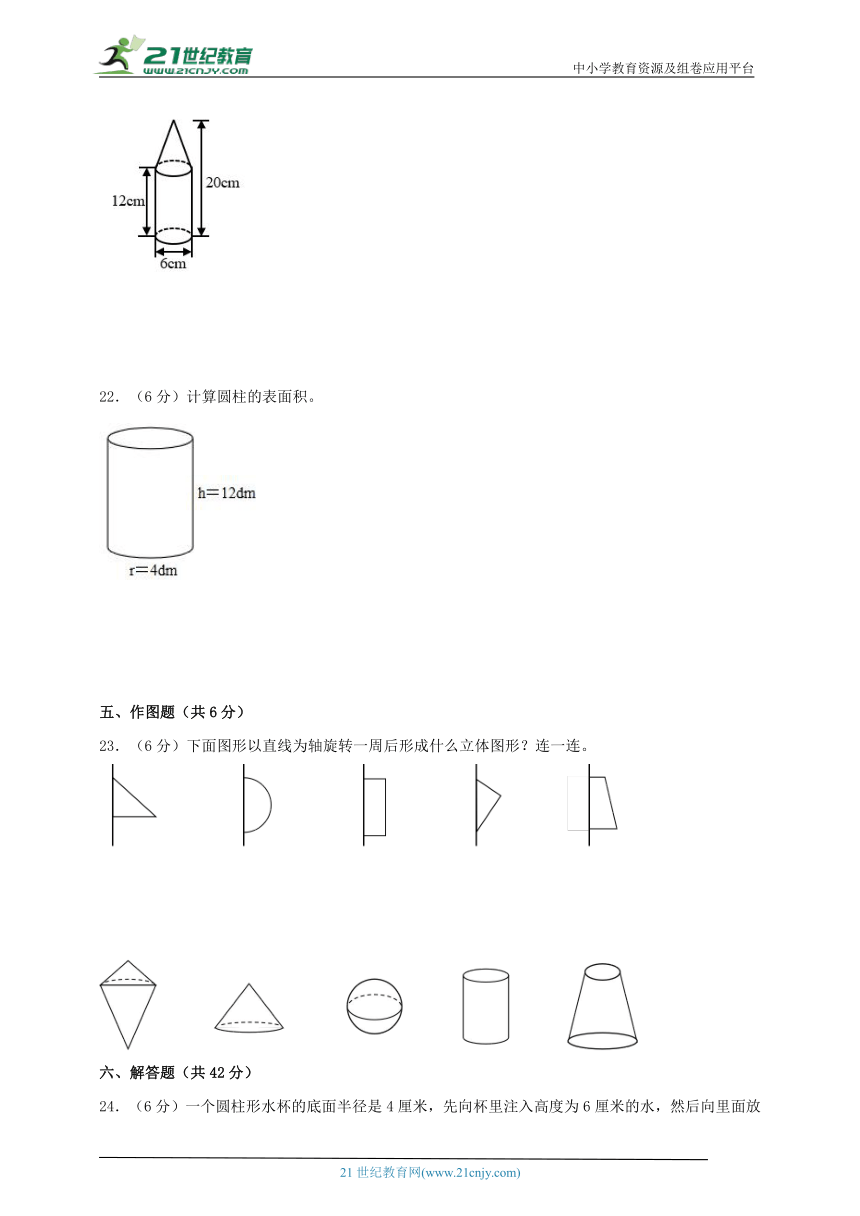
21.(6分)求长征二号火箭模型的体积。
22.(6分)计算圆柱的表面积。
五、作图题(共6分)
23.(6分)下面图形以直线为轴旋转一周后形成什么立体图形?连一连。
六、解答题(共42分)
24.(6分)一个圆柱形水杯的底面半径是4厘米,先向杯里注入高度为6厘米的水,然后向里面放进4个小铁球,小铁球沉没水中后水面上升到8厘米。一个小铁球的体积是多少立方厘米?
25.(6分)在一个棱长是20厘米的正方体密闭容器的下底固定了一个实心圆柱体,容器内盛有4550毫升水,水面恰好没过圆柱体的上底面;如果将容器倒置,那么圆柱体有8厘米露出水面。已知圆柱体的底面积是正方体底面积的,实心圆柱体的体积是多少?
26.(6分)某款奶粉的奶粉桶是圆柱形的铁桶,它的底面周长是37.68厘米,高是2分米,做一个这样的奶粉桶至少需要用铁皮多少平方厘米?(接口处不计)
27.(6分)一款魔术帽,上部分是圆柱形,帽檐部分是一个圆环。制作这顶帽子需要布料多少平方厘米?
28.(6分)一个圆柱形容器里面装有60厘米深的水,从里面量该容器的底面半径为10厘米。调皮的弟弟将一个底面半径为6厘米的圆锥形玩具完全浸没在水中,这时水面上升了3厘米(水未溢出),这个圆锥形玩具的高是多少厘米?
29.(6分)一个酒瓶,底面直径为8厘米,瓶里酒深12厘米,把瓶盖拧紧后倒置(瓶口向下),无水部分高10厘米。你能算出这个酒瓶的容积是多少毫升吗?(酒瓶的厚度忽略不计)
30.(6分)小雨家有6个从里面量得底面积是30厘米、高是10厘米的圆柱形水杯,沏一壶茶水正好能倒满4杯。有一天来了6位客人,小雨沏了一壶茶水,将这壶茶水倒入6个杯中,平均每杯倒多少毫升?
参考答案
1.28.26 22.608
【分析】求搭建该帐篷所需的占地面积,实际是求这个圆锥形状的野营帐篷的底面积,根据圆的面积公式:S=,代入数据即可得解;求所容纳的空间,实际是求这个圆锥形状的野营帐篷的容积,根据圆锥的容积公式:V=Sh,代入数据即可得解。
【详解】3.14×32
=3.14×9
=28.26(平方米)
×28.26×2.4
=9.42×2.4
=22.608(立方米)
即搭建该帐篷所需的占地面积是28.26平方米,所容纳的空间是22.608立方米。
【点睛】此题的解题关键是掌握圆锥的特征、圆锥的底面积以及容积的计算方法。
2.401.92
【分析】已知底面周长是25.12cm,利用圆的周长公式:C=,代入数据求出底面半径,再根据圆柱的容积公式:V=,代入数据即可求出这个罐头瓶的容积。
【详解】25.12÷2÷3.14=4(cm)
3.14×42×8
=3.14×16×8
=401.92(cm3)
=401.92(mL)
即这个罐头瓶的容积是401.92mL。
【点睛】此题的解题关键是利用圆的周长公式以及圆柱的容积公式解决问题。
3. 47.1 56.52
【分析】根据圆柱的侧面积公式:S=πdh,用3.14×6×2.5即可求出圆柱的侧面积;根据圆柱的底面积公式:S=πr2,用3.14×(6÷2)2×2即可求出2个底面积;据此解答。
【详解】3.14×6×2.5=47.1(平方分米)
3.14×(6÷2)2×2
=3.14×32×2
=3.14×9×2
=56.52(平方分米)
做一个这样的队鼓(接头处不计),至少需要47.1平方分米铝皮和56.52平方分米羊皮。
【点睛】本题主要考查了圆柱的表面积公式的灵活应用,要熟练掌握公式。
4.235.5
【分析】根据正方体的体积公式:V=a3,圆锥的体积公式:V=Sh,又因为正方体和圆锥的底面积相等,高也相等,所以该正方体的体积是圆锥的3倍,据此计算即可。
【详解】78.5×3=235.5(cm3)
则正方体的体积是235.5cm3。
【点睛】本题考查正方体和圆锥的体积,熟记公式是解题的关键。
5. 圆锥 188.4
【分析】以三角形的直角边为轴旋转一周,可以得到的立体图形是圆锥,AB边为圆锥的高,BC边为圆锥的底面半径,再根据圆锥的体积公式进行计算即可。
【详解】
所以得到的立体图形是圆锥,这个立体图形的体积是188.4cm3。
【点睛】本题考查圆锥的体积,解答本题的关键是掌握圆锥的体积计算公式。
6.301.44
【分析】观察图形可知,把圆柱沿着小扇形切开,拼成一个与它等底等高的近似长方体,则这个长方体的表面积比圆柱的表面积增加了两个长方形的面积,该长方形的长相当于圆柱的高,长方形的宽相当于圆柱的底面半径,据此求出圆柱的底面半径,再根据圆柱的体积公式:V=πr2h,据此计算即可。
【详解】48÷2÷6
=24÷6
=4(dm)
3.14×42×6
=3.14×16×6
=50.24×6
=301.44(dm3)
则圆柱的体积是301.44dm3。
【点睛】本题考查圆柱的体积,求出圆柱的底面半径是解题的关键。
7.180
【分析】以圆柱的底为底,圆柱的高为高的圆锥是圆柱里面最大的圆锥,当圆柱和圆锥等底等高时,圆柱的体积是圆锥体积的3倍,圆锥的体积是圆柱体积的,把圆柱的体积看作单位“1”,削去部分的体积占圆柱体积的(1-),圆柱的体积=削去部分的体积÷(1-),据此解答。
【详解】120÷(1-)
=120÷
=120×
=180(立方厘米)
所以,这个圆柱的体积是180立方厘米。
【点睛】掌握等底等高的圆柱和圆锥之间的体积关系是解答题目的关键。
8.12
【分析】圆锥的体积,据此先把直径2,高3代入圆锥的体积公式求出上部沙子的体积;再把直径6,高4代入圆锥的体积公式求出下部沙子的体积;再用下部沙子的体积除以上部沙子的体积,求出下部沙子的体积是上部沙子的体积的几倍;因为上部的沙子漏下去需要1分钟,所以下部沙子的体积是上部沙子的体积的几倍就需要几分钟。
【详解】
=
=
=×1
=12×1
=12(分钟)
所以现在已经计量了12分钟。
【点睛】此题主要考查了圆锥的体积计算公式。明确上部和下部沙子的体积间的关系是解决此题的关键。
9. 75.36 94.2
【分析】由高级单位米转化成低级单位分米,用米乘进率10,将高的单位转化成分米。圆柱沿着与底面平行的方向,把它平均切成4个小圆柱,需要切3刀,每刀增加2个圆的面积,则表面积比原来增加了(2×3)个圆的面积,根据圆的面积公式:S=r2,代入数值求出一个圆的面积,再用该面积乘增加的数量,即为增加的表面积;再根据圆柱的体积公式:V=Sh,圆柱的高为3除以4,将数值代入求解即可。
【详解】由分析可得:
2×3=6(个)
3.14×22×6
=3.14×4×6
=12.56×6
=75.36(dm2)
3m=3×10=30dm
30÷4=7.5(dm)
3.14×22×7.5
=3.14×4×7.5
=12.56×7.5
=94.2(dm3)
综上所述:一个高3m的圆柱,它的底面半径是2dm。把它平均切成4个小圆柱,表面积比原来增加75.36dm2,每个小圆柱的体积是94.2dm3。
【点睛】本题考查了圆形的面积公式和圆柱的体积公式的灵活运用,解题的关键是明确切成4个小圆柱,增加了6个圆的面积。
10. 圆柱 235.5
【分析】圆柱是由以长方形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。以长方形的宽为轴快速旋转一周,形成的圆柱,圆柱底面半径=长方形的长,圆柱的高=长方形的宽,根据圆柱体积=底面积×高,列式计算即可。
【详解】3.14×52×3
=3.14×25×3
=235.5(cm3)
所得到的立体图形是圆柱,体积是235.5cm3 。
11.×
【分析】以长方形的一条边所在的直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体就是圆柱,圆柱的底面都是圆,并且大小一样,圆柱的侧面是曲面,同一个圆柱两底面之间的距离都相等,据此解答。
【详解】分析可知,第1个图形、第3个图形、第4个图形是圆柱,一共有3个圆柱。
故答案为:×
【点睛】本题主要考查圆柱的认识,掌握圆柱的特征是解答题目的关键。
12.√
【分析】圆柱的侧面展开图一般是长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高;特殊情况下,圆柱的侧面展开图是正方形,此时圆柱的底面周长和高相等;据此判断。
【详解】如果圆柱体的高与底面周长相等,那么它的侧面沿高剪开再展开后是一个正方形。
原题说法正确。
故答案为:√
【点睛】本题考查圆柱侧面展开图的特点及应用,掌握圆柱的侧面展开图与圆柱的底面周长和高之间的关系是解题的关键。
13.√
【分析】根据题意可知,长方体和圆锥等底等高,可以设出底面积和高,然后分别写出它们的体积公式,最后相除即可得到倍数关系,据此解答。
【详解】解:设长方体和圆锥的底面积为S,高为h,
则长方体的体积是:V=Sh,
圆锥的体积是:V=,
即圆锥体的体积等于和它等底等高的长方体体积的。
故答案为:√
【点睛】此题的解题关键是灵活运用长方体和圆锥的体积公式求解。
14.×
【分析】已知圆锥的体积是30立方米,高是3米,根据圆锥的体积公式:V=Sh,可用3×30÷3求出底面积。
【详解】3×30÷3=30(平方米)
所以底面积是30平方米。
故答案为:×
【点睛】本题主要考查了圆锥体积公式的灵活应用。
15.×
【分析】由图可知,圆柱的底面积和圆锥的底面积相等,把瓶子中的液体看作一个圆柱,圆柱的一半与圆锥等底等高,当圆柱和圆锥等底等高时,圆柱的体积是圆锥体积的3倍,液体的一半倒入锥形杯子中可以倒3杯,那么全部液体可以倒6杯,据此解答。
【详解】分析可知,把瓶内液体的体积看作与锥形杯子等底等高的两部分,一部分倒入锥形杯子中可以倒3杯。
3×2=6(杯)
所以,能倒满6杯。
故答案为:×
【点睛】掌握等底等高的圆柱和圆锥之间的体积关系是解答题目的关键。
16.D
【分析】观察图形可知,长方体无论是横切,还是竖切,切面都是长方形;圆柱沿底面直径切开,切面是长方形;圆锥从顶点到底面直径切开,切面是三角形。据此解答。
【详解】A. 切开后截面是长方形;
B.切开后截面是长方形;
C. 切开后截面是长方形;
D. 切开后截面是三角形。
所以,长方体、圆柱形和圆锥形木料,切开后截面形状与其他三个不同的是圆锥。
故答案为:D
17.C
【分析】由条件“一个与它等底等高的圆锥”可知,圆锥的体积是圆柱体积的,也就是36升的;把圆锥倒放入水中后会排出与它等体积的水,所以杯中剩下的水的体积就是圆柱体积的(1-),也就是36升的(1-),可用乘法列式求得。
【详解】36×(1-)
=36×
=24(升)
则杯中还有24升水。
故答案为:C
18.A
【分析】根据正方体体积=棱长×棱长×棱长,求出钢坯体积,圆锥的高=体积×3÷底面积,求出圆锥的高,再用圆锥的高÷正方体棱长即可。
【详解】5×5×5=125(立方厘米)
125×3÷(5×5×2)
=375÷50
=7.5(厘米)
7.5÷5=1.5
圆锥的高是原正方体高的1.5倍。
故答案为:A
19.B
【分析】根据圆锥的体积公式V=πr2h,以及积的变化规律:一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几”可知:
一个圆锥的高缩小到原来的,则体积除以3;底面半径扩大到原来的3倍,即底面积扩大到原来的3×3=9倍,则体积乘9;最终圆锥的体积÷3×9,体积扩大到原来的3倍,据此举例说明。
【详解】设原来圆锥的底面半径是1,高是3;
原来圆锥的体积:×π×12×3=π
现在圆锥的底面半径是:1×3=3
现在圆锥的高是:3÷3=1
现在圆锥的体积:
×π×32×1
=×π×9×1
=3π
3π÷π=3
即体积扩大到原来的3倍。
故答案为:B
20.A
【分析】分析算式“”,“”求的是底面积,是水面上升的高度,铁球总体积=圆柱底面积×水面上升的高度,因此“”求的是5个小铁球的体积,再除以5是求每个小铁球的体积。
【详解】根据分析,算式“”计算的是每个小铁球的体积。
故答案为:A
21.414.48cm3
【分析】观察图形可知,长征二号火箭模型的体积=圆柱的体积+圆锥的体积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算求解。
【详解】3.14×(6÷2)2×12+×3.14×(6÷2)2×(20-12)
=3.14×9×12+×3.14×9×8
=339.12+75.36
=414.48(cm3)
长征二号火箭模型的体积是414.48cm3。
22.401.92dm2
【分析】圆柱表面积=底面积×2+侧面积,圆柱侧面积=底面周长×高,据此列式计算。
【详解】3.14×42×2+2×3.14×4×12
=3.14×16×2+301.44
=100.48+301.44
=401.92(dm2)
23.图见详解
【分析】一个平面图形围绕一条轴旋转一周,根据圆柱、圆锥以及球体的侧面展开图的特点即可解答。
【详解】作图如下:
【点睛】此题考查了点、线、面、体,考查学生立体图形的空间想象能力及分析问题、解决问题的能力。
24.25.12立方厘米
【分析】由题意可知:4个小铁球的体积就等于上升部分的水的体积,于是可以利用圆柱的体积=底面积×高,求出升高部分的水的体积,从而除以4求出一个小铁球的体积。
【详解】3.14×42×(8-6)÷4
=3.14×16×2÷4
=100.48÷4
=25.12(立方厘米)
答:一个小铁球的体积是25.12立方厘米。
【点睛】此题主要考查某些实物体积的测量方法。
25.650立方厘米
【分析】根据题意可知,圆柱的高度相当于水的高度,根据正方形的面积公式,用20×20即可求出正方体的底面积,已知圆柱体的底面积是正方体底面积的,则把正方体的底面积看作单位“1”,根据分数乘法的意义,用20×20×即可求出圆柱的底面积;假设圆柱的高度是x厘米,因为水面恰好没过圆柱体的上底面,则含有水和圆柱两部分的长方体的高与圆柱等高。根据长方体的体积和圆柱的体积公式,长方体的体积-圆柱的体积=水的体积,可知400x-50x=4550,然后解出方程即可,再根据圆柱的体积公式代入数据解答。
【详解】20×20=400(平方厘米)
400×=50(平方厘米)
4550毫升=4550立方厘米
解:设圆柱的高度是x厘米。
400x-50x=4550
350x=4550
x=4550÷350
x=13
50×13=650(立方厘米)
答:实心圆柱体的体积是650立方厘米。
【点睛】本题主要考查了圆柱的体积公式和长方体体积公式的灵活应用,注意圆柱的高度相当于水的高度。
26.979.68平方厘米
【分析】根据圆柱的表面积=圆柱的侧面积+两个底面的面积,把数据代入公式解答。
【详解】2分米=20厘米
37.68×20+3.14×(37.68÷3.14÷2)2×2
=753.6+3.14×(12÷2)2×2
=753.6+3.14×36×2
=753.6+226.08
=979.68(平方厘米)
答:做一个这样的奶粉桶至少需要用铁皮979.68平方厘米。
【点睛】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
27.2198平方厘米
【分析】通过观察可知制作这顶帽子需要布料就是一个圆柱的侧面积加上一个大圆的面积,根据侧面积=底面周长×高,圆的面积=πr2,代入数值进行计算即可。
【详解】圆柱的侧面积:
3.14×20×15
=62.8×15
=942(平方厘米)
大圆的半径:
(20+10×2)÷2
=40÷2
=20(厘米)
圆的面积:
3.14 ×202
=3.14×400
=1256(平方厘米)
总面积:
942+1256=2198(平方厘米)
答:制作这顶帽子需要布料2198平方厘米。
【点睛】本题考查有关于圆柱的计算及应用。理解题意,找出数量关系,列式计算即可。
28.25厘米
【分析】根据题意可知:圆柱形容器内放入圆锥后,上升部分水的体积等于这个圆锥的体积,根据圆柱的体积公式:,把数据代入公式求出这个圆锥形玩具的体积,再根据圆锥的体积公式:,那么,把数据代入公式解答即可。
【详解】
=3.14×100×3×3÷(3.14×36)
=942×3÷113.04
=2826÷113.04
=25(厘米)
答:这个圆锥形玩具的高是25厘米。
【点睛】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
29.1105.28毫升
【分析】酒瓶的容积=酒的体积+空白部分的容积,用左边酒的体积+右边空白部分的容积即可,圆柱体积=底面积×高,据此列式解答。
【详解】3.14×(8÷2)2×12+3.14×(8÷2)2×10
=3.14×42×12+3.14×42×10
=3.14×16×12+3.14×16×10
=602.88+502.4
=1105.28(立方厘米)
=1105.28(毫升)
答:这个酒瓶的容积是1105.28毫升。
【点睛】关键是利用转化思想,将不规则部分的容积转化为圆柱进行计算。
30.200毫升
【分析】根据V=Sh求出一个水杯可以盛水的体积,再乘4即可求出一壶茶水的体积;根据题意,要将一壶茶水平均倒入6个杯子里,用一壶茶水的体积除以6即可解答。
【详解】30×10×4÷6
=300×4÷6
=200(立方厘米)
=200(毫升)
答:平均每杯倒200毫升。
【点睛】此题的解题关键是先求出一壶茶水的体积是解答本题的关键,再除以6即可解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三单元圆柱与圆锥(知识梳理+拔高训练)二
知识梳理
知识点01:圆柱
1、圆柱的形成:圆柱是以长方形的一边为轴旋转而得到的。
圆柱也可以由长方形卷曲而得到。(两种方式:①以长方形的长为底面周长,宽为高;②以长方形的宽为底面周长,长为高。其中,第一种方式得到的圆柱体体积较大。)
2、圆柱的高是两个底面之间的距离,一个圆柱有无数条高,他们的数值是相等的。
3、圆柱的特征:
(1)底面的特征:圆柱的底面是完全相等的两个圆。
(2)侧面的特征:圆柱的侧面是一个曲面。
(3)高的特征 :圆柱有无数条高。
4、圆柱的切割:①横切:切面是圆,表面积增加 2 倍底面积,即 S增 =2πr ;
②竖切(过直径):切面是长方形(如果 h=2R,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4rh。
5、圆柱的侧面展开图:①沿着高展开,展开图形是长方形,如果 h=2πr,展开图形为正方形;
②不沿着高展开,展开图形是平行四边形或不规则图形;
③无论怎么展开都得不到梯形。
6、圆柱的相关计算公式:底面积 :S底=πr
底面周长:C底=πd=2πr
侧面积:S侧=2πrh
表面积:S表=2S底+S侧=2πr +2πrh
体积:V柱=πr h
知识点02:圆锥
1、圆柱的形成:圆锥是以直角三角形的一直角边为轴旋转而得到的圆锥也可以由扇形卷曲而得到。
2、圆锥的高是两个顶点与底面之间的距离,与圆柱不同,圆锥只有一条高。
3、圆锥的特征:
(1)底面的特征:圆锥的底面一个圆。
(2)侧面的特征:圆锥的侧面是一个曲面。
(3)高的特征 :圆锥有一条高。
4、圆柱的切割:①横切:切面是圆;
②竖切(过顶点和直径直径):切面是等腰三角形,该等腰三角形的高是圆锥的高,底是圆锥的底面直径,面积增加两个等腰三角形的面积,即S增=2rh。
5、圆锥的相关计算公式:底面积:S底=πr
底面周长:C底=πd=2πr
体积:V锥=πr h
知识点03:圆柱和圆锥的关系
1、圆柱与圆锥等底等高,圆柱的体积是圆锥的3倍。
2、圆柱与圆锥等底等体积,圆锥的高是圆柱的3倍。
3、圆柱与圆锥等高等体积,圆锥的底面积(注意:是底面积而不是底面半径)是圆柱的3倍。
4、圆柱与圆锥等底等高,体积相差Sh
拔高训练
一、填空题(共20分)
1.在春季研学活动中,张亮和李明带领同学们动手搭建了一个近似于圆锥形状的野营帐篷。为选择适当的空地,他们测量出该帐篷的底面半径是3米,高是2.4米。搭建该帐篷所需的占地面积是( )平方米,所容纳的空间是( )立方米。
2.一瓶圆柱形的水果罐头,底面周长是25.12cm,高是8cm。这个罐头瓶的容积是( )mL。(罐头瓶的厚度忽略不计)
3.如图,圆柱体队鼓的侧面是由铝片围成的,上、下面蒙的是羊皮。做一个这样的队鼓(接头处不计),至少需要( )平方分米铝皮和( )平方分米羊皮。
4.一个正方体和圆锥的底面积相等,高也相等。已知圆锥的体积是78.5cm3,那么正方体的体积是( )cm3。
5.如图,在直角三角形ABC中,以AB所在的直线为轴旋转一周,可以得到的立体图形是( ),这个立体图形的体积是( )cm3。
6.把一个高是6dm的圆柱的底面分成许多个相等的小扇形,然后把这个圆柱沿着小扇形切开,拼成一个与它等底等高的近似长方体。这个长方体的表面积比圆柱的表面积增加了48dm2,圆柱的体积是( )dm3。
7.将一个圆柱削去120立方厘米后,得到一个最大的圆锥,这个圆柱的体积是( )立方厘米。
8.漏又称沙钟,是我国古代一种计量时间的仪器,它是根据流沙从一个容器漏到另一个容器的数量来计算时间的。右图就是一个沙漏记录时间的情况,如果再过1分钟沙漏上部的沙子就可以全部漏到下面,那么现在已经计量了( )分钟。
9.一个高3m的圆柱,它的底面半径是2dm。把它平均切成4个小圆柱,表面积比原来增加( )dm2,每个小圆柱的体积是( )。
10.拿一个长为5cm,宽为3cm的长方形硬纸板,以它的宽为轴快速旋转一周,所得到的立体图形是( ),体积是( )cm3 。
二、判断题(共10分)
11.下面图形中有4个圆柱。( )
12.如果圆柱体的高与底面周长相等,那么它的侧面沿高剪开再展开后是一个正方形。( )
13.圆锥体的体积等于和它等底等高的长方体体积的。( )
14.一个圆锥的体积是30立方米,高是3米,它的底面积是10平方米。( )
15.图中,瓶底的面积和锥形杯口的面积相等,将瓶子中的液体倒入锥形杯子中,能倒满9杯。( )
三、选择题(共10分)
16.下列长方体、圆柱形和圆锥形木料,切开后截面形状与其他三个不同的是( )。
A. B.C. D.
17.一个四柱形杯子的容积为36升,盛满水后,把一个与它等底等高的实心圆锥倒放入杯中,杯中还有( )升水。
A.12 B.18 C.24 D.30
18.一个棱长为5厘米的正方体钢坯铸造成底面积是原正方体底面积2倍的圆锥。圆锥的高是原正方体高的( )倍。
A.1.5 B.2.5 C.5.5 D.7.5
19.一个圆锥的高缩小到原来的,底面半径扩大到原来的3倍,则体积( )。
A.不变 B.扩大到原来的3倍 C.缩小到原来的 D.扩大到原来的9倍
20.一个圆柱体容器底面直径4dm,水面高2dm,放入5个质量一样的小铁球后,水面上升到3dm。小海用算式“”计算的是( )。
A.每个小铁球的体积 B.5个小铁球的体积
C.圆柱形容器里水的体积 D.圆柱形容器里水的体积和5个小铁球的体积
四、计算题(共12分)
21.(6分)求长征二号火箭模型的体积。
22.(6分)计算圆柱的表面积。
五、作图题(共6分)
23.(6分)下面图形以直线为轴旋转一周后形成什么立体图形?连一连。
六、解答题(共42分)
24.(6分)一个圆柱形水杯的底面半径是4厘米,先向杯里注入高度为6厘米的水,然后向里面放进4个小铁球,小铁球沉没水中后水面上升到8厘米。一个小铁球的体积是多少立方厘米?
25.(6分)在一个棱长是20厘米的正方体密闭容器的下底固定了一个实心圆柱体,容器内盛有4550毫升水,水面恰好没过圆柱体的上底面;如果将容器倒置,那么圆柱体有8厘米露出水面。已知圆柱体的底面积是正方体底面积的,实心圆柱体的体积是多少?
26.(6分)某款奶粉的奶粉桶是圆柱形的铁桶,它的底面周长是37.68厘米,高是2分米,做一个这样的奶粉桶至少需要用铁皮多少平方厘米?(接口处不计)
27.(6分)一款魔术帽,上部分是圆柱形,帽檐部分是一个圆环。制作这顶帽子需要布料多少平方厘米?
28.(6分)一个圆柱形容器里面装有60厘米深的水,从里面量该容器的底面半径为10厘米。调皮的弟弟将一个底面半径为6厘米的圆锥形玩具完全浸没在水中,这时水面上升了3厘米(水未溢出),这个圆锥形玩具的高是多少厘米?
29.(6分)一个酒瓶,底面直径为8厘米,瓶里酒深12厘米,把瓶盖拧紧后倒置(瓶口向下),无水部分高10厘米。你能算出这个酒瓶的容积是多少毫升吗?(酒瓶的厚度忽略不计)
30.(6分)小雨家有6个从里面量得底面积是30厘米、高是10厘米的圆柱形水杯,沏一壶茶水正好能倒满4杯。有一天来了6位客人,小雨沏了一壶茶水,将这壶茶水倒入6个杯中,平均每杯倒多少毫升?
参考答案
1.28.26 22.608
【分析】求搭建该帐篷所需的占地面积,实际是求这个圆锥形状的野营帐篷的底面积,根据圆的面积公式:S=,代入数据即可得解;求所容纳的空间,实际是求这个圆锥形状的野营帐篷的容积,根据圆锥的容积公式:V=Sh,代入数据即可得解。
【详解】3.14×32
=3.14×9
=28.26(平方米)
×28.26×2.4
=9.42×2.4
=22.608(立方米)
即搭建该帐篷所需的占地面积是28.26平方米,所容纳的空间是22.608立方米。
【点睛】此题的解题关键是掌握圆锥的特征、圆锥的底面积以及容积的计算方法。
2.401.92
【分析】已知底面周长是25.12cm,利用圆的周长公式:C=,代入数据求出底面半径,再根据圆柱的容积公式:V=,代入数据即可求出这个罐头瓶的容积。
【详解】25.12÷2÷3.14=4(cm)
3.14×42×8
=3.14×16×8
=401.92(cm3)
=401.92(mL)
即这个罐头瓶的容积是401.92mL。
【点睛】此题的解题关键是利用圆的周长公式以及圆柱的容积公式解决问题。
3. 47.1 56.52
【分析】根据圆柱的侧面积公式:S=πdh,用3.14×6×2.5即可求出圆柱的侧面积;根据圆柱的底面积公式:S=πr2,用3.14×(6÷2)2×2即可求出2个底面积;据此解答。
【详解】3.14×6×2.5=47.1(平方分米)
3.14×(6÷2)2×2
=3.14×32×2
=3.14×9×2
=56.52(平方分米)
做一个这样的队鼓(接头处不计),至少需要47.1平方分米铝皮和56.52平方分米羊皮。
【点睛】本题主要考查了圆柱的表面积公式的灵活应用,要熟练掌握公式。
4.235.5
【分析】根据正方体的体积公式:V=a3,圆锥的体积公式:V=Sh,又因为正方体和圆锥的底面积相等,高也相等,所以该正方体的体积是圆锥的3倍,据此计算即可。
【详解】78.5×3=235.5(cm3)
则正方体的体积是235.5cm3。
【点睛】本题考查正方体和圆锥的体积,熟记公式是解题的关键。
5. 圆锥 188.4
【分析】以三角形的直角边为轴旋转一周,可以得到的立体图形是圆锥,AB边为圆锥的高,BC边为圆锥的底面半径,再根据圆锥的体积公式进行计算即可。
【详解】
所以得到的立体图形是圆锥,这个立体图形的体积是188.4cm3。
【点睛】本题考查圆锥的体积,解答本题的关键是掌握圆锥的体积计算公式。
6.301.44
【分析】观察图形可知,把圆柱沿着小扇形切开,拼成一个与它等底等高的近似长方体,则这个长方体的表面积比圆柱的表面积增加了两个长方形的面积,该长方形的长相当于圆柱的高,长方形的宽相当于圆柱的底面半径,据此求出圆柱的底面半径,再根据圆柱的体积公式:V=πr2h,据此计算即可。
【详解】48÷2÷6
=24÷6
=4(dm)
3.14×42×6
=3.14×16×6
=50.24×6
=301.44(dm3)
则圆柱的体积是301.44dm3。
【点睛】本题考查圆柱的体积,求出圆柱的底面半径是解题的关键。
7.180
【分析】以圆柱的底为底,圆柱的高为高的圆锥是圆柱里面最大的圆锥,当圆柱和圆锥等底等高时,圆柱的体积是圆锥体积的3倍,圆锥的体积是圆柱体积的,把圆柱的体积看作单位“1”,削去部分的体积占圆柱体积的(1-),圆柱的体积=削去部分的体积÷(1-),据此解答。
【详解】120÷(1-)
=120÷
=120×
=180(立方厘米)
所以,这个圆柱的体积是180立方厘米。
【点睛】掌握等底等高的圆柱和圆锥之间的体积关系是解答题目的关键。
8.12
【分析】圆锥的体积,据此先把直径2,高3代入圆锥的体积公式求出上部沙子的体积;再把直径6,高4代入圆锥的体积公式求出下部沙子的体积;再用下部沙子的体积除以上部沙子的体积,求出下部沙子的体积是上部沙子的体积的几倍;因为上部的沙子漏下去需要1分钟,所以下部沙子的体积是上部沙子的体积的几倍就需要几分钟。
【详解】
=
=
=×1
=12×1
=12(分钟)
所以现在已经计量了12分钟。
【点睛】此题主要考查了圆锥的体积计算公式。明确上部和下部沙子的体积间的关系是解决此题的关键。
9. 75.36 94.2
【分析】由高级单位米转化成低级单位分米,用米乘进率10,将高的单位转化成分米。圆柱沿着与底面平行的方向,把它平均切成4个小圆柱,需要切3刀,每刀增加2个圆的面积,则表面积比原来增加了(2×3)个圆的面积,根据圆的面积公式:S=r2,代入数值求出一个圆的面积,再用该面积乘增加的数量,即为增加的表面积;再根据圆柱的体积公式:V=Sh,圆柱的高为3除以4,将数值代入求解即可。
【详解】由分析可得:
2×3=6(个)
3.14×22×6
=3.14×4×6
=12.56×6
=75.36(dm2)
3m=3×10=30dm
30÷4=7.5(dm)
3.14×22×7.5
=3.14×4×7.5
=12.56×7.5
=94.2(dm3)
综上所述:一个高3m的圆柱,它的底面半径是2dm。把它平均切成4个小圆柱,表面积比原来增加75.36dm2,每个小圆柱的体积是94.2dm3。
【点睛】本题考查了圆形的面积公式和圆柱的体积公式的灵活运用,解题的关键是明确切成4个小圆柱,增加了6个圆的面积。
10. 圆柱 235.5
【分析】圆柱是由以长方形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。以长方形的宽为轴快速旋转一周,形成的圆柱,圆柱底面半径=长方形的长,圆柱的高=长方形的宽,根据圆柱体积=底面积×高,列式计算即可。
【详解】3.14×52×3
=3.14×25×3
=235.5(cm3)
所得到的立体图形是圆柱,体积是235.5cm3 。
11.×
【分析】以长方形的一条边所在的直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体就是圆柱,圆柱的底面都是圆,并且大小一样,圆柱的侧面是曲面,同一个圆柱两底面之间的距离都相等,据此解答。
【详解】分析可知,第1个图形、第3个图形、第4个图形是圆柱,一共有3个圆柱。
故答案为:×
【点睛】本题主要考查圆柱的认识,掌握圆柱的特征是解答题目的关键。
12.√
【分析】圆柱的侧面展开图一般是长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高;特殊情况下,圆柱的侧面展开图是正方形,此时圆柱的底面周长和高相等;据此判断。
【详解】如果圆柱体的高与底面周长相等,那么它的侧面沿高剪开再展开后是一个正方形。
原题说法正确。
故答案为:√
【点睛】本题考查圆柱侧面展开图的特点及应用,掌握圆柱的侧面展开图与圆柱的底面周长和高之间的关系是解题的关键。
13.√
【分析】根据题意可知,长方体和圆锥等底等高,可以设出底面积和高,然后分别写出它们的体积公式,最后相除即可得到倍数关系,据此解答。
【详解】解:设长方体和圆锥的底面积为S,高为h,
则长方体的体积是:V=Sh,
圆锥的体积是:V=,
即圆锥体的体积等于和它等底等高的长方体体积的。
故答案为:√
【点睛】此题的解题关键是灵活运用长方体和圆锥的体积公式求解。
14.×
【分析】已知圆锥的体积是30立方米,高是3米,根据圆锥的体积公式:V=Sh,可用3×30÷3求出底面积。
【详解】3×30÷3=30(平方米)
所以底面积是30平方米。
故答案为:×
【点睛】本题主要考查了圆锥体积公式的灵活应用。
15.×
【分析】由图可知,圆柱的底面积和圆锥的底面积相等,把瓶子中的液体看作一个圆柱,圆柱的一半与圆锥等底等高,当圆柱和圆锥等底等高时,圆柱的体积是圆锥体积的3倍,液体的一半倒入锥形杯子中可以倒3杯,那么全部液体可以倒6杯,据此解答。
【详解】分析可知,把瓶内液体的体积看作与锥形杯子等底等高的两部分,一部分倒入锥形杯子中可以倒3杯。
3×2=6(杯)
所以,能倒满6杯。
故答案为:×
【点睛】掌握等底等高的圆柱和圆锥之间的体积关系是解答题目的关键。
16.D
【分析】观察图形可知,长方体无论是横切,还是竖切,切面都是长方形;圆柱沿底面直径切开,切面是长方形;圆锥从顶点到底面直径切开,切面是三角形。据此解答。
【详解】A. 切开后截面是长方形;
B.切开后截面是长方形;
C. 切开后截面是长方形;
D. 切开后截面是三角形。
所以,长方体、圆柱形和圆锥形木料,切开后截面形状与其他三个不同的是圆锥。
故答案为:D
17.C
【分析】由条件“一个与它等底等高的圆锥”可知,圆锥的体积是圆柱体积的,也就是36升的;把圆锥倒放入水中后会排出与它等体积的水,所以杯中剩下的水的体积就是圆柱体积的(1-),也就是36升的(1-),可用乘法列式求得。
【详解】36×(1-)
=36×
=24(升)
则杯中还有24升水。
故答案为:C
18.A
【分析】根据正方体体积=棱长×棱长×棱长,求出钢坯体积,圆锥的高=体积×3÷底面积,求出圆锥的高,再用圆锥的高÷正方体棱长即可。
【详解】5×5×5=125(立方厘米)
125×3÷(5×5×2)
=375÷50
=7.5(厘米)
7.5÷5=1.5
圆锥的高是原正方体高的1.5倍。
故答案为:A
19.B
【分析】根据圆锥的体积公式V=πr2h,以及积的变化规律:一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几”可知:
一个圆锥的高缩小到原来的,则体积除以3;底面半径扩大到原来的3倍,即底面积扩大到原来的3×3=9倍,则体积乘9;最终圆锥的体积÷3×9,体积扩大到原来的3倍,据此举例说明。
【详解】设原来圆锥的底面半径是1,高是3;
原来圆锥的体积:×π×12×3=π
现在圆锥的底面半径是:1×3=3
现在圆锥的高是:3÷3=1
现在圆锥的体积:
×π×32×1
=×π×9×1
=3π
3π÷π=3
即体积扩大到原来的3倍。
故答案为:B
20.A
【分析】分析算式“”,“”求的是底面积,是水面上升的高度,铁球总体积=圆柱底面积×水面上升的高度,因此“”求的是5个小铁球的体积,再除以5是求每个小铁球的体积。
【详解】根据分析,算式“”计算的是每个小铁球的体积。
故答案为:A
21.414.48cm3
【分析】观察图形可知,长征二号火箭模型的体积=圆柱的体积+圆锥的体积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算求解。
【详解】3.14×(6÷2)2×12+×3.14×(6÷2)2×(20-12)
=3.14×9×12+×3.14×9×8
=339.12+75.36
=414.48(cm3)
长征二号火箭模型的体积是414.48cm3。
22.401.92dm2
【分析】圆柱表面积=底面积×2+侧面积,圆柱侧面积=底面周长×高,据此列式计算。
【详解】3.14×42×2+2×3.14×4×12
=3.14×16×2+301.44
=100.48+301.44
=401.92(dm2)
23.图见详解
【分析】一个平面图形围绕一条轴旋转一周,根据圆柱、圆锥以及球体的侧面展开图的特点即可解答。
【详解】作图如下:
【点睛】此题考查了点、线、面、体,考查学生立体图形的空间想象能力及分析问题、解决问题的能力。
24.25.12立方厘米
【分析】由题意可知:4个小铁球的体积就等于上升部分的水的体积,于是可以利用圆柱的体积=底面积×高,求出升高部分的水的体积,从而除以4求出一个小铁球的体积。
【详解】3.14×42×(8-6)÷4
=3.14×16×2÷4
=100.48÷4
=25.12(立方厘米)
答:一个小铁球的体积是25.12立方厘米。
【点睛】此题主要考查某些实物体积的测量方法。
25.650立方厘米
【分析】根据题意可知,圆柱的高度相当于水的高度,根据正方形的面积公式,用20×20即可求出正方体的底面积,已知圆柱体的底面积是正方体底面积的,则把正方体的底面积看作单位“1”,根据分数乘法的意义,用20×20×即可求出圆柱的底面积;假设圆柱的高度是x厘米,因为水面恰好没过圆柱体的上底面,则含有水和圆柱两部分的长方体的高与圆柱等高。根据长方体的体积和圆柱的体积公式,长方体的体积-圆柱的体积=水的体积,可知400x-50x=4550,然后解出方程即可,再根据圆柱的体积公式代入数据解答。
【详解】20×20=400(平方厘米)
400×=50(平方厘米)
4550毫升=4550立方厘米
解:设圆柱的高度是x厘米。
400x-50x=4550
350x=4550
x=4550÷350
x=13
50×13=650(立方厘米)
答:实心圆柱体的体积是650立方厘米。
【点睛】本题主要考查了圆柱的体积公式和长方体体积公式的灵活应用,注意圆柱的高度相当于水的高度。
26.979.68平方厘米
【分析】根据圆柱的表面积=圆柱的侧面积+两个底面的面积,把数据代入公式解答。
【详解】2分米=20厘米
37.68×20+3.14×(37.68÷3.14÷2)2×2
=753.6+3.14×(12÷2)2×2
=753.6+3.14×36×2
=753.6+226.08
=979.68(平方厘米)
答:做一个这样的奶粉桶至少需要用铁皮979.68平方厘米。
【点睛】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
27.2198平方厘米
【分析】通过观察可知制作这顶帽子需要布料就是一个圆柱的侧面积加上一个大圆的面积,根据侧面积=底面周长×高,圆的面积=πr2,代入数值进行计算即可。
【详解】圆柱的侧面积:
3.14×20×15
=62.8×15
=942(平方厘米)
大圆的半径:
(20+10×2)÷2
=40÷2
=20(厘米)
圆的面积:
3.14 ×202
=3.14×400
=1256(平方厘米)
总面积:
942+1256=2198(平方厘米)
答:制作这顶帽子需要布料2198平方厘米。
【点睛】本题考查有关于圆柱的计算及应用。理解题意,找出数量关系,列式计算即可。
28.25厘米
【分析】根据题意可知:圆柱形容器内放入圆锥后,上升部分水的体积等于这个圆锥的体积,根据圆柱的体积公式:,把数据代入公式求出这个圆锥形玩具的体积,再根据圆锥的体积公式:,那么,把数据代入公式解答即可。
【详解】
=3.14×100×3×3÷(3.14×36)
=942×3÷113.04
=2826÷113.04
=25(厘米)
答:这个圆锥形玩具的高是25厘米。
【点睛】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
29.1105.28毫升
【分析】酒瓶的容积=酒的体积+空白部分的容积,用左边酒的体积+右边空白部分的容积即可,圆柱体积=底面积×高,据此列式解答。
【详解】3.14×(8÷2)2×12+3.14×(8÷2)2×10
=3.14×42×12+3.14×42×10
=3.14×16×12+3.14×16×10
=602.88+502.4
=1105.28(立方厘米)
=1105.28(毫升)
答:这个酒瓶的容积是1105.28毫升。
【点睛】关键是利用转化思想,将不规则部分的容积转化为圆柱进行计算。
30.200毫升
【分析】根据V=Sh求出一个水杯可以盛水的体积,再乘4即可求出一壶茶水的体积;根据题意,要将一壶茶水平均倒入6个杯子里,用一壶茶水的体积除以6即可解答。
【详解】30×10×4÷6
=300×4÷6
=200(立方厘米)
=200(毫升)
答:平均每杯倒200毫升。
【点睛】此题的解题关键是先求出一壶茶水的体积是解答本题的关键,再除以6即可解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
