2025年九年级中考数学三轮冲刺练习二次函数中的角度问题(含答案)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺练习二次函数中的角度问题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 17:58:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺练习二次函数中的角度问题
1.如图,抛物线与y=ax2+bx+3与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C.顶点为(1,4).直线y=3x+7与x,y轴分别相交于点D,E,与直线BC相交于点F.
(1)求该抛物线对应的函数表达式;
(2)请探究在第三象限内的抛物线上是否存在点P,使得∠PBF=∠DFB?若存在,求出点P的坐标;若不存在,说明理由.
2.已知在平面直角坐标系xOy中,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上.现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线经过点O和D.
(1)求点D的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否存在点P,使得∠POB=∠BAO?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.
3.已知点B(5,0),点C(4,3)都在抛物线y=﹣x2+bx+c上,其中点A是抛物线与x轴的交点,点D是抛物线的顶点,连接AD,CD.
(1)求抛物线的解析式;
(2)求∠ACD的度数;
(3)点P是y轴上的一个动点,当∠PCA=∠CAD时,直接写出P点坐标.
4.已知抛物线y=ax2+bx+c(a>0)与x轴左、右交点分别为A、B,与y轴负半轴交于点C,坐标原点为O,若OB=OC=3OA,S△ABC=6,点P是抛物线上的动点(点P在y轴右侧).
(1)求抛物线的解析式;
(2)D是线段OC的中点,
①当∠OPC=45°时,请求出点P的坐标;
②当∠OPC=∠OAD时,请求出点P的坐标.
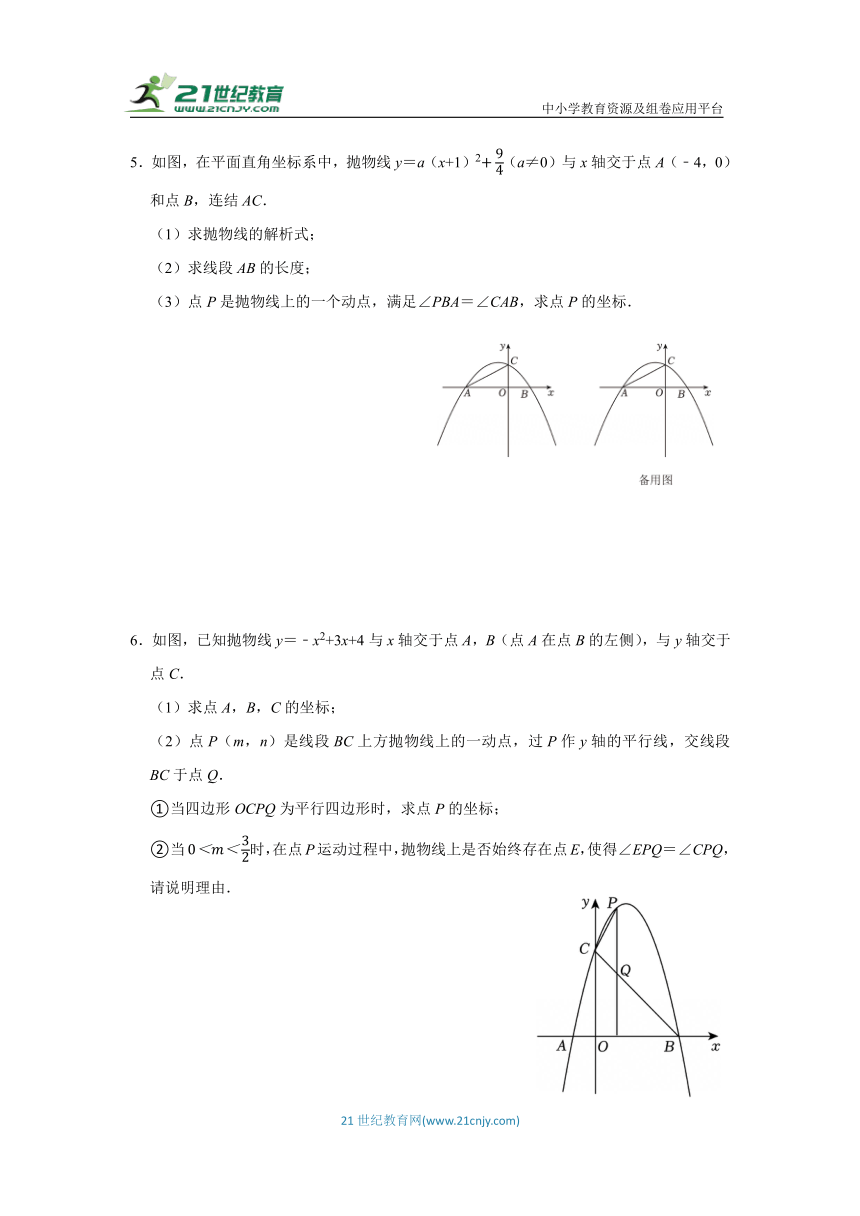
5.如图,在平面直角坐标系中,抛物线y=a(x+1)2(a≠0)与x轴交于点A(﹣4,0)和点B,连结AC.
(1)求抛物线的解析式;
(2)求线段AB的长度;
(3)点P是抛物线上的一个动点,满足∠PBA=∠CAB,求点P的坐标.
6.如图,已知抛物线y=﹣x2+3x+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)点P(m,n)是线段BC上方抛物线上的一动点,过P作y轴的平行线,交线段BC于点Q.
①当四边形OCPQ为平行四边形时,求点P的坐标;
②当时,在点P运动过程中,抛物线上是否始终存在点E,使得∠EPQ=∠CPQ,请说明理由.
7.如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,抛物线y=﹣x2+bx+c经过点B、C,与x轴另一交点为A.
(1)求抛物线的解析式;
(2)若点M是抛物线上的一点,使得S△MBC=S△OBC,请求出点M的坐标;
(3)点D(2,m)在第一象限的抛物线上,连接BD.在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P的坐标;如果不存在,请说明理由.
8.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3与x轴分别交于点A(﹣1,0)、点B(4,0),与y轴交于点C.点P是第一象限的抛物线上一动点.
(1)求抛物线的表达式;
(2)如图,连接PC,当∠PCB=2∠CBA时,求点P的坐标;
(3)如图,过点P作PD⊥BC于点D,求的最大值.
9.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C(0,3),且经过点D(4,﹣5).
(1)求抛物线的解析式;
(2)点P在抛物线上,过P作PE∥y轴,交直线CD于点E,若以P、E、O、C为顶点的四边形是平行四边形,求点P的横坐标;
(3)抛物线上是否存在点Q,使∠QCD=45°.若存在,请直接写出点Q的坐标;若不存在,请说明理由.
10.如图,抛物线y=﹣x2+bx+c经过A(4,0),C(﹣1,0)两点,与y轴交于点B,P为第一象限抛物线上的动点,连接AB、BC、PA、PC,PC与AB相交于点Q.
(1)求抛物线的解析式;
(2)设△APQ的面积为S1,△BCQ的面积为S2,当S1﹣S2=5时,求点P的坐标;
(3)抛物线上存在点P,满足∠PAB+∠CBO=45°,则点P的坐标为 .
11.如图,在平面直角坐标系xOy中,已知抛物线y=﹣x2+bx+3与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,联结AC,tan∠CAO=3,抛物线的顶点为点D.
(1)求b的值和点D的坐标;
(2)点P是抛物线上一点(不与点B重合),点P关于x轴的对称点恰好在直线BC上.
①求点P的坐标;
②点M是抛物线上一点且在对称轴左侧,联结BM,如果∠MBP=∠ABD,求点M的坐标.
12.已知:抛物线y=x2﹣bx﹣3交x、y轴于A、B(3,0),交y轴于C,顶点为D,M为抛物线上动点.
(1)求抛物线的解析式;
(2)在M运动过程中,连OM,当∠DOM=45°时,求M点坐标;
(3)随着M运动到第一象限,如图(2)直线AM交对称轴于E,直线MB交对称轴于F,若对称轴交x轴于H,求HF﹣HE的值.
13.如图,在平面直角坐标系中,抛物线与x轴交于点A,B,其中点B的坐标为(4,0),与y轴交于点C(0,2).
(1)求抛物线和直线BC的函数表达式;
(2)点P是直线BC上方的抛物线上一个动点,当△PBC面积最大时,求P点的坐标;
(3)连接B和(2)中求出的点P,点Q位于直线BP下方且在抛物线上,若∠PBQ=45°,求点Q的坐标.
14.如图,抛物线yx2+bx+c与x轴交于A,B两点,与y轴交于点C,点A坐标为(﹣1,0),点B坐标为(3,0).
(1)求此抛物线的函数解析式.
(2)点P是直线BC上方抛物线上一个动点,过点P作x轴的垂线交直线BC于点D,过点P作y轴的垂线,垂足为点E,求2PD+PE的最大值,及此时P点的坐标.
(3)点M为该抛物线上的点,当∠MCB=45°时,请直接写出满足条件的点M的坐标.
15.如图,在平面直角坐标系中,已知抛物线y=﹣x2+bx+c与x轴交于A,B(4,0)两点,与y轴交于点C,点D(3,4)在抛物线上,点P是抛物线上一动点.
(1)求该抛物线的解析式;
(2)连接BC,若BC上方抛物线上有一点P,且P到直线BC的距离为,求点P的坐标;
(3)如图,连接AC,BC,抛物线上是否存在点P,使∠CBP+∠ACO=45°?若存在,请直接写出点P的坐标;若不存在,请说明理由.
16.二次函数y=ax2+bx+4(a≠0)的图象经过点A(﹣4,0),B(1,0),与y轴交于点C,点P为第二象限内抛物线上一点,连接BP、AC,交于点Q,过点P作PD⊥x轴于点D.
(1)求二次函数的表达式;
(2)连接BC,当∠DPB=2∠BCO时,求直线BP的表达式;
(3)请判断:是否有最大值,如有请求出有最大值时点P的坐标,如没有请说明理由.
17.如图,抛物线yx2+bx+c与x轴交于A(﹣1,0),B(4,0),与y轴交于点C.连接AC,BC,点P在抛物线上运动.
(1)求抛物线的表达式;
(2)如图①,若点P在第四象限,点Q在PA的延长线上,当∠CAQ=∠CBA+45°时,求点P的坐标;
(3)如图②,若点P在第一象限,直线AP交BC于点F,过点P作x轴的垂线交BC于点H,当△PFH为等腰三角形时,求线段PH的长.
18.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+4(a≠0)经过点A(﹣2,0)和点B(4,0).
(1)求这条抛物线所对应的函数表达式;
(2)点P为该抛物线上一点(不与点C重合),直线CP将△ABC的面积分成2:1两部分,求点P的坐标;
(3)点M从点C出发,以每秒1个单位的速度沿y轴移动,运动时间为t秒,当∠OCA=∠OCB﹣∠OMA时,求t的值.
19.如图,抛物线yx2x+4与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.
(1)A,B,C三点的坐标为 , , .
(2)连接AP,交线段BC于点D,
①当CP与x轴平行时,求的值;
②当CP与x轴不平行时,求的最大值;
(3)连接CP,是否存在点P,使得∠BCO+2∠PCB=90°,若存在,求m的值,若不存在,请说明理由.
20.如图,抛物线y=ax2+bx+c(a≠0)经过坐标原点O,且顶点为A(2,﹣4).
(1)求抛物线的表达式;
(2)设抛物线与x轴正半轴的交点为B,点P位于抛物线上且在x轴下方,连接OA、PB,若∠AOB+∠PBO=90°,求点P的坐标.
21.如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于两点A(﹣3,0),B(4,0),与y轴交于点C(0,4).
(1)求此抛物线的解析式;
(2)已知抛物线上有一点P(x0,y0),其中y0<0,若∠CAO+∠ABP=90°,求x0的值;
(3)若点D,E分别是线段AC,AB上的动点,且AE=2CD,求CE+2BD的最小值.
参考答案
1.【解答】解:(1)∵抛物线与y=ax2+bx+3的顶点为(1,4),
∴y=ax2+bx+3=a(x﹣1)2+4,
由题意得:,
解得:,
∴抛物线的表达式为y=﹣x2+2x+3;
(2)在第三象限内的抛物线上存在点P,使得∠PBF=∠DFB;理由如下:
∵直线y=3x+7与x,y轴分别相交于点D,E,
∴当y=0时,3x+7=0,
解得,
∴点D的坐标为.
抛物线与y=﹣x2+2x+3与x轴相交于A,B两点(点A在点B的左侧),
当y=0时得:﹣x2+2x+3=0,
解得x1=﹣1,x2=3,
∴点A的坐标为(﹣1,0),点B的坐标为(3,0),
在y=﹣x2+2x+3中,当x=0时,y=3,
∴点C的坐标为(0,3),
设直线BC的解析式为y=sx+t,将点B,点C的坐标代入得:
,
解得:,
∴直线BC的表达式为y=﹣x+3,
联立得:,
解得,
∴点F的坐标为(﹣1,4).
连接FA,过点P作PM⊥x轴,垂足为M,
由题知FA⊥x轴,,AF=4,,
设点P的坐标为(m,﹣m2+2m+3),
,
当∠PBF=∠DFB时,,
解得,m2=3(舍去),
点P的坐标为.
2.【解答】解:(1)①如图:过点D作DH⊥x轴,
∵A(0,2),B(1,0),
∴OA=2,OB=1,
由旋转知,∠ABD=90°,AB=DB,
∴∠ABO+∠DBH=90°,
∵过点D作DH⊥x轴,
∴∠DBH+∠BDH=90°,
∴∠ABO=∠BDH,
在△AOB和△BHD中,
,
∴△AOB≌△BHD(AAS),
∴DH=OB=1,BH=OA=2,
∴OH=OB+BH=3
∴D(3,1);
(2)∵抛物线经过点O和D,
把D(3,1),O(0,0),代入得:
,
解得,
∴;
(3)在抛物线上存在点P,使得∠POB=∠BAO;理由如下:
设,
如图,当点P在x轴上方时,作PG⊥x轴于G,则OG=p,,
∵∠POB=∠BAO,
∴tan∠POB=tan∠BAO,
由①可得:OA=2,OB=1,
∵,,
∴,
解得:,
此时,即;
如图3,当点P在x轴上方时,作PI⊥x轴于I,则OI=p,,
∵∠POB=∠BAO,
∴tan∠POB=tan∠BAO,
∵,,
∴,
解得:,
此时,即;
综上所述,点P的坐标为或.
3.【解答】解:(1)∵点B(5,0),点C(4,3)都在抛物线y=﹣x2+bx+c上,
∴,
∴,
∴抛物线的解析式为y=﹣x2+6x﹣5.
(2)令y=0,则﹣x2+6x﹣5=0,
∴x=5或x=1,
∴A(1,0),
∴OA=1.
∵y=﹣x2+6x﹣5=﹣(x﹣3)2+4,
∴D(3,4).
过点D作DE⊥AB于点E,过点C作CF⊥AB于点F,CG⊥DE于点G,如图,
则OE=3,DE=4,OF=4,CF=3,
∴EF=OF﹣OE=4﹣3=1,AE=OE﹣OA=2,AF=OF﹣OA=3,
∴DE⊥AB,CF⊥AB,CG⊥DE,
∴四边形CGEF为矩形,
∴CG=EF=1,EG=CF=3,
∴DG=DE﹣EG=1,
∴AD2=AE2+DE2=22+42=20,
CD2=CG2+DG2=12+12=2,
AC2=AF2+CF2=32+32=18,
∴CD2+AC2=2+18=20,
∴CD2+AC2=AD2,
∴△ACD为直角三角形,
∴∠ACD=90°.
(3)①当点P在AC的上方时,如图,
设PC与AD交于点H,
由(2)知:∠ACD=90°,
∴∠PCA+∠PCD=90°,∠CAD+∠HDC=90°,
∵∠PCA=∠CAD,
∴∠HDC=∠PCD,
∴HD=HC.
∵∠PCA=∠CAD,
∴HA=HC,
∴HA=HD,
∵A(1,0),D(3,4),
∴H(2,2).
设直线CH的解析式为y=kx+a,
∴,
∴,
∴直线CH的解析式为yx+1,
令x=0,则y=1,
∴P(0,1);
②当点P在AC的下方时,如图,
∵∠PCA=∠CAD,
∴PC∥AD.
设直线AD的解析式为y=mx+n,
∵D(3,4),A(1,0),
∴,
∴,
∴直线AD的解析式为y=2x﹣2.
∴直线PC的解析式为y=2x+d,
∴2×4+d=3,
∴d=﹣5,
∴直线PC的解析式为y=2x﹣5,
令x=0,则y=﹣5,
∴P(0,﹣5).
综上,当∠PCA=∠CAD时,P点坐标为(0,1)或(0,﹣5).
4.【解答】解:(1)已知抛物线y=ax2+bx+c(a>0)与x轴左、右交点分别为A、B,与y轴负半轴交于点C,OB=OC=3OA,S△ABC=6,
∴AB=OA+OB=4OA,
∴,
解得:OA=1(负值舍去),
∴OB=3,OC=3,
∴A(﹣1,0),B(3,0),C(0,﹣3),
∴设抛物线的解析式为y=a(x+1)(x﹣3),把点C的坐标代入得:
﹣3=a(0+1)(0﹣3),
解得:a=1,
∴抛物线的解析式为y=x2﹣2x﹣3;
(2)①∵OB=OC,
∴∠OBC=∠OCB=45°,
∵∠OPC=45°=∠OBC,
∴当点P与点B重合时,满足题意;此时:P(3,0);
当点P与点B不重合时,则:O,C,B,P四点共圆,
∵∠BOC=90°,
∴BC为圆的直径,取BC的中点E,则点E即为圆心,连接EP,则:,
∵B(3,0),C(0,3),
∴,,,
设点P(m,m2﹣2m﹣3)(m>0),
则:,
整理得:m(m2﹣m﹣1)(m﹣3)=0,
解得:m=0(舍去)或m=3(舍去)或(舍去)或,
当时,,
∴;
综上所述,P(3,0)或;
②∵C(0.﹣3),D为OC的中点,
∴,
∵OA=1,
∴,
取点F(2,0),连接CF,则:OF=2,
∴,
∴∠OFC=∠OAD,
∵∠OPC=∠OAD,
∴∠OPC=∠OFC,
∴O,P,F,C四点共圆,
∵∠COF=90°,
∴CF为圆的直径,取CF的中点H,如图2,则,,
∵,
∴,
设P(n,n2﹣2n﹣3),
∴,
化简,得:n4﹣4n3+2n2+4n=n(n2﹣2n﹣2)(n﹣2)=0,
解得:n=0(舍去)或n=2或(舍去)或;
∴P(2,﹣3)或.
5.【解答】解:(1)将点A的坐标代入抛物线表达式得:0=9a,则a,
则抛物线的表达式为:y(x+1)2;
(2)令y(x+1)20,则x=﹣4或2,即点B(2,0),
则AB=2﹣(﹣4)=6;
(3)当点P在x轴下方时,
∵∠PBA=∠CAB,则PB∥AC,
由点A、C的坐标得,直线AC的表达式为:yx+2,
则直线PB的表达式为:y(x﹣2),
当点P在x轴上方时,
则PB的表达式为:y(x﹣2),
联立PB和抛物线的表达式得:(x﹣2)(x+1)2或(x﹣2)(x+1)2,
解得:x=2(舍去)或﹣2或﹣4.5,
则点P(﹣2,2)或(,).
6.【解答】解:(1)在y=﹣x2+3x+4中,
当x=0时,y=4,
∴点C(0,4),
当y=0时,﹣x2+3x+4=0,
解得:x1=﹣1,x2=4,
∴点A(﹣1,0),B(4,0);
(2)①由(1)知B(4,0),C(0,4),
设直线BC的解析式为y=kx+b(k≠0),
将点B(4,0),C(0,4)代入上式,得,
解得,
∴直线BC的解析式为y=﹣x+4,
∵C(0,4),
∴OC=4,
∵过P作y轴的平行线,交线段BC于点Q,如图,
可设P(m,﹣m2+3m+4),则Q(m,﹣m+4),
∴PQ=﹣m2+3m+4﹣(﹣m+4)=﹣m2+4m,
∵四边形OCPQ为平行四边形,
∴PQ=OC=4,
∴﹣m2+4m=4,
解得,m1=m2=2,
当m=2,得n=6,
∴P(2,6);
②解法一:作点C关于直线PQ的对称点D(2m,4),如图,
设直线PD的解析式为y=k1x+b1,
∵P(m,﹣m2+3m+4),
∴,
解得,
∴直线PD的解析式为y=(m﹣3)x﹣2m2+6m+4,
联立,
整理得,x2+(m﹣6)x﹣2m2+6m=0,
则Δ=(m﹣6)2﹣4×1×(﹣2m2+6m)
=9m2﹣36m+36
=9(m﹣2)2≥0,
解方程得x1=m,x2=6﹣2m,
∵,
∴x2=6﹣2m>x1,
∴当时,点P在运动过程中,抛物线上始终存在点E,使得∠EPQ=∠CPQ,
解法二:作点C关于直线PQ的对称点D(2m,4),
在y=﹣x2+3x+4中,
当x=2m时,y=﹣(2m)2+3×2m+4=﹣4m2+6m+4,
则,
∵,
∴y﹣4>0,
∴点D在抛物线内,
∴当时,点P在运动过程中,抛物线上始终存在点E,使得∠EPQ=∠CPQ.
7.【解答】解:(1)直线y=﹣x+3与x轴、y轴分别交于B、C两点,则点B、C的坐标分别为:(3,0)、(0,3),
由题意得:,
解得:,
则抛物线的表达式为:y=﹣x2+2x+3;
(2)∵S△MBC=S△OBC,
∴过点O作直线m∥BC交抛物线于点M,则点M为所求点,
由点B、C的坐标得,直线BC的表达式为:y=﹣x+3,
则直线m的表达式为:y=﹣x,
联立上式和抛物线的表达式得:﹣x=﹣x2+2x+3,则x,
即点M(,)或(,),
当M在BC上方时,
同理可得直线m的表达式为:y=﹣x+6,
联立上式和抛物线的表达式得:6﹣x=﹣x2+2x+3,此方程无解;
故点M(,)或(,);
(3)点D在抛物线上,则点D(2,3),连接CD,
过点D作DT⊥CB于点TA,交PB于点H,
∵∠PBC=∠DBC,
则点T是DH的中点,
由(1)知,BC的表达式为:y=﹣x+3,
则直线DT的表达式为:y=(x﹣2)+3=x+1,
联立上式和BC得表达式得:x+1=﹣x+3,则x=1,
即点T(1,2),
由中点坐标公式得,点H(0,1),
由点B、H的坐标得,直线BH的表达式为:yx+1,
联立上式和抛物线的表达式得:﹣x2+2x+3x+1,则x=3(舍去)或,
则点P(,).
8.【解答】解:(1)由题意得:y=a(x+1)(x﹣4)=a(x2﹣3x﹣4),
则﹣4a=3,则a,
则抛物线的表达式为:yx2x+3;
(2)过点C作CE∥AB,则∠ECB=∠CBA,
∵∠PCB=2∠CBA,则∠PCE=∠CBA,
则tan∠PCE=tan∠CAB,
则直线PC的表达式为:yx+3,
联立上式和抛物线的表达式得:x+3x2x+3,
解得:x=0(舍去)或2,
即点P(2,);
(3)过点P作PT⊥x轴于点T,交CB于点H,作DN⊥PH于点N,
则∠THP=∠CBA=α,tanα,则sinα,cosα,
由点B、C的坐标得,直线BC的表达式为:yx+3,
设点P(x,x2x+3),则点H(x,x+3),
则PH=(x2x+3)﹣(x+3)x2+3x,
则DH=PH sinαPH,BH(4﹣x),
则BD=HD+BHPH(4﹣x),
而PDPH sinαPH,
则PH(4﹣x)PH=PH(4﹣x)(x)2,
即的最大值为:.
9.【解答】解:(1)把C(0,3),D(4,﹣5)代入y=﹣x2+bx+c得:
,
解得,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)由C(0,3),D(4,﹣5)得直线CD解析式为y=﹣2x+3,
设P(m,﹣m2+2m+3),则E(m,﹣2m+3),
∵CO∥PE,
∴当CO=PE时,以P、E、O、C为顶点的四边形是平行四边形,
∴|﹣m2+2m+3+2m﹣3|=3,
∴m2﹣4m=3或m2﹣4m=﹣3,
解得m2或m2或m=1或m=3,
∴P的横坐标为2或2或1或3;
(3)抛物线上存在点Q,使∠QCD=45°,理由如下:
过D作DK⊥CQ于K,过K作TG∥y轴,过C作CT⊥TG于T,过D作DG⊥TG于G,
设K(p,q),
当CQ在CD右侧时,如图:
∵∠QCD=45°,
∴△CKD是等腰直角三角形,
∴CK=DK,∠CKD=90°,
∴∠CKT=90°﹣∠GKD=∠KDG,
∵∠T=∠G=90°,
∴△CTK≌△KGD(AAS),
∴CT=KG,TK=DG,
∵C(0,3),D(4,﹣5)
∴,
解得,
∴K(6,1),
由K(6,1),C(0,3)可得直线CK解析式为yx+3,
联立,
解得(此时C,Q重合,舍去)或,
∴Q(,);
当CQ在CD左侧时,如图:
同理可得K(﹣2,﹣3),直线CK解析式为y=3x+3,
联立,
解得或(舍去),
∴Q(﹣1,0);
综上所述,Q的坐标为(,)或(﹣1,0).
10.【解答】解:(1)抛物线y=﹣x2+bx+c经过A(4,0),C(﹣1,0)两点,将点A,点C的坐标代入得:
,
解得:,
∴抛物线的解析式为y=﹣x2+3x+4;
(2)设△APQ的面积为S1,△BCQ的面积为S2,S1﹣S2=5,
∴S△ACP﹣S△ABC=5.
抛物线y=﹣x2+3x+4与y轴交于点B,
当x=0时,y=4,
∴B(0,4).
∵A(4,0),C(﹣1,0),
∴OB=OA=4,AC=5,
∴,
∴S△ACP=15.
设P(t,﹣t2+3t+4),
∴,
∴t=1或t=2,
∴P(1,6)或P(2,6);
(3)过点P作PD⊥x轴于点D,如图,
∵OB=OA=4,
∴∠ABO=∠OAB=45°.
∵∠PAB+∠CBO=45°,
∴∠CBO+∠PAB+∠BAO=90°.
∵∠CBO+∠BCO=90°,
∴∠BCO=∠OAB+∠PAB=∠PAD.
∵∠BOC=∠PDA=90°,
∴△BOC∽△PDA,
∴.
设点P(a,﹣a2+3a+4),
∴PD=﹣a2+3a+4,AD=4﹣a,
∴,
整理得a2﹣7a+12=0,
解得a1=3或a2=4(不合题意,舍去),
∴P(3,4),
故答案为:(3,4).
11.【解答】解:(1)由抛物线的表达式知,点C(0,3),则OC=3,
∵tan∠CAO=3,则OA=1,即点A(﹣1,0),
将点A的坐标代入抛物线表达式得:0=﹣1﹣b+3,
则b=2,
则抛物线的表达式为:y=﹣x2+2x+3,
则点D(1,4);
(2)①由抛物线的表达式知,点B(3,0),
由点B、C的坐标知,直线BC的表达式为:y=﹣x+3,
设点P(m,﹣m2+2m+3),则点P关于x轴的对称点(m,m2﹣2m﹣3),
将点(m,m2﹣2m﹣3)的坐标代入y=﹣x+3得:m2﹣2m﹣3=﹣m+3,
解得:m=3(舍去)或﹣2,
即点P(﹣2,﹣5);
②设BM交抛物线对称轴于点H,过点H作HN⊥BD于点N,
由点B、P的坐标得,直线BP的表达式为:y=(x﹣3),即∠ABP=45°,
由点B、D的坐标得:tan∠NDH,
∵∠MBP=∠ABD,即∠DBM+∠MBA=∠MBA=∠ABP,
∴∠DBM=∠ABP=45°,
在△BDH中,tan∠NDH,∠DBH=45°,
故设NH=x=NB,则DN=2x,则DHx,
则BDBN+DN=3x,则x,
则DHx,则点H(1,);
由点B、H的坐标得,直线BH的表达式为:y(x﹣3),
联立上式和抛物线的表达式得:﹣x2+2x+3(x﹣3),
解得:x=3(舍去)或,
即点M(,).
12.【解答】解:(1)将点B的坐标代入上式得:0=9﹣3b﹣3,
解得:b=2,
则抛物线的表达式为:y=x2﹣2x﹣3;
(2)过点D作DH⊥OM于点H,过点H作GH平行于y轴交x轴于点G,交过点D和x轴的平行线于点T,
设点H(x,y),由抛物线的表达式知,点D(1,﹣4),
∵∠DOM=45°,则△ODH为等腰直角三角形,
则OH=DH,
∵∠OHG+∠DHT=90°,∠DHT+∠HDT=90°,
∴∠OHG=∠HDT,
在△HTD和△OGH中,
,
∴△HTD≌△OGH(AAS),
则OG=MT,DT=GH,
即x﹣y=4且x+y=1,
解得:x,y,即点H(,),
由点H的坐标得,直线OH的表达式为:yx,
联立上式和抛物线的表达式得:x=x2﹣2x﹣3,则x,
则点M(,);
当点M(M′)在第三象限时,
则OM⊥OM′,
则直线OM′的表达式为:yx,
联立上式和抛物线的表达式得:x=x2﹣2x﹣3,
解得:x,即M′(,),
综上,M(,)或(,);
(3)设点M(m,m2﹣2m﹣3),抛物线的对称轴为直线x=1,
由点A、M的坐标得,直线AM的表达式为:y=(m﹣3)(x+1),
则点E(1,2m﹣6),
同理可得,点F(1,﹣2m﹣2),
则HF﹣HE=2m+2﹣2m+6=8.
13.【解答】解:(1)由题意得:,解得:,
∴抛物线的函数表达式为yx2x+2;
设直线BC的函数表达式为y=mx+2,:
∴4m+2=0,
解得m,
∴直线BC的函数表达式为yx+2;
(2)过P作PH∥y轴交BC于H,如图:
设P(t,t2t+2),则H(t,t+2),
∴PHt2t+2﹣(t+2)t2+2t,
∴S△PBC=PH OB=(t2+2t)×4=﹣2t2+8t=﹣2(t﹣2)2+8,
∵﹣2<0,
∴当t=2时,S△PBC取最大值8,
此时P的坐标为(2,3);
(3)直线BP下方存在点Q,使得∠PBQ=45°,理由如下:
过P作PM⊥PB交BQ的延长线于M,过P作TK∥x轴,过B作BK⊥TK于K,过M作MT⊥TK于T,如图:
由(2)知P(2,3),
∵B(4,0),
∴PK=2,BK=3,
∵∠PBQ=45°,
∴△PBM是等腰直角三角形,
∴∠MPB=90°,PB=PM,
∴∠KPB=90°﹣∠TPM=∠TMP,
∵∠K=∠T=90°,
∴△BPK≌△PMT(AAS),
∴PK=MT=2,BK=PT=3,
∴M(﹣1,1),
设BM:y=mx+n,
则,解得:,
∴BM:yx,
解,得:或,
∴Q的坐标为(,).
14.【解答】解:(1)由题意得:y(x+1)(x﹣3)x2x+2;
(2)当x=0时,yx2x+2=2,
∴C(0,2),
由点B、C(0,2)的坐标得,直线BC为yx+2,
设点P(x,x2x+2),点D(x,x+2),
∴2PD+PE=2(x2x+2x﹣2)+xx2+5x,
当x时,2PD+PE有最大值,
此时点P(,);
(3)如图,以CB为对角线作正方形CTBK,
∴∠BCK=∠BCT=45°,
∴CK,CT与抛物线的另一个交点即为M,
如图,过T作x轴的平行线交y轴于Q,过B作BG⊥TQ于G,则OB=GQ=3,
∴∠CTB=90°=∠CQT=∠QGB,
∴∠QCT+∠CTQ=90°=∠CTQ+∠BTG,
∴∠QCT=∠BTG,
∵CT=BT,
∴△CQT≌△TGB(AAS),
∴QT=GB,CQ=TG,
设TQ=GB=m,则CQ=TG=3﹣m,
∴Q0=3﹣m﹣2=1﹣m,
∴T(m,m﹣1),
由TC=TB可得m2+(m﹣3)2=(m﹣3)2+(m﹣1)2,
解得m,
∴T(,),
则直线CT为y=﹣5x+2,
联立上式和抛物线的表达式得:﹣5x+2x2x+2,
解得:x=0(舍去)或,
即点M(,)、T(,)、C(0,2)、B(3,0),正方形CTBK,
则K(2.5,2.5);
同理可得直线CK为yx+2,
联立上式和抛物线的表达式得:x2x+2x+2,
解得:x或0(舍去),
则点M(,),
综上,点M的坐标M(,)或(,).
15.【解答】解:(1)在平面直角坐标系中,已知抛物线y=﹣x2+bx+c与x轴交于B(4,0)点,与y轴交于D(3,4),将点B,点D的坐标代入得:
,
解得:,
∴抛物线的解析式为y=﹣x2+3x+4;
(2)已知抛物线y=﹣x2+3x+4与y轴交于点C,
令x=0,得:y=4,
∴C(0,4),
∴OC=4,
∵OB=4,
∴OB=OC,
又∵∠BOC=90°,
∴∠OBC=∠OCB=45°,
设直线BC的解析式为y=kx+m,将点B,点C的坐标代入得:
,
解得:,
∴直线BC的解析式为y=﹣x+4;
作PH⊥BC交BC于点H,PM⊥x轴交x轴于点M,交BC于点N,如图1,
∵PM⊥x轴,
∴PM∥y轴,
∴∠PNH=∠OCB=45°,
∵PH⊥BC,
∴∠PHN=90°,
∴∠HPN=90°﹣∠PNH=45°,
∴∠HPN=∠PNH=45°,
∴△PHN是等腰直角三角形,
∴,
由题意得:,
∴,
设点P的坐标为(m,﹣m2+3m+4),则点N的坐标为(m,﹣m+4),
∴PN=﹣m2+3m+4﹣(﹣m+4)=﹣m2+4m=4,
解得:m=2,
∴﹣m2+3m+4=﹣22+3×2+4=6,
∴点P的坐标为(2,6);
(3)抛物线上存在点P,使∠CBP+∠ACO=45°;理由如下:
令y=0,则0=﹣x2+3x+4,
解得:x1=﹣1,x2=4,
∴A(﹣1,0),
如图2,将△AOC绕点O顺时针方向旋转90°至△A′OB,则A′O=AO=1,∠A′BO=∠ACO,
∴A′(0,1),
由(2)中的结论得,∠OBC=45°,
∵∠CBP+∠ACO=45°,
∴∠CBP=45°﹣∠ACO=∠OBC﹣∠A′BO=∠CBA′,
∴直线BA′上存在符合题意的点P,
设直线BA′的解析式为y=tx+n,将点B,点A′的坐标代入得:
,
解得:,
∴直线BA′的解析式为,
联立,
解得:或,
∴;
如图,连接CD、BD,过点B作BE⊥CD交于点E,
∵C(0,4),D(3,4),
∴CD∥x轴,
∵BE⊥CD,B(4,0),
∴∠E=90°,DE=4﹣3=1,BE=4,
∴CE=CD+DE=3+1=4,
∴CE=BE=4,
∴△CBE是等腰直角三角形,
∴∠CBE=45°,
∵AO=1,OC=4,
∴DE=AO,BE=OC,
又∵∠E=∠AOC=90°,
姑△BDE和△CAO中,
,
∴△BDE≌△CAO(SAS),
∴∠DBE=∠ACO,
∵∠CBP+∠ACO=45°,
∴∠CBP=45°﹣∠ACO=∠CBE﹣∠DBE=∠CBD,
∴直线BD上也存在符合题意的点P,
又∵点D(3,4)在抛物线上,
∴点P与点D重合,即P(3,4);
∴综上所述,抛物线上存在点P,使∠CBP+∠ACO=45°;点P的坐标为或(3,4).
16.【解答】解:(1)∵二次函数y=ax2+bx+4(a≠0)的图象经过点A(﹣4,0),B(1,0),
∴,
解得:,
∴该二次函数的表达式为y=﹣x2﹣3x+4;
(2)如图,设BP与y轴交于点E,
∵PD∥y轴,
∴∠DPB=∠OEB,
∵∠DPB=2∠BCO,
∴∠OEB=2∠BCO,
∴∠ECB=∠EBC,
∴BE=CE,
令x=0,得y=4,
∴C(0,4),OC=4,
设OE=a,则CE=4﹣a,
∴BE=4﹣a,
在Rt△BOE中,由勾股定理得:BE2=OE2+OB2,
∴(4﹣a)2=a2+12,
解得:a,
∴E(0,),
设BE所在直线表达式为y=kx+e(k≠0),
∴,
解得:,
∴直线BP的表达式为yx;
(3)有最大值.
如图,设PD与AC交于点N,
过点B作y轴的平行线与AC相交于点M,
设直线AC表达式为y=mx+n,
∵A(﹣4,0),C(0,4),
∴,
解得:,
∴直线AC表达式为y=x+4,
∴M点的坐标为(1,5),
∴BM=5,
∵BM∥PN,
∴△PNQ∽△BMQ,
∴,
设P(a0,﹣a02﹣3a0+4)(﹣4<a0<0),则N(a0,a0+4),
∴,
∴当a0=﹣2时,有最大值,
此时,点P的坐标为(﹣2,6).
17.【解答】解:(1)∵A(﹣1,0),B(4,0)是抛物线yx2+bx+c与x轴的两个交点,且二次项系数a,
∴根据抛物线的两点式知,y.
(2)根据抛物线表达式可求C(0,2),即OC=2.
∴2,
∵∠AOC=∠COB=90°,
∴△AOC∽△COB,
∴∠ACO=∠CBO,
∴∠QAB=∠QAC+∠CAO=∠CBA+45°+∠CAO=∠ACO+∠CAO+45°=135°,
∴∠BAP=180°﹣∠QAB=45°,
设P(m,n),且过点P作PD⊥x轴于D,则△ADP是等腰直角三角形,
∴AD=PD,即m+1=﹣n①,
又∵P在抛物线上,
∴②,
联立①②两式,解得m=6(﹣1舍去),此时n=﹣7,
∴点P的坐标是(6,﹣7).
(3)设PH与x轴的交点为Q1,P(a,),
则H(a,),PH,
若FP=FH,则∠FPH=∠FHP=∠BHQ1=∠BCO,
∴tan∠APQ1=tan∠BCO=2,
∴AQ1=2PQ1,
即a+1=2(),
解得a=3(﹣1舍去),此时PH.
若PF=PH,过点F作FM⊥y轴于点M,
∴∠PFH=∠PHF,
∵∠CFA=∠PFH,∠Q1HB=∠PHF,
∴∠CFA=∠Q1HB,
又∵∠ACF=∠BQ1H=90°,
∴△ACF∽△BQ1H,
∴CFAC,
在Rt△CMF中,MF=1,CM,
F(1,),
∴AF:,
将上式和抛物线解析式联立并解得x(﹣1舍去),
此时 PH.
若HF=HP,过点C作CE∥AB交AP于点E(见图),
∵∠CAF+∠CFA=90°,
∠PAQ+∠HPF=90°,
∠CFA=∠HFP=∠HPF,
∴∠CAF=∠PAQ1,
即 AP平分∠CAB,
∴CE=CA,
∴E(,2),
∴AE:,
联立抛物线解析式,解得x=5(﹣1舍去).
此时 PH.
∴当FP=FH时,PH;
当PF=PH时,PH;
当HF=HP时,PH;
18.【解答】解:(1)设抛物线的表达式为y=a(x﹣x1)(x﹣x2),
则y=a(x+2)(x﹣4)=ax2﹣2ax﹣8a,
即﹣8a=4,解得a,
故抛物线的表达式为yx2+x+4①;
(2)由点A、B的坐标知,OB=2OA,
故CO将△ABC的面积分成2:1两部分,此时,点P不在抛物线上;
如图1,当BHAB=2时,CH将△ABC的面积分成2:1两部分,
即点H的坐标为(2,0),
则CH和抛物线的交点即为点P,
由点C、H的坐标得,直线CH的表达式为y=﹣2x+4②,
联立①②并解得(不合题意的值已舍去),
故点P的坐标为(6,﹣8);
(3)在OB上取点E(2,0),则∠ACO=∠OCE,
∵∠OCA=∠OCB﹣∠OMA,故∠AMO=∠ECB,
过点E作EF⊥BC于点F,
在Rt△BOC中,由OB=OC知,∠OBC=45°,
则EFEB(4﹣2)BF,
由点B、C的坐标知,BC=4,
则CF=BC﹣BF=43,
则tan∠ECBtan∠AMO,
则tan∠AMO,
则OM=6,
故CM=OM±OC=6±4=2或10,
则t=2或10.
19.【解答】解:(1)令x=0,则y=4,
∴C(0,4);
令y=0,则x2x+4=0,
∴x=﹣2或x=3,
∴A(﹣2,0),B(3,0).
故答案为:(﹣2,0);(3,0);(0,4).
(2)①∵CP∥x轴,C(0,4),
∴P(1,4),
∴CP=1,AB=5,
∵CP∥x轴,
∴.
②如图,过点P作PQ∥AB交BC于点Q,
∴直线BC的解析式为:yx+4.
设点P的横坐标为m,
则P(m,m2m+4),Q(m2m,m2m+4).
∴PQ=m﹣(m2m)m2m,
∵PQ∥AB,
∴(m)2,
∴当m时,的最大值为.
另解:分别过点P,A作y轴的平行线,交直线BC于两点,仿照以上解法即可求解.
(3)假设存在点P使得∠BCO+2∠BCP=90°,即0<m<3.
过点C作CF∥x轴交抛物线于点F,
∵∠BCO+2∠PCB=90°,∠BCO+∠BCM+∠MCF=90°,
∴∠MCF=∠BCP,
延长CP交x轴于点M,
∵CF∥x轴,
∴∠PCF=∠BMC,
∴∠BCP=∠BMC,
∴△CBM为等腰三角形,
∵BC=5,
∴BM=5,OM=8,
∴M(8,0),
∴直线CM的解析式为:yx+4,
令x2x+4x+4,
解得x或x=0(舍),
∴存在点P满足题意,此时m.
20.【解答】解:(1)设抛物线的表达式为y=a(x﹣2)2﹣4,
将O(0,0)代入得:4a﹣4=0,
解得a=1,
∴y=(x﹣2)2﹣4=x2﹣4x;
(2)过A作AT⊥y轴于T,过P作PK⊥x轴于K,如图:
设P(m,m2﹣4m),
在y=x2﹣4x中,令y=0得x=0或x=4,
∴B(4,0);
∵∠AOB+∠AOT=90°,∠AOB+∠PBO=90°,
∴∠AOT=∠PBO,
∵∠ATO=90°=∠PKB,
∴△AOT∽△PBK,
∴,
∵A(2,﹣4),
∴,
解得m或m=4(此时P与B重合,舍去),
∴P(,).
21.【解答】解:(1)设抛物线的表达式为:y=a(x+3)(x﹣4)=a(x2﹣x﹣12),
即﹣12a=4,则a,
故抛物线的表达式为:yx2x+4①;
(2)在Rt△AOC中,tan∠CAO,
∵∠CAO+∠ABP=90°,
则tan∠ABP,
故设直线BP的表达式为:y(x﹣4)②,
联立①②得:x2x+4(x﹣4),
解得:xx0(不合题意的值已舍去);
(3)作∠EAG=∠BCD,
设AG=2BC=2×48,
∵AE=2CD,
∴△BCD∽△GAE且相似比为1:2,
则EG=2BD,
故当C、E、G共线时,CE+2BD=CE+EG=CG为最小,
在△ABC中,设AC边上的高为h,
则S△ABCAC hAB×CO,
即5h=4×7,
解得:h,
则sin∠ACBsin∠EAG,
则tan∠EAG=7,
过点G作GN⊥x轴于点N,
则NG=AG sin∠EAG,
即点G的纵坐标为:,
同理可得,点G的横坐标为:,
即点G(,),
由点C、G的坐标得,CG,
即CE+2BD的最小值为.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺练习二次函数中的角度问题
1.如图,抛物线与y=ax2+bx+3与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C.顶点为(1,4).直线y=3x+7与x,y轴分别相交于点D,E,与直线BC相交于点F.
(1)求该抛物线对应的函数表达式;
(2)请探究在第三象限内的抛物线上是否存在点P,使得∠PBF=∠DFB?若存在,求出点P的坐标;若不存在,说明理由.
2.已知在平面直角坐标系xOy中,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上.现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线经过点O和D.
(1)求点D的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否存在点P,使得∠POB=∠BAO?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.
3.已知点B(5,0),点C(4,3)都在抛物线y=﹣x2+bx+c上,其中点A是抛物线与x轴的交点,点D是抛物线的顶点,连接AD,CD.
(1)求抛物线的解析式;
(2)求∠ACD的度数;
(3)点P是y轴上的一个动点,当∠PCA=∠CAD时,直接写出P点坐标.
4.已知抛物线y=ax2+bx+c(a>0)与x轴左、右交点分别为A、B,与y轴负半轴交于点C,坐标原点为O,若OB=OC=3OA,S△ABC=6,点P是抛物线上的动点(点P在y轴右侧).
(1)求抛物线的解析式;
(2)D是线段OC的中点,
①当∠OPC=45°时,请求出点P的坐标;
②当∠OPC=∠OAD时,请求出点P的坐标.
5.如图,在平面直角坐标系中,抛物线y=a(x+1)2(a≠0)与x轴交于点A(﹣4,0)和点B,连结AC.
(1)求抛物线的解析式;
(2)求线段AB的长度;
(3)点P是抛物线上的一个动点,满足∠PBA=∠CAB,求点P的坐标.
6.如图,已知抛物线y=﹣x2+3x+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)点P(m,n)是线段BC上方抛物线上的一动点,过P作y轴的平行线,交线段BC于点Q.
①当四边形OCPQ为平行四边形时,求点P的坐标;
②当时,在点P运动过程中,抛物线上是否始终存在点E,使得∠EPQ=∠CPQ,请说明理由.
7.如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,抛物线y=﹣x2+bx+c经过点B、C,与x轴另一交点为A.
(1)求抛物线的解析式;
(2)若点M是抛物线上的一点,使得S△MBC=S△OBC,请求出点M的坐标;
(3)点D(2,m)在第一象限的抛物线上,连接BD.在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P的坐标;如果不存在,请说明理由.
8.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3与x轴分别交于点A(﹣1,0)、点B(4,0),与y轴交于点C.点P是第一象限的抛物线上一动点.
(1)求抛物线的表达式;
(2)如图,连接PC,当∠PCB=2∠CBA时,求点P的坐标;
(3)如图,过点P作PD⊥BC于点D,求的最大值.
9.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C(0,3),且经过点D(4,﹣5).
(1)求抛物线的解析式;
(2)点P在抛物线上,过P作PE∥y轴,交直线CD于点E,若以P、E、O、C为顶点的四边形是平行四边形,求点P的横坐标;
(3)抛物线上是否存在点Q,使∠QCD=45°.若存在,请直接写出点Q的坐标;若不存在,请说明理由.
10.如图,抛物线y=﹣x2+bx+c经过A(4,0),C(﹣1,0)两点,与y轴交于点B,P为第一象限抛物线上的动点,连接AB、BC、PA、PC,PC与AB相交于点Q.
(1)求抛物线的解析式;
(2)设△APQ的面积为S1,△BCQ的面积为S2,当S1﹣S2=5时,求点P的坐标;
(3)抛物线上存在点P,满足∠PAB+∠CBO=45°,则点P的坐标为 .
11.如图,在平面直角坐标系xOy中,已知抛物线y=﹣x2+bx+3与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,联结AC,tan∠CAO=3,抛物线的顶点为点D.
(1)求b的值和点D的坐标;
(2)点P是抛物线上一点(不与点B重合),点P关于x轴的对称点恰好在直线BC上.
①求点P的坐标;
②点M是抛物线上一点且在对称轴左侧,联结BM,如果∠MBP=∠ABD,求点M的坐标.
12.已知:抛物线y=x2﹣bx﹣3交x、y轴于A、B(3,0),交y轴于C,顶点为D,M为抛物线上动点.
(1)求抛物线的解析式;
(2)在M运动过程中,连OM,当∠DOM=45°时,求M点坐标;
(3)随着M运动到第一象限,如图(2)直线AM交对称轴于E,直线MB交对称轴于F,若对称轴交x轴于H,求HF﹣HE的值.
13.如图,在平面直角坐标系中,抛物线与x轴交于点A,B,其中点B的坐标为(4,0),与y轴交于点C(0,2).
(1)求抛物线和直线BC的函数表达式;
(2)点P是直线BC上方的抛物线上一个动点,当△PBC面积最大时,求P点的坐标;
(3)连接B和(2)中求出的点P,点Q位于直线BP下方且在抛物线上,若∠PBQ=45°,求点Q的坐标.
14.如图,抛物线yx2+bx+c与x轴交于A,B两点,与y轴交于点C,点A坐标为(﹣1,0),点B坐标为(3,0).
(1)求此抛物线的函数解析式.
(2)点P是直线BC上方抛物线上一个动点,过点P作x轴的垂线交直线BC于点D,过点P作y轴的垂线,垂足为点E,求2PD+PE的最大值,及此时P点的坐标.
(3)点M为该抛物线上的点,当∠MCB=45°时,请直接写出满足条件的点M的坐标.
15.如图,在平面直角坐标系中,已知抛物线y=﹣x2+bx+c与x轴交于A,B(4,0)两点,与y轴交于点C,点D(3,4)在抛物线上,点P是抛物线上一动点.
(1)求该抛物线的解析式;
(2)连接BC,若BC上方抛物线上有一点P,且P到直线BC的距离为,求点P的坐标;
(3)如图,连接AC,BC,抛物线上是否存在点P,使∠CBP+∠ACO=45°?若存在,请直接写出点P的坐标;若不存在,请说明理由.
16.二次函数y=ax2+bx+4(a≠0)的图象经过点A(﹣4,0),B(1,0),与y轴交于点C,点P为第二象限内抛物线上一点,连接BP、AC,交于点Q,过点P作PD⊥x轴于点D.
(1)求二次函数的表达式;
(2)连接BC,当∠DPB=2∠BCO时,求直线BP的表达式;
(3)请判断:是否有最大值,如有请求出有最大值时点P的坐标,如没有请说明理由.
17.如图,抛物线yx2+bx+c与x轴交于A(﹣1,0),B(4,0),与y轴交于点C.连接AC,BC,点P在抛物线上运动.
(1)求抛物线的表达式;
(2)如图①,若点P在第四象限,点Q在PA的延长线上,当∠CAQ=∠CBA+45°时,求点P的坐标;
(3)如图②,若点P在第一象限,直线AP交BC于点F,过点P作x轴的垂线交BC于点H,当△PFH为等腰三角形时,求线段PH的长.
18.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+4(a≠0)经过点A(﹣2,0)和点B(4,0).
(1)求这条抛物线所对应的函数表达式;
(2)点P为该抛物线上一点(不与点C重合),直线CP将△ABC的面积分成2:1两部分,求点P的坐标;
(3)点M从点C出发,以每秒1个单位的速度沿y轴移动,运动时间为t秒,当∠OCA=∠OCB﹣∠OMA时,求t的值.
19.如图,抛物线yx2x+4与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.
(1)A,B,C三点的坐标为 , , .
(2)连接AP,交线段BC于点D,
①当CP与x轴平行时,求的值;
②当CP与x轴不平行时,求的最大值;
(3)连接CP,是否存在点P,使得∠BCO+2∠PCB=90°,若存在,求m的值,若不存在,请说明理由.
20.如图,抛物线y=ax2+bx+c(a≠0)经过坐标原点O,且顶点为A(2,﹣4).
(1)求抛物线的表达式;
(2)设抛物线与x轴正半轴的交点为B,点P位于抛物线上且在x轴下方,连接OA、PB,若∠AOB+∠PBO=90°,求点P的坐标.
21.如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于两点A(﹣3,0),B(4,0),与y轴交于点C(0,4).
(1)求此抛物线的解析式;
(2)已知抛物线上有一点P(x0,y0),其中y0<0,若∠CAO+∠ABP=90°,求x0的值;
(3)若点D,E分别是线段AC,AB上的动点,且AE=2CD,求CE+2BD的最小值.
参考答案
1.【解答】解:(1)∵抛物线与y=ax2+bx+3的顶点为(1,4),
∴y=ax2+bx+3=a(x﹣1)2+4,
由题意得:,
解得:,
∴抛物线的表达式为y=﹣x2+2x+3;
(2)在第三象限内的抛物线上存在点P,使得∠PBF=∠DFB;理由如下:
∵直线y=3x+7与x,y轴分别相交于点D,E,
∴当y=0时,3x+7=0,
解得,
∴点D的坐标为.
抛物线与y=﹣x2+2x+3与x轴相交于A,B两点(点A在点B的左侧),
当y=0时得:﹣x2+2x+3=0,
解得x1=﹣1,x2=3,
∴点A的坐标为(﹣1,0),点B的坐标为(3,0),
在y=﹣x2+2x+3中,当x=0时,y=3,
∴点C的坐标为(0,3),
设直线BC的解析式为y=sx+t,将点B,点C的坐标代入得:
,
解得:,
∴直线BC的表达式为y=﹣x+3,
联立得:,
解得,
∴点F的坐标为(﹣1,4).
连接FA,过点P作PM⊥x轴,垂足为M,
由题知FA⊥x轴,,AF=4,,
设点P的坐标为(m,﹣m2+2m+3),
,
当∠PBF=∠DFB时,,
解得,m2=3(舍去),
点P的坐标为.
2.【解答】解:(1)①如图:过点D作DH⊥x轴,
∵A(0,2),B(1,0),
∴OA=2,OB=1,
由旋转知,∠ABD=90°,AB=DB,
∴∠ABO+∠DBH=90°,
∵过点D作DH⊥x轴,
∴∠DBH+∠BDH=90°,
∴∠ABO=∠BDH,
在△AOB和△BHD中,
,
∴△AOB≌△BHD(AAS),
∴DH=OB=1,BH=OA=2,
∴OH=OB+BH=3
∴D(3,1);
(2)∵抛物线经过点O和D,
把D(3,1),O(0,0),代入得:
,
解得,
∴;
(3)在抛物线上存在点P,使得∠POB=∠BAO;理由如下:
设,
如图,当点P在x轴上方时,作PG⊥x轴于G,则OG=p,,
∵∠POB=∠BAO,
∴tan∠POB=tan∠BAO,
由①可得:OA=2,OB=1,
∵,,
∴,
解得:,
此时,即;
如图3,当点P在x轴上方时,作PI⊥x轴于I,则OI=p,,
∵∠POB=∠BAO,
∴tan∠POB=tan∠BAO,
∵,,
∴,
解得:,
此时,即;
综上所述,点P的坐标为或.
3.【解答】解:(1)∵点B(5,0),点C(4,3)都在抛物线y=﹣x2+bx+c上,
∴,
∴,
∴抛物线的解析式为y=﹣x2+6x﹣5.
(2)令y=0,则﹣x2+6x﹣5=0,
∴x=5或x=1,
∴A(1,0),
∴OA=1.
∵y=﹣x2+6x﹣5=﹣(x﹣3)2+4,
∴D(3,4).
过点D作DE⊥AB于点E,过点C作CF⊥AB于点F,CG⊥DE于点G,如图,
则OE=3,DE=4,OF=4,CF=3,
∴EF=OF﹣OE=4﹣3=1,AE=OE﹣OA=2,AF=OF﹣OA=3,
∴DE⊥AB,CF⊥AB,CG⊥DE,
∴四边形CGEF为矩形,
∴CG=EF=1,EG=CF=3,
∴DG=DE﹣EG=1,
∴AD2=AE2+DE2=22+42=20,
CD2=CG2+DG2=12+12=2,
AC2=AF2+CF2=32+32=18,
∴CD2+AC2=2+18=20,
∴CD2+AC2=AD2,
∴△ACD为直角三角形,
∴∠ACD=90°.
(3)①当点P在AC的上方时,如图,
设PC与AD交于点H,
由(2)知:∠ACD=90°,
∴∠PCA+∠PCD=90°,∠CAD+∠HDC=90°,
∵∠PCA=∠CAD,
∴∠HDC=∠PCD,
∴HD=HC.
∵∠PCA=∠CAD,
∴HA=HC,
∴HA=HD,
∵A(1,0),D(3,4),
∴H(2,2).
设直线CH的解析式为y=kx+a,
∴,
∴,
∴直线CH的解析式为yx+1,
令x=0,则y=1,
∴P(0,1);
②当点P在AC的下方时,如图,
∵∠PCA=∠CAD,
∴PC∥AD.
设直线AD的解析式为y=mx+n,
∵D(3,4),A(1,0),
∴,
∴,
∴直线AD的解析式为y=2x﹣2.
∴直线PC的解析式为y=2x+d,
∴2×4+d=3,
∴d=﹣5,
∴直线PC的解析式为y=2x﹣5,
令x=0,则y=﹣5,
∴P(0,﹣5).
综上,当∠PCA=∠CAD时,P点坐标为(0,1)或(0,﹣5).
4.【解答】解:(1)已知抛物线y=ax2+bx+c(a>0)与x轴左、右交点分别为A、B,与y轴负半轴交于点C,OB=OC=3OA,S△ABC=6,
∴AB=OA+OB=4OA,
∴,
解得:OA=1(负值舍去),
∴OB=3,OC=3,
∴A(﹣1,0),B(3,0),C(0,﹣3),
∴设抛物线的解析式为y=a(x+1)(x﹣3),把点C的坐标代入得:
﹣3=a(0+1)(0﹣3),
解得:a=1,
∴抛物线的解析式为y=x2﹣2x﹣3;
(2)①∵OB=OC,
∴∠OBC=∠OCB=45°,
∵∠OPC=45°=∠OBC,
∴当点P与点B重合时,满足题意;此时:P(3,0);
当点P与点B不重合时,则:O,C,B,P四点共圆,
∵∠BOC=90°,
∴BC为圆的直径,取BC的中点E,则点E即为圆心,连接EP,则:,
∵B(3,0),C(0,3),
∴,,,
设点P(m,m2﹣2m﹣3)(m>0),
则:,
整理得:m(m2﹣m﹣1)(m﹣3)=0,
解得:m=0(舍去)或m=3(舍去)或(舍去)或,
当时,,
∴;
综上所述,P(3,0)或;
②∵C(0.﹣3),D为OC的中点,
∴,
∵OA=1,
∴,
取点F(2,0),连接CF,则:OF=2,
∴,
∴∠OFC=∠OAD,
∵∠OPC=∠OAD,
∴∠OPC=∠OFC,
∴O,P,F,C四点共圆,
∵∠COF=90°,
∴CF为圆的直径,取CF的中点H,如图2,则,,
∵,
∴,
设P(n,n2﹣2n﹣3),
∴,
化简,得:n4﹣4n3+2n2+4n=n(n2﹣2n﹣2)(n﹣2)=0,
解得:n=0(舍去)或n=2或(舍去)或;
∴P(2,﹣3)或.
5.【解答】解:(1)将点A的坐标代入抛物线表达式得:0=9a,则a,
则抛物线的表达式为:y(x+1)2;
(2)令y(x+1)20,则x=﹣4或2,即点B(2,0),
则AB=2﹣(﹣4)=6;
(3)当点P在x轴下方时,
∵∠PBA=∠CAB,则PB∥AC,
由点A、C的坐标得,直线AC的表达式为:yx+2,
则直线PB的表达式为:y(x﹣2),
当点P在x轴上方时,
则PB的表达式为:y(x﹣2),
联立PB和抛物线的表达式得:(x﹣2)(x+1)2或(x﹣2)(x+1)2,
解得:x=2(舍去)或﹣2或﹣4.5,
则点P(﹣2,2)或(,).
6.【解答】解:(1)在y=﹣x2+3x+4中,
当x=0时,y=4,
∴点C(0,4),
当y=0时,﹣x2+3x+4=0,
解得:x1=﹣1,x2=4,
∴点A(﹣1,0),B(4,0);
(2)①由(1)知B(4,0),C(0,4),
设直线BC的解析式为y=kx+b(k≠0),
将点B(4,0),C(0,4)代入上式,得,
解得,
∴直线BC的解析式为y=﹣x+4,
∵C(0,4),
∴OC=4,
∵过P作y轴的平行线,交线段BC于点Q,如图,
可设P(m,﹣m2+3m+4),则Q(m,﹣m+4),
∴PQ=﹣m2+3m+4﹣(﹣m+4)=﹣m2+4m,
∵四边形OCPQ为平行四边形,
∴PQ=OC=4,
∴﹣m2+4m=4,
解得,m1=m2=2,
当m=2,得n=6,
∴P(2,6);
②解法一:作点C关于直线PQ的对称点D(2m,4),如图,
设直线PD的解析式为y=k1x+b1,
∵P(m,﹣m2+3m+4),
∴,
解得,
∴直线PD的解析式为y=(m﹣3)x﹣2m2+6m+4,
联立,
整理得,x2+(m﹣6)x﹣2m2+6m=0,
则Δ=(m﹣6)2﹣4×1×(﹣2m2+6m)
=9m2﹣36m+36
=9(m﹣2)2≥0,
解方程得x1=m,x2=6﹣2m,
∵,
∴x2=6﹣2m>x1,
∴当时,点P在运动过程中,抛物线上始终存在点E,使得∠EPQ=∠CPQ,
解法二:作点C关于直线PQ的对称点D(2m,4),
在y=﹣x2+3x+4中,
当x=2m时,y=﹣(2m)2+3×2m+4=﹣4m2+6m+4,
则,
∵,
∴y﹣4>0,
∴点D在抛物线内,
∴当时,点P在运动过程中,抛物线上始终存在点E,使得∠EPQ=∠CPQ.
7.【解答】解:(1)直线y=﹣x+3与x轴、y轴分别交于B、C两点,则点B、C的坐标分别为:(3,0)、(0,3),
由题意得:,
解得:,
则抛物线的表达式为:y=﹣x2+2x+3;
(2)∵S△MBC=S△OBC,
∴过点O作直线m∥BC交抛物线于点M,则点M为所求点,
由点B、C的坐标得,直线BC的表达式为:y=﹣x+3,
则直线m的表达式为:y=﹣x,
联立上式和抛物线的表达式得:﹣x=﹣x2+2x+3,则x,
即点M(,)或(,),
当M在BC上方时,
同理可得直线m的表达式为:y=﹣x+6,
联立上式和抛物线的表达式得:6﹣x=﹣x2+2x+3,此方程无解;
故点M(,)或(,);
(3)点D在抛物线上,则点D(2,3),连接CD,
过点D作DT⊥CB于点TA,交PB于点H,
∵∠PBC=∠DBC,
则点T是DH的中点,
由(1)知,BC的表达式为:y=﹣x+3,
则直线DT的表达式为:y=(x﹣2)+3=x+1,
联立上式和BC得表达式得:x+1=﹣x+3,则x=1,
即点T(1,2),
由中点坐标公式得,点H(0,1),
由点B、H的坐标得,直线BH的表达式为:yx+1,
联立上式和抛物线的表达式得:﹣x2+2x+3x+1,则x=3(舍去)或,
则点P(,).
8.【解答】解:(1)由题意得:y=a(x+1)(x﹣4)=a(x2﹣3x﹣4),
则﹣4a=3,则a,
则抛物线的表达式为:yx2x+3;
(2)过点C作CE∥AB,则∠ECB=∠CBA,
∵∠PCB=2∠CBA,则∠PCE=∠CBA,
则tan∠PCE=tan∠CAB,
则直线PC的表达式为:yx+3,
联立上式和抛物线的表达式得:x+3x2x+3,
解得:x=0(舍去)或2,
即点P(2,);
(3)过点P作PT⊥x轴于点T,交CB于点H,作DN⊥PH于点N,
则∠THP=∠CBA=α,tanα,则sinα,cosα,
由点B、C的坐标得,直线BC的表达式为:yx+3,
设点P(x,x2x+3),则点H(x,x+3),
则PH=(x2x+3)﹣(x+3)x2+3x,
则DH=PH sinαPH,BH(4﹣x),
则BD=HD+BHPH(4﹣x),
而PDPH sinαPH,
则PH(4﹣x)PH=PH(4﹣x)(x)2,
即的最大值为:.
9.【解答】解:(1)把C(0,3),D(4,﹣5)代入y=﹣x2+bx+c得:
,
解得,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)由C(0,3),D(4,﹣5)得直线CD解析式为y=﹣2x+3,
设P(m,﹣m2+2m+3),则E(m,﹣2m+3),
∵CO∥PE,
∴当CO=PE时,以P、E、O、C为顶点的四边形是平行四边形,
∴|﹣m2+2m+3+2m﹣3|=3,
∴m2﹣4m=3或m2﹣4m=﹣3,
解得m2或m2或m=1或m=3,
∴P的横坐标为2或2或1或3;
(3)抛物线上存在点Q,使∠QCD=45°,理由如下:
过D作DK⊥CQ于K,过K作TG∥y轴,过C作CT⊥TG于T,过D作DG⊥TG于G,
设K(p,q),
当CQ在CD右侧时,如图:
∵∠QCD=45°,
∴△CKD是等腰直角三角形,
∴CK=DK,∠CKD=90°,
∴∠CKT=90°﹣∠GKD=∠KDG,
∵∠T=∠G=90°,
∴△CTK≌△KGD(AAS),
∴CT=KG,TK=DG,
∵C(0,3),D(4,﹣5)
∴,
解得,
∴K(6,1),
由K(6,1),C(0,3)可得直线CK解析式为yx+3,
联立,
解得(此时C,Q重合,舍去)或,
∴Q(,);
当CQ在CD左侧时,如图:
同理可得K(﹣2,﹣3),直线CK解析式为y=3x+3,
联立,
解得或(舍去),
∴Q(﹣1,0);
综上所述,Q的坐标为(,)或(﹣1,0).
10.【解答】解:(1)抛物线y=﹣x2+bx+c经过A(4,0),C(﹣1,0)两点,将点A,点C的坐标代入得:
,
解得:,
∴抛物线的解析式为y=﹣x2+3x+4;
(2)设△APQ的面积为S1,△BCQ的面积为S2,S1﹣S2=5,
∴S△ACP﹣S△ABC=5.
抛物线y=﹣x2+3x+4与y轴交于点B,
当x=0时,y=4,
∴B(0,4).
∵A(4,0),C(﹣1,0),
∴OB=OA=4,AC=5,
∴,
∴S△ACP=15.
设P(t,﹣t2+3t+4),
∴,
∴t=1或t=2,
∴P(1,6)或P(2,6);
(3)过点P作PD⊥x轴于点D,如图,
∵OB=OA=4,
∴∠ABO=∠OAB=45°.
∵∠PAB+∠CBO=45°,
∴∠CBO+∠PAB+∠BAO=90°.
∵∠CBO+∠BCO=90°,
∴∠BCO=∠OAB+∠PAB=∠PAD.
∵∠BOC=∠PDA=90°,
∴△BOC∽△PDA,
∴.
设点P(a,﹣a2+3a+4),
∴PD=﹣a2+3a+4,AD=4﹣a,
∴,
整理得a2﹣7a+12=0,
解得a1=3或a2=4(不合题意,舍去),
∴P(3,4),
故答案为:(3,4).
11.【解答】解:(1)由抛物线的表达式知,点C(0,3),则OC=3,
∵tan∠CAO=3,则OA=1,即点A(﹣1,0),
将点A的坐标代入抛物线表达式得:0=﹣1﹣b+3,
则b=2,
则抛物线的表达式为:y=﹣x2+2x+3,
则点D(1,4);
(2)①由抛物线的表达式知,点B(3,0),
由点B、C的坐标知,直线BC的表达式为:y=﹣x+3,
设点P(m,﹣m2+2m+3),则点P关于x轴的对称点(m,m2﹣2m﹣3),
将点(m,m2﹣2m﹣3)的坐标代入y=﹣x+3得:m2﹣2m﹣3=﹣m+3,
解得:m=3(舍去)或﹣2,
即点P(﹣2,﹣5);
②设BM交抛物线对称轴于点H,过点H作HN⊥BD于点N,
由点B、P的坐标得,直线BP的表达式为:y=(x﹣3),即∠ABP=45°,
由点B、D的坐标得:tan∠NDH,
∵∠MBP=∠ABD,即∠DBM+∠MBA=∠MBA=∠ABP,
∴∠DBM=∠ABP=45°,
在△BDH中,tan∠NDH,∠DBH=45°,
故设NH=x=NB,则DN=2x,则DHx,
则BDBN+DN=3x,则x,
则DHx,则点H(1,);
由点B、H的坐标得,直线BH的表达式为:y(x﹣3),
联立上式和抛物线的表达式得:﹣x2+2x+3(x﹣3),
解得:x=3(舍去)或,
即点M(,).
12.【解答】解:(1)将点B的坐标代入上式得:0=9﹣3b﹣3,
解得:b=2,
则抛物线的表达式为:y=x2﹣2x﹣3;
(2)过点D作DH⊥OM于点H,过点H作GH平行于y轴交x轴于点G,交过点D和x轴的平行线于点T,
设点H(x,y),由抛物线的表达式知,点D(1,﹣4),
∵∠DOM=45°,则△ODH为等腰直角三角形,
则OH=DH,
∵∠OHG+∠DHT=90°,∠DHT+∠HDT=90°,
∴∠OHG=∠HDT,
在△HTD和△OGH中,
,
∴△HTD≌△OGH(AAS),
则OG=MT,DT=GH,
即x﹣y=4且x+y=1,
解得:x,y,即点H(,),
由点H的坐标得,直线OH的表达式为:yx,
联立上式和抛物线的表达式得:x=x2﹣2x﹣3,则x,
则点M(,);
当点M(M′)在第三象限时,
则OM⊥OM′,
则直线OM′的表达式为:yx,
联立上式和抛物线的表达式得:x=x2﹣2x﹣3,
解得:x,即M′(,),
综上,M(,)或(,);
(3)设点M(m,m2﹣2m﹣3),抛物线的对称轴为直线x=1,
由点A、M的坐标得,直线AM的表达式为:y=(m﹣3)(x+1),
则点E(1,2m﹣6),
同理可得,点F(1,﹣2m﹣2),
则HF﹣HE=2m+2﹣2m+6=8.
13.【解答】解:(1)由题意得:,解得:,
∴抛物线的函数表达式为yx2x+2;
设直线BC的函数表达式为y=mx+2,:
∴4m+2=0,
解得m,
∴直线BC的函数表达式为yx+2;
(2)过P作PH∥y轴交BC于H,如图:
设P(t,t2t+2),则H(t,t+2),
∴PHt2t+2﹣(t+2)t2+2t,
∴S△PBC=PH OB=(t2+2t)×4=﹣2t2+8t=﹣2(t﹣2)2+8,
∵﹣2<0,
∴当t=2时,S△PBC取最大值8,
此时P的坐标为(2,3);
(3)直线BP下方存在点Q,使得∠PBQ=45°,理由如下:
过P作PM⊥PB交BQ的延长线于M,过P作TK∥x轴,过B作BK⊥TK于K,过M作MT⊥TK于T,如图:
由(2)知P(2,3),
∵B(4,0),
∴PK=2,BK=3,
∵∠PBQ=45°,
∴△PBM是等腰直角三角形,
∴∠MPB=90°,PB=PM,
∴∠KPB=90°﹣∠TPM=∠TMP,
∵∠K=∠T=90°,
∴△BPK≌△PMT(AAS),
∴PK=MT=2,BK=PT=3,
∴M(﹣1,1),
设BM:y=mx+n,
则,解得:,
∴BM:yx,
解,得:或,
∴Q的坐标为(,).
14.【解答】解:(1)由题意得:y(x+1)(x﹣3)x2x+2;
(2)当x=0时,yx2x+2=2,
∴C(0,2),
由点B、C(0,2)的坐标得,直线BC为yx+2,
设点P(x,x2x+2),点D(x,x+2),
∴2PD+PE=2(x2x+2x﹣2)+xx2+5x,
当x时,2PD+PE有最大值,
此时点P(,);
(3)如图,以CB为对角线作正方形CTBK,
∴∠BCK=∠BCT=45°,
∴CK,CT与抛物线的另一个交点即为M,
如图,过T作x轴的平行线交y轴于Q,过B作BG⊥TQ于G,则OB=GQ=3,
∴∠CTB=90°=∠CQT=∠QGB,
∴∠QCT+∠CTQ=90°=∠CTQ+∠BTG,
∴∠QCT=∠BTG,
∵CT=BT,
∴△CQT≌△TGB(AAS),
∴QT=GB,CQ=TG,
设TQ=GB=m,则CQ=TG=3﹣m,
∴Q0=3﹣m﹣2=1﹣m,
∴T(m,m﹣1),
由TC=TB可得m2+(m﹣3)2=(m﹣3)2+(m﹣1)2,
解得m,
∴T(,),
则直线CT为y=﹣5x+2,
联立上式和抛物线的表达式得:﹣5x+2x2x+2,
解得:x=0(舍去)或,
即点M(,)、T(,)、C(0,2)、B(3,0),正方形CTBK,
则K(2.5,2.5);
同理可得直线CK为yx+2,
联立上式和抛物线的表达式得:x2x+2x+2,
解得:x或0(舍去),
则点M(,),
综上,点M的坐标M(,)或(,).
15.【解答】解:(1)在平面直角坐标系中,已知抛物线y=﹣x2+bx+c与x轴交于B(4,0)点,与y轴交于D(3,4),将点B,点D的坐标代入得:
,
解得:,
∴抛物线的解析式为y=﹣x2+3x+4;
(2)已知抛物线y=﹣x2+3x+4与y轴交于点C,
令x=0,得:y=4,
∴C(0,4),
∴OC=4,
∵OB=4,
∴OB=OC,
又∵∠BOC=90°,
∴∠OBC=∠OCB=45°,
设直线BC的解析式为y=kx+m,将点B,点C的坐标代入得:
,
解得:,
∴直线BC的解析式为y=﹣x+4;
作PH⊥BC交BC于点H,PM⊥x轴交x轴于点M,交BC于点N,如图1,
∵PM⊥x轴,
∴PM∥y轴,
∴∠PNH=∠OCB=45°,
∵PH⊥BC,
∴∠PHN=90°,
∴∠HPN=90°﹣∠PNH=45°,
∴∠HPN=∠PNH=45°,
∴△PHN是等腰直角三角形,
∴,
由题意得:,
∴,
设点P的坐标为(m,﹣m2+3m+4),则点N的坐标为(m,﹣m+4),
∴PN=﹣m2+3m+4﹣(﹣m+4)=﹣m2+4m=4,
解得:m=2,
∴﹣m2+3m+4=﹣22+3×2+4=6,
∴点P的坐标为(2,6);
(3)抛物线上存在点P,使∠CBP+∠ACO=45°;理由如下:
令y=0,则0=﹣x2+3x+4,
解得:x1=﹣1,x2=4,
∴A(﹣1,0),
如图2,将△AOC绕点O顺时针方向旋转90°至△A′OB,则A′O=AO=1,∠A′BO=∠ACO,
∴A′(0,1),
由(2)中的结论得,∠OBC=45°,
∵∠CBP+∠ACO=45°,
∴∠CBP=45°﹣∠ACO=∠OBC﹣∠A′BO=∠CBA′,
∴直线BA′上存在符合题意的点P,
设直线BA′的解析式为y=tx+n,将点B,点A′的坐标代入得:
,
解得:,
∴直线BA′的解析式为,
联立,
解得:或,
∴;
如图,连接CD、BD,过点B作BE⊥CD交于点E,
∵C(0,4),D(3,4),
∴CD∥x轴,
∵BE⊥CD,B(4,0),
∴∠E=90°,DE=4﹣3=1,BE=4,
∴CE=CD+DE=3+1=4,
∴CE=BE=4,
∴△CBE是等腰直角三角形,
∴∠CBE=45°,
∵AO=1,OC=4,
∴DE=AO,BE=OC,
又∵∠E=∠AOC=90°,
姑△BDE和△CAO中,
,
∴△BDE≌△CAO(SAS),
∴∠DBE=∠ACO,
∵∠CBP+∠ACO=45°,
∴∠CBP=45°﹣∠ACO=∠CBE﹣∠DBE=∠CBD,
∴直线BD上也存在符合题意的点P,
又∵点D(3,4)在抛物线上,
∴点P与点D重合,即P(3,4);
∴综上所述,抛物线上存在点P,使∠CBP+∠ACO=45°;点P的坐标为或(3,4).
16.【解答】解:(1)∵二次函数y=ax2+bx+4(a≠0)的图象经过点A(﹣4,0),B(1,0),
∴,
解得:,
∴该二次函数的表达式为y=﹣x2﹣3x+4;
(2)如图,设BP与y轴交于点E,
∵PD∥y轴,
∴∠DPB=∠OEB,
∵∠DPB=2∠BCO,
∴∠OEB=2∠BCO,
∴∠ECB=∠EBC,
∴BE=CE,
令x=0,得y=4,
∴C(0,4),OC=4,
设OE=a,则CE=4﹣a,
∴BE=4﹣a,
在Rt△BOE中,由勾股定理得:BE2=OE2+OB2,
∴(4﹣a)2=a2+12,
解得:a,
∴E(0,),
设BE所在直线表达式为y=kx+e(k≠0),
∴,
解得:,
∴直线BP的表达式为yx;
(3)有最大值.
如图,设PD与AC交于点N,
过点B作y轴的平行线与AC相交于点M,
设直线AC表达式为y=mx+n,
∵A(﹣4,0),C(0,4),
∴,
解得:,
∴直线AC表达式为y=x+4,
∴M点的坐标为(1,5),
∴BM=5,
∵BM∥PN,
∴△PNQ∽△BMQ,
∴,
设P(a0,﹣a02﹣3a0+4)(﹣4<a0<0),则N(a0,a0+4),
∴,
∴当a0=﹣2时,有最大值,
此时,点P的坐标为(﹣2,6).
17.【解答】解:(1)∵A(﹣1,0),B(4,0)是抛物线yx2+bx+c与x轴的两个交点,且二次项系数a,
∴根据抛物线的两点式知,y.
(2)根据抛物线表达式可求C(0,2),即OC=2.
∴2,
∵∠AOC=∠COB=90°,
∴△AOC∽△COB,
∴∠ACO=∠CBO,
∴∠QAB=∠QAC+∠CAO=∠CBA+45°+∠CAO=∠ACO+∠CAO+45°=135°,
∴∠BAP=180°﹣∠QAB=45°,
设P(m,n),且过点P作PD⊥x轴于D,则△ADP是等腰直角三角形,
∴AD=PD,即m+1=﹣n①,
又∵P在抛物线上,
∴②,
联立①②两式,解得m=6(﹣1舍去),此时n=﹣7,
∴点P的坐标是(6,﹣7).
(3)设PH与x轴的交点为Q1,P(a,),
则H(a,),PH,
若FP=FH,则∠FPH=∠FHP=∠BHQ1=∠BCO,
∴tan∠APQ1=tan∠BCO=2,
∴AQ1=2PQ1,
即a+1=2(),
解得a=3(﹣1舍去),此时PH.
若PF=PH,过点F作FM⊥y轴于点M,
∴∠PFH=∠PHF,
∵∠CFA=∠PFH,∠Q1HB=∠PHF,
∴∠CFA=∠Q1HB,
又∵∠ACF=∠BQ1H=90°,
∴△ACF∽△BQ1H,
∴CFAC,
在Rt△CMF中,MF=1,CM,
F(1,),
∴AF:,
将上式和抛物线解析式联立并解得x(﹣1舍去),
此时 PH.
若HF=HP,过点C作CE∥AB交AP于点E(见图),
∵∠CAF+∠CFA=90°,
∠PAQ+∠HPF=90°,
∠CFA=∠HFP=∠HPF,
∴∠CAF=∠PAQ1,
即 AP平分∠CAB,
∴CE=CA,
∴E(,2),
∴AE:,
联立抛物线解析式,解得x=5(﹣1舍去).
此时 PH.
∴当FP=FH时,PH;
当PF=PH时,PH;
当HF=HP时,PH;
18.【解答】解:(1)设抛物线的表达式为y=a(x﹣x1)(x﹣x2),
则y=a(x+2)(x﹣4)=ax2﹣2ax﹣8a,
即﹣8a=4,解得a,
故抛物线的表达式为yx2+x+4①;
(2)由点A、B的坐标知,OB=2OA,
故CO将△ABC的面积分成2:1两部分,此时,点P不在抛物线上;
如图1,当BHAB=2时,CH将△ABC的面积分成2:1两部分,
即点H的坐标为(2,0),
则CH和抛物线的交点即为点P,
由点C、H的坐标得,直线CH的表达式为y=﹣2x+4②,
联立①②并解得(不合题意的值已舍去),
故点P的坐标为(6,﹣8);
(3)在OB上取点E(2,0),则∠ACO=∠OCE,
∵∠OCA=∠OCB﹣∠OMA,故∠AMO=∠ECB,
过点E作EF⊥BC于点F,
在Rt△BOC中,由OB=OC知,∠OBC=45°,
则EFEB(4﹣2)BF,
由点B、C的坐标知,BC=4,
则CF=BC﹣BF=43,
则tan∠ECBtan∠AMO,
则tan∠AMO,
则OM=6,
故CM=OM±OC=6±4=2或10,
则t=2或10.
19.【解答】解:(1)令x=0,则y=4,
∴C(0,4);
令y=0,则x2x+4=0,
∴x=﹣2或x=3,
∴A(﹣2,0),B(3,0).
故答案为:(﹣2,0);(3,0);(0,4).
(2)①∵CP∥x轴,C(0,4),
∴P(1,4),
∴CP=1,AB=5,
∵CP∥x轴,
∴.
②如图,过点P作PQ∥AB交BC于点Q,
∴直线BC的解析式为:yx+4.
设点P的横坐标为m,
则P(m,m2m+4),Q(m2m,m2m+4).
∴PQ=m﹣(m2m)m2m,
∵PQ∥AB,
∴(m)2,
∴当m时,的最大值为.
另解:分别过点P,A作y轴的平行线,交直线BC于两点,仿照以上解法即可求解.
(3)假设存在点P使得∠BCO+2∠BCP=90°,即0<m<3.
过点C作CF∥x轴交抛物线于点F,
∵∠BCO+2∠PCB=90°,∠BCO+∠BCM+∠MCF=90°,
∴∠MCF=∠BCP,
延长CP交x轴于点M,
∵CF∥x轴,
∴∠PCF=∠BMC,
∴∠BCP=∠BMC,
∴△CBM为等腰三角形,
∵BC=5,
∴BM=5,OM=8,
∴M(8,0),
∴直线CM的解析式为:yx+4,
令x2x+4x+4,
解得x或x=0(舍),
∴存在点P满足题意,此时m.
20.【解答】解:(1)设抛物线的表达式为y=a(x﹣2)2﹣4,
将O(0,0)代入得:4a﹣4=0,
解得a=1,
∴y=(x﹣2)2﹣4=x2﹣4x;
(2)过A作AT⊥y轴于T,过P作PK⊥x轴于K,如图:
设P(m,m2﹣4m),
在y=x2﹣4x中,令y=0得x=0或x=4,
∴B(4,0);
∵∠AOB+∠AOT=90°,∠AOB+∠PBO=90°,
∴∠AOT=∠PBO,
∵∠ATO=90°=∠PKB,
∴△AOT∽△PBK,
∴,
∵A(2,﹣4),
∴,
解得m或m=4(此时P与B重合,舍去),
∴P(,).
21.【解答】解:(1)设抛物线的表达式为:y=a(x+3)(x﹣4)=a(x2﹣x﹣12),
即﹣12a=4,则a,
故抛物线的表达式为:yx2x+4①;
(2)在Rt△AOC中,tan∠CAO,
∵∠CAO+∠ABP=90°,
则tan∠ABP,
故设直线BP的表达式为:y(x﹣4)②,
联立①②得:x2x+4(x﹣4),
解得:xx0(不合题意的值已舍去);
(3)作∠EAG=∠BCD,
设AG=2BC=2×48,
∵AE=2CD,
∴△BCD∽△GAE且相似比为1:2,
则EG=2BD,
故当C、E、G共线时,CE+2BD=CE+EG=CG为最小,
在△ABC中,设AC边上的高为h,
则S△ABCAC hAB×CO,
即5h=4×7,
解得:h,
则sin∠ACBsin∠EAG,
则tan∠EAG=7,
过点G作GN⊥x轴于点N,
则NG=AG sin∠EAG,
即点G的纵坐标为:,
同理可得,点G的横坐标为:,
即点G(,),
由点C、G的坐标得,CG,
即CE+2BD的最小值为.
21世纪教育网(www.21cnjy.com)
同课章节目录
