2025年九年级中考数学三轮冲刺练习 二次函数中的面积问题 (无答案)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺练习 二次函数中的面积问题 (无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 310.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-09 00:00:00 | ||
图片预览


文档简介
2025年九年级中考数学三轮冲刺练习二次函数中的面积问题
二次函数中的面积问题是中考的热点,面积问题如果是规则图形可以用常见的面积公式解决问题的就直接用面积公式,如果不能直接用面积公式在坐标系中处理面积问题,通常有以下三种思路:第一是割补法:分割求和、补形作差,其中用的最多的是铅垂线法;第二是同底等高利用平行线转化求面积;第三如果遇到的是面积比可以考虑用相似的性质得到线段比去解决相关问题。
【引例1】在平面直角坐标系中,已知、、,求△ABC的面积.
【铅垂法】
【方法梳理】
(1)求A、B两点水平距离,即水平宽;
(2)过点C作x轴垂线与AB交于点D,可得点D横坐标同点C;
(3)求直线AB解析式并代入点D横坐标,得点D纵坐标;
(4)根据C、D坐标求得铅垂高;
(5).
二、转化法——借助平行线转化:
若S△ABP=S△ABQ, 若S△ABP=S△ABQ,
当P,Q在AB同侧时,PQ∥AB. 当P,Q在AB异侧时,AB平分PQ
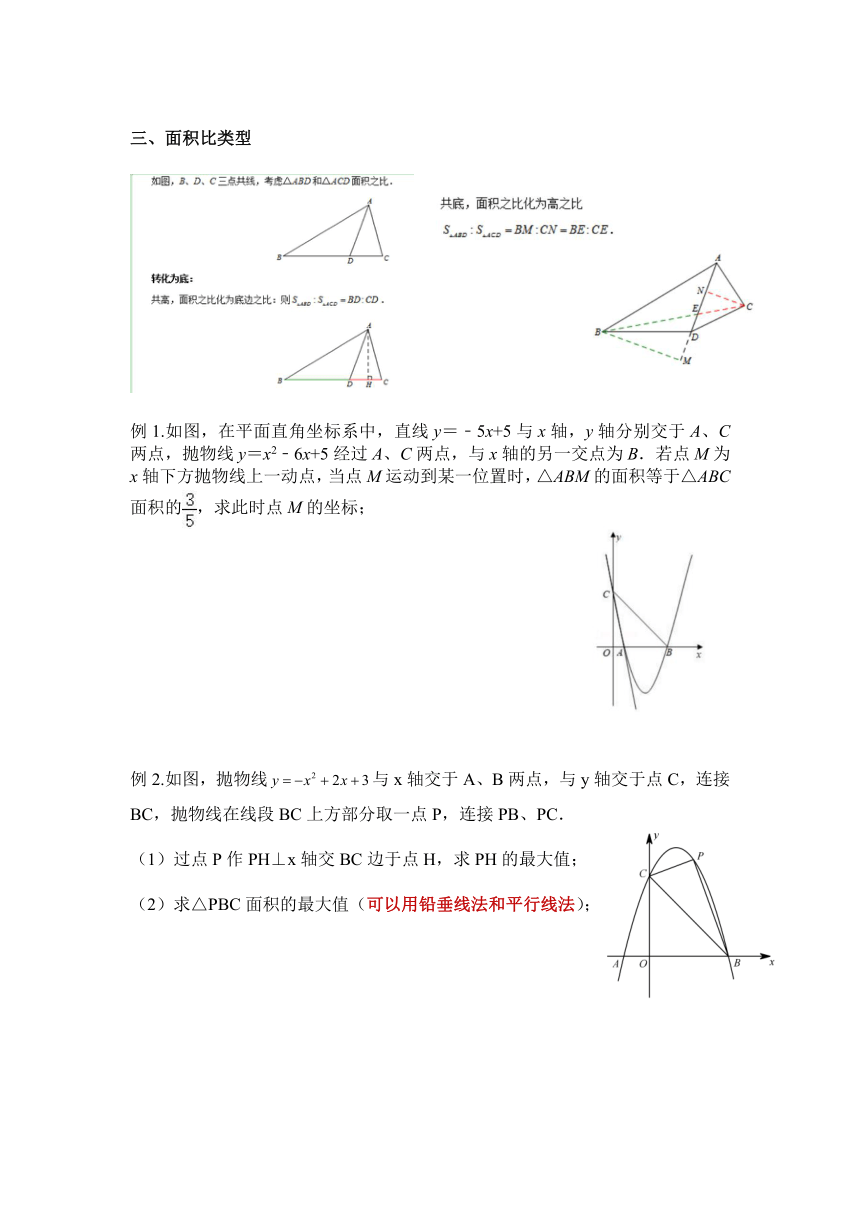
三、面积比类型
例1.如图,在平面直角坐标系中,直线y=﹣5x+5与x轴,y轴分别交于A、C两点,抛物线y=x2﹣6x+5经过A、C两点,与x轴的另一交点为B.若点M为x轴下方抛物线上一动点,当点M运动到某一位置时,△ABM的面积等于△ABC面积的,求此时点M的坐标;
例2.如图,抛物线与x轴交于A、B两点,与y轴交于点C,连接BC,抛物线在线段BC上方部分取一点P,连接PB、PC.
(1)过点P作PH⊥x轴交BC边于点H,求PH的最大值;
(2)求△PBC面积的最大值(可以用铅垂线法和平行线法);
变式1.如图,已知二次函数y=﹣x2+2x+3的图象经过点A(﹣1,0),B(3,0),与y轴交于点C.点D为抛物线的顶点,直线BC的解析式为y=﹣x+3,求△BCD的面积;
变式2.如图,抛物线y=﹣x2+4x﹣3;与x轴交于A,B两点,与y轴交于C点,直线BC方程为y=x﹣3.点P为抛物线上一点,若S△PBC=S△ABC,求P的坐标;
变式3.已知抛物线y=x2﹣2x﹣3经过(﹣1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.是否存在实数k使得△ABC的面积为?若存在,求出k的值;若不存在,请说明理由.
变式4.如图,在直角坐标系中,二次函数y=x2﹣2x﹣3的图象与x轴相交于点A(﹣1,0)和点B(3,0),与y轴交于点C.若点D为第四象限内二次函数图象上的动点,设点D的横坐标为m,△BCD的面积为S.求S关于m的函数关系式,并求出S的最大值.
例3.如图,抛物线y=﹣x2+4x﹣3与x轴交于点A(1,0)、B(3,0),与y轴交于点C,连接AC,BC.P为抛物线上一点,若S△PBC=S△ABC,求出点P的坐标;
【引例2】如图,抛物线y=﹣x2+x+4与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.当CP与x轴不平行时,求的最大值;(化斜为直)
例4.如图,抛物线y=﹣x2+2x+3与x轴交于点A和点B,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD,OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
变式1.抛物线y=x2﹣4x与直线y=x交于原点O和点B,与x轴交于另一点A,顶点为D.M是点B关于抛物线对称轴的对称点,Q是抛物线上的动点,它的横坐标为m(0<m<5),连接MQ,BQ,MQ与直线OB交于点E.设△BEQ和△BEM的面积分别为S1和S2,求的最大值.
变式2.已知:如图,二次函数y=﹣x2+x+4;点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
变式3.已知二次函数解析式为y=3x2﹣3,直线l的解析式为y=,点P为抛物线上第四象限上的一动点,过P作y轴的平行线交AD于M,作PN⊥AD于N,当△PMN面积有最大值时,求点P的坐标;
例4.如图抛物线y=﹣x2+2x+3经过点A(﹣1,0),点C(0,3),点P为抛物线上一点,连接CP,直线CP把四边形CBPA的面积分为3:5两部分,求点P的坐标.
变式1.已知抛物线y=x2﹣2x﹣3.与x轴交于A、B两点(点A在点B的左边),与y轴交于点C(0,﹣3),顶点D的坐标为(1,﹣4).若直线y=mx﹣m﹣4将四边形ACDB的面积分为1:2两部分,则m的值为多少
作业:1.已知二次函数y=2x2﹣8x+6的图象交x轴于A,B两点.若其图象上有且只有P1,P2,P3三点满足===m,则m的值是( )A.1 B. C.2 D.4
2.已知抛物线y=x2﹣x+3;经过A(3,0)、B(4,1)两点,且与y轴交于点C.设抛物线与x轴的另一个交点为D,在抛物线上是否存在点P,使△PAB的面积是△BDA面积的2倍?若存在,求出点P的坐标;若不存在,请说明理由.
3.如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0),C(0,3),点M是抛物线的顶点,点P为线段MB上一个动点,过点P作PD⊥x轴于点D,若OD=m.设△PCD的面积为S,试判断S有最大值或最小值吗?若有,求出其最值,若没有,请说明理由;
二次函数中的面积问题是中考的热点,面积问题如果是规则图形可以用常见的面积公式解决问题的就直接用面积公式,如果不能直接用面积公式在坐标系中处理面积问题,通常有以下三种思路:第一是割补法:分割求和、补形作差,其中用的最多的是铅垂线法;第二是同底等高利用平行线转化求面积;第三如果遇到的是面积比可以考虑用相似的性质得到线段比去解决相关问题。
【引例1】在平面直角坐标系中,已知、、,求△ABC的面积.
【铅垂法】
【方法梳理】
(1)求A、B两点水平距离,即水平宽;
(2)过点C作x轴垂线与AB交于点D,可得点D横坐标同点C;
(3)求直线AB解析式并代入点D横坐标,得点D纵坐标;
(4)根据C、D坐标求得铅垂高;
(5).
二、转化法——借助平行线转化:
若S△ABP=S△ABQ, 若S△ABP=S△ABQ,
当P,Q在AB同侧时,PQ∥AB. 当P,Q在AB异侧时,AB平分PQ
三、面积比类型
例1.如图,在平面直角坐标系中,直线y=﹣5x+5与x轴,y轴分别交于A、C两点,抛物线y=x2﹣6x+5经过A、C两点,与x轴的另一交点为B.若点M为x轴下方抛物线上一动点,当点M运动到某一位置时,△ABM的面积等于△ABC面积的,求此时点M的坐标;
例2.如图,抛物线与x轴交于A、B两点,与y轴交于点C,连接BC,抛物线在线段BC上方部分取一点P,连接PB、PC.
(1)过点P作PH⊥x轴交BC边于点H,求PH的最大值;
(2)求△PBC面积的最大值(可以用铅垂线法和平行线法);
变式1.如图,已知二次函数y=﹣x2+2x+3的图象经过点A(﹣1,0),B(3,0),与y轴交于点C.点D为抛物线的顶点,直线BC的解析式为y=﹣x+3,求△BCD的面积;
变式2.如图,抛物线y=﹣x2+4x﹣3;与x轴交于A,B两点,与y轴交于C点,直线BC方程为y=x﹣3.点P为抛物线上一点,若S△PBC=S△ABC,求P的坐标;
变式3.已知抛物线y=x2﹣2x﹣3经过(﹣1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.是否存在实数k使得△ABC的面积为?若存在,求出k的值;若不存在,请说明理由.
变式4.如图,在直角坐标系中,二次函数y=x2﹣2x﹣3的图象与x轴相交于点A(﹣1,0)和点B(3,0),与y轴交于点C.若点D为第四象限内二次函数图象上的动点,设点D的横坐标为m,△BCD的面积为S.求S关于m的函数关系式,并求出S的最大值.
例3.如图,抛物线y=﹣x2+4x﹣3与x轴交于点A(1,0)、B(3,0),与y轴交于点C,连接AC,BC.P为抛物线上一点,若S△PBC=S△ABC,求出点P的坐标;
【引例2】如图,抛物线y=﹣x2+x+4与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.当CP与x轴不平行时,求的最大值;(化斜为直)
例4.如图,抛物线y=﹣x2+2x+3与x轴交于点A和点B,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD,OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
变式1.抛物线y=x2﹣4x与直线y=x交于原点O和点B,与x轴交于另一点A,顶点为D.M是点B关于抛物线对称轴的对称点,Q是抛物线上的动点,它的横坐标为m(0<m<5),连接MQ,BQ,MQ与直线OB交于点E.设△BEQ和△BEM的面积分别为S1和S2,求的最大值.
变式2.已知:如图,二次函数y=﹣x2+x+4;点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
变式3.已知二次函数解析式为y=3x2﹣3,直线l的解析式为y=,点P为抛物线上第四象限上的一动点,过P作y轴的平行线交AD于M,作PN⊥AD于N,当△PMN面积有最大值时,求点P的坐标;
例4.如图抛物线y=﹣x2+2x+3经过点A(﹣1,0),点C(0,3),点P为抛物线上一点,连接CP,直线CP把四边形CBPA的面积分为3:5两部分,求点P的坐标.
变式1.已知抛物线y=x2﹣2x﹣3.与x轴交于A、B两点(点A在点B的左边),与y轴交于点C(0,﹣3),顶点D的坐标为(1,﹣4).若直线y=mx﹣m﹣4将四边形ACDB的面积分为1:2两部分,则m的值为多少
作业:1.已知二次函数y=2x2﹣8x+6的图象交x轴于A,B两点.若其图象上有且只有P1,P2,P3三点满足===m,则m的值是( )A.1 B. C.2 D.4
2.已知抛物线y=x2﹣x+3;经过A(3,0)、B(4,1)两点,且与y轴交于点C.设抛物线与x轴的另一个交点为D,在抛物线上是否存在点P,使△PAB的面积是△BDA面积的2倍?若存在,求出点P的坐标;若不存在,请说明理由.
3.如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0),C(0,3),点M是抛物线的顶点,点P为线段MB上一个动点,过点P作PD⊥x轴于点D,若OD=m.设△PCD的面积为S,试判断S有最大值或最小值吗?若有,求出其最值,若没有,请说明理由;
同课章节目录
