变量与函数
图片预览






文档简介
课件16张PPT。 变量与函数1、一辆汽车以30千米/时的速度行驶,行驶的路程s(千米)与行驶的时间t(小时)
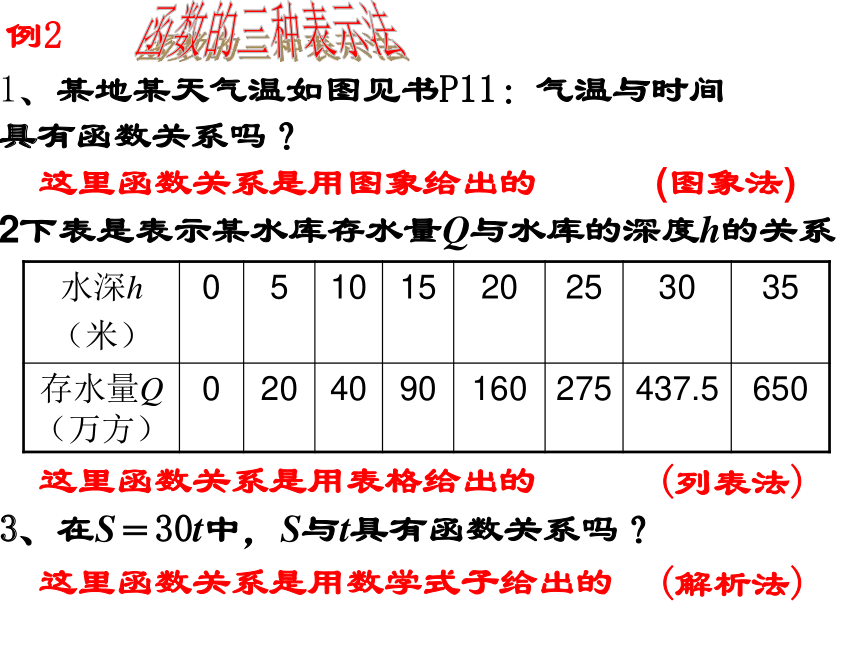
有怎样的关系呢?2、圆的面积S与半径r有怎样的关系?S=30tS=лr2 实例引入1、常量与变量的概念:常量:在某一变化过程中,始终保持不变的量.变量:在某一变化过程中,可以取不同数值的量.基本概念例1 指出下列关系式中的变量与常量1、球的表面积S(cm2)与球半径R(cm)的关系式是S=4лR22、设圆柱的底面半径R(m)不变,圆柱的体积V(m3 )与圆柱的高h(m)的关系式是V=лR2h3、以固定的速度V0(米/秒)向上抛一个球,小球的高度h(米)与小球运动的时间t(秒)之间的关系式是h=V0t-4.9t2我学会了吗?2、自变量、函数的概念 设在某一变化过程中有两个变量x和y,如果对于x的每一个值,y总有唯一的值与它对应,我们就说x是自变量,y是x的函数。概念整理例21、某地某天气温如图见书P11:气温与时间 具有函数关系吗?这里函数关系是用图象给出的这里函数关系是用表格给出的3、在S=30t中,S与t具有函数关系吗? 这里函数关系是用数学式子给出的
(图象法)
(列表法)(解析法)2下表是表示某水库存水量Q与水库的深度h的关系函数的三种表示法例3 用总长为60m的篱笆围成矩形场地,求矩形面积S(m2)与一边长l(m)之间的关系式,并指出式中的常量与变量,自变量与函数.
要围成一矩形场地,使一边靠墙,另三边用总长为60m的篱笆围成。
1.写出矩形面积S(m2)与平行于墙的一边长a(m)的关系式;
2.写出矩形面积S(m2)与垂直于墙的一边长a(m)的关系式;
3. 指出式中的常量与变量,函数与自变量.变式练习引例:
已知等腰三角形的周长为10,腰长为x,底边长为y,写出y与x的函数关系式,并求出x的取值范围.
说明:在用解析式表示函数时,要考虑自变量必须使解析式有意义的取值.灵活运用y与x的函数关系式为:试一试例1 求下列函数中自变量x的取值范围:
(1) y=3x-1; (2) y=2x2+7
(3) y= (4) y=(1)因为X取任意实数, 都有意义,所以x的取值范围是任意实数。(2)因为X取任意实数, 都有意义,所以x的取值范围是任意实数。(3)因为X+2不等于0时, 才有意义,所以x
的取值范围是:典型重点例题试一试: 求下列函数自变量的取值范围⑴ y= ⑵ y=
⑶ y= ⑷ y=
⑸ y= ⑹ y=说明:四种基本类型的函数自变量取值范围
1 整式-----一切实数 2 分式-----分母不为零
偶次根式 (被开方数≥0)
3 根式-----
奇次根式 (被开方数为一切实数 )
4 零指数-----底数≠0归纳延伸练习 1. 如图,用长35米的篱笆围成一个长方形的养鸡场,鸡场的一边靠墙(墙长18米),另三边用篱笆围成.设养鸡场宽AB为x米,面积为y平方米.
⑴ 求y与x函数关系;
⑵ 求x的取值范围;
⑶ 当养鸡场宽为多少时,面积等于150平方米.BACD墙再攀高峰! 2 . 拖拉机开始工作时,油箱中有油40升,如果每小时用油4升,求油箱中剩余油量y (升)与工作时间x (小时)之间的函数关系式, 并求x的取值范围.
再攀高峰! 例3 当MA=1 cm时,重叠部分的面积是多少?
解 :设重叠部分面积为y cm2,MA长为x cm,
容易求出y与x之间的函数关系式为 :
y=
当x=1时,y= 所以当MA=1 cm时,重叠部分的面积是 cm2 再攀高峰! 具有实际意义的函数 例2 如图,锐角△ABC中,BC=10,高AD=6,设EF为x.
⑴ 写出矩形面积S与x之间的函数关系式,并求出x的取值范围.
⑵ 当EF为多长时,S是SΔABC的一半?
ABCEMNDF再攀高峰!小结1. 四种基本类型的函数自变量取值范围 2. 具有实际意义的函数要考虑实际意义收获知多少?
有怎样的关系呢?2、圆的面积S与半径r有怎样的关系?S=30tS=лr2 实例引入1、常量与变量的概念:常量:在某一变化过程中,始终保持不变的量.变量:在某一变化过程中,可以取不同数值的量.基本概念例1 指出下列关系式中的变量与常量1、球的表面积S(cm2)与球半径R(cm)的关系式是S=4лR22、设圆柱的底面半径R(m)不变,圆柱的体积V(m3 )与圆柱的高h(m)的关系式是V=лR2h3、以固定的速度V0(米/秒)向上抛一个球,小球的高度h(米)与小球运动的时间t(秒)之间的关系式是h=V0t-4.9t2我学会了吗?2、自变量、函数的概念 设在某一变化过程中有两个变量x和y,如果对于x的每一个值,y总有唯一的值与它对应,我们就说x是自变量,y是x的函数。概念整理例21、某地某天气温如图见书P11:气温与时间 具有函数关系吗?这里函数关系是用图象给出的这里函数关系是用表格给出的3、在S=30t中,S与t具有函数关系吗? 这里函数关系是用数学式子给出的
(图象法)
(列表法)(解析法)2下表是表示某水库存水量Q与水库的深度h的关系函数的三种表示法例3 用总长为60m的篱笆围成矩形场地,求矩形面积S(m2)与一边长l(m)之间的关系式,并指出式中的常量与变量,自变量与函数.
要围成一矩形场地,使一边靠墙,另三边用总长为60m的篱笆围成。
1.写出矩形面积S(m2)与平行于墙的一边长a(m)的关系式;
2.写出矩形面积S(m2)与垂直于墙的一边长a(m)的关系式;
3. 指出式中的常量与变量,函数与自变量.变式练习引例:
已知等腰三角形的周长为10,腰长为x,底边长为y,写出y与x的函数关系式,并求出x的取值范围.
说明:在用解析式表示函数时,要考虑自变量必须使解析式有意义的取值.灵活运用y与x的函数关系式为:试一试例1 求下列函数中自变量x的取值范围:
(1) y=3x-1; (2) y=2x2+7
(3) y= (4) y=(1)因为X取任意实数, 都有意义,所以x的取值范围是任意实数。(2)因为X取任意实数, 都有意义,所以x的取值范围是任意实数。(3)因为X+2不等于0时, 才有意义,所以x
的取值范围是:典型重点例题试一试: 求下列函数自变量的取值范围⑴ y= ⑵ y=
⑶ y= ⑷ y=
⑸ y= ⑹ y=说明:四种基本类型的函数自变量取值范围
1 整式-----一切实数 2 分式-----分母不为零
偶次根式 (被开方数≥0)
3 根式-----
奇次根式 (被开方数为一切实数 )
4 零指数-----底数≠0归纳延伸练习 1. 如图,用长35米的篱笆围成一个长方形的养鸡场,鸡场的一边靠墙(墙长18米),另三边用篱笆围成.设养鸡场宽AB为x米,面积为y平方米.
⑴ 求y与x函数关系;
⑵ 求x的取值范围;
⑶ 当养鸡场宽为多少时,面积等于150平方米.BACD墙再攀高峰! 2 . 拖拉机开始工作时,油箱中有油40升,如果每小时用油4升,求油箱中剩余油量y (升)与工作时间x (小时)之间的函数关系式, 并求x的取值范围.
再攀高峰! 例3 当MA=1 cm时,重叠部分的面积是多少?
解 :设重叠部分面积为y cm2,MA长为x cm,
容易求出y与x之间的函数关系式为 :
y=
当x=1时,y= 所以当MA=1 cm时,重叠部分的面积是 cm2 再攀高峰! 具有实际意义的函数 例2 如图,锐角△ABC中,BC=10,高AD=6,设EF为x.
⑴ 写出矩形面积S与x之间的函数关系式,并求出x的取值范围.
⑵ 当EF为多长时,S是SΔABC的一半?
ABCEMNDF再攀高峰!小结1. 四种基本类型的函数自变量取值范围 2. 具有实际意义的函数要考虑实际意义收获知多少?
