7.7 动能和动能定理k课件(共31张PPT)
文档属性
| 名称 | 7.7 动能和动能定理k课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 251.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-12-10 00:00:00 | ||
图片预览










文档简介
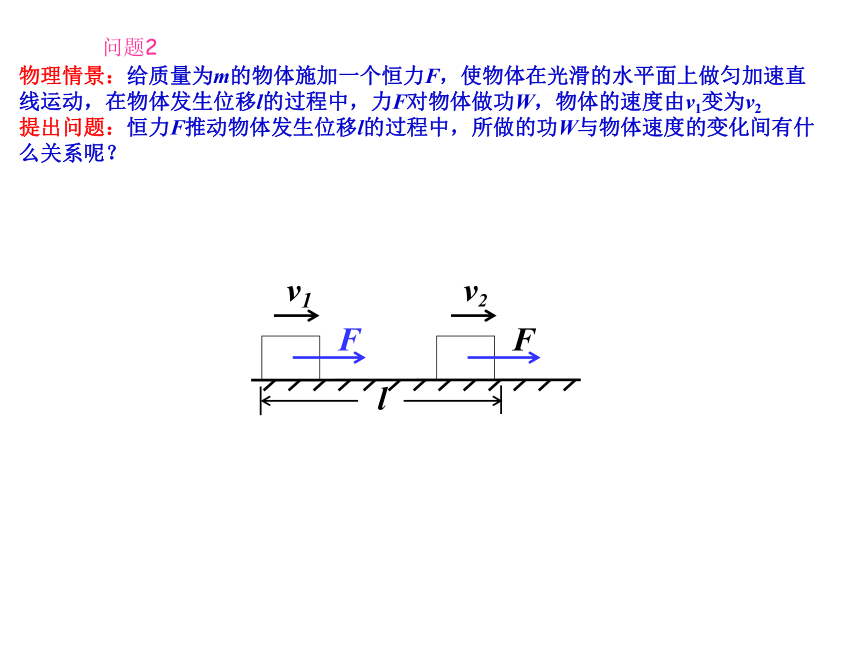
课件31张PPT。7.动能和动能定理回顾:1、什么叫动能?物体由于运动而具有的能量叫动能。2、动能跟哪些因素有关?质量和速度一、探究动能的表达式 问题1:学习重力势能时,是从哪里开始入手分析的?这对我们讨论动能有何启示?物理情景:给质量为m的物体施加一个恒力F,使物体在光滑的水平面上做匀加速直线运动,在物体发生位移l的过程中,力F对物体做功W,物体的速度由v1变为v2
提出问题:恒力F推动物体发生位移l的过程中,所做的功W与物体速度的变化间有什么关系呢?问题2提示:
(1)力F对物体做多少功?
(2)从牛顿运动定律角度分析,力F多大?
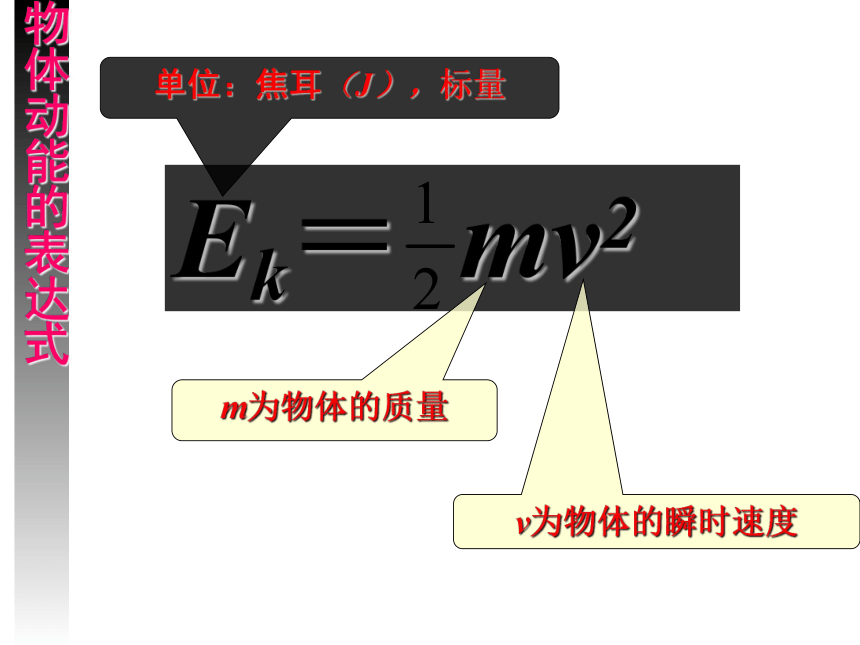
(3)从运动学角度分析,物体的初、末速度和位移之间的关系?结果与思考W= mv22- mv12初态和末态的表达式均为“mv2/2”,这个“mv2/2”代表什么?物体动能的表达式Ek= mv2m为物体的质量v为物体的瞬时速度单位:焦耳(J),标量例题1:我国发射的“神六”,质量为8吨,运行速度为7.5km/s,它的动能是多大? 1、改变汽车的质量和速度,都能使汽车的动能发生变化,在下面几种情况中,汽车的动能是原来2倍的是( ) A、质量不变,速度变为原来的2倍
B、质量和速度都变为原来的2倍
C、质量减半,速度变为原来的2倍
D、质量变为原来2倍,速度减半随堂练习C随堂练习2、下列关于一定质量的物体的速度和动能的说法中,正确的是( )
A、速度变化,动能一定变化
B、速度不变,动能一定不变
C、动能变化,速度一定变化
D、动能不变,速度可能变化B C D表达式:W=Ek2-Ek1W=mv22/2-mv12/2 内容:力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。二、动能定理对动能定理的理解W=Ek2-Ek1末动能初动能合力做的功即总功问题3:如果物体受到几个力的作用,动能定理中的W表示什么意义?对动能定理的理解 对任何过程的恒力、变力;直线运动、曲线运动都能运用。问题4:动能定理是在物体受恒力作用且做直线运动的情况下推出的。动能定理是否可以应用于变力做功或物体做曲线运动的情况,该怎样理解?动能定理:
牛顿运动定律:
例题2:一架喷气式飞机,质量m=5.0×103kg,起飞过程中从静止开始滑跑。当位移达到l=5.3×102m时,速度达到起飞速度v=60m/s。在此过程中飞机受到的平均阻力是飞机重量的0.02倍。求飞机受到的牵引力。F合=F-F阻=F- kmg =ma ②分别用牛顿运动定律和动能定理求解由动能定理得随堂练习 3、在距地面60m高处,以20m/s的速度竖直上抛一质量为m的物体,求物体落地时的速度。mgh= mv22- mv12先得出V2表达式,代入数据,得V2 = 40m/s变式1:其它条件都不变,若水平抛出,结果如何?变式2:若考虑空气阻力,且物体落地速度为V2 = 30m/s,m=2kg,能否求出阻力做的功? mgh+w阻= mv22- mv12代入数据,可得w阻=-700J应用动能定理解题的一般步骤:① 明确研究对象,明确运动过程.② 对研究对象进行受力分析(包括重力),
明确各力的做功大小及正负情况.有些
力在运动过程中不是始终存在,若物体
运动过程中包含几个物理过程,物体运
动状态受力情况均发生变化,因而在考
虑外力做功时,必须根据不同情况分别
对待找出各力所做的功并求总功:W总③ 明确始末状态,确定其动能(EK2,
EK1)及动能变化量(△Ek) (未知
量用符号表示),根据动能定理列出
方程:
W总=Ek2—Ek1 ④ 根据动能定理列方程求解并检验。常规题(匀变速直线运动)一质量为1kg的物体被人用手由静止向上提升1m,这时物体的速度2 m/s,则下列说法正确的是 ( )
A、手对物体做功 12J
B、合外力对物体做功 12J
C、合外力对物体做功 2J
D、物体克服重力做功 10 JACD解题时必须弄清是什么力做的功,有何特点?如何求?常规题(匀变速直线运动) 质量m=1.5kg的物体(可视为质点)在水平恒力F
作用下,从水平面上A点由静止开始运动,运动
一段距离后撤去该力,物体继续滑行t=2.0s停在
B点,已知A、B两点间的距离s=5.0m,物体与
水平面间的动摩擦因数μ=0.20,求恒力F多大?
(g=10m/s2)F=15N 匀变速直线运动 斜面问题练习:某物体放在倾角为θ的斜面上,向下轻轻一推,它刚好能匀速下滑;若给此物体一个沿斜面向上的初速度v0,那么,它能沿斜面向上冲滑的最大距离为多少? V02
4gsinθ求变力做功问题 (瞬间力做功问题)足球守门员在发门球时,将一个静止的质量为0.4
Kg的足球,以10m/s的速度踢出,这是足球获得的动能是 J。足球沿草地作直线运动,受到的阻力是足球重力的0.2倍。当足球运动到距发球点20m的后卫队员处时,速度为 m/s
(g=10m/s2)结论: 瞬间力做功直接转化为物体的初动能2020?
在离地面高为h处竖直上抛一质量为m的物块,抛出时的速度为V0,当它落到地面时速度为V,用
g表示重力加速度,则在此过程中物块克服空
气阻力所做得功等于,( )
A mgh-1/2mV2- mV02
B -1/2mV2- mV02-mgh
C mgh+1/2mV02-1/2mV2
D mgh+1/2mV2-1/2mV02
求变力做功问题 C求解曲线运动问题(圆周运动中的变力做功)
一个质量为m的小球拴在钢绳的一端,另一端受大小为F1的拉力作用,在水平面上做半径为R1匀速圆周运动(如图所示),今将力的大小改为F2时,使小球仍在水平面上做匀速圆周运动,但半径变为R2,小球运动的半径由R1变为R2过程中拉力对小球做的功多大?
W==W=?(F2R2-F1R1)求解曲线运动问题
如图所示,一固定在竖直平面内的光滑的半圆形轨道ABC,其半径R=0.5m,轨道在C处与水平地面相切。在C处放一小物块,给它一水平相左的初速度V0=5m/s,结果它沿CBA运动,通过A点,最后落在水平地面上的D点,求C、D间的距离。(g=10m/s2) ABCDS=1m质量为m的小球被系在轻绳的一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力的作用。设某一时刻小球通过轨道最低点,此时绳子的张力为7mg,此后小球继续做运动,经过半个圆周恰能通过最高点,则在此过程中小球克服空气阻力做的功为:( )C求解曲线运动问题(圆周运动中的变力做功)如图所示,质量为1kg的木块(可视为质点)静止在高1.2m的平台上,木块与平台间的动摩擦因数为0.2,用水平推力20N使木块产生位移3m时撤去,木块又滑行1m时飞出平台,求木块落地时速度的大小?多过程问题 (直线+曲线)全程列式:如图所示,小球从h高的光滑斜面上自静止滚下,经过有摩擦的水平面AB后再滚上另一光滑斜面,当它到达1/3h 高时的速度为零.试求小球最后静止的位置.多过程问题 (平面+斜面,多段)第1次,从左到右第2次返回,停在AB间停在AB中点质量为m的物体以速度v竖直向上抛出,物
体落回地面时,速度大小为3v/4,设物体在运动
中所受空气阻力大小不变,求:
(1)物体运动中所受阻力大小;
(2)物体以初速度2v竖直抛出时最大高度;
(3)若物体与地面碰撞中无机械能损失,
求物体运动的总路程。多过程问题 (往复运动)上升:下降:思考:可否全程列式? (2)物体以初速度2v竖直上抛(3)若物体与地面碰撞中无机械能损失,求物体运动的总路程。分析:物体最终必静止于地面全程列式:
(1)动能是标量, 对应于物
体的瞬时速度,使状态量,物体的运动
速度方向发生变化时,动能不变。
(2)当力做负功时,在动能定理的式中
应出现相应的负号。应用动能定理解易错点:
提出问题:恒力F推动物体发生位移l的过程中,所做的功W与物体速度的变化间有什么关系呢?问题2提示:
(1)力F对物体做多少功?
(2)从牛顿运动定律角度分析,力F多大?
(3)从运动学角度分析,物体的初、末速度和位移之间的关系?结果与思考W= mv22- mv12初态和末态的表达式均为“mv2/2”,这个“mv2/2”代表什么?物体动能的表达式Ek= mv2m为物体的质量v为物体的瞬时速度单位:焦耳(J),标量例题1:我国发射的“神六”,质量为8吨,运行速度为7.5km/s,它的动能是多大? 1、改变汽车的质量和速度,都能使汽车的动能发生变化,在下面几种情况中,汽车的动能是原来2倍的是( ) A、质量不变,速度变为原来的2倍
B、质量和速度都变为原来的2倍
C、质量减半,速度变为原来的2倍
D、质量变为原来2倍,速度减半随堂练习C随堂练习2、下列关于一定质量的物体的速度和动能的说法中,正确的是( )
A、速度变化,动能一定变化
B、速度不变,动能一定不变
C、动能变化,速度一定变化
D、动能不变,速度可能变化B C D表达式:W=Ek2-Ek1W=mv22/2-mv12/2 内容:力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。二、动能定理对动能定理的理解W=Ek2-Ek1末动能初动能合力做的功即总功问题3:如果物体受到几个力的作用,动能定理中的W表示什么意义?对动能定理的理解 对任何过程的恒力、变力;直线运动、曲线运动都能运用。问题4:动能定理是在物体受恒力作用且做直线运动的情况下推出的。动能定理是否可以应用于变力做功或物体做曲线运动的情况,该怎样理解?动能定理:
牛顿运动定律:
例题2:一架喷气式飞机,质量m=5.0×103kg,起飞过程中从静止开始滑跑。当位移达到l=5.3×102m时,速度达到起飞速度v=60m/s。在此过程中飞机受到的平均阻力是飞机重量的0.02倍。求飞机受到的牵引力。F合=F-F阻=F- kmg =ma ②分别用牛顿运动定律和动能定理求解由动能定理得随堂练习 3、在距地面60m高处,以20m/s的速度竖直上抛一质量为m的物体,求物体落地时的速度。mgh= mv22- mv12先得出V2表达式,代入数据,得V2 = 40m/s变式1:其它条件都不变,若水平抛出,结果如何?变式2:若考虑空气阻力,且物体落地速度为V2 = 30m/s,m=2kg,能否求出阻力做的功? mgh+w阻= mv22- mv12代入数据,可得w阻=-700J应用动能定理解题的一般步骤:① 明确研究对象,明确运动过程.② 对研究对象进行受力分析(包括重力),
明确各力的做功大小及正负情况.有些
力在运动过程中不是始终存在,若物体
运动过程中包含几个物理过程,物体运
动状态受力情况均发生变化,因而在考
虑外力做功时,必须根据不同情况分别
对待找出各力所做的功并求总功:W总③ 明确始末状态,确定其动能(EK2,
EK1)及动能变化量(△Ek) (未知
量用符号表示),根据动能定理列出
方程:
W总=Ek2—Ek1 ④ 根据动能定理列方程求解并检验。常规题(匀变速直线运动)一质量为1kg的物体被人用手由静止向上提升1m,这时物体的速度2 m/s,则下列说法正确的是 ( )
A、手对物体做功 12J
B、合外力对物体做功 12J
C、合外力对物体做功 2J
D、物体克服重力做功 10 JACD解题时必须弄清是什么力做的功,有何特点?如何求?常规题(匀变速直线运动) 质量m=1.5kg的物体(可视为质点)在水平恒力F
作用下,从水平面上A点由静止开始运动,运动
一段距离后撤去该力,物体继续滑行t=2.0s停在
B点,已知A、B两点间的距离s=5.0m,物体与
水平面间的动摩擦因数μ=0.20,求恒力F多大?
(g=10m/s2)F=15N 匀变速直线运动 斜面问题练习:某物体放在倾角为θ的斜面上,向下轻轻一推,它刚好能匀速下滑;若给此物体一个沿斜面向上的初速度v0,那么,它能沿斜面向上冲滑的最大距离为多少? V02
4gsinθ求变力做功问题 (瞬间力做功问题)足球守门员在发门球时,将一个静止的质量为0.4
Kg的足球,以10m/s的速度踢出,这是足球获得的动能是 J。足球沿草地作直线运动,受到的阻力是足球重力的0.2倍。当足球运动到距发球点20m的后卫队员处时,速度为 m/s
(g=10m/s2)结论: 瞬间力做功直接转化为物体的初动能2020?
在离地面高为h处竖直上抛一质量为m的物块,抛出时的速度为V0,当它落到地面时速度为V,用
g表示重力加速度,则在此过程中物块克服空
气阻力所做得功等于,( )
A mgh-1/2mV2- mV02
B -1/2mV2- mV02-mgh
C mgh+1/2mV02-1/2mV2
D mgh+1/2mV2-1/2mV02
求变力做功问题 C求解曲线运动问题(圆周运动中的变力做功)
一个质量为m的小球拴在钢绳的一端,另一端受大小为F1的拉力作用,在水平面上做半径为R1匀速圆周运动(如图所示),今将力的大小改为F2时,使小球仍在水平面上做匀速圆周运动,但半径变为R2,小球运动的半径由R1变为R2过程中拉力对小球做的功多大?
W==W=?(F2R2-F1R1)求解曲线运动问题
如图所示,一固定在竖直平面内的光滑的半圆形轨道ABC,其半径R=0.5m,轨道在C处与水平地面相切。在C处放一小物块,给它一水平相左的初速度V0=5m/s,结果它沿CBA运动,通过A点,最后落在水平地面上的D点,求C、D间的距离。(g=10m/s2) ABCDS=1m质量为m的小球被系在轻绳的一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力的作用。设某一时刻小球通过轨道最低点,此时绳子的张力为7mg,此后小球继续做运动,经过半个圆周恰能通过最高点,则在此过程中小球克服空气阻力做的功为:( )C求解曲线运动问题(圆周运动中的变力做功)如图所示,质量为1kg的木块(可视为质点)静止在高1.2m的平台上,木块与平台间的动摩擦因数为0.2,用水平推力20N使木块产生位移3m时撤去,木块又滑行1m时飞出平台,求木块落地时速度的大小?多过程问题 (直线+曲线)全程列式:如图所示,小球从h高的光滑斜面上自静止滚下,经过有摩擦的水平面AB后再滚上另一光滑斜面,当它到达1/3h 高时的速度为零.试求小球最后静止的位置.多过程问题 (平面+斜面,多段)第1次,从左到右第2次返回,停在AB间停在AB中点质量为m的物体以速度v竖直向上抛出,物
体落回地面时,速度大小为3v/4,设物体在运动
中所受空气阻力大小不变,求:
(1)物体运动中所受阻力大小;
(2)物体以初速度2v竖直抛出时最大高度;
(3)若物体与地面碰撞中无机械能损失,
求物体运动的总路程。多过程问题 (往复运动)上升:下降:思考:可否全程列式? (2)物体以初速度2v竖直上抛(3)若物体与地面碰撞中无机械能损失,求物体运动的总路程。分析:物体最终必静止于地面全程列式:
(1)动能是标量, 对应于物
体的瞬时速度,使状态量,物体的运动
速度方向发生变化时,动能不变。
(2)当力做负功时,在动能定理的式中
应出现相应的负号。应用动能定理解易错点:
