19.1.2函数的图象 同步练习(含答案)
文档属性
| 名称 | 19.1.2函数的图象 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 209.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 00:00:00 | ||
图片预览



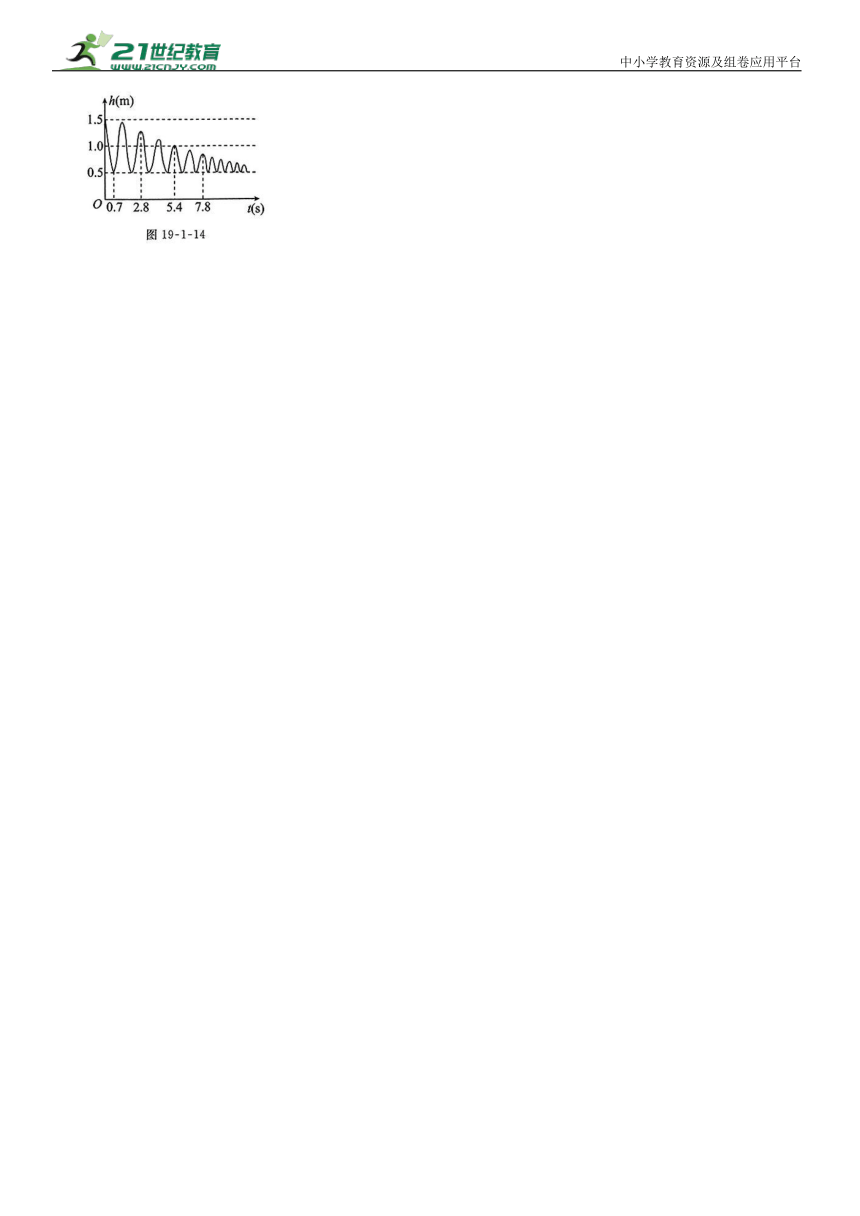
文档简介
19.1.2函数的图象
第1课时 函数的图象及其画法
知识要点分类练 夯实基础
知识点 1 函数图象的相关概念及画法
1.下列各点在函数y=2x-1图象上的是 ( )
A.(-1,3) B.(0,1)
C.(1,-1) D.(2,3)
2.小谢去学校,先从家匀速步行到校车停靠点,等几分钟后坐校车匀速去学校.已知小谢家、校车停靠点、学校在同一直线上,且校车停靠点在小谢家与学校之间,小谢离家的距离s(m)与时间t(min)之间的大致图象是 ( )
3. 若函数 y=2x+b(b为常数)的图象经过点(1,5),则b的值为 .
4.用描点法画出下列函数的图象:
(1)y=x-1;
知识点 2 从函数图象中读取信息
5. 如图19-1-7,曲线表示一只蝴蝶在飞行过程中离地面的高度h(m)随飞行时间 t(s)的变化情况,则这只蝴蝶飞行的最高高度约为( )
A. 5m B.7 m C.10 m D.13m
6.小明家、菜地、玉米地在同一条直线上.图19-1-8反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离家的距离.
(1)小明从家到菜地用了 分钟,菜地离小明家有 千米;
(2)小明给菜地浇水用了 分钟;
(3)小明从菜地到玉米地用了 分钟,菜地离玉米地有 千米;
(4)小明给玉米地锄草用了 分钟;
(5)玉米地离小明家的距离是多少 小明从玉米地回家的平均速度是多少
B规律方法综合练 训练思维
7.向如图 19-1-9 所示的空容器内匀速注水,从水刚接触底部时开始计时,直至把容器注满.在注水过程中,设容器内底部所受水的压强为 y(单位:帕),时间为x(单位:秒),则y关于x的函数图象大致为 ( )
8.第11届中国(湖南)国际矿物宝石博览会在我市举行,小方一家上午9:00开车前往会展中心参观.途中汽车发生故障,原地修车花了一段时间.车修好后,他们继续开车赶往会展中心.图19-1-11是他们家出发后离家的距离s与时间的函数图象.分析图中信息,下列说法正确的是 ( )
A.途中修车花了30 min
B.修车之前的平均速度是500 m/min
C.车修好后的平均速度是 800 m/min
D.车修好后的平均速度是修车之前的平均速度的1.5 倍
9. 下列图象中,表示y是x 的函数的是 ( )
10.地铁给人们带来了快捷、便利的生活,同时也是疏导交通、解决拥堵的最佳方式.现有甲、乙两个工程队分别同时开挖两条 600 米长的隧道,所挖隧道长度 y(米)与挖掘时间x(天)之间的函数关系如图19-1-13 所示.现有下列说法:
①甲队每天挖100米;
②乙队开挖2天后,每天挖50米;
③甲队比乙队提前2天完成任务;
④当x=2或x=6时,甲、乙两队所挖隧道长度相差100米.
其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
11. (1)画出函数 的图象;
(2)试判断点(-4,-6)是否在函数 y= 的图象上;
(3)从图象中观察,当x<0时,y随x的增大而增大,还是 y随x的增大而减小 当x>0时呢
拓广探究创新练 提升素养
12.小红帮弟弟荡秋千,秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图 19-1-14.
(1)根据函数的定义,请判断变量h是不是t的函数.
(2)结合图象回答:
①当t=0.7时,h的值是多少 说明它的实际意义;
②秋千摆动第一个来回需要多长时间
中小学教育资源及组卷应用平台
第2课时 函数的表示方法
A知识要点分类练 夯实基础
知识点 1 列表法
1. 弹簧原长(不挂重物)12 cm,弹簧总长 L(cm)与重物质量x(kg)的关系如下表所示:
重物质量x(kg) 0.5 1.0 1.5 2.0 2.5
弹簧总长 L(cm) 13 14 15 16 17
当重物质量为7.5kg(在弹性限度内)时,弹簧的总长 L(cm)是 ( )
A.27 B.27.5 C.20 D.19.5
2.某科研小组在网上获取了声音在空气中传播的速度与空气温度的关系的一些数据,如下表:
温度(℃) -20 -10 0 10 20 30
声速(m/s) 319 325 331 337 343 349
下列说法中错误的是 ( )
A.在这个问题中,温度是自变量,声速是温度的函数
B.空气温度每升高10℃,声速就增加6m /s
C.由表中数据可推测,在一定范围内,空气温度越高,声速越快
D.当空气温度为20℃时,声音5s 可以传播1745 m
3.心理学家发现,学生对概念的接受能力 y与提出概念所用的时间x(单位:分)之间有如下关系(其中2≤x≤20):
提出概念所用的时间x(分) 2 5 7 10 12 13 14 17 20
对概念的接受能力y 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
(1)上表反映了哪两个变量之间的关系
(2)当提出概念所用的时间是10分钟时,学生对概念的接受能力是多少
(3)根据表中的数据,你认为当提出概念所用的时间是几分钟时,学生对概念的接受能力最强
(4)从表中数据可知,当提出概念所用的时间x在什么范围内时,学生对概念的接受能力逐渐增强 当提出概念所用的时间x在什么范围内时,学生对概念的接受能力逐渐降低
知识点 2 解析式法
4.下表反映了一个图案中红色瓷砖和白色瓷砖的数量关系.设r和ω分别为一个图案中红色瓷砖和白色瓷砖的数量,下列函数解析式可以表示ω与r之间的关系的是 ( )
红色瓷砖的数量(r) 3 4 5 6 7
白色瓷砖的数量(w) 6 8 10 12 14
A. w=r+3 B. w=2r
D. w=r+7
5.某汽车生产厂对其生产的 A 型汽车进行油耗试验,试验中汽车为匀速行驶.汽车行驶过程中,油箱的剩余油量y(升)与行驶时间x(时)之间的关系如下表:
x(时) 0 1 2 3
y(升) 100 92 84 76
由表格中的数量关系可知,油箱的剩余油量y(升)与行驶时间x(时)之间的函数解析式为
知识点 3 图象法
6.小聪某次从家出发去公园游玩的行程如图19-1-15所示,他离家的路程为 s 米,所经过的时间为 t分钟,下列选项中的图象,能近似刻画s与t之间关系的是 ( )
7. 经科学家研究,蝉在气温超过28 ℃时才会活跃起来,此时边吸树木的汁液边鸣叫.如图19-1-17是某地一天的气温变化图象,在这一天中,听不到蝉鸣的时间有 .
B规律方法综合练 训练思维
8. 如图19-1-18,在△ABC中,∠C=60°,BC=3cm,AC=4 cm,点 P 从点 B 出发,沿B→C→A 的路径以1 cm/s的速度匀速运动到点 A.设点 P 的运动时间为 x s,B,P两点间的距离为y cm.
小新根据学习函数的经验,对函数 y 随自变量x 的变化规律进行了探究.
下面是小新的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x(s) 0 1 2 3 4 5 6 7
y(cm) 0 1.0 2.0 3.0 2.6 2.6 m 3.6
m的值是 ;
(2)建立平面直角坐标系,描出以表格中各组对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:在曲线部分的最低点时,在△ABC 中画出点 P 所在的位置,并求出此时点 P 运动的时间.
19.1.2 第1课时 函数的图象及其画法
1. D 2. B 3. 3 4. 略 5. D
6. (1)15 1.1 (2)10 (3)12 0.9 (4)18
(5)玉米地离小明家的距离是2千米,小明从玉米地回家的平均速度是 千米/分
7. B 8. D 9. B 10. D
11. (1)略 (2)点(-4,-6)不在函数 的图象上
(3)当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小
12.解:(1)因为对于每一个摆动时间t,都有一个唯一确定的h值与其对应,所以变量h是t的函数.
(2)①当t=0.7时,h=0.5,它的实际意义是秋千摆动0.7s时,离地面的高度为0.5m.
②2.8s.
第2课时 函数的表示方法
1. A 2. D
3. (1)反映了提出概念所用的时间x和对概念的接受能力y之间的关系
(2)59 (3)13分钟
(4)当2≤x≤13时,y值逐渐增大,即学生对概念的接受能力逐渐增强;当134. B 5. y=100-8x6. A 7. 12h
8. 解:(1)3.0
(2)描点、连线,画出图象,如图①所示.
(3)在曲线部分的最低点时,BP⊥AC,如图②所示.
因为∠C=60°,所以∠CBP=30°,
所以
此时点 P 运动的时间为(3+1.5)÷1=4.5(s).
第1课时 函数的图象及其画法
知识要点分类练 夯实基础
知识点 1 函数图象的相关概念及画法
1.下列各点在函数y=2x-1图象上的是 ( )
A.(-1,3) B.(0,1)
C.(1,-1) D.(2,3)
2.小谢去学校,先从家匀速步行到校车停靠点,等几分钟后坐校车匀速去学校.已知小谢家、校车停靠点、学校在同一直线上,且校车停靠点在小谢家与学校之间,小谢离家的距离s(m)与时间t(min)之间的大致图象是 ( )
3. 若函数 y=2x+b(b为常数)的图象经过点(1,5),则b的值为 .
4.用描点法画出下列函数的图象:
(1)y=x-1;
知识点 2 从函数图象中读取信息
5. 如图19-1-7,曲线表示一只蝴蝶在飞行过程中离地面的高度h(m)随飞行时间 t(s)的变化情况,则这只蝴蝶飞行的最高高度约为( )
A. 5m B.7 m C.10 m D.13m
6.小明家、菜地、玉米地在同一条直线上.图19-1-8反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离家的距离.
(1)小明从家到菜地用了 分钟,菜地离小明家有 千米;
(2)小明给菜地浇水用了 分钟;
(3)小明从菜地到玉米地用了 分钟,菜地离玉米地有 千米;
(4)小明给玉米地锄草用了 分钟;
(5)玉米地离小明家的距离是多少 小明从玉米地回家的平均速度是多少
B规律方法综合练 训练思维
7.向如图 19-1-9 所示的空容器内匀速注水,从水刚接触底部时开始计时,直至把容器注满.在注水过程中,设容器内底部所受水的压强为 y(单位:帕),时间为x(单位:秒),则y关于x的函数图象大致为 ( )
8.第11届中国(湖南)国际矿物宝石博览会在我市举行,小方一家上午9:00开车前往会展中心参观.途中汽车发生故障,原地修车花了一段时间.车修好后,他们继续开车赶往会展中心.图19-1-11是他们家出发后离家的距离s与时间的函数图象.分析图中信息,下列说法正确的是 ( )
A.途中修车花了30 min
B.修车之前的平均速度是500 m/min
C.车修好后的平均速度是 800 m/min
D.车修好后的平均速度是修车之前的平均速度的1.5 倍
9. 下列图象中,表示y是x 的函数的是 ( )
10.地铁给人们带来了快捷、便利的生活,同时也是疏导交通、解决拥堵的最佳方式.现有甲、乙两个工程队分别同时开挖两条 600 米长的隧道,所挖隧道长度 y(米)与挖掘时间x(天)之间的函数关系如图19-1-13 所示.现有下列说法:
①甲队每天挖100米;
②乙队开挖2天后,每天挖50米;
③甲队比乙队提前2天完成任务;
④当x=2或x=6时,甲、乙两队所挖隧道长度相差100米.
其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
11. (1)画出函数 的图象;
(2)试判断点(-4,-6)是否在函数 y= 的图象上;
(3)从图象中观察,当x<0时,y随x的增大而增大,还是 y随x的增大而减小 当x>0时呢
拓广探究创新练 提升素养
12.小红帮弟弟荡秋千,秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图 19-1-14.
(1)根据函数的定义,请判断变量h是不是t的函数.
(2)结合图象回答:
①当t=0.7时,h的值是多少 说明它的实际意义;
②秋千摆动第一个来回需要多长时间
中小学教育资源及组卷应用平台
第2课时 函数的表示方法
A知识要点分类练 夯实基础
知识点 1 列表法
1. 弹簧原长(不挂重物)12 cm,弹簧总长 L(cm)与重物质量x(kg)的关系如下表所示:
重物质量x(kg) 0.5 1.0 1.5 2.0 2.5
弹簧总长 L(cm) 13 14 15 16 17
当重物质量为7.5kg(在弹性限度内)时,弹簧的总长 L(cm)是 ( )
A.27 B.27.5 C.20 D.19.5
2.某科研小组在网上获取了声音在空气中传播的速度与空气温度的关系的一些数据,如下表:
温度(℃) -20 -10 0 10 20 30
声速(m/s) 319 325 331 337 343 349
下列说法中错误的是 ( )
A.在这个问题中,温度是自变量,声速是温度的函数
B.空气温度每升高10℃,声速就增加6m /s
C.由表中数据可推测,在一定范围内,空气温度越高,声速越快
D.当空气温度为20℃时,声音5s 可以传播1745 m
3.心理学家发现,学生对概念的接受能力 y与提出概念所用的时间x(单位:分)之间有如下关系(其中2≤x≤20):
提出概念所用的时间x(分) 2 5 7 10 12 13 14 17 20
对概念的接受能力y 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
(1)上表反映了哪两个变量之间的关系
(2)当提出概念所用的时间是10分钟时,学生对概念的接受能力是多少
(3)根据表中的数据,你认为当提出概念所用的时间是几分钟时,学生对概念的接受能力最强
(4)从表中数据可知,当提出概念所用的时间x在什么范围内时,学生对概念的接受能力逐渐增强 当提出概念所用的时间x在什么范围内时,学生对概念的接受能力逐渐降低
知识点 2 解析式法
4.下表反映了一个图案中红色瓷砖和白色瓷砖的数量关系.设r和ω分别为一个图案中红色瓷砖和白色瓷砖的数量,下列函数解析式可以表示ω与r之间的关系的是 ( )
红色瓷砖的数量(r) 3 4 5 6 7
白色瓷砖的数量(w) 6 8 10 12 14
A. w=r+3 B. w=2r
D. w=r+7
5.某汽车生产厂对其生产的 A 型汽车进行油耗试验,试验中汽车为匀速行驶.汽车行驶过程中,油箱的剩余油量y(升)与行驶时间x(时)之间的关系如下表:
x(时) 0 1 2 3
y(升) 100 92 84 76
由表格中的数量关系可知,油箱的剩余油量y(升)与行驶时间x(时)之间的函数解析式为
知识点 3 图象法
6.小聪某次从家出发去公园游玩的行程如图19-1-15所示,他离家的路程为 s 米,所经过的时间为 t分钟,下列选项中的图象,能近似刻画s与t之间关系的是 ( )
7. 经科学家研究,蝉在气温超过28 ℃时才会活跃起来,此时边吸树木的汁液边鸣叫.如图19-1-17是某地一天的气温变化图象,在这一天中,听不到蝉鸣的时间有 .
B规律方法综合练 训练思维
8. 如图19-1-18,在△ABC中,∠C=60°,BC=3cm,AC=4 cm,点 P 从点 B 出发,沿B→C→A 的路径以1 cm/s的速度匀速运动到点 A.设点 P 的运动时间为 x s,B,P两点间的距离为y cm.
小新根据学习函数的经验,对函数 y 随自变量x 的变化规律进行了探究.
下面是小新的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x(s) 0 1 2 3 4 5 6 7
y(cm) 0 1.0 2.0 3.0 2.6 2.6 m 3.6
m的值是 ;
(2)建立平面直角坐标系,描出以表格中各组对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:在曲线部分的最低点时,在△ABC 中画出点 P 所在的位置,并求出此时点 P 运动的时间.
19.1.2 第1课时 函数的图象及其画法
1. D 2. B 3. 3 4. 略 5. D
6. (1)15 1.1 (2)10 (3)12 0.9 (4)18
(5)玉米地离小明家的距离是2千米,小明从玉米地回家的平均速度是 千米/分
7. B 8. D 9. B 10. D
11. (1)略 (2)点(-4,-6)不在函数 的图象上
(3)当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小
12.解:(1)因为对于每一个摆动时间t,都有一个唯一确定的h值与其对应,所以变量h是t的函数.
(2)①当t=0.7时,h=0.5,它的实际意义是秋千摆动0.7s时,离地面的高度为0.5m.
②2.8s.
第2课时 函数的表示方法
1. A 2. D
3. (1)反映了提出概念所用的时间x和对概念的接受能力y之间的关系
(2)59 (3)13分钟
(4)当2≤x≤13时,y值逐渐增大,即学生对概念的接受能力逐渐增强;当13
8. 解:(1)3.0
(2)描点、连线,画出图象,如图①所示.
(3)在曲线部分的最低点时,BP⊥AC,如图②所示.
因为∠C=60°,所以∠CBP=30°,
所以
此时点 P 运动的时间为(3+1.5)÷1=4.5(s).
