20.2 数据的波动程度 同步练习(含答案)
文档属性
| 名称 | 20.2 数据的波动程度 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 147.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 19:44:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
20.2 数据的波动程度
第1课时 方差
知识要点分类练 夯实基础
知识点 1 方差的概念及计算
1.已知一组数据为2,3,4,5,6,则该组数据的方差为 ( )
A.2 B.4 C.6 D.10
2.某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如图 20-2-1所示,甲、乙两选手成绩的方差分别记为 s 甲,s ,则s 甲 s .(填“>”“<”或“=”)
3. 各10盒250毫升的甲、乙两种果汁饮料,检查其中的维生素C的含量,所得数据如下(单位:毫克):
甲:120,123,119,121,122,124,119,122,121,119;
乙:121,119,124,119,123,124,123,122,123,122.
通过计算说明哪种饮料维生素C的平均含量高,哪种饮料维生素C的含量比较稳定.
知识点 2 方差的简单应用
4.甲、乙、丙、丁四名同学参加立定跳远训练,他们成绩的平均数相同,方差如下: 则成绩最稳定的是 ( )
A.甲 B.乙 C.丙 D.丁
5.某班有40 人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他 39 人的平均分为90分,方差 后来小亮进行了补测,成绩为90分,该班 40人的测试成绩与该班39人的测试成绩相比,下列说法正确的是 ( )
A.平均分不变,方差变大
B.平均分不变,方差变小
C.平均分和方差都不变
D.平均分和方差都改变
6. 为了比较甲、乙、丙三种水稻秧苗的长势,每种秧苗各随机抽取40株,分别量出每株高度,计算发现三组秧苗的平均高度一样,并且得到甲、乙、丙三组秧苗高度的方差分别是3.6,10.8,15.8,由此可知 种秧苗长势更整齐(填“甲”“乙”或“丙”).
规律方法综合练 训练思维
7. 已知一组数据为7,2,5,x,8,它们的平均数是5,则这组数据的方差为 ( )
A.3 B.4.5
C.5.2 D.6
8.某同学在计算一组数据的方差时,得到了这样一个式子: 下列对于这组数据的描述,错误的是 ( )
A.平均数是7 B.中位数是5
C.众数是6 D.方差是3.2
9. 如图20-2-2所示是甲、乙两人10次射击成绩(单位:环)的条形图,则下列说法正确的是( )
A.甲比乙的成绩稳定
B.乙比甲的成绩稳定
C.甲、乙两人的成绩一样稳定
D.无法确定谁的成绩更稳定
10.某中学积极推进校园文学创作,倡导每名学生每学期向校报编辑部至少投1篇稿件.学期末,学校对七、八年级学生的投稿情况进行调查.
【数据的收集与整理】
分别从两个年级随机抽取相同数量的学生,统计每人在本学期投稿的篇数,制作了如下统计表:
投稿篇数 1 2 3 4 5
七年级人数 7 10 15 12 6
八年级人数 2 10 13 21 4
【数据的描述与分析】
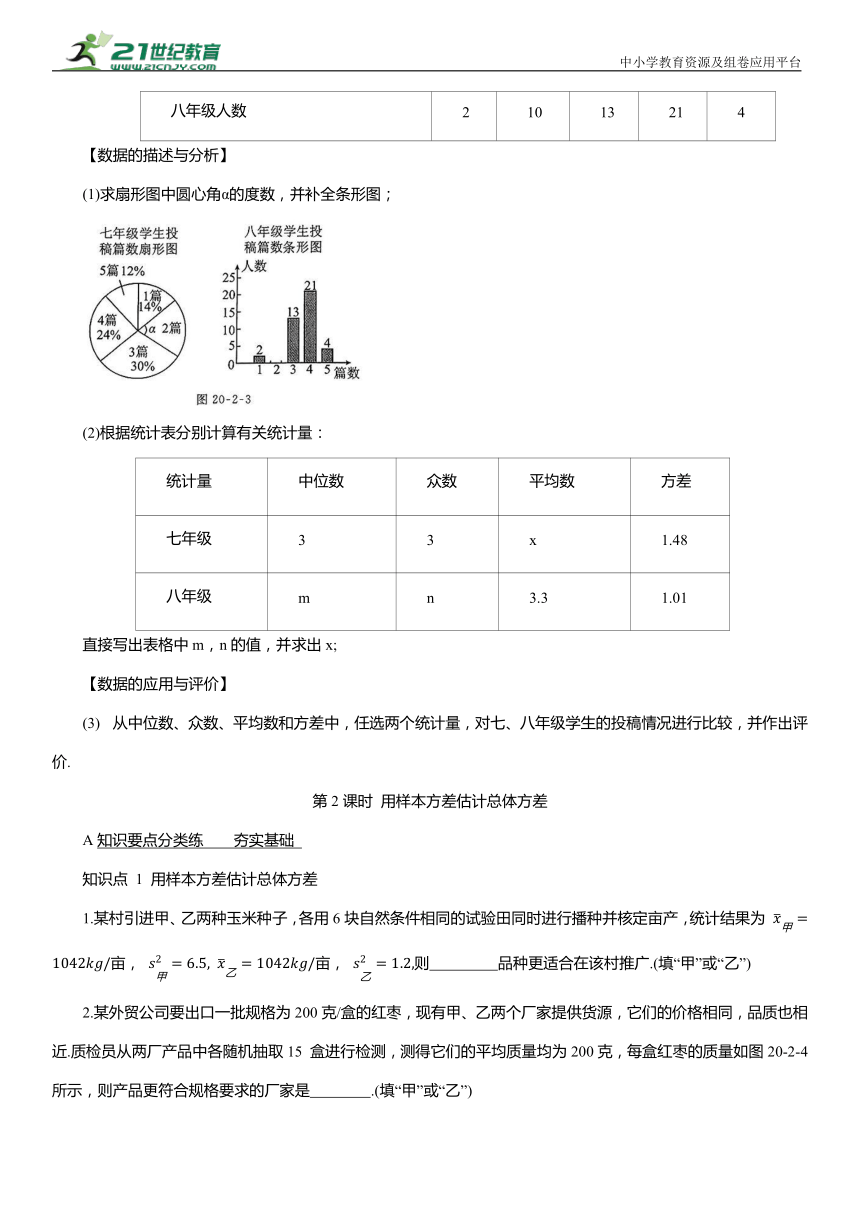
(1)求扇形图中圆心角α的度数,并补全条形图;
(2)根据统计表分别计算有关统计量:
统计量 中位数 众数 平均数 方差
七年级 3 3 x 1.48
八年级 m n 3.3 1.01
直接写出表格中m,n的值,并求出x;
【数据的应用与评价】
从中位数、众数、平均数和方差中,任选两个统计量,对七、八年级学生的投稿情况进行比较,并作出评价.
第2课时 用样本方差估计总体方差
A知识要点分类练 夯实基础
知识点 1 用样本方差估计总体方差
1.某村引进甲、乙两种玉米种子,各用6块自然条件相同的试验田同时进行播种并核定亩产,统计结果为 亩, 亩, 则 品种更适合在该村推广.(填“甲”或“乙”)
2.某外贸公司要出口一批规格为200克/盒的红枣,现有甲、乙两个厂家提供货源,它们的价格相同,品质也相近.质检员从两厂产品中各随机抽取15 盒进行检测,测得它们的平均质量均为200克,每盒红枣的质量如图20-2-4所示,则产品更符合规格要求的厂家是 .(填“甲”或“乙”)
3.近些年很多家庭喜欢在家里种植几株草莓,既可以美化环境,也为生活增添了乐趣.小华家今年种植了甲、乙两个品种的草莓各 10株,为了对两个品种的草莓进行比较并推荐给自己的好朋友,他将每株草莓的果实质量(单位:克)做了如下记录并分析:
甲 120 130 140 150 100 160 130 110 150 110
乙 110 160 170 140 130 190 60 80 100 160
分析:
平均数 中位数 方差
甲 130 130 s 甲
乙 130 a s z
根据以上信息,回答下列问题:
(1)表格中的a= ,s 甲 s (填“>”“=”或“<”);
(2)综合上表的分析,你认为小华应选择哪个品种的草莓推荐给好友 理由是什么
(3)通过预估,好朋友家的花园能够种植草莓100株,根据上面信息,分别求甲、乙两个品种可能收获果实多少克.
知识点 2 方差的变化规律
4. 已知一组数据a,b,c的平均数为5,方差为4,那么数据a-2,b-2,c-2的平均数和方差分别是( )
A.3,2 B.3,4 C.5,2 D.5,4
5.一组数据的方差为9,将这组数据中的每个数据都扩大为原来的2倍,则得到的一组新数据的方差是 .
规律方法综合练 训练思维
一组数据x ,x ,x ,x ,x ,x 的平均数是2,方差是5,则数据 的平均数是 ,方差是 .
拓广探究创新练 提升素养
7. 社会发展日新月异,企业唯有与时俱进,才能破茧成蝶、破壳发展.某醋厂秉持科技创新的理念,不断推陈出新.为开发一种新的风味醋,醋厂研发组采用甲、乙两种技术方案进行试验,每种方案各设置100个试验样品.经过一段时间后,研发组从两组试验样品中各随机抽取20个作为样本,对每个样本的指标进行综合评分(满分100,单位:分),并对相关数据进行整理和分析(用x表示综合评分,数据分成5组:A.50≤x<60;B.60≤x<70;C.70≤x<80;D.80≤x<90;E. x≥90.注:90分及以上为优等).
【数据收集与整理】
甲方案 20个样品的综合评分 59,86,77,87,78,73,79,69,84,91,85,91,64,85,59,78,64,70,75,86.
甲方案样本综合评分统计 A.50≤x<60 2
B.60≤x<70 3
C.70≤x<80 7
D.80≤x<90 6
E. x≥90 a
乙方案20个样品的综合评分 A,B,E组的数据个数相同,C组的所有数据是72,73,76,79,79.
乙方案样本综合评分统计
【数据分析】
样本综合评分情况分析 平均数 中位数 方差 优等率
甲方案 77 78 97.8 10%
乙方案 77 b 86.5 c
根据以上信息,解答下列问题:
(1)直接写出上述材料中空缺的数据:
(2)经过评估,研发组认为乙方案优于甲方案,你认为他们的结论合理吗 请结合“数据分析”中的四种数据说明理由;
(3)研发组计划对两种方案中综合评分为“优等”的试验样品进行第二阶段的指标分析,请估计第二阶段指标分析的试验样品共有多少个.
第1课时 方差
1. A 2. >
3.乙种饮料维生素C的平均含量高,甲种饮料维生素 C的含量比较稳定 说明略
4. D 5. B
6. 甲 7. C 8. B 9. B
10. (1)a=72°补全条形图略
(3)从平均数看,八年级投稿篇数的平均数高于七年级投稿篇数的平均数,所以八年级的投稿情况好于七年级;
从方差看,八年级投稿篇数的方差小于七年级投稿篇数的方差,说明八年级投稿篇数的波动较小,所以八年级投稿情况好于七年级.(答案合理即可)
第2课时 用样本方差估计总体方差
1. 乙 2. 甲
3. (1)135 <
(2)小华应选择甲品种的草莓推荐给好友.因为在平均数相同的情况下,甲品种的方差小于乙品种的方差,所以甲品种的果实质量更均匀(答案不唯一,合理即可).
(3)甲、乙两个品种可能收获果实均为13000克
4. B 5. 36 6. 7 20
7. 解:(1)2 79 15%
(2)合理.理由:根据统计表提供的信息,甲、乙两个方案样本综合评分的平均数相同,但是其他统计量不同.
从优等率看,乙方案为15%,甲方案为10%,说明乙方案优等试验样品的数量高于甲方案优等试验样品的数量,所以乙方案优于甲方案;
从中位数看,乙方案的中位数为79分,甲方案的中位数为78分,说明乙方案样本综合评分的中位数高于甲方案,所以乙方案优于甲方案;
从方差看,乙方案样本综合评分的方差小于甲方案样本综合评分的方差,说明乙方案的试验样品更为稳定.
综上所述,乙方案优于甲方案.
(3)100×(10%+15%)=25(个).
答:估计第二阶段指标分析的试验样品共有25个.
20.2 数据的波动程度
第1课时 方差
知识要点分类练 夯实基础
知识点 1 方差的概念及计算
1.已知一组数据为2,3,4,5,6,则该组数据的方差为 ( )
A.2 B.4 C.6 D.10
2.某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如图 20-2-1所示,甲、乙两选手成绩的方差分别记为 s 甲,s ,则s 甲 s .(填“>”“<”或“=”)
3. 各10盒250毫升的甲、乙两种果汁饮料,检查其中的维生素C的含量,所得数据如下(单位:毫克):
甲:120,123,119,121,122,124,119,122,121,119;
乙:121,119,124,119,123,124,123,122,123,122.
通过计算说明哪种饮料维生素C的平均含量高,哪种饮料维生素C的含量比较稳定.
知识点 2 方差的简单应用
4.甲、乙、丙、丁四名同学参加立定跳远训练,他们成绩的平均数相同,方差如下: 则成绩最稳定的是 ( )
A.甲 B.乙 C.丙 D.丁
5.某班有40 人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他 39 人的平均分为90分,方差 后来小亮进行了补测,成绩为90分,该班 40人的测试成绩与该班39人的测试成绩相比,下列说法正确的是 ( )
A.平均分不变,方差变大
B.平均分不变,方差变小
C.平均分和方差都不变
D.平均分和方差都改变
6. 为了比较甲、乙、丙三种水稻秧苗的长势,每种秧苗各随机抽取40株,分别量出每株高度,计算发现三组秧苗的平均高度一样,并且得到甲、乙、丙三组秧苗高度的方差分别是3.6,10.8,15.8,由此可知 种秧苗长势更整齐(填“甲”“乙”或“丙”).
规律方法综合练 训练思维
7. 已知一组数据为7,2,5,x,8,它们的平均数是5,则这组数据的方差为 ( )
A.3 B.4.5
C.5.2 D.6
8.某同学在计算一组数据的方差时,得到了这样一个式子: 下列对于这组数据的描述,错误的是 ( )
A.平均数是7 B.中位数是5
C.众数是6 D.方差是3.2
9. 如图20-2-2所示是甲、乙两人10次射击成绩(单位:环)的条形图,则下列说法正确的是( )
A.甲比乙的成绩稳定
B.乙比甲的成绩稳定
C.甲、乙两人的成绩一样稳定
D.无法确定谁的成绩更稳定
10.某中学积极推进校园文学创作,倡导每名学生每学期向校报编辑部至少投1篇稿件.学期末,学校对七、八年级学生的投稿情况进行调查.
【数据的收集与整理】
分别从两个年级随机抽取相同数量的学生,统计每人在本学期投稿的篇数,制作了如下统计表:
投稿篇数 1 2 3 4 5
七年级人数 7 10 15 12 6
八年级人数 2 10 13 21 4
【数据的描述与分析】
(1)求扇形图中圆心角α的度数,并补全条形图;
(2)根据统计表分别计算有关统计量:
统计量 中位数 众数 平均数 方差
七年级 3 3 x 1.48
八年级 m n 3.3 1.01
直接写出表格中m,n的值,并求出x;
【数据的应用与评价】
从中位数、众数、平均数和方差中,任选两个统计量,对七、八年级学生的投稿情况进行比较,并作出评价.
第2课时 用样本方差估计总体方差
A知识要点分类练 夯实基础
知识点 1 用样本方差估计总体方差
1.某村引进甲、乙两种玉米种子,各用6块自然条件相同的试验田同时进行播种并核定亩产,统计结果为 亩, 亩, 则 品种更适合在该村推广.(填“甲”或“乙”)
2.某外贸公司要出口一批规格为200克/盒的红枣,现有甲、乙两个厂家提供货源,它们的价格相同,品质也相近.质检员从两厂产品中各随机抽取15 盒进行检测,测得它们的平均质量均为200克,每盒红枣的质量如图20-2-4所示,则产品更符合规格要求的厂家是 .(填“甲”或“乙”)
3.近些年很多家庭喜欢在家里种植几株草莓,既可以美化环境,也为生活增添了乐趣.小华家今年种植了甲、乙两个品种的草莓各 10株,为了对两个品种的草莓进行比较并推荐给自己的好朋友,他将每株草莓的果实质量(单位:克)做了如下记录并分析:
甲 120 130 140 150 100 160 130 110 150 110
乙 110 160 170 140 130 190 60 80 100 160
分析:
平均数 中位数 方差
甲 130 130 s 甲
乙 130 a s z
根据以上信息,回答下列问题:
(1)表格中的a= ,s 甲 s (填“>”“=”或“<”);
(2)综合上表的分析,你认为小华应选择哪个品种的草莓推荐给好友 理由是什么
(3)通过预估,好朋友家的花园能够种植草莓100株,根据上面信息,分别求甲、乙两个品种可能收获果实多少克.
知识点 2 方差的变化规律
4. 已知一组数据a,b,c的平均数为5,方差为4,那么数据a-2,b-2,c-2的平均数和方差分别是( )
A.3,2 B.3,4 C.5,2 D.5,4
5.一组数据的方差为9,将这组数据中的每个数据都扩大为原来的2倍,则得到的一组新数据的方差是 .
规律方法综合练 训练思维
一组数据x ,x ,x ,x ,x ,x 的平均数是2,方差是5,则数据 的平均数是 ,方差是 .
拓广探究创新练 提升素养
7. 社会发展日新月异,企业唯有与时俱进,才能破茧成蝶、破壳发展.某醋厂秉持科技创新的理念,不断推陈出新.为开发一种新的风味醋,醋厂研发组采用甲、乙两种技术方案进行试验,每种方案各设置100个试验样品.经过一段时间后,研发组从两组试验样品中各随机抽取20个作为样本,对每个样本的指标进行综合评分(满分100,单位:分),并对相关数据进行整理和分析(用x表示综合评分,数据分成5组:A.50≤x<60;B.60≤x<70;C.70≤x<80;D.80≤x<90;E. x≥90.注:90分及以上为优等).
【数据收集与整理】
甲方案 20个样品的综合评分 59,86,77,87,78,73,79,69,84,91,85,91,64,85,59,78,64,70,75,86.
甲方案样本综合评分统计 A.50≤x<60 2
B.60≤x<70 3
C.70≤x<80 7
D.80≤x<90 6
E. x≥90 a
乙方案20个样品的综合评分 A,B,E组的数据个数相同,C组的所有数据是72,73,76,79,79.
乙方案样本综合评分统计
【数据分析】
样本综合评分情况分析 平均数 中位数 方差 优等率
甲方案 77 78 97.8 10%
乙方案 77 b 86.5 c
根据以上信息,解答下列问题:
(1)直接写出上述材料中空缺的数据:
(2)经过评估,研发组认为乙方案优于甲方案,你认为他们的结论合理吗 请结合“数据分析”中的四种数据说明理由;
(3)研发组计划对两种方案中综合评分为“优等”的试验样品进行第二阶段的指标分析,请估计第二阶段指标分析的试验样品共有多少个.
第1课时 方差
1. A 2. >
3.乙种饮料维生素C的平均含量高,甲种饮料维生素 C的含量比较稳定 说明略
4. D 5. B
6. 甲 7. C 8. B 9. B
10. (1)a=72°补全条形图略
(3)从平均数看,八年级投稿篇数的平均数高于七年级投稿篇数的平均数,所以八年级的投稿情况好于七年级;
从方差看,八年级投稿篇数的方差小于七年级投稿篇数的方差,说明八年级投稿篇数的波动较小,所以八年级投稿情况好于七年级.(答案合理即可)
第2课时 用样本方差估计总体方差
1. 乙 2. 甲
3. (1)135 <
(2)小华应选择甲品种的草莓推荐给好友.因为在平均数相同的情况下,甲品种的方差小于乙品种的方差,所以甲品种的果实质量更均匀(答案不唯一,合理即可).
(3)甲、乙两个品种可能收获果实均为13000克
4. B 5. 36 6. 7 20
7. 解:(1)2 79 15%
(2)合理.理由:根据统计表提供的信息,甲、乙两个方案样本综合评分的平均数相同,但是其他统计量不同.
从优等率看,乙方案为15%,甲方案为10%,说明乙方案优等试验样品的数量高于甲方案优等试验样品的数量,所以乙方案优于甲方案;
从中位数看,乙方案的中位数为79分,甲方案的中位数为78分,说明乙方案样本综合评分的中位数高于甲方案,所以乙方案优于甲方案;
从方差看,乙方案样本综合评分的方差小于甲方案样本综合评分的方差,说明乙方案的试验样品更为稳定.
综上所述,乙方案优于甲方案.
(3)100×(10%+15%)=25(个).
答:估计第二阶段指标分析的试验样品共有25个.
