鲁教版九年级下册期末综合测试卷 (一)(含答案)
文档属性
| 名称 | 鲁教版九年级下册期末综合测试卷 (一)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1019.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末综合测试卷 (一)
时间: 60分钟 满分: 120分
一、选择题(共10小题,每小题3分,共30分)
1.已知一次函数y= ax+b经过点(-2,-3),正比例函数y = ax不经过第三象限,则反比例函数 的图象位于 ( )
A.第一、第二象限 B.第一、第三象限
C.第二、第三象限 D.第二、第四象限
2.笔、墨、纸、砚是中国传统的文房四宝,是中国书法的必备用具,如图是寓意“规矩方圆”的一方砚台,它的俯视图是( )
3.二次函数 (n为常数)的图象经过点, B(- ,y ),C(0,y ),则 y ,y ,y 的大小关系是 ( )
4.如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD 的度数是 ( )
A.110° B.115° C.120° D.125°
5.从1,2,3这三个数中任取两数,分别记为m,n,那么点(m,n)在反比例函数 图象上的概率为 ( )
B. C.
6.某停车场入口的栏杆如图所示,栏杆从水平位置AB 绕点O旋转到A'B'的位置,已知AO=4m,若栏杆的旋转角. 时,借助计算器求栏杆 A 端升高的高度,下列按键顺序正确的是 ( )
7.为解决停车问题,某小区在如图所示的一段道路边开辟一段斜列式停车位,每个车位长6m,宽2.4m,矩形停车位与道路成60°角,则在这一路段边上最多可以划出 个车位(参考数据: ( )
A.7 B.8 C.9 D.10
8.如图,在平面直角坐标系中,边长为2 的正六边形 ABCDEF 的中心与原点O重合,AB∥x轴,交y轴于点 P.将△OAP绕点O顺时针旋转,每次旋转90°,则第2 024次旋转结束时,点A 的坐标为 ( )
D.(1, )
第8题图 第9题图
9.如图,菱形ACBD中,AB与CD 交于O点, ,以C为圆心、AC为半径作弧AB,再以点C为圆心,CO为半径作弧EF,分别交AC于F 点,BC于E点,若CB=2,则图中阴影部分的面积为 ( )
10.如图,抛物线 与x轴交于点A,B,与y轴交于点C,对称轴为直线x=-1,若点A 的坐标为(--4,0),则下列结论正确的是 ( )
C.若关于x的一元二次方程 的两根为 则
D.点 在抛物线上,当 时
二、填空题(共6小题,每小题3分,共18分)
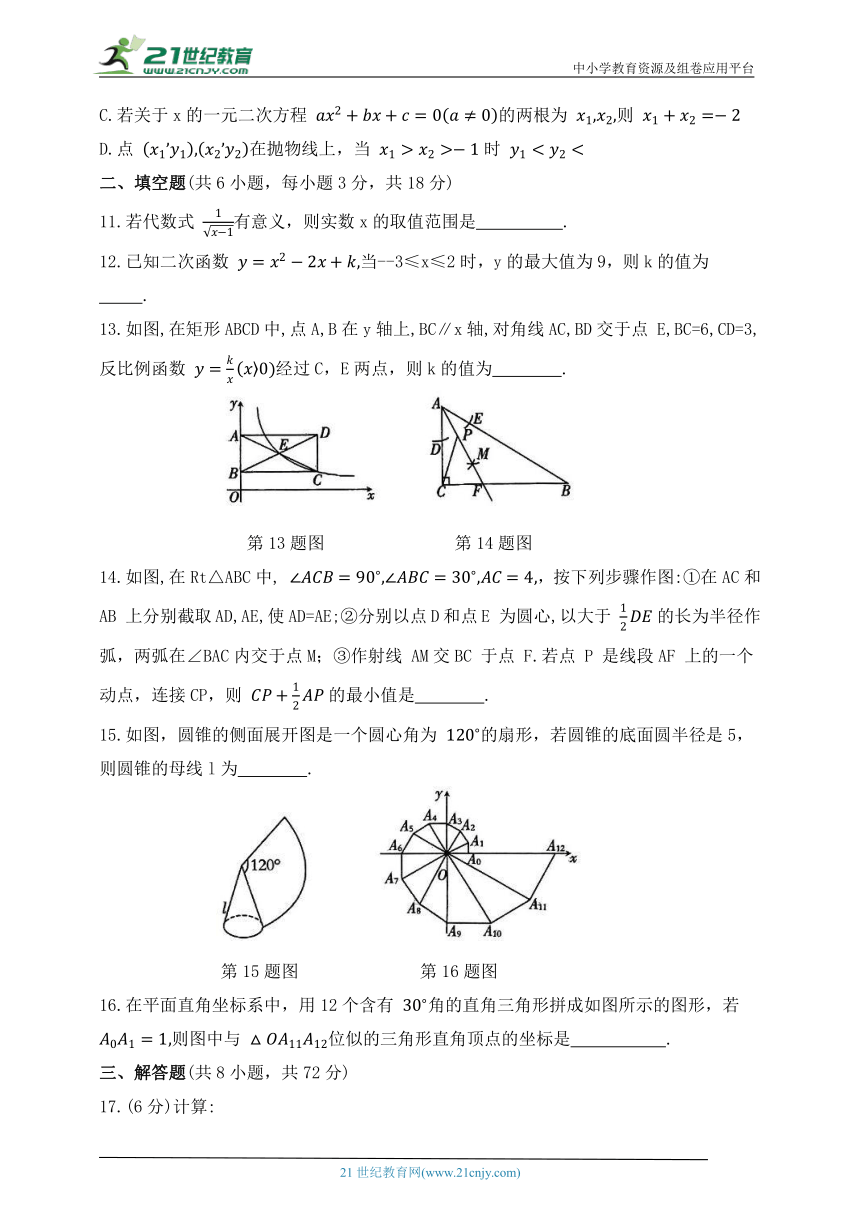
11.若代数式 有意义,则实数x的取值范围是 .
12.已知二次函数 当--3≤x≤2时,y的最大值为9,则k的值为 .
13.如图,在矩形ABCD中,点A,B在y轴上,BC∥x轴,对角线AC,BD交于点 E,BC=6,CD=3,反比例函数 经过C,E两点,则k的值为 .
第13题图 第14题图
14.如图,在Rt△ABC中, ,按下列步骤作图:①在AC和AB 上分别截取AD,AE,使AD=AE;②分别以点D和点E 为圆心,以大于 的长为半径作弧,两弧在∠BAC内交于点M;③作射线 AM交BC 于点 F.若点 P 是线段AF 上的一个动点,连接CP,则 的最小值是 .
15.如图,圆锥的侧面展开图是一个圆心角为 的扇形,若圆锥的底面圆半径是5,则圆锥的母线l为 .
第15题图 第16题图
16.在平面直角坐标系中,用12个含有 角的直角三角形拼成如图所示的图形,若 则图中与 位似的三角形直角顶点的坐标是 .
三、解答题(共8小题,共72分)
17.(6分)计算:
18.(7分)已知:如图,在平面直角坐标系中,一次函数. 与反比例函数 的图象交于点 A(2,m)和点 B,与x轴交于点 D.
(1)求m,a 及B 点坐标;
(2)根据图象直接写出不等式 的解集;
(3)若P 是x轴上一点,且满足 的面积等于5,求点 P 坐标.
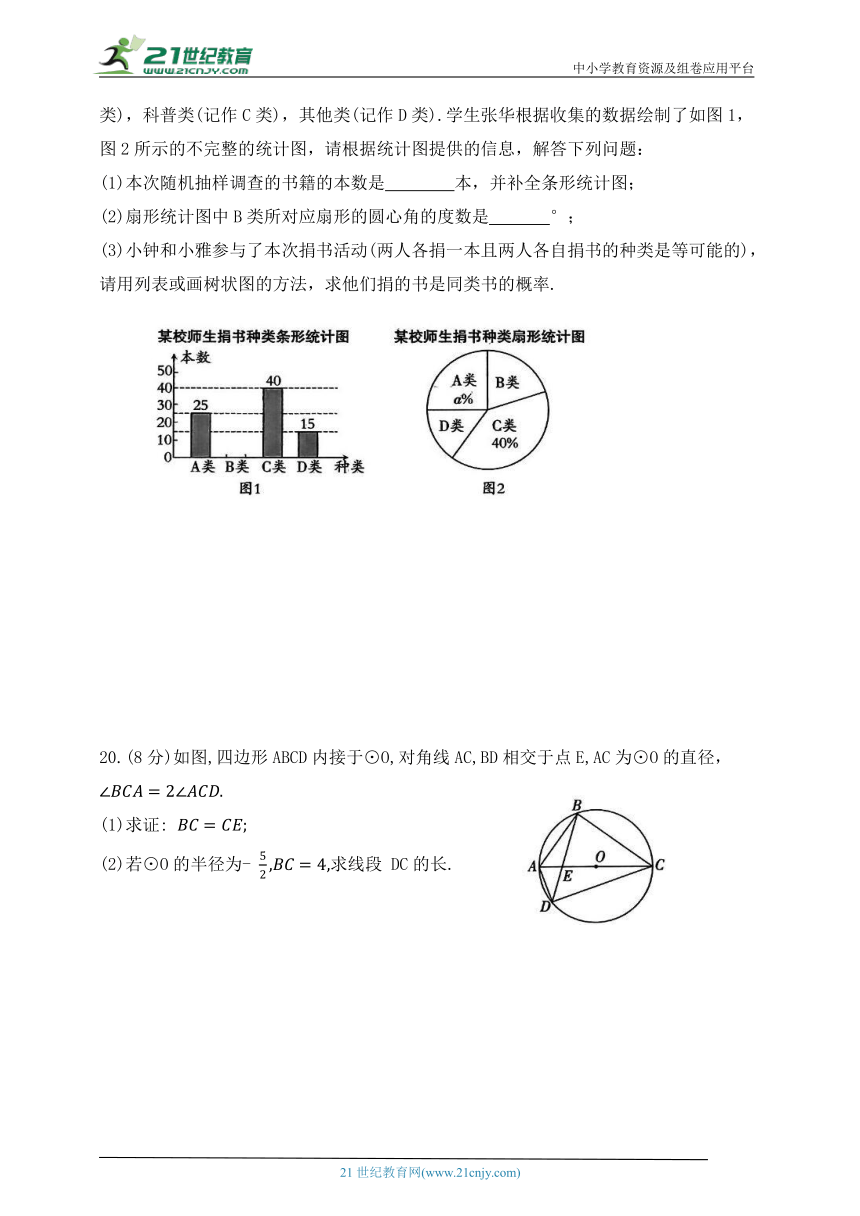
19.(8分)为提升学生的核心素养,长沙市某教育教学联合体开展了城乡读书交流活动.该教育教学联合体的某成员校号召全体师生积极捐书.为了解所捐书的种类,校团委对部分书籍进行了随机抽样调查,所捐书籍分为四类:文学类(记作 A类),艺术类(记作B类),科普类(记作C类),其他类(记作D类).学生张华根据收集的数据绘制了如图1,图2所示的不完整的统计图,请根据统计图提供的信息,解答下列问题:
(1)本次随机抽样调查的书籍的本数是 本,并补全条形统计图;
(2)扇形统计图中B类所对应扇形的圆心角的度数是 °;
(3)小钟和小雅参与了本次捐书活动(两人各捐一本且两人各自捐书的种类是等可能的),请用列表或画树状图的方法,求他们捐的书是同类书的概率.
20.(8分)如图,四边形ABCD内接于⊙O,对角线AC,BD相交于点E,AC为⊙O的直径,
(1)求证:
(2)若⊙O的半径为- 求线段 DC的长.
21.(9分)某农户生产经销一种农产品,已知这种产品的成本价为每千克20元.市场调查发现,该产品每天的销售价为25(元/千克)时,每天销售量为30(千克).当产品的销售价每千克涨1元时每天销售量会减少2千克,设涨价x(元/千克)(x为正整数),每天销售量为y(千克).
(1)直接写出y与x之间的函数关系式;
(2)该农户想要每天获得128元的销售利润,销售价为多少
(3)每千克涨价多少元时,每天的销售利润最大 最大利润是多少元
22.(10分)如图,甲、乙两艘货轮同时从A港出发,分别向 B,D两港运送物资,最后到达A港正东方向的C港装运新的物资.甲货轮沿A港的东南方向航行40海里后到达B港,再沿北偏东 方向航行一定距离到达C港.乙货轮沿 A港的北偏东( 方向航行一定距离到达D港,再沿南偏东 方向航行一定距离到达 C港.(参考数据:
(1)求A,C两港之间的距离(结果保留小数点后一位);
(2)若甲、乙两艘货轮的速度相同(停靠B,D两港的时间相同),哪艘货轮先到达C港 请通过计算说明.
23.(11分)如图,在△ABC中,∠ACB=90°,D是BC中点.
(1)尺规作图:以AC为直径作⊙O,交AB于点E保留作图痕迹。不需写作法);
(2)求证:DE是⊙O的切线;
(3)若AC=8,AB=10,求O到CE的距离.
在,请求上点D的坐标;看不是我,将就将摊向。
(3)如图2、点P容重线BC下面称根据线上,连接AP变程于坐轴,每10
24.(13分)已知抛物线 与x轴交于 B(6,0)两点,与y轴交于点(
(1)求抛物线的表达式;
(2)如图1,在对称轴上是否存在点 D,使 是以 BC 为直角边的直角三角形 若存在,请求出点 D 的坐标;若不存在,请说明理由;
(3)如图2,点 P 在直线BC 下方的抛物线上,连接AP 交BC 于点M,当 最大时,请直接写出点 P 的坐标.
参考答案
1. D 2. C 3. B 4. A 5. B 6. A 7. D 8. D 9. A 10. C
17.解:
18.解:(1)∵函数y=x+1的图象经过点 A(2,m),∴m=3,∴A(2,3),
∵点A(2,3)在反比例函数图象上,∴a=6,∴反比例函数表达式为
联立,得 解得 或 ∴B(-3,-2);
(2)由图象,得不等式 的解集为x<-3或0(3)设点 P坐标为(m,0),在y=x+1中,令y=0,则x=-1,∴D(-1,0),
∴m+1=±2,∴m=1或-3,∴点 P 坐标为(-3,0)或(1,0).
19.解:(1)本次随机抽样调查的书籍的本数是40÷40%=100(本),
∴B 类 的本数是 100--25--40--15 =20(本),
故答案为:100,
补全条形统计图如图1:
(2)扇形统计图中 B类所对应扇形的圆心角的度数是
故答案为:72;
(3)画树状图如图2:
共有16种等可能的结果,其中小钟和小雅捐的书是同类书的结果有4种,
∴他们捐的书是同类书的概率为
20.解:(1)证明:设∠ACD=α,则∠BCA=2∠ACD=2α,∴∠ABD=∠ACD=α,
∵AC为⊙O的直径,∴∠ABC=90°,∴∠CBE=∠ABC-∠ABD=90°-α,
∴∠CBE=∠CEB,∴BC=CE;
(2)过点 C作CT⊥BE于T,如图所示:
∵⊙O的半径为 ,BC=4,∴AC=5,
设AD=x,由(1),得 BC=CE=4,
AC-CE=5-4=1,
∵∠BCE=∠ADE,∠BEC=∠AED,∴△BCE∽△ADE,
∴AD:BC=AE:BE,即x:4=1: BE,
∵AC为⊙O的直径,CT⊥BE,∴∠ADC=∠ETC=90°,
∴∠ECT=∠ACD,∴△ECT∽△ACD,
∴AD:ET=AC:CE,即 (负值舍去),
在Rt△ACD中,
由勾股定理得
21.解:(1)由题意得:y=30-2x,
∵30-2x>0,∴x<15,
∴y与x之间的函数关系式为y=30-2x(0(2)设利润为ω元,则由题意得w=(x+25-20)(30-2x)=(x+5)(30-2x),
∵该农户想要每天获得128元的销售利润,
∴(x+5)(30-2x)=128,解得 (舍去),
∴销售价为25+11=36(元),
∴农户想要每天获得128元的销售利润,销售价为36元;
(3)w=(x+5)(30-2x)=-2(x-5) +200.
∵-2<0,∴当x=5时,w有最大值,最大值为200,
∴每千克涨价5元时,每天的销售利润最大,最大利润是200元.
22.解:(1)过点 B作BE⊥AC,垂足为 E,
在 Rt△ABE中, 40海里,
(海里), (海里),在 Rt△BCE中,∠CBE=60°,
(海里),
(海里),
∴A,C两港之间的距离约为77.2海里;
(2)甲货轮先到达C港,
理由:
由题意得∠CDF=30°,DF∥AG,∴∠GAD=∠ADF=60°,
∴∠ADC=∠ADF+∠CDF=90°,在 Rt△ACD 中, 30°,
海里,海里,
在 Rt△BCE中, 海里,海里),
∴甲货轮航行的路程=AB+BC=40+ 4(海里),
乙货轮航行的路程=AD+CD=10 105.4(海里),
∵96.4 海里<105.4海里,∴甲货轮先到达C港.
23.解:(1)如图,⊙O即为所求作;
(2)证明:如图,连接OE,CE,
∵AC为⊙O的直径,∴∠AEC=90°,∴∠CEB=90°,
∵D是BC中点,∴∠DCE=∠DEC,
∵OC=OE,∴∠OCE=∠OEC,
∴∠OED=∠OEC+∠DEC=∠OCE+∠DCE=∠ACB=90°,
∵OE是⊙O的半径,∴DE是⊙O的切线;
(3)如图,过点O作OF⊥CE于点F,∴F是CE 的中点,
∵O是AC 的中点,∴OF 是△ACE的中位线,
在△ABC中,∠ACB=90°,∵AC=8,AB=10,
∴10CE=8×6,∴CE=4.8,
∴OF=3.2,
∴O到CE 的距离为3.2.
24.解:(1)将点 A(-2,0),B(6,0),C(0,-3)代入 得
解得
(2)存在,理由:
如图1,当∠CBD=90°时,
过点 B作GH⊥x轴,过点C作CH⊥y轴,过点 D作DG⊥BH,
∴∠DBG+∠GDB=90°,∠DBG+∠CBH=90°,∴∠GDB=∠CBH,
即 ∴BG=8,∴D(2,8);
如图2,当∠BCD=90°时,
过点 D作DK⊥y轴交于点K,同理,得△OBC∽△KCD,
即 ∴KC=4,∴D(2,-7);
综上所述,△BCD是以BC 为直角边的直角三角形时,D点坐标为(2,8)或(2,-7);
(3)如图3,过点A作AE⊥x轴交直线 BC于点 E,过 P作 PF⊥x轴交直线 BC 于点 F,
∴PF∥AE,
由点 B,C的坐标得,直线 BC 的表达式为
设 则
∵A(-2,0),∴E(-2,-4),∴AE=4,
∴当t=3时, 有最大值,此时,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末综合测试卷 (一)
时间: 60分钟 满分: 120分
一、选择题(共10小题,每小题3分,共30分)
1.已知一次函数y= ax+b经过点(-2,-3),正比例函数y = ax不经过第三象限,则反比例函数 的图象位于 ( )
A.第一、第二象限 B.第一、第三象限
C.第二、第三象限 D.第二、第四象限
2.笔、墨、纸、砚是中国传统的文房四宝,是中国书法的必备用具,如图是寓意“规矩方圆”的一方砚台,它的俯视图是( )
3.二次函数 (n为常数)的图象经过点, B(- ,y ),C(0,y ),则 y ,y ,y 的大小关系是 ( )
4.如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD 的度数是 ( )
A.110° B.115° C.120° D.125°
5.从1,2,3这三个数中任取两数,分别记为m,n,那么点(m,n)在反比例函数 图象上的概率为 ( )
B. C.
6.某停车场入口的栏杆如图所示,栏杆从水平位置AB 绕点O旋转到A'B'的位置,已知AO=4m,若栏杆的旋转角. 时,借助计算器求栏杆 A 端升高的高度,下列按键顺序正确的是 ( )
7.为解决停车问题,某小区在如图所示的一段道路边开辟一段斜列式停车位,每个车位长6m,宽2.4m,矩形停车位与道路成60°角,则在这一路段边上最多可以划出 个车位(参考数据: ( )
A.7 B.8 C.9 D.10
8.如图,在平面直角坐标系中,边长为2 的正六边形 ABCDEF 的中心与原点O重合,AB∥x轴,交y轴于点 P.将△OAP绕点O顺时针旋转,每次旋转90°,则第2 024次旋转结束时,点A 的坐标为 ( )
D.(1, )
第8题图 第9题图
9.如图,菱形ACBD中,AB与CD 交于O点, ,以C为圆心、AC为半径作弧AB,再以点C为圆心,CO为半径作弧EF,分别交AC于F 点,BC于E点,若CB=2,则图中阴影部分的面积为 ( )
10.如图,抛物线 与x轴交于点A,B,与y轴交于点C,对称轴为直线x=-1,若点A 的坐标为(--4,0),则下列结论正确的是 ( )
C.若关于x的一元二次方程 的两根为 则
D.点 在抛物线上,当 时
二、填空题(共6小题,每小题3分,共18分)
11.若代数式 有意义,则实数x的取值范围是 .
12.已知二次函数 当--3≤x≤2时,y的最大值为9,则k的值为 .
13.如图,在矩形ABCD中,点A,B在y轴上,BC∥x轴,对角线AC,BD交于点 E,BC=6,CD=3,反比例函数 经过C,E两点,则k的值为 .
第13题图 第14题图
14.如图,在Rt△ABC中, ,按下列步骤作图:①在AC和AB 上分别截取AD,AE,使AD=AE;②分别以点D和点E 为圆心,以大于 的长为半径作弧,两弧在∠BAC内交于点M;③作射线 AM交BC 于点 F.若点 P 是线段AF 上的一个动点,连接CP,则 的最小值是 .
15.如图,圆锥的侧面展开图是一个圆心角为 的扇形,若圆锥的底面圆半径是5,则圆锥的母线l为 .
第15题图 第16题图
16.在平面直角坐标系中,用12个含有 角的直角三角形拼成如图所示的图形,若 则图中与 位似的三角形直角顶点的坐标是 .
三、解答题(共8小题,共72分)
17.(6分)计算:
18.(7分)已知:如图,在平面直角坐标系中,一次函数. 与反比例函数 的图象交于点 A(2,m)和点 B,与x轴交于点 D.
(1)求m,a 及B 点坐标;
(2)根据图象直接写出不等式 的解集;
(3)若P 是x轴上一点,且满足 的面积等于5,求点 P 坐标.
19.(8分)为提升学生的核心素养,长沙市某教育教学联合体开展了城乡读书交流活动.该教育教学联合体的某成员校号召全体师生积极捐书.为了解所捐书的种类,校团委对部分书籍进行了随机抽样调查,所捐书籍分为四类:文学类(记作 A类),艺术类(记作B类),科普类(记作C类),其他类(记作D类).学生张华根据收集的数据绘制了如图1,图2所示的不完整的统计图,请根据统计图提供的信息,解答下列问题:
(1)本次随机抽样调查的书籍的本数是 本,并补全条形统计图;
(2)扇形统计图中B类所对应扇形的圆心角的度数是 °;
(3)小钟和小雅参与了本次捐书活动(两人各捐一本且两人各自捐书的种类是等可能的),请用列表或画树状图的方法,求他们捐的书是同类书的概率.
20.(8分)如图,四边形ABCD内接于⊙O,对角线AC,BD相交于点E,AC为⊙O的直径,
(1)求证:
(2)若⊙O的半径为- 求线段 DC的长.
21.(9分)某农户生产经销一种农产品,已知这种产品的成本价为每千克20元.市场调查发现,该产品每天的销售价为25(元/千克)时,每天销售量为30(千克).当产品的销售价每千克涨1元时每天销售量会减少2千克,设涨价x(元/千克)(x为正整数),每天销售量为y(千克).
(1)直接写出y与x之间的函数关系式;
(2)该农户想要每天获得128元的销售利润,销售价为多少
(3)每千克涨价多少元时,每天的销售利润最大 最大利润是多少元
22.(10分)如图,甲、乙两艘货轮同时从A港出发,分别向 B,D两港运送物资,最后到达A港正东方向的C港装运新的物资.甲货轮沿A港的东南方向航行40海里后到达B港,再沿北偏东 方向航行一定距离到达C港.乙货轮沿 A港的北偏东( 方向航行一定距离到达D港,再沿南偏东 方向航行一定距离到达 C港.(参考数据:
(1)求A,C两港之间的距离(结果保留小数点后一位);
(2)若甲、乙两艘货轮的速度相同(停靠B,D两港的时间相同),哪艘货轮先到达C港 请通过计算说明.
23.(11分)如图,在△ABC中,∠ACB=90°,D是BC中点.
(1)尺规作图:以AC为直径作⊙O,交AB于点E保留作图痕迹。不需写作法);
(2)求证:DE是⊙O的切线;
(3)若AC=8,AB=10,求O到CE的距离.
在,请求上点D的坐标;看不是我,将就将摊向。
(3)如图2、点P容重线BC下面称根据线上,连接AP变程于坐轴,每10
24.(13分)已知抛物线 与x轴交于 B(6,0)两点,与y轴交于点(
(1)求抛物线的表达式;
(2)如图1,在对称轴上是否存在点 D,使 是以 BC 为直角边的直角三角形 若存在,请求出点 D 的坐标;若不存在,请说明理由;
(3)如图2,点 P 在直线BC 下方的抛物线上,连接AP 交BC 于点M,当 最大时,请直接写出点 P 的坐标.
参考答案
1. D 2. C 3. B 4. A 5. B 6. A 7. D 8. D 9. A 10. C
17.解:
18.解:(1)∵函数y=x+1的图象经过点 A(2,m),∴m=3,∴A(2,3),
∵点A(2,3)在反比例函数图象上,∴a=6,∴反比例函数表达式为
联立,得 解得 或 ∴B(-3,-2);
(2)由图象,得不等式 的解集为x<-3或0
∴m+1=±2,∴m=1或-3,∴点 P 坐标为(-3,0)或(1,0).
19.解:(1)本次随机抽样调查的书籍的本数是40÷40%=100(本),
∴B 类 的本数是 100--25--40--15 =20(本),
故答案为:100,
补全条形统计图如图1:
(2)扇形统计图中 B类所对应扇形的圆心角的度数是
故答案为:72;
(3)画树状图如图2:
共有16种等可能的结果,其中小钟和小雅捐的书是同类书的结果有4种,
∴他们捐的书是同类书的概率为
20.解:(1)证明:设∠ACD=α,则∠BCA=2∠ACD=2α,∴∠ABD=∠ACD=α,
∵AC为⊙O的直径,∴∠ABC=90°,∴∠CBE=∠ABC-∠ABD=90°-α,
∴∠CBE=∠CEB,∴BC=CE;
(2)过点 C作CT⊥BE于T,如图所示:
∵⊙O的半径为 ,BC=4,∴AC=5,
设AD=x,由(1),得 BC=CE=4,
AC-CE=5-4=1,
∵∠BCE=∠ADE,∠BEC=∠AED,∴△BCE∽△ADE,
∴AD:BC=AE:BE,即x:4=1: BE,
∵AC为⊙O的直径,CT⊥BE,∴∠ADC=∠ETC=90°,
∴∠ECT=∠ACD,∴△ECT∽△ACD,
∴AD:ET=AC:CE,即 (负值舍去),
在Rt△ACD中,
由勾股定理得
21.解:(1)由题意得:y=30-2x,
∵30-2x>0,∴x<15,
∴y与x之间的函数关系式为y=30-2x(0
∵该农户想要每天获得128元的销售利润,
∴(x+5)(30-2x)=128,解得 (舍去),
∴销售价为25+11=36(元),
∴农户想要每天获得128元的销售利润,销售价为36元;
(3)w=(x+5)(30-2x)=-2(x-5) +200.
∵-2<0,∴当x=5时,w有最大值,最大值为200,
∴每千克涨价5元时,每天的销售利润最大,最大利润是200元.
22.解:(1)过点 B作BE⊥AC,垂足为 E,
在 Rt△ABE中, 40海里,
(海里), (海里),在 Rt△BCE中,∠CBE=60°,
(海里),
(海里),
∴A,C两港之间的距离约为77.2海里;
(2)甲货轮先到达C港,
理由:
由题意得∠CDF=30°,DF∥AG,∴∠GAD=∠ADF=60°,
∴∠ADC=∠ADF+∠CDF=90°,在 Rt△ACD 中, 30°,
海里,海里,
在 Rt△BCE中, 海里,海里),
∴甲货轮航行的路程=AB+BC=40+ 4(海里),
乙货轮航行的路程=AD+CD=10 105.4(海里),
∵96.4 海里<105.4海里,∴甲货轮先到达C港.
23.解:(1)如图,⊙O即为所求作;
(2)证明:如图,连接OE,CE,
∵AC为⊙O的直径,∴∠AEC=90°,∴∠CEB=90°,
∵D是BC中点,∴∠DCE=∠DEC,
∵OC=OE,∴∠OCE=∠OEC,
∴∠OED=∠OEC+∠DEC=∠OCE+∠DCE=∠ACB=90°,
∵OE是⊙O的半径,∴DE是⊙O的切线;
(3)如图,过点O作OF⊥CE于点F,∴F是CE 的中点,
∵O是AC 的中点,∴OF 是△ACE的中位线,
在△ABC中,∠ACB=90°,∵AC=8,AB=10,
∴10CE=8×6,∴CE=4.8,
∴OF=3.2,
∴O到CE 的距离为3.2.
24.解:(1)将点 A(-2,0),B(6,0),C(0,-3)代入 得
解得
(2)存在,理由:
如图1,当∠CBD=90°时,
过点 B作GH⊥x轴,过点C作CH⊥y轴,过点 D作DG⊥BH,
∴∠DBG+∠GDB=90°,∠DBG+∠CBH=90°,∴∠GDB=∠CBH,
即 ∴BG=8,∴D(2,8);
如图2,当∠BCD=90°时,
过点 D作DK⊥y轴交于点K,同理,得△OBC∽△KCD,
即 ∴KC=4,∴D(2,-7);
综上所述,△BCD是以BC 为直角边的直角三角形时,D点坐标为(2,8)或(2,-7);
(3)如图3,过点A作AE⊥x轴交直线 BC于点 E,过 P作 PF⊥x轴交直线 BC 于点 F,
∴PF∥AE,
由点 B,C的坐标得,直线 BC 的表达式为
设 则
∵A(-2,0),∴E(-2,-4),∴AE=4,
∴当t=3时, 有最大值,此时,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
