鲁教版九年级下册期末综合测试卷 (二)(含答案)
文档属性
| 名称 | 鲁教版九年级下册期末综合测试卷 (二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 11:34:43 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末综合测试卷 (二)
时间: 60分钟 满分: 120分
一、选择题(共10小题,每小题3分,共30分)
1.如图所示的这个几何体,下列图形不是这个几何体的三视图的是( )
第1题图 第2题图
2.在物理课上,同学们学习了“电学”知识之后,便可以设计一些简单的电路图.如图,小明设计了一个包含甲、乙两个开关组的电路图,如果在甲、乙这两个开关组中各闭合一个开关,那么小灯泡发亮的概率为 ( )
A. B. C. D.
3.如图,在同一平面直角坐标系中,一次函数y = kx+b(k,b是常数,且k≠0)与反比例函数 (c是常数,且c≠0)的图象相交于A(-3,-2),B(2,3)两点,则关于x的不等式 的解集是 ( )
或
4.如图,四边形 ABCD 内接于⊙O,BC∥AD,AC⊥BD.若∠AOD=120°,AD= 则∠CAO的度数与BC 的长分别为 ( )
A.10°,1 B.10°, C.15°,1
5.运用我们课本上采用的计算器进行计算时,下列说法不正确的是( )
A.计算 的按键顺序依次为
B.要打开计算器并启动其统计计算功能应按的键是
C.启动计算器的统计计算功能后,要清除原有统计数据应按键
D.用计算器计算时,依次按如下各键
最后显示结果是0.5
6.将抛物线 沿x轴向左平移4个单位长度后,得到的新抛物线的表达式为 ( )
7.如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点O,则 cos∠AOC的值等于 ( )
8.在数学跨学科主题活动课上,芳芳用半径15 cm,圆心角 的扇形纸板,做了一个圆锥形的生日帽,如图所示.在不考虑接缝的情况下,这个圆锥形生日帽的底面圆半径是 ( )
A.3cm B.4cm C.5cm D.6cm
9、如图是抛物线 的图象,其对称轴为. 且该图象与x轴的一个交点在点(-3,0)和(-4,0)之间,并经过点( 与点(1.5,y ),则下列结论:①abc>0 ②3a+c>0 ④对于任意实数m,都有 其中正确结论有 ( )
A.1个 B.2个 C.3个 D.4个
第9题图 第10题图
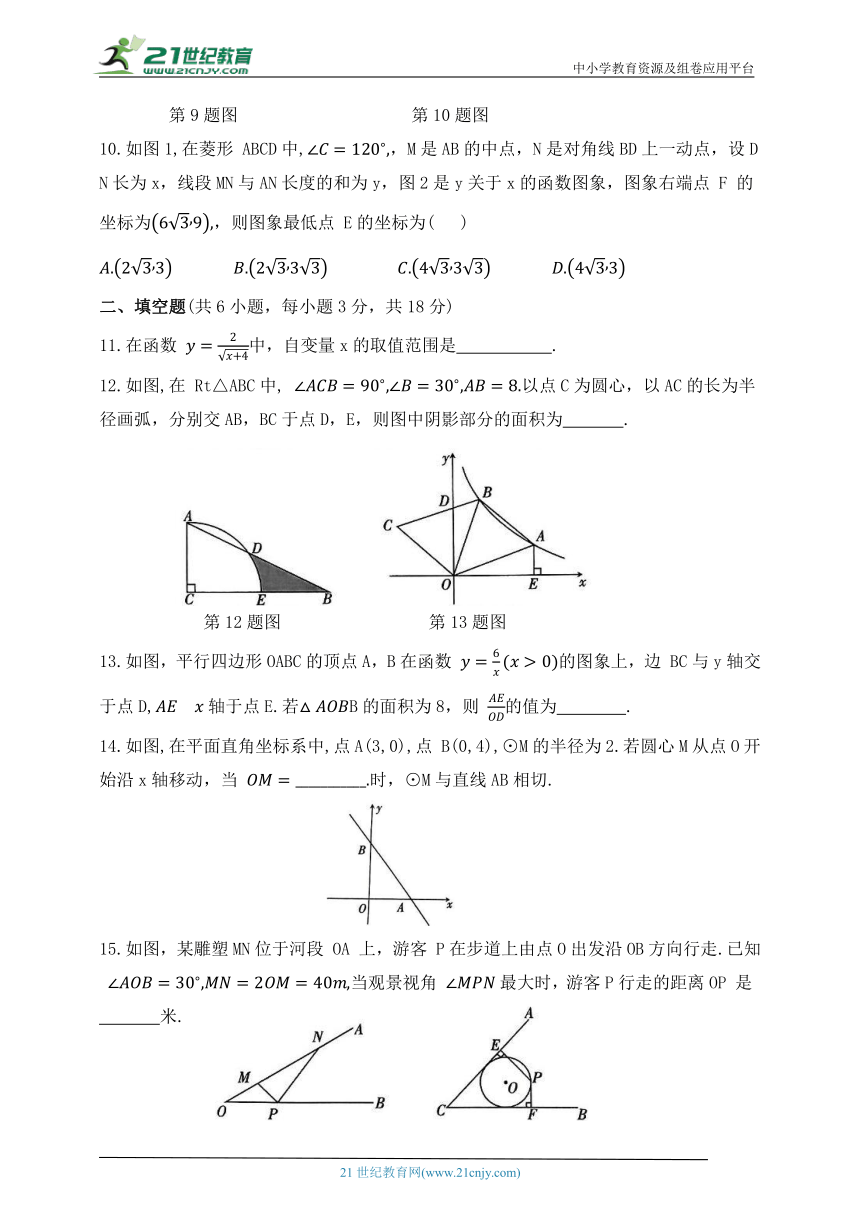
10.如图1,在菱形 ABCD中,,M是AB的中点,N是对角线BD上一动点,设DN长为x,线段MN与AN长度的和为y,图2是y关于x的函数图象,图象右端点 F 的坐标为,则图象最低点 E的坐标为( )
二、填空题(共6小题,每小题3分,共18分)
11.在函数 中,自变量x的取值范围是 .
12.如图,在 Rt△ABC中, 以点C为圆心,以AC的长为半径画弧,分别交AB,BC于点D,E,则图中阴影部分的面积为 .
第12题图 第13题图
13.如图,平行四边形OABC的顶点A,B在函数 的图象上,边 BC与y轴交于点D,轴于点E.若B的面积为8,则 的值为 .
14.如图,在平面直角坐标系中,点A(3,0),点 B(0,4),⊙M的半径为2.若圆心M从点O开始沿x轴移动,当 时,⊙M与直线AB相切.
15.如图,某雕塑MN位于河段 OA 上,游客 P在步道上由点O出发沿OB方向行走.已知 当观景视角 最大时,游客P行走的距离OP 是 米.
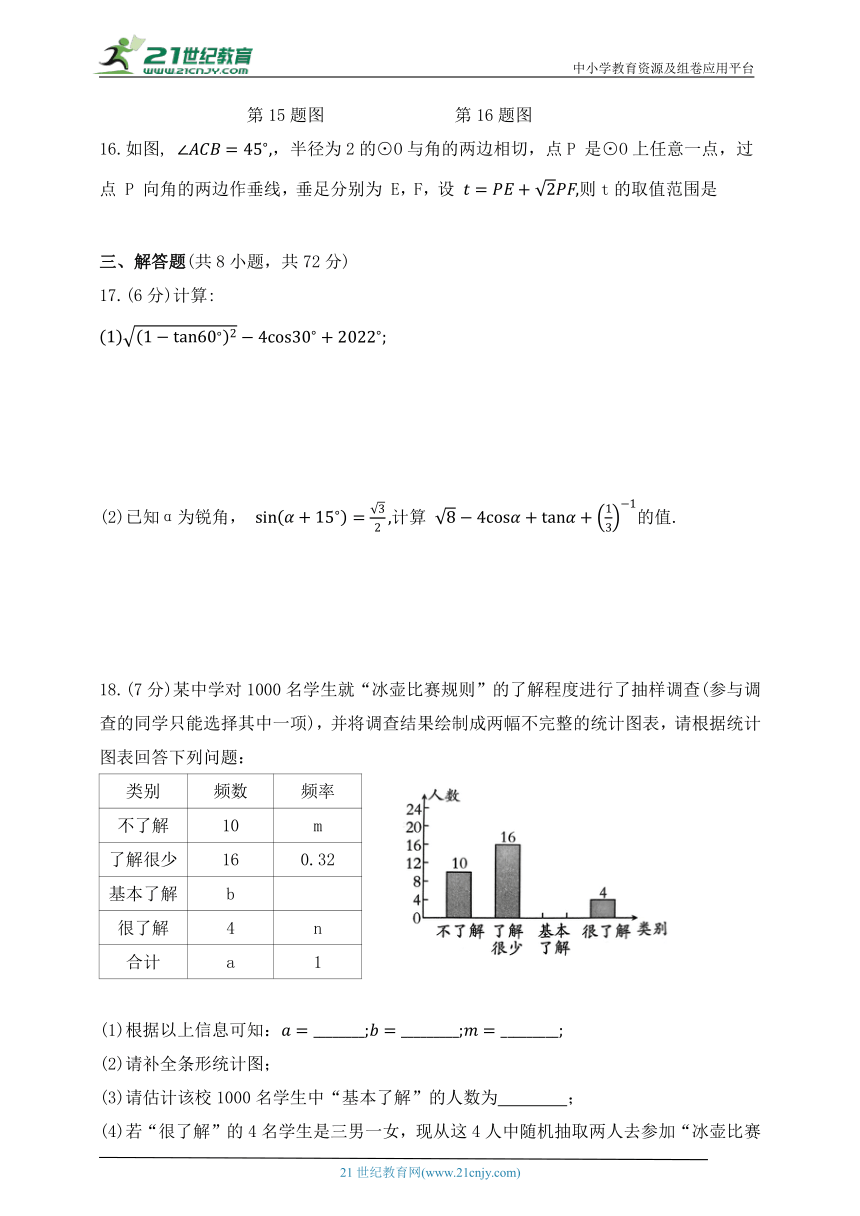
第15题图 第16题图
16.如图, ,半径为2的⊙O与角的两边相切,点P 是⊙O上任意一点,过点 P 向角的两边作垂线,垂足分别为 E,F,设 则t的取值范围是
三、解答题(共8小题,共72分)
17.(6分)计算:
(2)已知α为锐角, 计算 的值.
18.(7分)某中学对1000名学生就“冰壶比赛规则”的了解程度进行了抽样调查(参与调查的同学只能选择其中一项),并将调查结果绘制成两幅不完整的统计图表,请根据统计图表回答下列问题:
类别 频数 频率
不了解 10 m
了解很少 16 0.32
基本了解 b
很了解 4 n
合计 a 1
(1)根据以上信息可知:
(2)请补全条形统计图;
(3)请估计该校1000名学生中“基本了解”的人数为 ;
(4)若“很了解”的4名学生是三男一女,现从这4人中随机抽取两人去参加“冰壶比赛规则”知识竞赛,请用画树状图或列表的方法说明,抽到两名学生均为男生和抽到一男一女的概率是否相同.
19.(8分)如图,正比例函数 与反比例函数 的图象交于A,B两点,A的横坐标为 B的纵坐标为
(1)求反比例函数的表达式;
(2)观察图象,直接写出不等式 的解集;
(3)将直线AB向上平移n个单位,交双曲线于C,D两点,交坐标轴于点 E,F,连接OD,BD,若 的面积为20,求直线CD的表达式.
20.(8分)如图1,是一电动门,当它水平下落时,可以抽象成如图2所示的矩形ABCD,其中 ,此时它与出入口OM等宽,与地面的距离. 0.2m;当它抬起时,变为平行四边形. ,如图3所示,此时, 与水平方向的夹角为
(1)求点 到地面的距离;
(2)在电动门抬起的过程中,求点 C所经过的路径长;
(3)一辆高1.6m,宽1.5m 的汽车从该入口进入时,汽车需要与 BC保持0.4m 的安全距离,此时,汽车能否安全通过,若能,请通过计算说明;若不能,说明理由.(参考数据: 1.73,π≈3.14,月所有结果精确到0.1)
21.(9分)2023 春节档电影《满江红》热映,进一步激发观众爱国之情.南阳与名将岳飞有着一段传颂至今的历史——公元1138年,岳飞统军过南阳到武侯祠敬拜诸葛亮,雨夜含泪手书前后《出师表》,为南阳留下了千古绝唱“三绝碑”.
某超市采购了两批同样的《出师表》纪念品挂件,第一批花了3300元,第二批花了4000元,已知第一批每个挂件的进价是第二批的 1.1倍,且第二批比第一批多购进25个.
(1)求第二批每个挂件的进价;
(2)两批挂件售完后,该超市以第二批每个挂件的进价又采购一批同样的挂件,经市场调查发现,当售价为每个60元时,每周能卖出40个,若每降价1元,每周多卖10个,由于货源紧缺,每周最多能卖90个,求每个挂件售价定为多少元时,每周可获得最大利润,最大利润是多少
22.(10分)[2024·苏州市模拟]如图,以AB为直径的⊙O是 的外接圆,延长BC到点D.使得 点E在DA 的延长线上,点 M在线段AC 上,CE交BM 于点N,CE交AB 于点G.
(1)求证:ED是⊙O的切线;
(2)若 求 BC的长;
(3)若DE·AM=AC·AD,求证:
23.(11分)【情境探究】小明和小强做弹力球游戏.游戏规则如下:小明抛出弹力球,弹力球落地后弹起再落下,小强在某个位置放置一块接球板,若弹力球在第二次落地前碰到接球板则小强胜(球与接球板触碰),否则小明胜.
【数学建模】弹力球两次运动轨迹均可近似看成抛物线,如图所示.一次游戏过程中:小明站在起点O处抛弹力球,以O为坐标原点、水平方向直线和竖直方向直线分别为x轴和y轴建立平面直角坐标系,弹力球从离地面2米的A处抛出,第一次落地前,球在距离起点O水平距离为2m处,达到飞行最大高度为3.6m ,弹力球在 B处落地后再次弹起,第二次飞行的水平距离 BC=4米,且飞行的最大高度为第一次的一半.
【问题解决】
(1)求弹力球第一次着地前抛物线的函数表达式;
(2)小强在距起点8米处放置接球板EF,EF 垂直地面于点B,且 请通过计算判断谁会获胜.
24.(13分)如图1,抛物线 与x轴交于点A,与直线. 交于点 点 在y轴上.点P 从点 B 出发,沿线段 BO方向匀速运动,运动到点O时停止.
(1)求抛物线 的表达式;
(2)当时,请在图1中过点P作交抛物线于点D,连接PC,OD,判断四边形OCPD 的形状,并说明理由;
(3)如图2,点P 从点B 开始运动时,点Q从点O同时出发,以与点 P 相同的速度沿x轴正方向匀速运动,点P 停止运动时点Q 也停止运动.连接 BQ,PC,求 的最小值.
参考答案
1. B 2. B 3. C 4. C 5. D 6. A 7. B 8. C 9. C 10. C
11. x>-4
解析:如图所示,过点 D 作DG⊥AC于点G,连接CD,
∵∠ACB=90°,∠B=30°,AB=8,
∴∠BAC=60°,AC=AB·sinB=4,BC=
∵以AC的长为半径画弧,分别交AB,BC于点D,E,∴CA=CD=CE=4,
又∵∠BAC=60°,∴△ACD是等边三角形,
∴∠ACD=60°,∴∠ECD=30°,
在 Rt△CDG中,GD=CD·sin∠DCG=2
∴S阴影=S△ABC-S△ACD-S扇形CDE
13. 解析:连接AD,
∵四边形 OABC 是平行四边形,△AOB 的面积为8,∴S△AOD=8,
∵反比例函数y= ,AE⊥x轴,∴S△AOE=3,
又∵AE∥OD,
14. 或 解析:作OC⊥AB于点C,
∵A(3,0),点 B(0,4),∴OA=3,OB=4,
∵∠AOB=90°,
当点 M 在点 A 的左侧,设⊙M与直线AB相切于点 D,连接MD,则AB⊥MD,
∴∠ADM=∠AOB=90°,
∵∠DAM=∠OAB,∴△ADM∽△AOB,
当点 M'在点A 的右侧,设⊙M'与直线AB相切于点E,连接M'E,则 AB⊥M'E,
∵∠EAM'=∠DAM,EM'=DM,∴△AEM'≌△ADM(AAS),
∴当 或 时,⊙M 与直线AB 相切.
15.20 解析:如图,取 MN 的中点F,过点F作FE⊥OB于E,以直径MN作⊙F,
∵MN=2OM=40 m,点 F 是MN 的中点,∴MF=FN=20m,OF=40m,
∵∠AOB=30°,EF⊥OB,
∴EF=MF,即EF为⊙F半径,∴OB 是⊙F的切线,切点为 E,
∴当点 P 与点 E 重合时,观景视角∠MPN最大,此时
解析:设半径为2的⊙O与角的两边相切于M,N,连接OM,ON,延长NO交CB 于点 D,如图1,
∴∠CND=∠OMD=90°,
∵∠ACB=45°,∴△CND是等腰直角三角形,∴∠CDN=45°,
∵ON=OM=2,
如图1,延长EP 交 BC 于点Q,
∵EQ⊥AC,PF⊥BC,∴∠CEQ=∠PFQ=90°,
∵∠ACB=45°,∴∠EQC=45°,
∴△ECQ与△PFQ是等腰直角三角形,
当 EQ与⊙O相切且点 P 在圆心的右侧时,t有最大值,连接OP,如图2,
则四边形 ENOP 是正方形,∴EN=OP=2,
如图3,当 EQ与⊙O相切且点 P 在圆心的左侧时,t有最小值,
同理可得
故t的取值范围是
17.解:(1)原式
∴α=45°,
=4.
18.解:(1)a=16÷0.32=50,b=50-(10+16+4)=20,m=10÷50=0.2,n=4÷50=0.08;
(2)补全条形图如图所示:
(3)估计该校1 000名初中学生中“基本了解”的人数约有 (人),故答案为:400;
(4)记4名学生中3名男生分别为 A ,A ,A ,一名女生为B,列表如表所示:
第二次 第一次 A A A B
A — (A ,A ) (A ,A ) (A ,B)
A (A ,A ) --- (A ,A ) (A ,B)
A (A ,A ) (A ,A ) 一 (A ,B)
B (B,A ) (B,A ) (B,A ) 一
共有12个等可能的结果,抽到两名学生均为男生的有6种,
∴P(抽到两名学生均为男生) 抽到一男一女的有6种,
∴P(抽到一男一女)
故抽到两名学生均为男生和抽到一男一女的概率相同.
19.解:(1)∵正比例函数y= kx(k≠0)与反比例函数 的图象交于A,B两点,∴A,B关于原点对称,
∵A的横坐标为-4,B的纵坐标为-6,∴A(-4,6),B(4,-6),
∵点A(-4,6)在反比例函数 0)的图象上,
∴m=-24,∴反比例函数的表达式为
(2)观察函数图象,得当-44时,正比例函数y=kx的图象在反比例函数 的图象下方,∴不等式 的解集为-44;
(3)方法一:连接 BE,作 BG⊥y轴于点G,
∵A(-4,6)在直线y= kx上,∴6=-4k,解得
∴直线 AB的表达式为
∵CD∥AB,
∵B(4,-6),∴BG=4,
∴OE=10,∴E(0,10),∴直线CD为
方法二:
连接BF,作 BH⊥x轴于点 H,
∵A(-4,6)在直线y= kx上,∴直线 AB的表达式为
∵CD∥AB,
∵B(4,-6),
设直线CD的表达式为 代入F点的坐标,得 解得b=10,∴直线CD为
20.解:(1)如图,过点 B'作 B'N⊥OM 于点 N,交AB于点E,
∴B'N=B'E+EN=2.6+0.2=2.8(m);
(2)∵点C'是点C 绕点 D 旋转60°得到,∴点 C 经过的路径长为 3.1(m);
(3)在OM上取MK=0.4m ,KF=1.5m ,作 FG⊥OM于点 F,交 AB 于点 H,交 AB'于点G,当汽车与BC保持安全距离0.4m时,
∵汽车宽为1.5m,∴OF=3-1.5-0.4=1.1(m),
∵AB∥OM,AO⊥OM,GF⊥OM,∴AH=OF=1. 1m,∠AHG=90°,HF=OA=0.2m,
∵GH+HF=1.903+0.2≈2.1m >1.6m,∴汽车能安全通过.
21.解:(1)设第二批每个挂件进价是每个x元,根据题意得
解得x=40,经检验,x=40是原方程的解,也符合题意,∴x=40,
答:第二批每个挂件进价是每个40元;
(2)设每个挂件售价定为 m元,每周可获得利润W 元,
∵每周最多能卖90个,解得m≥55,
根据题意得 -10(m-52) +1440,
∵--10<0,∴当m≥52时,W 随m的增大而减小,
∵m≥55,∴当m=55时,W 取最大,此时W=-10×(55-52) +1440=1350.
∴当每个挂件售价定为55元时,每周可获得最大利润,最大利润是1350元.
22.解:(1)证明:∵AB是⊙O的直径,∴∠BAC+∠ABC=90°,
∵∠BAC=∠BDA,∴∠BDA+∠ABC=90°,∴∠BAD=90°,∴ED 是⊙O的切线:
(2)∵∠BAC=∠BDA,∠ACB=∠DCA=90°、∴△ACB∽△DCA,
解得 BC=2或BC=3.
当BC 2时,CD=BD~BC=3,
当BC=3时CD=BD-BC=2,
∵AC>CD,即 ∴BC=3;
(3)证明:由(2),得△ABC∽△DAC,AC= ∴AC·AD=CD·AB,
∵DE·AM=AC·AD,∴DE·AM=CD·AB,
又∵∠BAM=∠CDE,∴△AMB∽△DCE,∴∠E=∠ABM,
∵∠EGA=∠BGN,∠BAD=90°,∴∠EGA+∠E=∠ABM+∠BGN=90°,∴∠BNG=90°,
∴BM⊥CE.
23.解:(1)由题意得弹力球第一次着地前抛物线的函数表达式的顶点坐标为(2,3.6).
设弹力球第一次着地前抛物线的函数表达式为
∵经过点A(0,2),∴2=a(0-2) +3.6.解得a=-0.4.
∴弹力球第一次着地前抛物线的函数表达式为
(2)小明获胜.理由:
当y=0时,0=-0.4(x-2) +3.6.解得. (不合题意,舍去),x =5.
∴点 B的坐标为(5,0).
∵BC=4,∴点 C的坐标为(9,0).
∵第二次飞行的最大高度为第一次的一半.
∴弹力球第二次飞行时抛物线的顶点坐标为(7,1.8).
∴设弹力球第二次飞行时抛物线的函数表达式为y=m(x-7) +1.8.
∵经过点 B(5,0),∴0=m(5-7) +1.8.解得m=-0.45.
∴弹力球第二次飞行时抛物线的函数表达式为y=-0.45(x-7) +1.8.
当x=8时,y=-0.45×(8-7) +1.8=1.35.∵1.35>1,
∴球与接球板不碰撞.∴小明获胜.
24.解:(1)∵抛物线 过点 B(4,-4),∴--16+46=-4.∴b=3.
即抛物线的表达式为
(2)四边形OCPD是平行四边形,理由:
如图1,作 PD⊥OA 交x 轴于点 H,连接PC,OD,
∵点 P 在y=-x上,∴OH=PH,∠POH=45°,连接BC,
∵C(0,-4),B(4,-4),∴OC=BC=4,CB⊥y轴,
当xD=2时,DH=yD=-4+3×2=2,∴PD=DH+PH=2+2=4,
∵C(0,-4),∴OC=4,∴PD=OC,
∵OC⊥x轴,PD⊥x轴,∴PD∥OC,∴四边形OCPD是平行四边形;
(3)如图2,由题意,得 BP=OQ,连接 BC,
在OA 上方作△OMQ,使得∠MOQ=45°,OM=BC=4,
∵BC⊥OC,∠BCO=45°,∴∠CBP=45°,∴∠CBP=∠MOQ,
∵BP=OQ,∠CBP=∠MOQ,BC=OM,∴△CBP≌△MOQ(SAS),∴CP=MQ,
∴CP+BQ=MQ+BQ≥MB,当M,Q,B三点共线时,CP+BQ取得最小值为MB,
∵∠MOB=∠MOQ+∠BOQ=45°+45°=90°, 即CP+BQ的最小值为4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末综合测试卷 (二)
时间: 60分钟 满分: 120分
一、选择题(共10小题,每小题3分,共30分)
1.如图所示的这个几何体,下列图形不是这个几何体的三视图的是( )
第1题图 第2题图
2.在物理课上,同学们学习了“电学”知识之后,便可以设计一些简单的电路图.如图,小明设计了一个包含甲、乙两个开关组的电路图,如果在甲、乙这两个开关组中各闭合一个开关,那么小灯泡发亮的概率为 ( )
A. B. C. D.
3.如图,在同一平面直角坐标系中,一次函数y = kx+b(k,b是常数,且k≠0)与反比例函数 (c是常数,且c≠0)的图象相交于A(-3,-2),B(2,3)两点,则关于x的不等式 的解集是 ( )
或
4.如图,四边形 ABCD 内接于⊙O,BC∥AD,AC⊥BD.若∠AOD=120°,AD= 则∠CAO的度数与BC 的长分别为 ( )
A.10°,1 B.10°, C.15°,1
5.运用我们课本上采用的计算器进行计算时,下列说法不正确的是( )
A.计算 的按键顺序依次为
B.要打开计算器并启动其统计计算功能应按的键是
C.启动计算器的统计计算功能后,要清除原有统计数据应按键
D.用计算器计算时,依次按如下各键
最后显示结果是0.5
6.将抛物线 沿x轴向左平移4个单位长度后,得到的新抛物线的表达式为 ( )
7.如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点O,则 cos∠AOC的值等于 ( )
8.在数学跨学科主题活动课上,芳芳用半径15 cm,圆心角 的扇形纸板,做了一个圆锥形的生日帽,如图所示.在不考虑接缝的情况下,这个圆锥形生日帽的底面圆半径是 ( )
A.3cm B.4cm C.5cm D.6cm
9、如图是抛物线 的图象,其对称轴为. 且该图象与x轴的一个交点在点(-3,0)和(-4,0)之间,并经过点( 与点(1.5,y ),则下列结论:①abc>0 ②3a+c>0 ④对于任意实数m,都有 其中正确结论有 ( )
A.1个 B.2个 C.3个 D.4个
第9题图 第10题图
10.如图1,在菱形 ABCD中,,M是AB的中点,N是对角线BD上一动点,设DN长为x,线段MN与AN长度的和为y,图2是y关于x的函数图象,图象右端点 F 的坐标为,则图象最低点 E的坐标为( )
二、填空题(共6小题,每小题3分,共18分)
11.在函数 中,自变量x的取值范围是 .
12.如图,在 Rt△ABC中, 以点C为圆心,以AC的长为半径画弧,分别交AB,BC于点D,E,则图中阴影部分的面积为 .
第12题图 第13题图
13.如图,平行四边形OABC的顶点A,B在函数 的图象上,边 BC与y轴交于点D,轴于点E.若B的面积为8,则 的值为 .
14.如图,在平面直角坐标系中,点A(3,0),点 B(0,4),⊙M的半径为2.若圆心M从点O开始沿x轴移动,当 时,⊙M与直线AB相切.
15.如图,某雕塑MN位于河段 OA 上,游客 P在步道上由点O出发沿OB方向行走.已知 当观景视角 最大时,游客P行走的距离OP 是 米.
第15题图 第16题图
16.如图, ,半径为2的⊙O与角的两边相切,点P 是⊙O上任意一点,过点 P 向角的两边作垂线,垂足分别为 E,F,设 则t的取值范围是
三、解答题(共8小题,共72分)
17.(6分)计算:
(2)已知α为锐角, 计算 的值.
18.(7分)某中学对1000名学生就“冰壶比赛规则”的了解程度进行了抽样调查(参与调查的同学只能选择其中一项),并将调查结果绘制成两幅不完整的统计图表,请根据统计图表回答下列问题:
类别 频数 频率
不了解 10 m
了解很少 16 0.32
基本了解 b
很了解 4 n
合计 a 1
(1)根据以上信息可知:
(2)请补全条形统计图;
(3)请估计该校1000名学生中“基本了解”的人数为 ;
(4)若“很了解”的4名学生是三男一女,现从这4人中随机抽取两人去参加“冰壶比赛规则”知识竞赛,请用画树状图或列表的方法说明,抽到两名学生均为男生和抽到一男一女的概率是否相同.
19.(8分)如图,正比例函数 与反比例函数 的图象交于A,B两点,A的横坐标为 B的纵坐标为
(1)求反比例函数的表达式;
(2)观察图象,直接写出不等式 的解集;
(3)将直线AB向上平移n个单位,交双曲线于C,D两点,交坐标轴于点 E,F,连接OD,BD,若 的面积为20,求直线CD的表达式.
20.(8分)如图1,是一电动门,当它水平下落时,可以抽象成如图2所示的矩形ABCD,其中 ,此时它与出入口OM等宽,与地面的距离. 0.2m;当它抬起时,变为平行四边形. ,如图3所示,此时, 与水平方向的夹角为
(1)求点 到地面的距离;
(2)在电动门抬起的过程中,求点 C所经过的路径长;
(3)一辆高1.6m,宽1.5m 的汽车从该入口进入时,汽车需要与 BC保持0.4m 的安全距离,此时,汽车能否安全通过,若能,请通过计算说明;若不能,说明理由.(参考数据: 1.73,π≈3.14,月所有结果精确到0.1)
21.(9分)2023 春节档电影《满江红》热映,进一步激发观众爱国之情.南阳与名将岳飞有着一段传颂至今的历史——公元1138年,岳飞统军过南阳到武侯祠敬拜诸葛亮,雨夜含泪手书前后《出师表》,为南阳留下了千古绝唱“三绝碑”.
某超市采购了两批同样的《出师表》纪念品挂件,第一批花了3300元,第二批花了4000元,已知第一批每个挂件的进价是第二批的 1.1倍,且第二批比第一批多购进25个.
(1)求第二批每个挂件的进价;
(2)两批挂件售完后,该超市以第二批每个挂件的进价又采购一批同样的挂件,经市场调查发现,当售价为每个60元时,每周能卖出40个,若每降价1元,每周多卖10个,由于货源紧缺,每周最多能卖90个,求每个挂件售价定为多少元时,每周可获得最大利润,最大利润是多少
22.(10分)[2024·苏州市模拟]如图,以AB为直径的⊙O是 的外接圆,延长BC到点D.使得 点E在DA 的延长线上,点 M在线段AC 上,CE交BM 于点N,CE交AB 于点G.
(1)求证:ED是⊙O的切线;
(2)若 求 BC的长;
(3)若DE·AM=AC·AD,求证:
23.(11分)【情境探究】小明和小强做弹力球游戏.游戏规则如下:小明抛出弹力球,弹力球落地后弹起再落下,小强在某个位置放置一块接球板,若弹力球在第二次落地前碰到接球板则小强胜(球与接球板触碰),否则小明胜.
【数学建模】弹力球两次运动轨迹均可近似看成抛物线,如图所示.一次游戏过程中:小明站在起点O处抛弹力球,以O为坐标原点、水平方向直线和竖直方向直线分别为x轴和y轴建立平面直角坐标系,弹力球从离地面2米的A处抛出,第一次落地前,球在距离起点O水平距离为2m处,达到飞行最大高度为3.6m ,弹力球在 B处落地后再次弹起,第二次飞行的水平距离 BC=4米,且飞行的最大高度为第一次的一半.
【问题解决】
(1)求弹力球第一次着地前抛物线的函数表达式;
(2)小强在距起点8米处放置接球板EF,EF 垂直地面于点B,且 请通过计算判断谁会获胜.
24.(13分)如图1,抛物线 与x轴交于点A,与直线. 交于点 点 在y轴上.点P 从点 B 出发,沿线段 BO方向匀速运动,运动到点O时停止.
(1)求抛物线 的表达式;
(2)当时,请在图1中过点P作交抛物线于点D,连接PC,OD,判断四边形OCPD 的形状,并说明理由;
(3)如图2,点P 从点B 开始运动时,点Q从点O同时出发,以与点 P 相同的速度沿x轴正方向匀速运动,点P 停止运动时点Q 也停止运动.连接 BQ,PC,求 的最小值.
参考答案
1. B 2. B 3. C 4. C 5. D 6. A 7. B 8. C 9. C 10. C
11. x>-4
解析:如图所示,过点 D 作DG⊥AC于点G,连接CD,
∵∠ACB=90°,∠B=30°,AB=8,
∴∠BAC=60°,AC=AB·sinB=4,BC=
∵以AC的长为半径画弧,分别交AB,BC于点D,E,∴CA=CD=CE=4,
又∵∠BAC=60°,∴△ACD是等边三角形,
∴∠ACD=60°,∴∠ECD=30°,
在 Rt△CDG中,GD=CD·sin∠DCG=2
∴S阴影=S△ABC-S△ACD-S扇形CDE
13. 解析:连接AD,
∵四边形 OABC 是平行四边形,△AOB 的面积为8,∴S△AOD=8,
∵反比例函数y= ,AE⊥x轴,∴S△AOE=3,
又∵AE∥OD,
14. 或 解析:作OC⊥AB于点C,
∵A(3,0),点 B(0,4),∴OA=3,OB=4,
∵∠AOB=90°,
当点 M 在点 A 的左侧,设⊙M与直线AB相切于点 D,连接MD,则AB⊥MD,
∴∠ADM=∠AOB=90°,
∵∠DAM=∠OAB,∴△ADM∽△AOB,
当点 M'在点A 的右侧,设⊙M'与直线AB相切于点E,连接M'E,则 AB⊥M'E,
∵∠EAM'=∠DAM,EM'=DM,∴△AEM'≌△ADM(AAS),
∴当 或 时,⊙M 与直线AB 相切.
15.20 解析:如图,取 MN 的中点F,过点F作FE⊥OB于E,以直径MN作⊙F,
∵MN=2OM=40 m,点 F 是MN 的中点,∴MF=FN=20m,OF=40m,
∵∠AOB=30°,EF⊥OB,
∴EF=MF,即EF为⊙F半径,∴OB 是⊙F的切线,切点为 E,
∴当点 P 与点 E 重合时,观景视角∠MPN最大,此时
解析:设半径为2的⊙O与角的两边相切于M,N,连接OM,ON,延长NO交CB 于点 D,如图1,
∴∠CND=∠OMD=90°,
∵∠ACB=45°,∴△CND是等腰直角三角形,∴∠CDN=45°,
∵ON=OM=2,
如图1,延长EP 交 BC 于点Q,
∵EQ⊥AC,PF⊥BC,∴∠CEQ=∠PFQ=90°,
∵∠ACB=45°,∴∠EQC=45°,
∴△ECQ与△PFQ是等腰直角三角形,
当 EQ与⊙O相切且点 P 在圆心的右侧时,t有最大值,连接OP,如图2,
则四边形 ENOP 是正方形,∴EN=OP=2,
如图3,当 EQ与⊙O相切且点 P 在圆心的左侧时,t有最小值,
同理可得
故t的取值范围是
17.解:(1)原式
∴α=45°,
=4.
18.解:(1)a=16÷0.32=50,b=50-(10+16+4)=20,m=10÷50=0.2,n=4÷50=0.08;
(2)补全条形图如图所示:
(3)估计该校1 000名初中学生中“基本了解”的人数约有 (人),故答案为:400;
(4)记4名学生中3名男生分别为 A ,A ,A ,一名女生为B,列表如表所示:
第二次 第一次 A A A B
A — (A ,A ) (A ,A ) (A ,B)
A (A ,A ) --- (A ,A ) (A ,B)
A (A ,A ) (A ,A ) 一 (A ,B)
B (B,A ) (B,A ) (B,A ) 一
共有12个等可能的结果,抽到两名学生均为男生的有6种,
∴P(抽到两名学生均为男生) 抽到一男一女的有6种,
∴P(抽到一男一女)
故抽到两名学生均为男生和抽到一男一女的概率相同.
19.解:(1)∵正比例函数y= kx(k≠0)与反比例函数 的图象交于A,B两点,∴A,B关于原点对称,
∵A的横坐标为-4,B的纵坐标为-6,∴A(-4,6),B(4,-6),
∵点A(-4,6)在反比例函数 0)的图象上,
∴m=-24,∴反比例函数的表达式为
(2)观察函数图象,得当-4
(3)方法一:连接 BE,作 BG⊥y轴于点G,
∵A(-4,6)在直线y= kx上,∴6=-4k,解得
∴直线 AB的表达式为
∵CD∥AB,
∵B(4,-6),∴BG=4,
∴OE=10,∴E(0,10),∴直线CD为
方法二:
连接BF,作 BH⊥x轴于点 H,
∵A(-4,6)在直线y= kx上,∴直线 AB的表达式为
∵CD∥AB,
∵B(4,-6),
设直线CD的表达式为 代入F点的坐标,得 解得b=10,∴直线CD为
20.解:(1)如图,过点 B'作 B'N⊥OM 于点 N,交AB于点E,
∴B'N=B'E+EN=2.6+0.2=2.8(m);
(2)∵点C'是点C 绕点 D 旋转60°得到,∴点 C 经过的路径长为 3.1(m);
(3)在OM上取MK=0.4m ,KF=1.5m ,作 FG⊥OM于点 F,交 AB 于点 H,交 AB'于点G,当汽车与BC保持安全距离0.4m时,
∵汽车宽为1.5m,∴OF=3-1.5-0.4=1.1(m),
∵AB∥OM,AO⊥OM,GF⊥OM,∴AH=OF=1. 1m,∠AHG=90°,HF=OA=0.2m,
∵GH+HF=1.903+0.2≈2.1m >1.6m,∴汽车能安全通过.
21.解:(1)设第二批每个挂件进价是每个x元,根据题意得
解得x=40,经检验,x=40是原方程的解,也符合题意,∴x=40,
答:第二批每个挂件进价是每个40元;
(2)设每个挂件售价定为 m元,每周可获得利润W 元,
∵每周最多能卖90个,解得m≥55,
根据题意得 -10(m-52) +1440,
∵--10<0,∴当m≥52时,W 随m的增大而减小,
∵m≥55,∴当m=55时,W 取最大,此时W=-10×(55-52) +1440=1350.
∴当每个挂件售价定为55元时,每周可获得最大利润,最大利润是1350元.
22.解:(1)证明:∵AB是⊙O的直径,∴∠BAC+∠ABC=90°,
∵∠BAC=∠BDA,∴∠BDA+∠ABC=90°,∴∠BAD=90°,∴ED 是⊙O的切线:
(2)∵∠BAC=∠BDA,∠ACB=∠DCA=90°、∴△ACB∽△DCA,
解得 BC=2或BC=3.
当BC 2时,CD=BD~BC=3,
当BC=3时CD=BD-BC=2,
∵AC>CD,即 ∴BC=3;
(3)证明:由(2),得△ABC∽△DAC,AC= ∴AC·AD=CD·AB,
∵DE·AM=AC·AD,∴DE·AM=CD·AB,
又∵∠BAM=∠CDE,∴△AMB∽△DCE,∴∠E=∠ABM,
∵∠EGA=∠BGN,∠BAD=90°,∴∠EGA+∠E=∠ABM+∠BGN=90°,∴∠BNG=90°,
∴BM⊥CE.
23.解:(1)由题意得弹力球第一次着地前抛物线的函数表达式的顶点坐标为(2,3.6).
设弹力球第一次着地前抛物线的函数表达式为
∵经过点A(0,2),∴2=a(0-2) +3.6.解得a=-0.4.
∴弹力球第一次着地前抛物线的函数表达式为
(2)小明获胜.理由:
当y=0时,0=-0.4(x-2) +3.6.解得. (不合题意,舍去),x =5.
∴点 B的坐标为(5,0).
∵BC=4,∴点 C的坐标为(9,0).
∵第二次飞行的最大高度为第一次的一半.
∴弹力球第二次飞行时抛物线的顶点坐标为(7,1.8).
∴设弹力球第二次飞行时抛物线的函数表达式为y=m(x-7) +1.8.
∵经过点 B(5,0),∴0=m(5-7) +1.8.解得m=-0.45.
∴弹力球第二次飞行时抛物线的函数表达式为y=-0.45(x-7) +1.8.
当x=8时,y=-0.45×(8-7) +1.8=1.35.∵1.35>1,
∴球与接球板不碰撞.∴小明获胜.
24.解:(1)∵抛物线 过点 B(4,-4),∴--16+46=-4.∴b=3.
即抛物线的表达式为
(2)四边形OCPD是平行四边形,理由:
如图1,作 PD⊥OA 交x 轴于点 H,连接PC,OD,
∵点 P 在y=-x上,∴OH=PH,∠POH=45°,连接BC,
∵C(0,-4),B(4,-4),∴OC=BC=4,CB⊥y轴,
当xD=2时,DH=yD=-4+3×2=2,∴PD=DH+PH=2+2=4,
∵C(0,-4),∴OC=4,∴PD=OC,
∵OC⊥x轴,PD⊥x轴,∴PD∥OC,∴四边形OCPD是平行四边形;
(3)如图2,由题意,得 BP=OQ,连接 BC,
在OA 上方作△OMQ,使得∠MOQ=45°,OM=BC=4,
∵BC⊥OC,∠BCO=45°,∴∠CBP=45°,∴∠CBP=∠MOQ,
∵BP=OQ,∠CBP=∠MOQ,BC=OM,∴△CBP≌△MOQ(SAS),∴CP=MQ,
∴CP+BQ=MQ+BQ≥MB,当M,Q,B三点共线时,CP+BQ取得最小值为MB,
∵∠MOB=∠MOQ+∠BOQ=45°+45°=90°, 即CP+BQ的最小值为4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
