2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算专题训练(含解析)
文档属性
| 名称 | 2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算专题训练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算专题训练
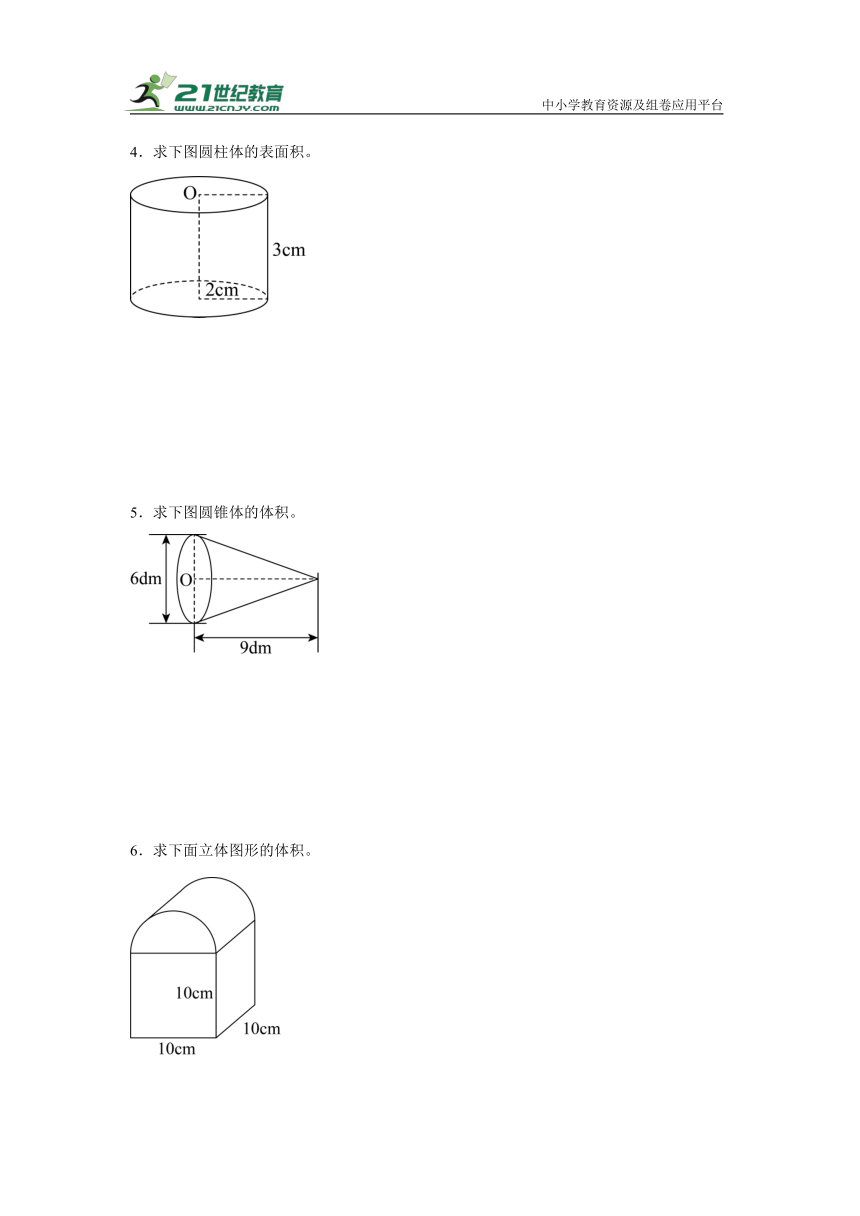
1.第一个图(单位:cm)求表面积,第二个图求体积。
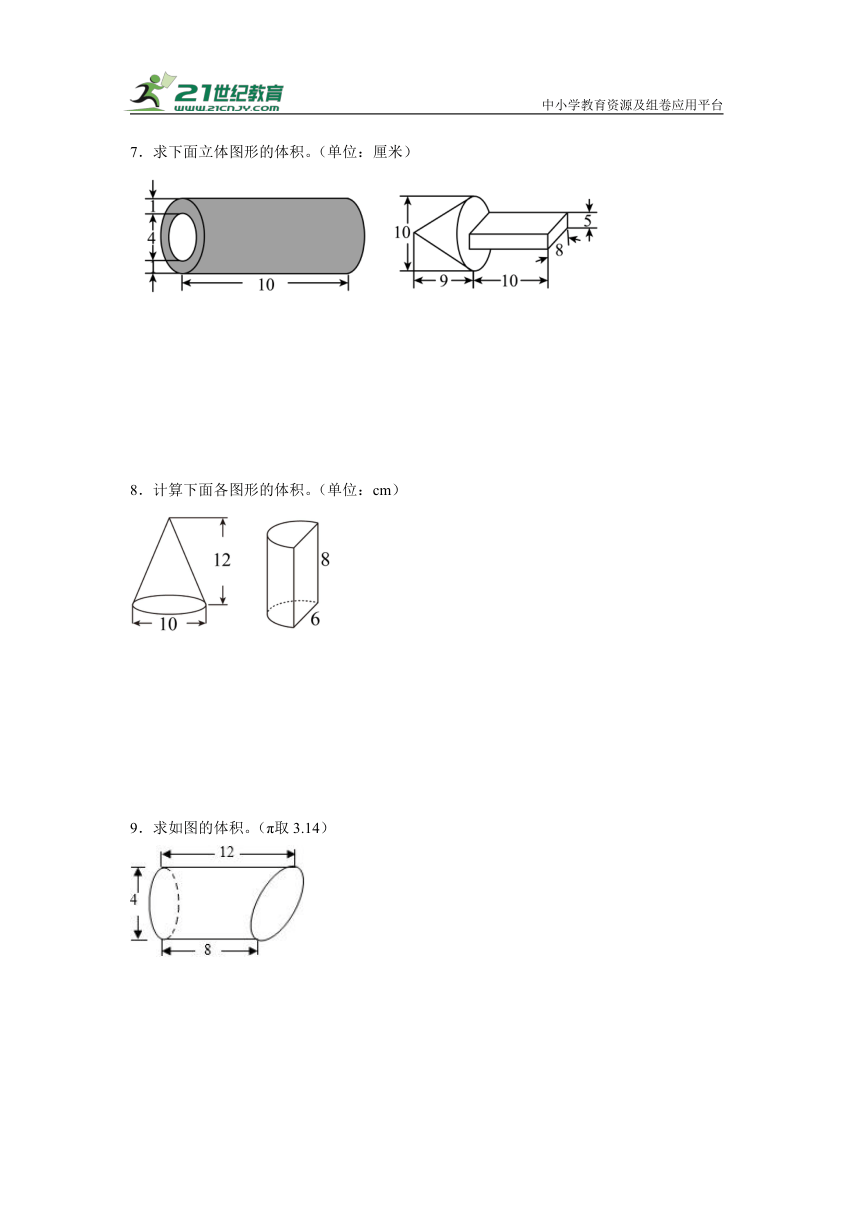
2.下面是圆柱的平面展开图,计算它的体积。(单位:厘米)
3.求下图立体图形的表面积。(单位:厘米)
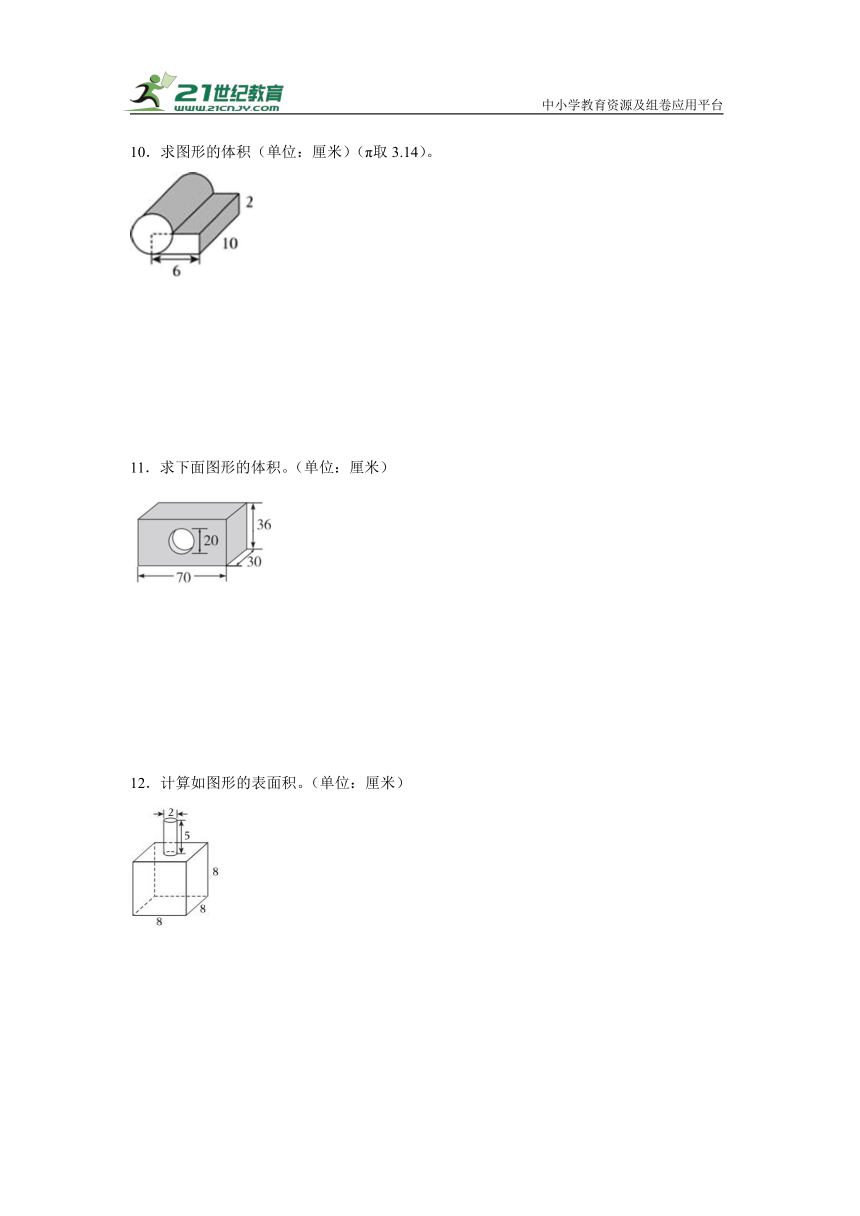
4.求下图圆柱体的表面积。
5.求下图圆锥体的体积。
6.求下面立体图形的体积。
7.求下面立体图形的体积。(单位:厘米)
8.计算下面各图形的体积。(单位:cm)
9.求如图的体积。(π取3.14)
10.求图形的体积(单位:厘米)(π取3.14)。
11.求下面图形的体积。(单位:厘米)
12.计算如图形的表面积。(单位:厘米)
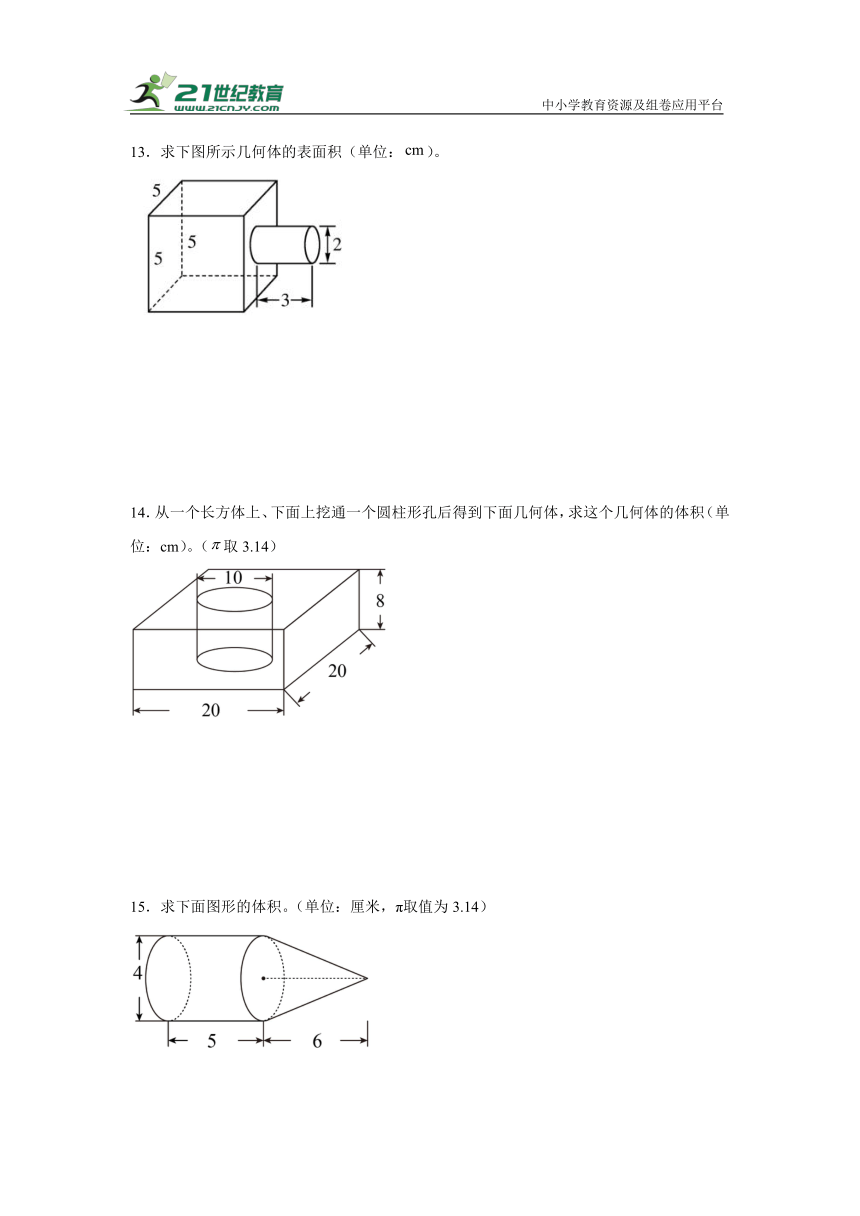
13.求下图所示几何体的表面积(单位:)。
14.从一个长方体上、下面上挖通一个圆柱形孔后得到下面几何体,求这个几何体的体积(单位:cm)。(取3.14)
15.求下面图形的体积。(单位:厘米,π取值为3.14)
16.求体积。
17.如图下图,求组合体的表面积。(单位:厘米;π取3.14)
18.计算下面各图形的体积。
19.求下面圆柱的表面积。
20.求如图所示图形的体积。(单位:cm)
21.求下面图形的体积。(左图中的半圆柱的底面直径是10厘米,右图是从圆柱中挖法一个圆锥后的剩余部分)。(单位:厘米)
22.计算下面图形的体积。(单位:米)
23.求下面图形的表面积。
24.求下面图形的表面积。(单位:厘米)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算专题训练》参考答案
1.(1)785cm2;(2)15.7cm3
【分析】(1)根据圆柱的表面积S表=S侧+2S底,其中S侧=πdh,S底=πr2,代入数据计算,即可求出圆柱的表面积。
(2)组合体的体积=圆柱的体积+圆锥的体积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算求解。
【详解】(1)3.14×10×20+3.14×(10÷2)2×2
=3.14×10×20+3.14×52×2
=628+3.14×25×2
=628+157
=785(cm2)
圆柱的表面积是785cm2。
(2)3.14×(2÷2)2×4+×3.14×(2÷2)2×3
=3.14×12×4+×3.14×12×3
=3.14×1×4+×3.14×1×3
=12.56+3.14
=15.7(cm3)
组合体的体积是15.7cm3。
2.141.3立方厘米
【分析】从圆柱的展开图中可知,圆柱的底面周长是18.84厘米,高是5厘米;先根据圆的周长公式C=2πr,可知r=C÷π÷2,由此求出圆柱的底面半径;再根据圆柱的体积公式V=πr2h,求出圆柱的体积。
【详解】底面半径:
18.84÷3.14÷2
=6÷2
=3(厘米)
体积:
3.14×32×5
=3.14×9×5
=141.3(立方厘米)
它的体积是141.3立方厘米。
3.228.8平方厘米
【分析】观察图形可知,圆柱和长方体有重合的部分,把圆柱的上底面向下平移,补给长方体的上面;这样长方体的表面积是6个面的面积之和,而圆柱只需计算侧面积即可;
图形的表面积=圆柱的侧面积+长方体的表面积
其中,圆柱的侧面积S侧=πdh,长方体的表面积S=2(ab+ah+bh),代入数据计算求解。
【详解】圆柱的侧面积:
3.14×4×5=62.8(平方厘米)
长方体的表面积:
(7×4+7×5+4×5)×2
=(28+35+20)×2
=83×2
=166(平方厘米)
组合体的表面积:
62.8+166=228.8(平方厘米)
图形的表面积是228.8平方厘米。
4.62.8cm2
【分析】从图中可知,圆柱的底面半径是2cm,高是3cm,根据圆柱的表面积公式S表=S侧+2S底,其中S侧=2πrh,S底=πr2,代入数据计算,即可求出这个圆柱的表面积。
【详解】2×3.14×2×3+3.14×22×2
=2×3.14×2×3+3.14×4×2
=37.68+25.12
=62.8(cm2)
圆柱体的表面积是62.8cm2。
5.84.78dm3
【分析】已知圆锥的底面直径是6dm,高是9dm,根据圆锥的体积公式V=πr2h,代入数据计算求出圆锥的体积。
【详解】×3.14×(6÷2)2×9
=×3.14×32×9
=×3.14×9×9
=84.78(dm3)
圆锥体的体积是84.78dm3。
6.1392.5cm3
【分析】观察图形可知,立体图形的体积=棱长是10cm的正方体的体积+半径是(10÷2)cm,高是10cm的圆柱的体积的一半,根据正方体的体积公式:体积=棱长×棱长×棱长,圆柱的体积公式:体积=π×半径2×高,代入数据,即可解答。
【详解】10×10×10+3.14×(10÷2)2×10÷2
=10×10×10+3.14×52×10÷2
=100×10+3.14×25×10÷2
=1000+78.5×10÷2
=1000+785÷2
=1000+392.5
=1392.5(cm3)
立体图形的体积是1392.5cm3。
7.157立方厘米;635.5立方厘米
【分析】图一:用大圆柱的体积减去中间部分小圆柱的体积,根据圆柱的体积V=πr2h,代入数据解答即可;
图二:用圆锥的体积加上长方体的体积,根据圆锥的体积V=πr2h,长方体的体积V=abh,代入数据解答即可。
【详解】1+4+1=6(厘米)
3.14×(6÷2)2×10-3.14×(4÷2)2×10
=3.14×32×10-3.14×22×10
=3.14×9×10-3.14×4×10
=28.26×10-12.56×10
=282.6-125.6
=157(立方厘米)
3.14×(10÷2)2×9×+10×8×5
=3.14×52×9×+80×5
=3.14×25×9×+400
=78.5×9×+400
=706.5×+400
=235.5+400
=635.5(立方厘米)
图一的体积是157立方厘米,图二的体积是635.5立方厘米。
8.314cm3;113.04cm3
【分析】(1)图形是一个底面直径为10cm、高为12cm的圆锥,根据圆锥的体积公式V=πr2h,代入数据计算求解。
(2)图形是一个底面直径为6cm、高为8cm的半圆柱,根据圆柱的体积公式V=πr2h,求出圆柱的体积,再除以2即可。
【详解】(1)×3.14×(10÷2)2×12
=×3.14×52×12
=×3.14×25×12
=314(cm3)
圆锥的体积是314cm3。
(2)3.14×(6÷2)2×8÷2
=3.14×32×8÷2
=3.14×9×8÷2
=113.04(cm3)
圆柱的体积是113.04cm3。
9.125.6
【分析】2个完全一样的原图立体图形可以拼成一个高为(12+8)、底面直径是4的圆柱体,所以此图的体积是拼成的圆柱体积的一半;利用圆柱体的体积公式计算出体积即可。
【详解】
它的体积是125.6。
10.214.2立方厘米
【分析】观察图形可知,图形的体积=圆柱的体积×+长方体的体积,根据圆柱的体积公式V=πr2h,长方体的体积公式V=abh,代入数据计算即可求解。
【详解】3.14×22×10×+6×10×2
=3.14×4×10×+60×2
=94.2+120
=214.2(立方厘米)
图形的体积是214.2立方厘米。
11.66180立方厘米
【分析】由图可知,该图形的体积可由一个长70厘米,宽30厘米,高36厘米的长方体体积减去一个底面直径为20厘米,高为30厘米的圆柱体体积。根据及圆柱的体积公式代入数据解答。
【详解】
(立方厘米)
(立方厘米)
(立方厘米)
12.415.4平方厘米
【分析】通过观察图形可得:这个组合图形的表面积等于一个正方体的表面积加上一个圆柱的侧面积,根据正方体的表面积=棱长×棱长×6、圆柱的侧面积=底面周长×高,代入数据计算,即可解答。
【详解】表面积:
8×8×6+2×3.14×5
=384+31.4
=415.4(平方厘米)
13.168.84
【分析】观察图形可知,图形的表面积等于正方体表面积与圆柱侧面积之和,再根据正方体的表面积=棱长×棱长×6,圆柱侧面积=底面周长×高,进行解答即可。
【详解】正方体表面积:
(cm2)
圆柱侧面积:
(cm2)
几何体表面积:
14.2572立方厘米
【分析】求这个几何体的体积,用长方体的体积-圆柱的体积,长方体的体积=长×宽×高,圆柱的体积=底面积×高,据此列式解答。
【详解】10÷2=5(厘米)
20×20×8-3.14××8
=400×8-3.14×200
=3200-628
=2572(立方厘米)
15.87.92立方厘米
【分析】观察图形可知,图形的体积=圆柱的体积+圆锥的体积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算求解。
【详解】3.14×(4÷2)2×5+×3.14×(4÷2)2×6
=3.14×22×5+×3.14×22×6
=3.14×4×5+×3.14×4×6
=62.8+25.12
=87.92(立方厘米)
图形的体积是87.92立方厘米。
16.452.16
【分析】由图可知,此组合图形是由一个底面直径是6cm、高为12cm的圆柱体和一个底面直径是6cm、高为12cm的圆锥组合而成的。其组合图形的体积=圆柱体积+圆锥体积。根据圆柱体积公式V=πh和圆锥体积公式V=πh,代入数据求解即可。
【详解】3.14×(6÷2)2×12+3.14×(6÷2)2×12×
=3.14×32×12+3.14×32××4
=3.14×9×12+3.14×36
=339.12+113.04
=452.16()
所以,此组合体的体积是452.16。
17.142.84平方厘米
【分析】观察图形可知,组合体的表面积等于长方体的表面积加上圆柱体的侧面积,根据长方体的表面积公式:,圆柱体的侧面积公式:,代入数据计算即可。
【详解】
(平方厘米)
即组合体的表面积是142.84平方厘米。
18.dm3;m3
【分析】第一个图形是圆锥,根据圆锥的体积公式,其中直径是10分米,半径是直径的一半为5分米,高是12分米。第二个图形是圆柱,利用,其中半径是3米,高是7米。
【详解】
(dm3)
(m3)
19.471平方厘米
【分析】根据圆柱的表面积公式:S表=S侧+2S底=Ch+2πr2可知,需要先根据底面周长计算出底面半径,再求出底面积,进而求出圆柱的表面积。据此解答。
【详解】31.4÷3.14÷2
=10÷2
=5(厘米)
31.4×10+2×3.14×52
=314+157
=471(平方厘米)
圆柱的表面积是471平方厘米。
20.536.94 cm
【分析】根据图示,图形的体积等于两个圆锥的体积加圆柱的体积,圆锥的体积=×底面积×高,圆柱的体积=底面积×高,圆锥和圆柱的底面半径为(6÷2),圆锥的高为6,圆柱的高为15,代入数据计算即可。
【详解】×3.14×(6÷2)2×6×2+3.14×(6÷2)2×15
=3.14×36+3.14×135
=113.04+423.9
=536.94(cm )
21.7822.5立方厘米;6358.5立方厘米
【分析】观察第一个图形,是从一个长方体中截取了一个半圆柱,图形的体积=长方体的体积-半圆柱的体积,根据“V长方体=abh”“V圆柱=πr2h”,代入数据即可解答;
观察第二个图形可知:剩余部分的体积是圆柱与圆锥的体积之差,根据圆柱的体积:V=Sh,圆锥的体积公式:V=Sh,把数据分别代入公式解答即可。
【详解】第一个图形的体积:
30×20×15-3.14×(10÷2)2×30÷2
=30×20×15-3.14×25×30÷2
=600×15-78.5×30÷2
=9000-2355÷2
=9000-1177.5
=7822.5(立方厘米)
它的体积是7822.5立方厘米。
第二个图形的体积:
3.14×()2×30-×3.14×()2×15
=3.14×92×30-×3.14×92×15
=3.14×81×30-×3.14×81×15
=3.14×81×30-3.14×81×5
=254.34×30-254.34×5
=7630.2-1271.7
=6358.5(立方厘米)
它的体积是6358.5立方厘米。
22.2543.4立方米
【分析】圆柱体积=底面积×高,据此先分别求出大圆柱和小圆柱的体积,再相减即可得出题中图形的体积。
【详解】3.14×(10÷2)2×90-3.14×(8÷2)2×90
=3.14×52×90-3.14×42×90
=7065-4521.6
=2543.4(立方米)
所以,这个图形的体积是2543.4立方米。
23.675.36
【详解】由于正方体里面挖出一个圆柱,正方体的上面减少了一个圆柱的底面的面积,多了一个圆柱,会增加一个圆柱的底面积以及一个圆柱的侧面积,所以组合体的表面积=正方体的表方面积+圆柱的侧面积。利用正方体表面积=棱长×棱长×6,圆柱的侧面积=计算后再相加。据此解答。
【点睛】
=
=
图形的表面积是675.36。
24.62.8平方厘米
【分析】如图所示,整个图形的表面积=小圆柱体的侧面积+大圆柱体的表面积(注意扣除下底面的面积),据此解答。
【详解】小圆柱体的侧面积:
(平方厘米)
大圆柱体的表面积:
(平方厘米)
整个图形的表面积:(平方厘米)
中小学教育资源及组卷应用平台
2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算专题训练
1.第一个图(单位:cm)求表面积,第二个图求体积。
2.下面是圆柱的平面展开图,计算它的体积。(单位:厘米)
3.求下图立体图形的表面积。(单位:厘米)
4.求下图圆柱体的表面积。
5.求下图圆锥体的体积。
6.求下面立体图形的体积。
7.求下面立体图形的体积。(单位:厘米)
8.计算下面各图形的体积。(单位:cm)
9.求如图的体积。(π取3.14)
10.求图形的体积(单位:厘米)(π取3.14)。
11.求下面图形的体积。(单位:厘米)
12.计算如图形的表面积。(单位:厘米)
13.求下图所示几何体的表面积(单位:)。
14.从一个长方体上、下面上挖通一个圆柱形孔后得到下面几何体,求这个几何体的体积(单位:cm)。(取3.14)
15.求下面图形的体积。(单位:厘米,π取值为3.14)
16.求体积。
17.如图下图,求组合体的表面积。(单位:厘米;π取3.14)
18.计算下面各图形的体积。
19.求下面圆柱的表面积。
20.求如图所示图形的体积。(单位:cm)
21.求下面图形的体积。(左图中的半圆柱的底面直径是10厘米,右图是从圆柱中挖法一个圆锥后的剩余部分)。(单位:厘米)
22.计算下面图形的体积。(单位:米)
23.求下面图形的表面积。
24.求下面图形的表面积。(单位:厘米)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算专题训练》参考答案
1.(1)785cm2;(2)15.7cm3
【分析】(1)根据圆柱的表面积S表=S侧+2S底,其中S侧=πdh,S底=πr2,代入数据计算,即可求出圆柱的表面积。
(2)组合体的体积=圆柱的体积+圆锥的体积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算求解。
【详解】(1)3.14×10×20+3.14×(10÷2)2×2
=3.14×10×20+3.14×52×2
=628+3.14×25×2
=628+157
=785(cm2)
圆柱的表面积是785cm2。
(2)3.14×(2÷2)2×4+×3.14×(2÷2)2×3
=3.14×12×4+×3.14×12×3
=3.14×1×4+×3.14×1×3
=12.56+3.14
=15.7(cm3)
组合体的体积是15.7cm3。
2.141.3立方厘米
【分析】从圆柱的展开图中可知,圆柱的底面周长是18.84厘米,高是5厘米;先根据圆的周长公式C=2πr,可知r=C÷π÷2,由此求出圆柱的底面半径;再根据圆柱的体积公式V=πr2h,求出圆柱的体积。
【详解】底面半径:
18.84÷3.14÷2
=6÷2
=3(厘米)
体积:
3.14×32×5
=3.14×9×5
=141.3(立方厘米)
它的体积是141.3立方厘米。
3.228.8平方厘米
【分析】观察图形可知,圆柱和长方体有重合的部分,把圆柱的上底面向下平移,补给长方体的上面;这样长方体的表面积是6个面的面积之和,而圆柱只需计算侧面积即可;
图形的表面积=圆柱的侧面积+长方体的表面积
其中,圆柱的侧面积S侧=πdh,长方体的表面积S=2(ab+ah+bh),代入数据计算求解。
【详解】圆柱的侧面积:
3.14×4×5=62.8(平方厘米)
长方体的表面积:
(7×4+7×5+4×5)×2
=(28+35+20)×2
=83×2
=166(平方厘米)
组合体的表面积:
62.8+166=228.8(平方厘米)
图形的表面积是228.8平方厘米。
4.62.8cm2
【分析】从图中可知,圆柱的底面半径是2cm,高是3cm,根据圆柱的表面积公式S表=S侧+2S底,其中S侧=2πrh,S底=πr2,代入数据计算,即可求出这个圆柱的表面积。
【详解】2×3.14×2×3+3.14×22×2
=2×3.14×2×3+3.14×4×2
=37.68+25.12
=62.8(cm2)
圆柱体的表面积是62.8cm2。
5.84.78dm3
【分析】已知圆锥的底面直径是6dm,高是9dm,根据圆锥的体积公式V=πr2h,代入数据计算求出圆锥的体积。
【详解】×3.14×(6÷2)2×9
=×3.14×32×9
=×3.14×9×9
=84.78(dm3)
圆锥体的体积是84.78dm3。
6.1392.5cm3
【分析】观察图形可知,立体图形的体积=棱长是10cm的正方体的体积+半径是(10÷2)cm,高是10cm的圆柱的体积的一半,根据正方体的体积公式:体积=棱长×棱长×棱长,圆柱的体积公式:体积=π×半径2×高,代入数据,即可解答。
【详解】10×10×10+3.14×(10÷2)2×10÷2
=10×10×10+3.14×52×10÷2
=100×10+3.14×25×10÷2
=1000+78.5×10÷2
=1000+785÷2
=1000+392.5
=1392.5(cm3)
立体图形的体积是1392.5cm3。
7.157立方厘米;635.5立方厘米
【分析】图一:用大圆柱的体积减去中间部分小圆柱的体积,根据圆柱的体积V=πr2h,代入数据解答即可;
图二:用圆锥的体积加上长方体的体积,根据圆锥的体积V=πr2h,长方体的体积V=abh,代入数据解答即可。
【详解】1+4+1=6(厘米)
3.14×(6÷2)2×10-3.14×(4÷2)2×10
=3.14×32×10-3.14×22×10
=3.14×9×10-3.14×4×10
=28.26×10-12.56×10
=282.6-125.6
=157(立方厘米)
3.14×(10÷2)2×9×+10×8×5
=3.14×52×9×+80×5
=3.14×25×9×+400
=78.5×9×+400
=706.5×+400
=235.5+400
=635.5(立方厘米)
图一的体积是157立方厘米,图二的体积是635.5立方厘米。
8.314cm3;113.04cm3
【分析】(1)图形是一个底面直径为10cm、高为12cm的圆锥,根据圆锥的体积公式V=πr2h,代入数据计算求解。
(2)图形是一个底面直径为6cm、高为8cm的半圆柱,根据圆柱的体积公式V=πr2h,求出圆柱的体积,再除以2即可。
【详解】(1)×3.14×(10÷2)2×12
=×3.14×52×12
=×3.14×25×12
=314(cm3)
圆锥的体积是314cm3。
(2)3.14×(6÷2)2×8÷2
=3.14×32×8÷2
=3.14×9×8÷2
=113.04(cm3)
圆柱的体积是113.04cm3。
9.125.6
【分析】2个完全一样的原图立体图形可以拼成一个高为(12+8)、底面直径是4的圆柱体,所以此图的体积是拼成的圆柱体积的一半;利用圆柱体的体积公式计算出体积即可。
【详解】
它的体积是125.6。
10.214.2立方厘米
【分析】观察图形可知,图形的体积=圆柱的体积×+长方体的体积,根据圆柱的体积公式V=πr2h,长方体的体积公式V=abh,代入数据计算即可求解。
【详解】3.14×22×10×+6×10×2
=3.14×4×10×+60×2
=94.2+120
=214.2(立方厘米)
图形的体积是214.2立方厘米。
11.66180立方厘米
【分析】由图可知,该图形的体积可由一个长70厘米,宽30厘米,高36厘米的长方体体积减去一个底面直径为20厘米,高为30厘米的圆柱体体积。根据及圆柱的体积公式代入数据解答。
【详解】
(立方厘米)
(立方厘米)
(立方厘米)
12.415.4平方厘米
【分析】通过观察图形可得:这个组合图形的表面积等于一个正方体的表面积加上一个圆柱的侧面积,根据正方体的表面积=棱长×棱长×6、圆柱的侧面积=底面周长×高,代入数据计算,即可解答。
【详解】表面积:
8×8×6+2×3.14×5
=384+31.4
=415.4(平方厘米)
13.168.84
【分析】观察图形可知,图形的表面积等于正方体表面积与圆柱侧面积之和,再根据正方体的表面积=棱长×棱长×6,圆柱侧面积=底面周长×高,进行解答即可。
【详解】正方体表面积:
(cm2)
圆柱侧面积:
(cm2)
几何体表面积:
14.2572立方厘米
【分析】求这个几何体的体积,用长方体的体积-圆柱的体积,长方体的体积=长×宽×高,圆柱的体积=底面积×高,据此列式解答。
【详解】10÷2=5(厘米)
20×20×8-3.14××8
=400×8-3.14×200
=3200-628
=2572(立方厘米)
15.87.92立方厘米
【分析】观察图形可知,图形的体积=圆柱的体积+圆锥的体积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算求解。
【详解】3.14×(4÷2)2×5+×3.14×(4÷2)2×6
=3.14×22×5+×3.14×22×6
=3.14×4×5+×3.14×4×6
=62.8+25.12
=87.92(立方厘米)
图形的体积是87.92立方厘米。
16.452.16
【分析】由图可知,此组合图形是由一个底面直径是6cm、高为12cm的圆柱体和一个底面直径是6cm、高为12cm的圆锥组合而成的。其组合图形的体积=圆柱体积+圆锥体积。根据圆柱体积公式V=πh和圆锥体积公式V=πh,代入数据求解即可。
【详解】3.14×(6÷2)2×12+3.14×(6÷2)2×12×
=3.14×32×12+3.14×32××4
=3.14×9×12+3.14×36
=339.12+113.04
=452.16()
所以,此组合体的体积是452.16。
17.142.84平方厘米
【分析】观察图形可知,组合体的表面积等于长方体的表面积加上圆柱体的侧面积,根据长方体的表面积公式:,圆柱体的侧面积公式:,代入数据计算即可。
【详解】
(平方厘米)
即组合体的表面积是142.84平方厘米。
18.dm3;m3
【分析】第一个图形是圆锥,根据圆锥的体积公式,其中直径是10分米,半径是直径的一半为5分米,高是12分米。第二个图形是圆柱,利用,其中半径是3米,高是7米。
【详解】
(dm3)
(m3)
19.471平方厘米
【分析】根据圆柱的表面积公式:S表=S侧+2S底=Ch+2πr2可知,需要先根据底面周长计算出底面半径,再求出底面积,进而求出圆柱的表面积。据此解答。
【详解】31.4÷3.14÷2
=10÷2
=5(厘米)
31.4×10+2×3.14×52
=314+157
=471(平方厘米)
圆柱的表面积是471平方厘米。
20.536.94 cm
【分析】根据图示,图形的体积等于两个圆锥的体积加圆柱的体积,圆锥的体积=×底面积×高,圆柱的体积=底面积×高,圆锥和圆柱的底面半径为(6÷2),圆锥的高为6,圆柱的高为15,代入数据计算即可。
【详解】×3.14×(6÷2)2×6×2+3.14×(6÷2)2×15
=3.14×36+3.14×135
=113.04+423.9
=536.94(cm )
21.7822.5立方厘米;6358.5立方厘米
【分析】观察第一个图形,是从一个长方体中截取了一个半圆柱,图形的体积=长方体的体积-半圆柱的体积,根据“V长方体=abh”“V圆柱=πr2h”,代入数据即可解答;
观察第二个图形可知:剩余部分的体积是圆柱与圆锥的体积之差,根据圆柱的体积:V=Sh,圆锥的体积公式:V=Sh,把数据分别代入公式解答即可。
【详解】第一个图形的体积:
30×20×15-3.14×(10÷2)2×30÷2
=30×20×15-3.14×25×30÷2
=600×15-78.5×30÷2
=9000-2355÷2
=9000-1177.5
=7822.5(立方厘米)
它的体积是7822.5立方厘米。
第二个图形的体积:
3.14×()2×30-×3.14×()2×15
=3.14×92×30-×3.14×92×15
=3.14×81×30-×3.14×81×15
=3.14×81×30-3.14×81×5
=254.34×30-254.34×5
=7630.2-1271.7
=6358.5(立方厘米)
它的体积是6358.5立方厘米。
22.2543.4立方米
【分析】圆柱体积=底面积×高,据此先分别求出大圆柱和小圆柱的体积,再相减即可得出题中图形的体积。
【详解】3.14×(10÷2)2×90-3.14×(8÷2)2×90
=3.14×52×90-3.14×42×90
=7065-4521.6
=2543.4(立方米)
所以,这个图形的体积是2543.4立方米。
23.675.36
【详解】由于正方体里面挖出一个圆柱,正方体的上面减少了一个圆柱的底面的面积,多了一个圆柱,会增加一个圆柱的底面积以及一个圆柱的侧面积,所以组合体的表面积=正方体的表方面积+圆柱的侧面积。利用正方体表面积=棱长×棱长×6,圆柱的侧面积=计算后再相加。据此解答。
【点睛】
=
=
图形的表面积是675.36。
24.62.8平方厘米
【分析】如图所示,整个图形的表面积=小圆柱体的侧面积+大圆柱体的表面积(注意扣除下底面的面积),据此解答。
【详解】小圆柱体的侧面积:
(平方厘米)
大圆柱体的表面积:
(平方厘米)
整个图形的表面积:(平方厘米)
