华师大版七下(2024版)6.2.2二元一次方程组的解法—加减法——PPT
文档属性
| 名称 | 华师大版七下(2024版)6.2.2二元一次方程组的解法—加减法——PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 11:10:09 | ||
图片预览








文档简介
(共28张PPT)
第六章 一次方程组
6.2.2解二元一次方程组—加减法
01
教学目标
02
新知导入
03
新知讲解
04
新知巩固
05
课堂练习
06
课后作业
01
教学目标
掌握加减消元法的基本原理和步骤,能够灵活运用加减消元法解决不同类型的二元一次方程组。
01
通过观察、分析和讨论,培养学生发现问题、解决问题的能力和逻辑思维能力。
02
02
新知导入
例 3 解方程组:
探索 :注意到这个方程组的未知数相同 (都是 3 ). 把这两个方程的左、右两边分别相减, 能得到什么结果
02
新知导入
这两个方程的左、右两边分别相减,就消去了 ,得到
即
把 代入①,得
解得
这样,我们求得了一对 的值. 显然, 是原方程组的解.
03
新知讲解
思考 :从上面的解答过程中, 你发现了二元一次方程组的新解法吗
当二元一次方程组中同一未知数的系数相等或互为相反数时。
若系数相等,可通过两方程相减消去这个未知数;若系数互为相反数,可通过两方程相加消去这个未知数。
得到一个一元一次方程后,解这个一元一次方程求出一个未知数的值。
把求出的未知数的值代入原方程组中的任意一个方程,求出另一个未知数的值
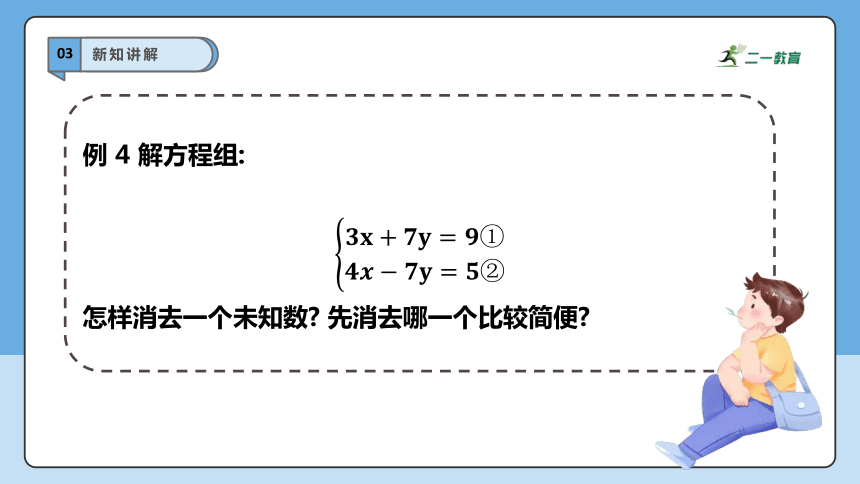
例 4 解方程组:
怎样消去一个未知数 先消去哪一个比较简便
03
新知讲解
解: ① + ②,得
即
将 代入①,得
解得
所以
03
新知讲解
【概括】在解例 3 、例 4 时, 我们是通过将两个方程的两边分别相加 (或相减) 消去一个未知数, 将方程组转化为一元一次方程来解的. 这种解法叫做加减消元法, 简称加减法.
“代入” 也好, “加减” 也罢,基本思想是通过 “消元”和“转化”, 将新问题“化归” 为老问题来解决.
03
新知讲解
1.用加减法解下列方程组 较简便的消元方法是:将两个方程_______,消去未知数_______.
2.已知方程组 ,用加减法消x的方法是:
用加减法消y的方法是:
给方程2x 3y=4两边同乘以3,给方程3x+2y=1两边同乘以2,然后把所得的两个方程相减
相加
y
给方程2x 3y=4两边同乘以2,给方程3x+2y=1两边同乘以3,然后把所得的两个方程相加。
03
拓展提升
在问题1中, 两个未知量 (比赛场数) 要满足两个等量关系. 相应地, 两个未知数 x" 、 " y 必须同时满足①②两个方程. 因此,把这两个方程合在一起,并写成
像这样, 两个二元一次方程合在一起, 就组成了一个二元一次方程组 ( system of linear equations with two unknowns).
03
新知讲解
例 5 解方程组:
直接相加减不能消去一个未知数, 怎么办呢
思考 :
例 3 和例 4 的方程组有一个共同特点, 即两个方程中有一个未知数的系数的绝对值相等, 所以可以直接通过加(或减) 消元. 这个方程组能不能通过变形, 转化成例 3 或例 4 的形式呢
03
新知讲解
解 ① ,② ,得
③ + ④,得
即
把 代入②,得
解得
所以
03
新知讲解
想一想,能否先消去 再求解 怎么做
请同学们回答:
03
新知讲解
解: ① ,② ,得
③ + ④,得
即
把 代入②,得
解得所以
03
新知讲解
试一试:在解本节例 2 的方程组
时, 用了什么方法 现在你不妨用加减法试一试, 看哪种方法比较简便.
03
新知讲解
用加减法解:方程组可化为
① ,② ,得
④-⑤,得
即
把 代入①,得
解得
所以
03
新知讲解
代入消元法需要先由一个方程用含一个未知数的式子表示另一个未知数,再代入另一个方程,在这个过程中可能会出现分数运算;而加减法通过将两个方程变形使某个未知数的系数相等或互为相反数,然后直接相减或相加消去这个未知数,避免了分数运算的复杂性。
因此,用加减法比较简便
03
新知讲解
04
课堂练习
1.解方程组 用加减法消去y,需要 ( )
A.①×2-② B.①×3-②×2
C.①×2+② D.①×3+②×2
2.用加减法解下列方程时,你认为先消哪个未知数较简单,填写消元的过程.
(1) 消元方法 __________________________.
(2) 消元方法 ____________________________.
c
方程①乘以2,然后减去方程②
方程②乘以3,然后加上方程①乘以2
04
课堂练习
3.用加减法解方程组:
解:
方程①乘以2:2(3x+y)=2 15 6x+2y=30
然后将这个结果与方程②相加:6x+2y+5x 2y=30+14 11x=44 x=4
将 x=4 代入方程①:3(4)+y=15 12+y=15 y=3
所以,方程组的解为 x=4,y=3
04
课堂练习
【选做题】
4.解方程组 的最佳方法是 ( )
A. 代入法消去a,由②得a=b+2
B. 代入法消去b,由①得b=7-2a
C. 加减法消去a,①-②×2得3b=3
D. 加减法消去b,①+②得3a=9
D
04
课堂练习
【选做题】
5.
解:①×6得:2(x+y)+3(x y)=36即 5x y=36
得到:
③×5得:5x 5y=180⑤
⑤+④得:x=8
将 x=8 代入方程②:y=4
所以,方程组的解为 x=8,y=4
04
课堂练习
6.已知 是二元一次方程组 的解,求m-n的值.
解:将 x= 1 和 y=2 代入第一个方程:3( 1)+2(2)=m 3+4=m m=1
将 x= 1 和 y=2 代入第二个方程:n( 1) 2=1 n 2=1 n=3 n= 3
所以,m n=1 ( 3)=1+3=4。
05
课堂总结
通过将两个方程的两边分别相加 (或相减) 消去一个未知数, 将方程组转化为一元一次方程来解的. 这种解法叫做加减消元法, 简称加减法.
“代入” 也好, “加减” 也罢,基本思想是通过 “消元”和“转化”, 将新问题“化归” 为老问题来解决.
06
课后作业
【知识技能类作业】必做题:
1.已知a,b 满足方程组 则a+b的值为 ( )
A.1 B. -1 C. -3 D.3
2.若 方 程 组 月 的解相同,则a+b= .
3.若实数a 与b 满足(4a- 则 ab的平方根为
D
5
±2
【综合拓展类作业】选做题
4.已知关于x,y的方程组 与 的解相同,
求 mn的值.
06
课后作业
06
课后作业
解:从第一个方程组中,2x+y=3 和 3x 2y=1 可以解出 x 和 y:解得 x=1 和 y=1。
将 x=1 和 y=1 代入第二个方程组:
ax+by=12 a(1)+b(1)=12 a+b=12
bx+ay=13 b(1)+a(1)=13 b+a=13
从第二个方程组中,3x 2y=1 和 nx y=2 可以解出 n:
3(1) 2(1)=1 3 2=1(验证)
n(1) 1=2 n 1=2 n=3
从第一个方程组中,2x+y=3 和 x my=4 可以解出 m:
2(1)+1=3(验证)
1 m(1)=4 1 m=4 m= 3
所以,mn=3 ( 3)= 9。 答案是:-9
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第六章 一次方程组
6.2.2解二元一次方程组—加减法
01
教学目标
02
新知导入
03
新知讲解
04
新知巩固
05
课堂练习
06
课后作业
01
教学目标
掌握加减消元法的基本原理和步骤,能够灵活运用加减消元法解决不同类型的二元一次方程组。
01
通过观察、分析和讨论,培养学生发现问题、解决问题的能力和逻辑思维能力。
02
02
新知导入
例 3 解方程组:
探索 :注意到这个方程组的未知数相同 (都是 3 ). 把这两个方程的左、右两边分别相减, 能得到什么结果
02
新知导入
这两个方程的左、右两边分别相减,就消去了 ,得到
即
把 代入①,得
解得
这样,我们求得了一对 的值. 显然, 是原方程组的解.
03
新知讲解
思考 :从上面的解答过程中, 你发现了二元一次方程组的新解法吗
当二元一次方程组中同一未知数的系数相等或互为相反数时。
若系数相等,可通过两方程相减消去这个未知数;若系数互为相反数,可通过两方程相加消去这个未知数。
得到一个一元一次方程后,解这个一元一次方程求出一个未知数的值。
把求出的未知数的值代入原方程组中的任意一个方程,求出另一个未知数的值
例 4 解方程组:
怎样消去一个未知数 先消去哪一个比较简便
03
新知讲解
解: ① + ②,得
即
将 代入①,得
解得
所以
03
新知讲解
【概括】在解例 3 、例 4 时, 我们是通过将两个方程的两边分别相加 (或相减) 消去一个未知数, 将方程组转化为一元一次方程来解的. 这种解法叫做加减消元法, 简称加减法.
“代入” 也好, “加减” 也罢,基本思想是通过 “消元”和“转化”, 将新问题“化归” 为老问题来解决.
03
新知讲解
1.用加减法解下列方程组 较简便的消元方法是:将两个方程_______,消去未知数_______.
2.已知方程组 ,用加减法消x的方法是:
用加减法消y的方法是:
给方程2x 3y=4两边同乘以3,给方程3x+2y=1两边同乘以2,然后把所得的两个方程相减
相加
y
给方程2x 3y=4两边同乘以2,给方程3x+2y=1两边同乘以3,然后把所得的两个方程相加。
03
拓展提升
在问题1中, 两个未知量 (比赛场数) 要满足两个等量关系. 相应地, 两个未知数 x" 、 " y 必须同时满足①②两个方程. 因此,把这两个方程合在一起,并写成
像这样, 两个二元一次方程合在一起, 就组成了一个二元一次方程组 ( system of linear equations with two unknowns).
03
新知讲解
例 5 解方程组:
直接相加减不能消去一个未知数, 怎么办呢
思考 :
例 3 和例 4 的方程组有一个共同特点, 即两个方程中有一个未知数的系数的绝对值相等, 所以可以直接通过加(或减) 消元. 这个方程组能不能通过变形, 转化成例 3 或例 4 的形式呢
03
新知讲解
解 ① ,② ,得
③ + ④,得
即
把 代入②,得
解得
所以
03
新知讲解
想一想,能否先消去 再求解 怎么做
请同学们回答:
03
新知讲解
解: ① ,② ,得
③ + ④,得
即
把 代入②,得
解得所以
03
新知讲解
试一试:在解本节例 2 的方程组
时, 用了什么方法 现在你不妨用加减法试一试, 看哪种方法比较简便.
03
新知讲解
用加减法解:方程组可化为
① ,② ,得
④-⑤,得
即
把 代入①,得
解得
所以
03
新知讲解
代入消元法需要先由一个方程用含一个未知数的式子表示另一个未知数,再代入另一个方程,在这个过程中可能会出现分数运算;而加减法通过将两个方程变形使某个未知数的系数相等或互为相反数,然后直接相减或相加消去这个未知数,避免了分数运算的复杂性。
因此,用加减法比较简便
03
新知讲解
04
课堂练习
1.解方程组 用加减法消去y,需要 ( )
A.①×2-② B.①×3-②×2
C.①×2+② D.①×3+②×2
2.用加减法解下列方程时,你认为先消哪个未知数较简单,填写消元的过程.
(1) 消元方法 __________________________.
(2) 消元方法 ____________________________.
c
方程①乘以2,然后减去方程②
方程②乘以3,然后加上方程①乘以2
04
课堂练习
3.用加减法解方程组:
解:
方程①乘以2:2(3x+y)=2 15 6x+2y=30
然后将这个结果与方程②相加:6x+2y+5x 2y=30+14 11x=44 x=4
将 x=4 代入方程①:3(4)+y=15 12+y=15 y=3
所以,方程组的解为 x=4,y=3
04
课堂练习
【选做题】
4.解方程组 的最佳方法是 ( )
A. 代入法消去a,由②得a=b+2
B. 代入法消去b,由①得b=7-2a
C. 加减法消去a,①-②×2得3b=3
D. 加减法消去b,①+②得3a=9
D
04
课堂练习
【选做题】
5.
解:①×6得:2(x+y)+3(x y)=36即 5x y=36
得到:
③×5得:5x 5y=180⑤
⑤+④得:x=8
将 x=8 代入方程②:y=4
所以,方程组的解为 x=8,y=4
04
课堂练习
6.已知 是二元一次方程组 的解,求m-n的值.
解:将 x= 1 和 y=2 代入第一个方程:3( 1)+2(2)=m 3+4=m m=1
将 x= 1 和 y=2 代入第二个方程:n( 1) 2=1 n 2=1 n=3 n= 3
所以,m n=1 ( 3)=1+3=4。
05
课堂总结
通过将两个方程的两边分别相加 (或相减) 消去一个未知数, 将方程组转化为一元一次方程来解的. 这种解法叫做加减消元法, 简称加减法.
“代入” 也好, “加减” 也罢,基本思想是通过 “消元”和“转化”, 将新问题“化归” 为老问题来解决.
06
课后作业
【知识技能类作业】必做题:
1.已知a,b 满足方程组 则a+b的值为 ( )
A.1 B. -1 C. -3 D.3
2.若 方 程 组 月 的解相同,则a+b= .
3.若实数a 与b 满足(4a- 则 ab的平方根为
D
5
±2
【综合拓展类作业】选做题
4.已知关于x,y的方程组 与 的解相同,
求 mn的值.
06
课后作业
06
课后作业
解:从第一个方程组中,2x+y=3 和 3x 2y=1 可以解出 x 和 y:解得 x=1 和 y=1。
将 x=1 和 y=1 代入第二个方程组:
ax+by=12 a(1)+b(1)=12 a+b=12
bx+ay=13 b(1)+a(1)=13 b+a=13
从第二个方程组中,3x 2y=1 和 nx y=2 可以解出 n:
3(1) 2(1)=1 3 2=1(验证)
n(1) 1=2 n 1=2 n=3
从第一个方程组中,2x+y=3 和 x my=4 可以解出 m:
2(1)+1=3(验证)
1 m(1)=4 1 m=4 m= 3
所以,mn=3 ( 3)= 9。 答案是:-9
Thanks!
https://www.21cnjy.com/recruitment/home/fine
