华东师大版2024—2025学年八年级下学期数学第一次月考模拟试卷A卷(含解析)
文档属性
| 名称 | 华东师大版2024—2025学年八年级下学期数学第一次月考模拟试卷A卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 342.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 16:12:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
华东师大版2024—2025学年八年级下学期数学第一次月考模拟试卷A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
考试范围:第十六章和第十七章
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.把0.00000000120用科学记数法表示为( )
A.1.2×10﹣9 B.1.20×10﹣9 C.1.2×10﹣8 D.1.2×10﹣10
2.下列变形从左到右正确的是( )
A. B.
C. D.
3.已知x﹣3y=0,且y≠0,则(1) 的值等于( )
A.2 B. C. D.3
4.某人生产一种零件,计划在30天内完成,若每天多生产6个,则25天完成且还多生产10个,问原计划每天生产多少个零件?设原计划每天生产x个,列方程式是( )
A. B. C. D.
5.如果把分式中的x和y都扩大3倍,那么分式的值( )
A.扩大3倍 B.缩小3倍 C.不变 D.扩大9倍
6.若分式的值为0,则a满足( )
A.a=3 B.a=﹣3 C.a=±3 D.a=3或a=﹣2
7.若关于x的分式方程2有增根,则m的值为( )
A.2 B.﹣3 C.﹣1 D.3
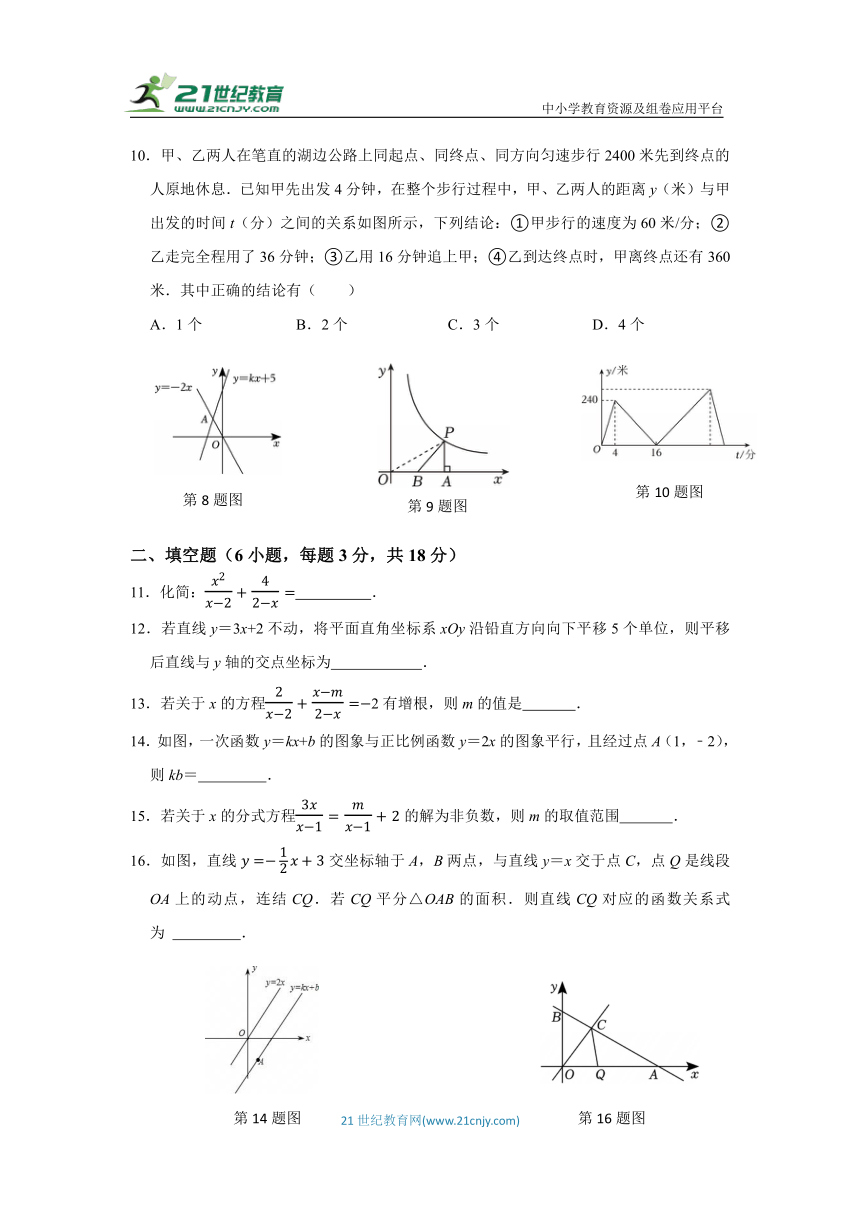
8.如图,函数y=﹣2x和y=kx+5的图象相交于点A(a,2),则不等式﹣2x≤kx+5的解集为( )
A.x≤2 B.x≥﹣1 C.x≤﹣1 D.x>﹣1
9.如图,在平面直角坐标系中,点P在反比例函数y(x>0)的图象上,过点P作PA⊥x轴于点A,点B是OA的中点,连结PB,则△PAB的面积为( )
A.6 B.12 C.3 D.4
10.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了36分钟;③乙用16分钟追上甲;④乙到达终点时,甲离终点还有360米.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(6小题,每题3分,共18分)
11.化简: .
12.若直线y=3x+2不动,将平面直角坐标系xOy沿铅直方向向下平移5个单位,则平移后直线与y轴的交点坐标为 .
13.若关于x的方程2有增根,则m的值是 .
14.如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行,且经过点A(1,﹣2),则kb= .
15.若关于x的分式方程的解为非负数,则m的取值范围 .
16.如图,直线交坐标轴于A,B两点,与直线y=x交于点C,点Q是线段OA上的动点,连结CQ.若CQ平分△OAB的面积.则直线CQ对应的函数关系式为 .
第II卷
华东师大版2024—2025学年八年级下学期数学第一次月考模拟试卷A卷
姓名:____________ 学号:____________准考证号:___________
题号 一 二 三 总分
17 18 19 20 21 22 23 24 25
得分
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程:
(1); (2).
18.先化简代数式,再选一个你喜欢的整数作为a的值代入求值.
19.计算:
(1); (2).
20.某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
21.若关于x的方程:.
(1)有增根,求a的值;
(2)无解,求a的值.
22.在平面直角坐标系中,一次函数yx+b的图象与y轴交于点B(0,2),与反比例函数y的图象交于点A(4,﹣1).
(1)求反比例函数的表达式和一次函数表达式;
(2)如果点P是x轴上的一点,且△ABP的面积是3,求P点的坐标.
23.已知动点P以每秒2cm的速度沿如图甲所示的边框按从B C D E F A的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙所示,若AB=6cm,试回答下列问题:
(1)动点P在线段 上运动的过程中△ABP的面积S保持不变.
(2)BC= cm;CD= cm;DE= cm;EF= cm.
(3)求出图乙中的a与b的值.
(4)在上述运动过程中,求出△ABP面积的最大值.
24.阅读下列材料:求分式方程的解,不妨设k=ab,m=a+b,可得x1=a,x2=b是该分式方程的解.例如:求分式方程的解,可发现k=6=(﹣2)×(﹣3),m=﹣5=(﹣2)+(﹣3),容易检验x1=﹣2,x2=﹣3是该方程的解.根据以上材料回答下列问题:
(1)求分式方程的解;
(2)若x1=m,x2=n是分式方程的两个解,求的值;
(3)设a为常数且a≠0,若关于x的分式方程的两个解分别为x1,x2,求的值.
25.在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B.若点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.
(1)k的值是 ;
(2)若点C在线段AB上,∠ECD=90°,是否存在点C,使CE=CD,若存在,求出点C的坐标,若不存在,说明理由.
(3)若已知点D的坐标为(6,0),点E的坐标为(0,1),且四边形OECD的面积是9,求点C的坐标.
(4)当CE平行于x轴,CD平行于y轴时,若四边形OECD的周长是10,请直接写出点C的坐标.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C B C B A B C B
二、填空题
11.【解答】解:
=x+2.
故答案为:x+2.
12.【解答】解:坐标系下移,得图象上移,得y=3x+2+5,即y=3x+7,
令x=0,则y=7,
则平移后直线与y轴的交点坐标为(0,7)
故答案为(0,7).
13.【解答】解:去分母得2﹣(x﹣m)=﹣2(x﹣2),
解得x=2﹣m,
当x=2时,原方程有增根,即2﹣m=2,解得m=0.
故答案为0.
14.【解答】解:∵y=kx+b的图象与正比例函数y=2x的图象平行,
∴k=2,
∵y=kx+b的图象经过点A(1,﹣2),
∴2+b=﹣2,
解得b=﹣4,
∴kb=2×(﹣4)=﹣8.
故答案为:﹣8.
15.【解答】解:方程两边同时乘以(x﹣1)得:
3x=m+2(x﹣1),
解得:x=m﹣2,
∵x为非负数,
∴m﹣2≥0,解得m≥2,
∵x≠1,
∴m﹣2≠1,即m≠3,
∴m的取值范围是m≥2且m≠3,
故答案为:m≥2且m≠3.
16.【解答】解:∵直线交坐标轴于A,B两点,
∴A(6,0),B(0,3),
∴OA=6,OB=3,
∴S△AOB9,
由,得,
∴C(2,2),
设Q(m,0),
∴AQ=6﹣m,
∵CQ平分△OAB的面积,
∴(6﹣m)×2,
∴m,
∴Q(,0),
设直线CQ的解析式是y=kx+b,
把C(2,2),Q(,0)代入得:,
解得:,
∴直线CQ对应的函数关系式为:y=4x﹣6.
故答案为:y=4x﹣6.
三、解答题
17.【解答】解:(1),
∴2x+1=3(x﹣1),
∴2x+1=3x﹣3,
解得:x=4,
经检验,x=4是原方程的解,
∴原方程的解为:x=4;
(2),
∴9x﹣3+3x=1,
解得:;
时,3x﹣1=0,
∴是原方程增根,
∴原方程无解.
18.【解答】解:
.
当a=0时,原式.
19.【解答】解:(1)原式;
(2)原式=2024+1﹣25=2000.
20.【解答】解:(1)设甲种树苗每棵的价格是x元,则乙种树苗每棵的价格是(x+10)元,依题意有
,
解得:x=30.
经检验,x=30是原方程的解,
x+10=30+10=40.
答:甲种树苗每棵的价格是30元,乙种树苗每棵的价格是40元.
(2)设他们可购买y棵乙种树苗,依题意有
30×(1﹣10%)(50﹣y)+40y≤1500,
解得y≤11,
∵y为整数,
∴y最大为11.
答:他们最多可购买11棵乙种树苗.
21.【解答】解:分式方程去分母得:3x+9+ax=4x﹣12,
(1)由分式方程有增根,得到(x+3)(x﹣3)=0,即x=3或x=﹣3,
把x=3代入整式方程得:18+3a=0,即a=﹣6;
把x=﹣3代入整式方程得:﹣3a=﹣24,即a=8,
综上,a的值为﹣6或8;
(2)整式方程整理得:(a﹣1)x=﹣21,
由方程无解,得到a﹣1=0,即a=1或8或﹣6.
22.【解答】解:(1)∵一次函数yx+b的图象与y轴交于点B(0,2),
∴b=2,
∴一次函数的关系式为yx+2;
∵反比例函数y的图象过点A(4,﹣1).
∴m=﹣4,
∴反比例函数的关系式为y;
(2)设直线yx+2与x轴的交点为M;则M(,0),
由△ABP的面积是3得,
PM×2PM×1=3,
∴PM=2,
当点P在点M的右侧,则OP=OM+PM2,因此点P(,0),
当点P在点M的左侧,则OP=OM﹣PM2,因此点P(,0),
∴点P的坐标为(,0)或(,0).
23.【解答】解:(1)如图甲所示,动点P在线段 CD和EF上运动的过程中△ABP的面积S保持不变.
故答案为:CD和EF;
(2)已知当P在BC上时,以AB为底的高在不断增大,到达点C时,开始不变,由第二个图得,
P在BC上移动了4秒,那么BC=4×2=8cm.
在CD上移动了2秒,CD=2×2=4cm,
在DE上移动了3秒,DE=3×2=6cm,而AB=6cm,
那么EF=AB﹣CD=2cm,
故答案为:8cm;4cm;6cm;2cm;
(3)由图得,a是点P运行4秒时△ABP的面积,
∴S△ABP6×8=24…8分
b为点P走完全程的时间为:t=9+1+7=17s
∴a=24 b=17;
(4)∵点P移动到点E时面积达到最大值a,
∴SAB (BC+DE),
∵AB=6cm,BC=8cm,DE=6cm,
∴S6×(8+6)=42(cm2).
24.【解答】解:(1)可化为x(﹣1)+(﹣5),
∴x1=﹣1,x2=﹣5.
经检验x1=﹣1,x2=﹣5是该方程的解.
(2)由已知得mn=﹣3,m+n=4,
∴
.
(3)原方程变为x+1a+(a+2),
∴x1+1=a,x2+1=a+2,
∴x1=a﹣1,x2=a+1,
∴x1﹣x2=a﹣1﹣(a+1)=﹣2,
∴(﹣2)2=4.
25.【解答】解:(1)将A(8,0)代入y=kx+4,得:0=8k+4,
解得:k,
故答案为:;
(2)存在,点C的坐标为(,).
如图,过点C作CM⊥x轴于M,过点C作CN⊥y轴于N,
∵∠AOB=∠CNO=∠CMO=90°,
∴∠MCN=90°,
∴∠NCE+∠ECM=90°,
∵∠ECD=90°,
∴∠MCD+∠ECM=90°,
∴∠NCE=∠MCD,
∵CE=CD,
∴△CMD≌△CNE(AAS),
∴CM=CN,
设C(x,x+4),则xx+4,
解得x,
∴C(,);
(3)如图,
由(1)可知直线AB的解析式为yx+4.
设C(m,m+4)(0<m<8),
∵点D的坐标为(6,0),点E的坐标为(0,1),
∴OD=6,OE=1,
∴OM=m,CMm+4,
∵四边形OECD的面积是9,
∴S梯形CEOM+S△CDM(1m+4) m(m+4) (6﹣m)=9,
整理得2m=6,
解得m=3,
∴点C的坐标为(3,);
(4)∵CE平行于x轴,CD平行于y轴,
∴四边形CEOD是矩形,
∵四边形OECD的周长是10,
设C(m,m+4),
∴2(mm+4)=10或2(m+4﹣m)=10,
解得m=2或m,
点C的坐标为(2,3)或(,).
21世纪教育网(www.21cnjy.com)
华东师大版2024—2025学年八年级下学期数学第一次月考模拟试卷A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
考试范围:第十六章和第十七章
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.把0.00000000120用科学记数法表示为( )
A.1.2×10﹣9 B.1.20×10﹣9 C.1.2×10﹣8 D.1.2×10﹣10
2.下列变形从左到右正确的是( )
A. B.
C. D.
3.已知x﹣3y=0,且y≠0,则(1) 的值等于( )
A.2 B. C. D.3
4.某人生产一种零件,计划在30天内完成,若每天多生产6个,则25天完成且还多生产10个,问原计划每天生产多少个零件?设原计划每天生产x个,列方程式是( )
A. B. C. D.
5.如果把分式中的x和y都扩大3倍,那么分式的值( )
A.扩大3倍 B.缩小3倍 C.不变 D.扩大9倍
6.若分式的值为0,则a满足( )
A.a=3 B.a=﹣3 C.a=±3 D.a=3或a=﹣2
7.若关于x的分式方程2有增根,则m的值为( )
A.2 B.﹣3 C.﹣1 D.3
8.如图,函数y=﹣2x和y=kx+5的图象相交于点A(a,2),则不等式﹣2x≤kx+5的解集为( )
A.x≤2 B.x≥﹣1 C.x≤﹣1 D.x>﹣1
9.如图,在平面直角坐标系中,点P在反比例函数y(x>0)的图象上,过点P作PA⊥x轴于点A,点B是OA的中点,连结PB,则△PAB的面积为( )
A.6 B.12 C.3 D.4
10.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了36分钟;③乙用16分钟追上甲;④乙到达终点时,甲离终点还有360米.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(6小题,每题3分,共18分)
11.化简: .
12.若直线y=3x+2不动,将平面直角坐标系xOy沿铅直方向向下平移5个单位,则平移后直线与y轴的交点坐标为 .
13.若关于x的方程2有增根,则m的值是 .
14.如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行,且经过点A(1,﹣2),则kb= .
15.若关于x的分式方程的解为非负数,则m的取值范围 .
16.如图,直线交坐标轴于A,B两点,与直线y=x交于点C,点Q是线段OA上的动点,连结CQ.若CQ平分△OAB的面积.则直线CQ对应的函数关系式为 .
第II卷
华东师大版2024—2025学年八年级下学期数学第一次月考模拟试卷A卷
姓名:____________ 学号:____________准考证号:___________
题号 一 二 三 总分
17 18 19 20 21 22 23 24 25
得分
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程:
(1); (2).
18.先化简代数式,再选一个你喜欢的整数作为a的值代入求值.
19.计算:
(1); (2).
20.某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
21.若关于x的方程:.
(1)有增根,求a的值;
(2)无解,求a的值.
22.在平面直角坐标系中,一次函数yx+b的图象与y轴交于点B(0,2),与反比例函数y的图象交于点A(4,﹣1).
(1)求反比例函数的表达式和一次函数表达式;
(2)如果点P是x轴上的一点,且△ABP的面积是3,求P点的坐标.
23.已知动点P以每秒2cm的速度沿如图甲所示的边框按从B C D E F A的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙所示,若AB=6cm,试回答下列问题:
(1)动点P在线段 上运动的过程中△ABP的面积S保持不变.
(2)BC= cm;CD= cm;DE= cm;EF= cm.
(3)求出图乙中的a与b的值.
(4)在上述运动过程中,求出△ABP面积的最大值.
24.阅读下列材料:求分式方程的解,不妨设k=ab,m=a+b,可得x1=a,x2=b是该分式方程的解.例如:求分式方程的解,可发现k=6=(﹣2)×(﹣3),m=﹣5=(﹣2)+(﹣3),容易检验x1=﹣2,x2=﹣3是该方程的解.根据以上材料回答下列问题:
(1)求分式方程的解;
(2)若x1=m,x2=n是分式方程的两个解,求的值;
(3)设a为常数且a≠0,若关于x的分式方程的两个解分别为x1,x2,求的值.
25.在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B.若点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.
(1)k的值是 ;
(2)若点C在线段AB上,∠ECD=90°,是否存在点C,使CE=CD,若存在,求出点C的坐标,若不存在,说明理由.
(3)若已知点D的坐标为(6,0),点E的坐标为(0,1),且四边形OECD的面积是9,求点C的坐标.
(4)当CE平行于x轴,CD平行于y轴时,若四边形OECD的周长是10,请直接写出点C的坐标.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C B C B A B C B
二、填空题
11.【解答】解:
=x+2.
故答案为:x+2.
12.【解答】解:坐标系下移,得图象上移,得y=3x+2+5,即y=3x+7,
令x=0,则y=7,
则平移后直线与y轴的交点坐标为(0,7)
故答案为(0,7).
13.【解答】解:去分母得2﹣(x﹣m)=﹣2(x﹣2),
解得x=2﹣m,
当x=2时,原方程有增根,即2﹣m=2,解得m=0.
故答案为0.
14.【解答】解:∵y=kx+b的图象与正比例函数y=2x的图象平行,
∴k=2,
∵y=kx+b的图象经过点A(1,﹣2),
∴2+b=﹣2,
解得b=﹣4,
∴kb=2×(﹣4)=﹣8.
故答案为:﹣8.
15.【解答】解:方程两边同时乘以(x﹣1)得:
3x=m+2(x﹣1),
解得:x=m﹣2,
∵x为非负数,
∴m﹣2≥0,解得m≥2,
∵x≠1,
∴m﹣2≠1,即m≠3,
∴m的取值范围是m≥2且m≠3,
故答案为:m≥2且m≠3.
16.【解答】解:∵直线交坐标轴于A,B两点,
∴A(6,0),B(0,3),
∴OA=6,OB=3,
∴S△AOB9,
由,得,
∴C(2,2),
设Q(m,0),
∴AQ=6﹣m,
∵CQ平分△OAB的面积,
∴(6﹣m)×2,
∴m,
∴Q(,0),
设直线CQ的解析式是y=kx+b,
把C(2,2),Q(,0)代入得:,
解得:,
∴直线CQ对应的函数关系式为:y=4x﹣6.
故答案为:y=4x﹣6.
三、解答题
17.【解答】解:(1),
∴2x+1=3(x﹣1),
∴2x+1=3x﹣3,
解得:x=4,
经检验,x=4是原方程的解,
∴原方程的解为:x=4;
(2),
∴9x﹣3+3x=1,
解得:;
时,3x﹣1=0,
∴是原方程增根,
∴原方程无解.
18.【解答】解:
.
当a=0时,原式.
19.【解答】解:(1)原式;
(2)原式=2024+1﹣25=2000.
20.【解答】解:(1)设甲种树苗每棵的价格是x元,则乙种树苗每棵的价格是(x+10)元,依题意有
,
解得:x=30.
经检验,x=30是原方程的解,
x+10=30+10=40.
答:甲种树苗每棵的价格是30元,乙种树苗每棵的价格是40元.
(2)设他们可购买y棵乙种树苗,依题意有
30×(1﹣10%)(50﹣y)+40y≤1500,
解得y≤11,
∵y为整数,
∴y最大为11.
答:他们最多可购买11棵乙种树苗.
21.【解答】解:分式方程去分母得:3x+9+ax=4x﹣12,
(1)由分式方程有增根,得到(x+3)(x﹣3)=0,即x=3或x=﹣3,
把x=3代入整式方程得:18+3a=0,即a=﹣6;
把x=﹣3代入整式方程得:﹣3a=﹣24,即a=8,
综上,a的值为﹣6或8;
(2)整式方程整理得:(a﹣1)x=﹣21,
由方程无解,得到a﹣1=0,即a=1或8或﹣6.
22.【解答】解:(1)∵一次函数yx+b的图象与y轴交于点B(0,2),
∴b=2,
∴一次函数的关系式为yx+2;
∵反比例函数y的图象过点A(4,﹣1).
∴m=﹣4,
∴反比例函数的关系式为y;
(2)设直线yx+2与x轴的交点为M;则M(,0),
由△ABP的面积是3得,
PM×2PM×1=3,
∴PM=2,
当点P在点M的右侧,则OP=OM+PM2,因此点P(,0),
当点P在点M的左侧,则OP=OM﹣PM2,因此点P(,0),
∴点P的坐标为(,0)或(,0).
23.【解答】解:(1)如图甲所示,动点P在线段 CD和EF上运动的过程中△ABP的面积S保持不变.
故答案为:CD和EF;
(2)已知当P在BC上时,以AB为底的高在不断增大,到达点C时,开始不变,由第二个图得,
P在BC上移动了4秒,那么BC=4×2=8cm.
在CD上移动了2秒,CD=2×2=4cm,
在DE上移动了3秒,DE=3×2=6cm,而AB=6cm,
那么EF=AB﹣CD=2cm,
故答案为:8cm;4cm;6cm;2cm;
(3)由图得,a是点P运行4秒时△ABP的面积,
∴S△ABP6×8=24…8分
b为点P走完全程的时间为:t=9+1+7=17s
∴a=24 b=17;
(4)∵点P移动到点E时面积达到最大值a,
∴SAB (BC+DE),
∵AB=6cm,BC=8cm,DE=6cm,
∴S6×(8+6)=42(cm2).
24.【解答】解:(1)可化为x(﹣1)+(﹣5),
∴x1=﹣1,x2=﹣5.
经检验x1=﹣1,x2=﹣5是该方程的解.
(2)由已知得mn=﹣3,m+n=4,
∴
.
(3)原方程变为x+1a+(a+2),
∴x1+1=a,x2+1=a+2,
∴x1=a﹣1,x2=a+1,
∴x1﹣x2=a﹣1﹣(a+1)=﹣2,
∴(﹣2)2=4.
25.【解答】解:(1)将A(8,0)代入y=kx+4,得:0=8k+4,
解得:k,
故答案为:;
(2)存在,点C的坐标为(,).
如图,过点C作CM⊥x轴于M,过点C作CN⊥y轴于N,
∵∠AOB=∠CNO=∠CMO=90°,
∴∠MCN=90°,
∴∠NCE+∠ECM=90°,
∵∠ECD=90°,
∴∠MCD+∠ECM=90°,
∴∠NCE=∠MCD,
∵CE=CD,
∴△CMD≌△CNE(AAS),
∴CM=CN,
设C(x,x+4),则xx+4,
解得x,
∴C(,);
(3)如图,
由(1)可知直线AB的解析式为yx+4.
设C(m,m+4)(0<m<8),
∵点D的坐标为(6,0),点E的坐标为(0,1),
∴OD=6,OE=1,
∴OM=m,CMm+4,
∵四边形OECD的面积是9,
∴S梯形CEOM+S△CDM(1m+4) m(m+4) (6﹣m)=9,
整理得2m=6,
解得m=3,
∴点C的坐标为(3,);
(4)∵CE平行于x轴,CD平行于y轴,
∴四边形CEOD是矩形,
∵四边形OECD的周长是10,
设C(m,m+4),
∴2(mm+4)=10或2(m+4﹣m)=10,
解得m=2或m,
点C的坐标为(2,3)或(,).
21世纪教育网(www.21cnjy.com)
同课章节目录
