全等三角形的基本题型(含答案）

全等三角形的基本题型
一．解答题（共29小题）
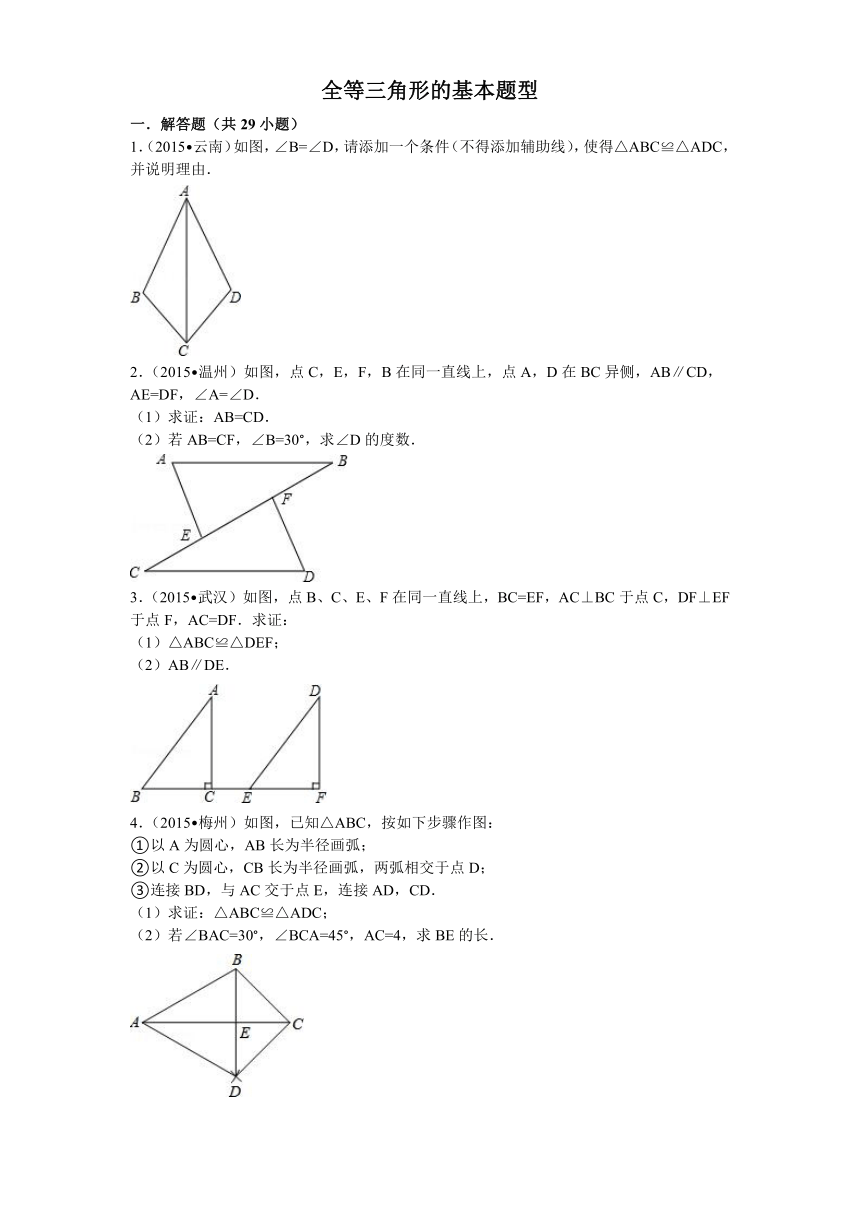
1．（2015 云南）如图，∠B=∠D，请添加一个条件（不得添加辅助线），使得△ABC≌△ADC，并说明理由．
( http: / / www.21cnjy.com )
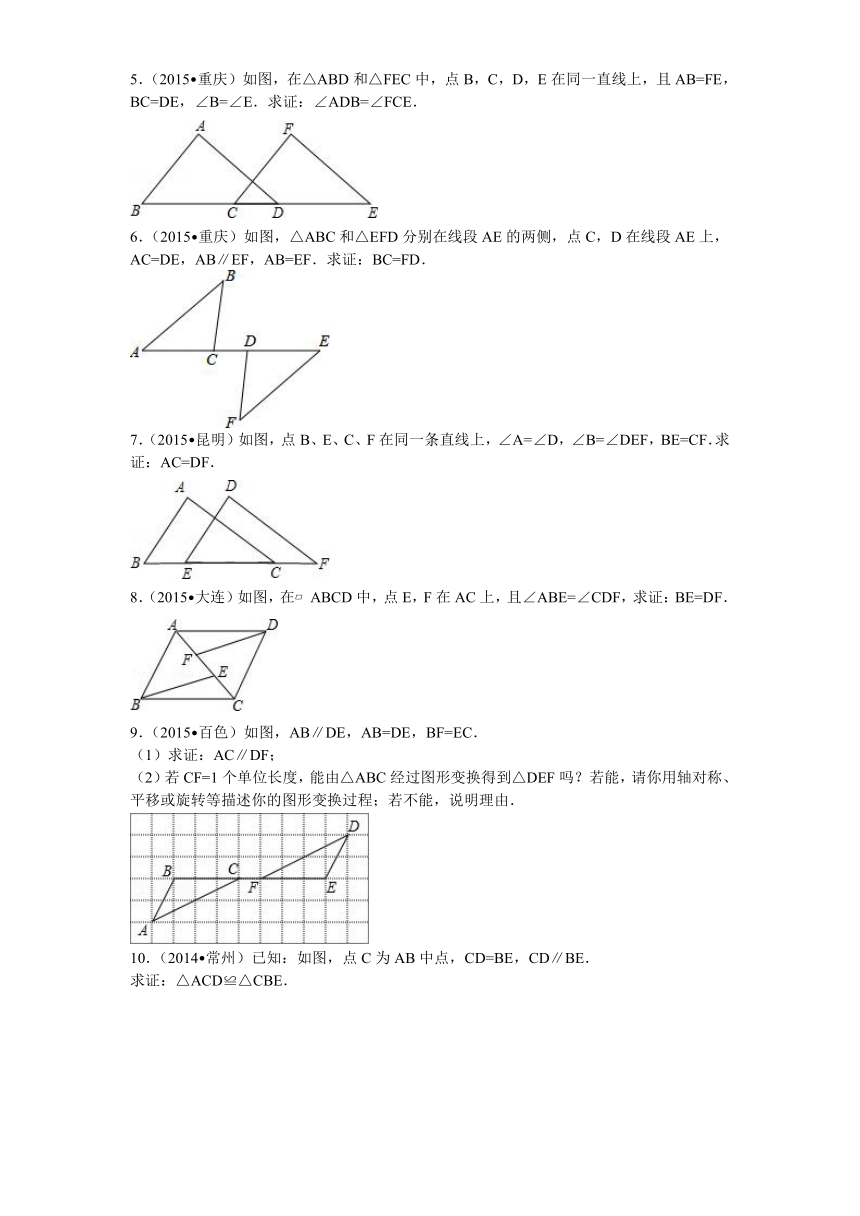
2．（2015 温州）如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D．
（1）求证：AB=CD．
（2）若AB=CF，∠B=30°，求∠D的度数．
( http: / / www.21cnjy.com )
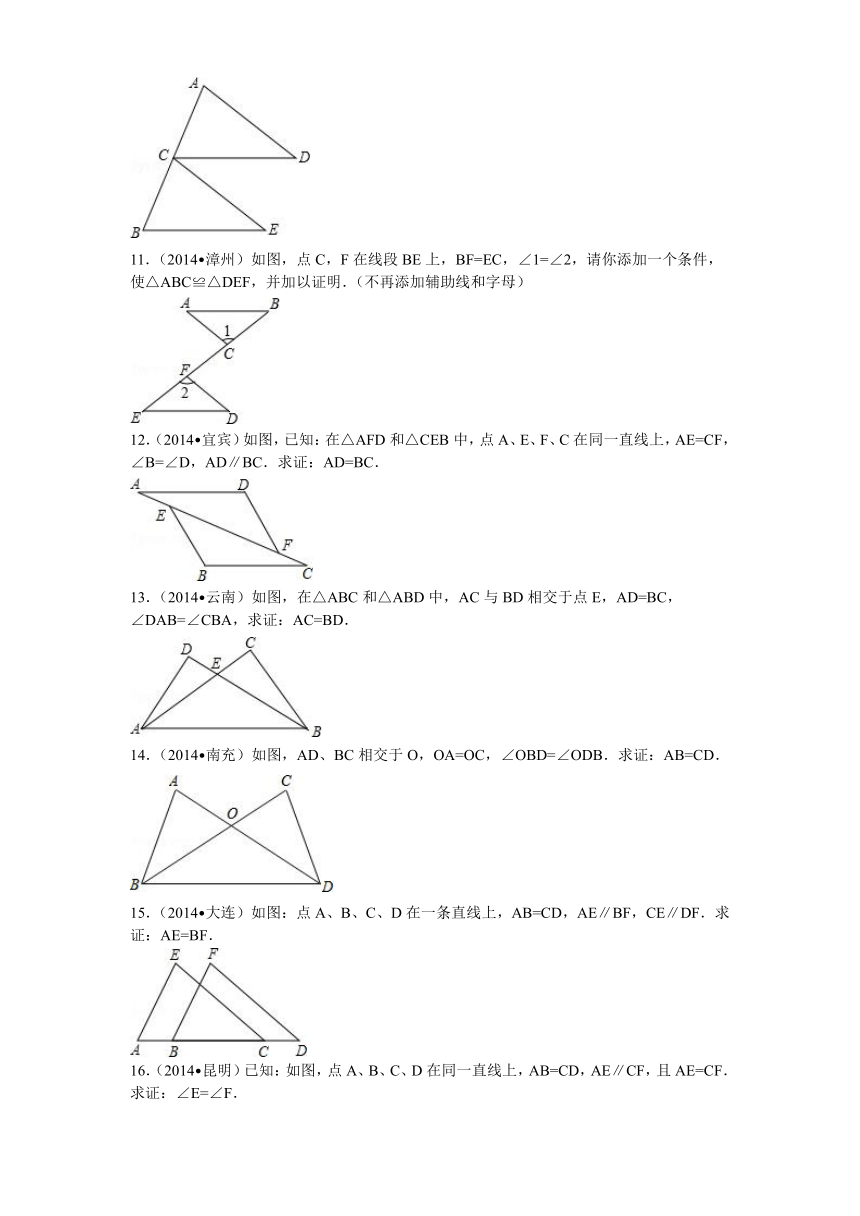
3．（2015 武汉）如图，点B、C、E、F在同一直线上，BC=EF，AC⊥BC于点C，DF⊥EF于点F，AC=DF．求证：
（1）△ABC≌△DEF；
（2）AB∥DE．
( http: / / www.21cnjy.com )
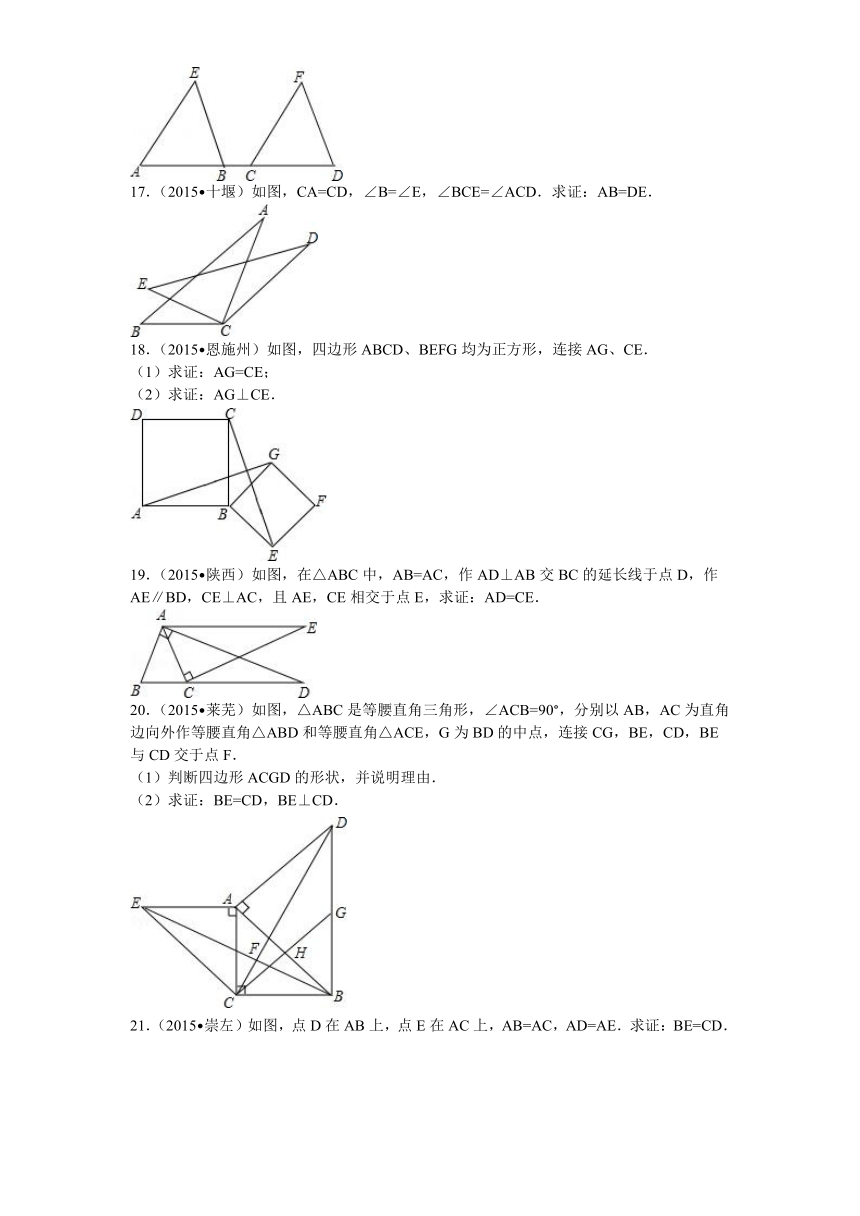
4．（2015 梅州）如图，已知△ABC，按如下步骤作图：
①以A为圆心，AB长为半径画弧；
②以C为圆心，CB长为半径画弧，两弧相交于点D；
③连接BD，与AC交于点E，连接AD，CD．
（1）求证：△ABC≌△ADC；
（2）若∠BAC=30°，∠BCA=45°，AC=4，求BE的长．
( http: / / www.21cnjy.com )
5．（2015 重庆）如图，在△ABD和 ( http: / / www.21cnjy.com )△FEC中，点B，C，D，E在同一直线上，且AB=FE，BC=DE，∠B=∠E．求证：∠ADB=∠FCE．
( http: / / www.21cnjy.com )
6．（2015 重庆）如图，△ABC和△E ( http: / / www.21cnjy.com )FD分别在线段AE的两侧，点C，D在线段AE上，AC=DE，AB∥EF，AB=EF．求证：BC=FD．
( http: / / www.21cnjy.com )
7．（2015 昆明）如图，点B、E、C、F在同一条直线上，∠A=∠D，∠B=∠DEF，BE=CF．求证：AC=DF．
( http: / / www.21cnjy.com )
8．（2015 大连）如图，在 ABCD中，点E，F在AC上，且∠ABE=∠CDF，求证：BE=DF．
( http: / / www.21cnjy.com )
9．（2015 百色）如图，AB∥DE，AB=DE，BF=EC．
（1）求证：AC∥DF；
（2）若CF=1个单位长度，能由△ABC经 ( http: / / www.21cnjy.com )过图形变换得到△DEF吗？若能，请你用轴对称、平移或旋转等描述你的图形变换过程；若不能，说明理由．
( http: / / www.21cnjy.com )
10．（2014 常州）已知：如图，点C为AB中点，CD=BE，CD∥BE．
求证：△ACD≌△CBE．
( http: / / www.21cnjy.com )
11．（2014 漳州）如 ( http: / / www.21cnjy.com )图，点C，F在线段BE上，BF=EC，∠1=∠2，请你添加一个条件，使△ABC≌△DEF，并加以证明．（不再添加辅助线和字母）
( http: / / www.21cnjy.com )
12．（2014 宜宾）如图，已知：在 ( http: / / www.21cnjy.com )△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF，∠B=∠D，AD∥BC．求证：AD=BC．
( http: / / www.21cnjy.com )
13．（2014 云南）如图，在△ABC和△ABD中，AC与BD相交于点E，AD=BC，∠DAB=∠CBA，求证：AC=BD．
( http: / / www.21cnjy.com )
14．（2014 南充）如图，AD、BC相交于O，OA=OC，∠OBD=∠ODB．求证：AB=CD．
( http: / / www.21cnjy.com )
15．（2014 大连）如图：点A、B、C、D在一条直线上，AB=CD，AE∥BF，CE∥DF．求证：AE=BF．
( http: / / www.21cnjy.com )
16．（2014 昆明）已知：如图，点A、B、C、D在同一直线上，AB=CD，AE∥CF，且AE=CF．
求证：∠E=∠F．
( http: / / www.21cnjy.com )
17．（2015 十堰）如图，CA=CD，∠B=∠E，∠BCE=∠ACD．求证：AB=DE．
( http: / / www.21cnjy.com )
18．（2015 恩施州）如图，四边形ABCD、BEFG均为正方形，连接AG、CE．
（1）求证：AG=CE；
（2）求证：AG⊥CE．
( http: / / www.21cnjy.com )
19．（2015 陕西）如图，在△ ( http: / / www.21cnjy.com )ABC中，AB=AC，作AD⊥AB交BC的延长线于点D，作AE∥BD，CE⊥AC，且AE，CE相交于点E，求证：AD=CE．
( http: / / www.21cnjy.com )
20．（2015 莱芜）如图，△A ( http: / / www.21cnjy.com )BC是等腰直角三角形，∠ACB=90°，分别以AB，AC为直角边向外作等腰直角△ABD和等腰直角△ACE，G为BD的中点，连接CG，BE，CD，BE与CD交于点F．
（1）判断四边形ACGD的形状，并说明理由．
（2）求证：BE=CD，BE⊥CD．
( http: / / www.21cnjy.com )
21．（2015 崇左）如图，点D在AB上，点E在AC上，AB=AC，AD=AE．求证：BE=CD．
( http: / / www.21cnjy.com )
22．（2014 吉林）如图，△ABC和△DAE中，∠BAC=∠DAE，AB=AE，AC=AD，连接BD，CE，求证：△ABD≌△AEC．
( http: / / www.21cnjy.com )
23．（2014 武汉）如图，AC和BD相交于点O，OA=OC，OB=OD．求证：DC∥AB．
( http: / / www.21cnjy.com )
24．（2014 苏州）如图，在Rt△ABC ( http: / / www.21cnjy.com )中，∠ACB=90°，点D、F分别在AB、AC上，CF=CB，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．
（1）求证：△BCD≌△FCE；
（2）若EF∥CD，求∠BDC的度数．
( http: / / www.21cnjy.com )
25．（2014 自贡）如图，四边形ABCD是正方形，BE⊥BF，BE=BF，EF与BC交于点G．
（1）求证：AE=CF；
（2）若∠ABE=55°，求∠EGC的大小．
( http: / / www.21cnjy.com )
26．（2014 宜昌）如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB．
（1）求∠CAD的度数；
（2）延长AC至E，使CE=AC，求证：DA=DE．
( http: / / www.21cnjy.com )
27．（2014 鄂州）在平面内正方形ABCD与正方形CEFH如图放置，连DE，BH，两线交于M．求证：
（1）BH=DE．
（2）BH⊥DE．
( http: / / www.21cnjy.com )
28．（2013 随州）如 ( http: / / www.21cnjy.com )图，点F、B、E、C在同一直线上，并且BF=CE，∠ABC=∠DEF．能否由上面的已知条件证明△ABC≌△DEF？如果能，请给出证明；如果不能，请从下列三个条件中选择一个合适的条件，添加到已知条件中，使△ABC≌△DEF，并给出证明．
提供的三个条件是：①AB=DE；②AC=DF；③AC∥DF．
( http: / / www.21cnjy.com )
29．（2013 仙桃） ( http: / / www.21cnjy.com )如图，已知△ABC≌△ADE，AB与ED交于点M，BC与ED，AD分别交于点F，N．请写出图中两对全等三角形（△ABC≌△ADE除外），并选择其中的一对加以证明．
( http: / / www.21cnjy.com )
　
参考答案
　
一．解答题（共29小题）
1．解：添加∠BAC=∠DAC．理由如下：
在△ABC与△ADC中，
，
∴△ABC≌△ADC（AAS）．
　
2．证明：（1）∵AB∥CD，
∴∠B=∠C，
在△ABE和△CDF中，
，
∴△ABE≌△CDF（AAS），
∴AB=CD；
（2）∵△ABE≌△CDF，
∴AB=CD，BE=CF，
∵AB=CF，∠B=30°，
∴AB=BE，
∴△ABE是等腰三角形，
∴∠D=．
　
3．证明：（1）∵AC⊥BC于点C，DF⊥EF于点F，
∴∠ACB=∠DFE=90°，
在△ABC和△DEF中，，
∴△ABC≌△DEF（SAS）；
（2）∵△ABC≌△DEF，
∴∠B=∠DEF，
∴AB∥DE．
　
4．（1）证明：在△ABC与△ADC中，
，
∴△ABC≌△ADC（SSS）；
（2）解：设BE=x，
∵∠BAC=30°，
∴∠ABE=60°，
∴AE=tan60° x=x，
∵△ABC≌△ADC，
∴CB=CD，∠BCA=∠DCA，
∵∠BCA=45°，
∴∠BCA=∠DCA=45°，
∴∠CBD=∠CDB=45°，
∴CE=BE=x，
∴x+x=4，
∴x=2﹣2，
∴BE=2﹣2．
　
5．证明：∵BC=DE，
∴BC+CD=DE+CD，
即BD=CE，
在△ABD与△FEC中，
，
∴△ABD≌△FEC（SAS），
∴∠ADB=∠FCE．
　
6．证明：∵AB∥EF，
∴∠A=∠E，
在△ABC和△EFD中
∴△ABC≌△EFD（SAS）
∴BC=FD．
　
7．证明：∵BF=EC（已知），
∴BF+FC=EC+CF，
即BC=EF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（AAS），
∴AC=DF（全等三角形对应边相等）．
　
8．证明：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
∴∠BAC=∠CDF，
∴△ABE和△CDF中，
，
∴△ABE≌△CDF，
∴BE=DF．
　
9．解：（1）∵AB∥DE，
∴∠B=∠E，
∵BF=CE，
∴BF﹣FC=CE﹣FC，
即BC=EF，
∵在△ABC和△DEF中，
，
∴△ABC≌△DEF（SAS），
∴∠ACB=∠DFE，
∴∠ACF=∠DFC，
∴AC∥DF；
（2）△ABC先向右平移1个单位长度，再绕点C旋转180°即可得到△DEF．
　
10．证明：∵C是AB的中点（已知），
∴AC=CB（线段中点的定义）．
∵CD∥BE（已知），
∴∠ACD=∠B（两直线平行，同位角相等）．
在△ACD和△CBE中，
，
∴△ACD≌△CBE（SAS）．
　
11． AC=DF．
证明：∵BF=EC，
∴BF﹣CF=EC﹣CF，
∴BC=EF，
在△ABC和△DEF中
∴△ABC≌△DEF（SAS）．
　
12．证明：∵AD∥BC，
∴∠A=∠C，
∵AE=CF，
∴AE+EF=CF+EF，
即AF=CE，
∵在△ADF和△CBE中
，
∴△ADF≌△CBE（AAS），
∴AD=BC．
　
13．证明：在△ADB和△BAC中，
，
∴△ADB≌△BAC（SAS），
∴AC=BD．
　
14．证明：∵∠OBD=∠ODB，
∴OB=OD，
在△ABO和△CDO中，
，
∴△ABO≌△CDO（SAS），
∴AB=CD．
　
15．证明：∵AE∥BF，
∴∠A=∠FBD，
∵CE∥DF，
∴∠D=∠ACE，
∵AB=CD，
∴AB+BC=CD+BC，
即AC=BD，
在△ACE和△BDF中，
，
∴△ACE≌△BDF（ASA），
∴AE=BF．
　
16．证明：∵AE∥CF，
∴∠A=∠FCD，
在△ABE和△CDF中，
，
∴△ABE≌△CDF（SAS），
∴∠E=∠F．
　
17．解：如图，∵∠BCE=∠ACD，
∴∠ACB=∠DCE；在△ABC与△DEC中，
，
∴△ABC≌△DEC（AAS），
∴AB=DE．
( http: / / www.21cnjy.com )
　
18．（1）证明：∵四边形ABCD、BEFG均为正方形，
∴AB=CB，∠ABC=∠GBE=90°，BG=BE，
∴∠ABG=∠CBE，
在△ABG和△CBE中，，
∴△ABG≌△CBE（SAS），
∴AG=CE；
（2）证明：如图所示：∵△ABG≌△CBE，
∴∠BAG=∠BCE，
∵∠ABC=90°，
∴∠BAG+∠AMB=90°，
∵∠AMB=∠CMN，
∴∠BCE+∠CMN=90°，
∴∠CNM=90°，
∴AG⊥CE．
( http: / / www.21cnjy.com )
　
19．证明：∵AE∥BD，
∴∠EAC=∠ACB，
∵AB=AC，
∴∠B=∠ACB，
∴∠B=∠EAC，
在△ABD和△CAE中，
，
∴△ABD≌△CAE，
∴AD=CE．
　
20．（1）解：∵△ABC是等腰直角三角形，∠ACB=90°，
∴AB=BC，
∵△ABD和△ACE均为等腰直角三角形，
∴BD==BC=2BC，
∵G为BD的中点，
∴BG=BD=BC，
∴△CBG为等腰直角三角形，
∴∠CGB=45°，
∵∠ADB=45°，
AD∥CG，
∵∠ABD=45°，∠ABC=45°
∴∠CBD=90°，
∵∠ACB=90°，
∴∠CBD+∠ACB=180°，
∴AC∥BD，
∴四边形ACGD为平行四边形；
（2）证明：∵∠EAB=∠EAC+∠CAB=90°+45°=135°，
∠CAD=∠DAB+∠BAC=90°+45°=135°，
∴∠EAB=∠CAD，
在△DAC与△BAE中，
，
∴△DAC≌△BAE，
∴BE=CD；
∵∠EAC=∠BCA=90°，EA=AC=BC，
∴四边形ABCE为平行四边形，
∴CE=AB=AD，
在△BCE与△CAD中，
，
∴△BCE≌△CAD，
∴∠CBE=∠ACD，
∵∠ACD+∠BCD=90°，
∴∠CBE+∠BCD=90°，
∴∠CFB=90°，
即BE⊥CD．
( http: / / www.21cnjy.com )
　
21．解：在△ADC和△AEB中，
∵，
∴△ADC≌△AEB，
∴BE=CD．
　
22．证明：∵∠BAC=∠DAE，
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE，
即∠BAD=∠CAE，
在△ABD和△AEC中，
，
∴△ABD≌△AEC（SAS）．
　
23．证明：∵在△ODC和△OBA中，
∵，
∴△ODC≌△OBA（SAS），
∴∠C=∠A（或者∠D=∠B）（全等三角形对应角相等），
∴DC∥AB（内错角相等，两直线平行）．
　
24．（1）证明：∵将线段CD绕点C按顺时针方向旋转90°后得CE，
∴CD=CE，∠DCE=90°，
∵∠ACB=90°，
∴∠BCD=90°﹣∠ACD=∠FCE，
在△BCD和△FCE中，
，
∴△BCD≌△FCE（SAS）．
（2）解：由（1）可知△BCD≌△FCE，
∴∠BDC=∠E，∠BCD=∠FCE，
∴∠DCE=∠DCA+∠FCE=∠DCA+∠BCD=∠ACB=90°，
∵EF∥CD，
∴∠E=180°﹣∠DCE=90°，
∴∠BDC=90°．
　
25．（1）证明：∵四边形ABCD是正方形，
∴∠ABC=90°，AB=BC，
∵BE⊥BF，
∴∠FBE=90°，
∵∠ABE+∠EBC=90°，∠CBF+∠EBC=90°，
∴∠ABE=∠CBF，
在△AEB和△CFB中，
∴△AEB≌△CFB（SAS），
∴AE=CF．
（2）解：∵BE⊥BF，
∴∠FBE=90°，
又∵BE=BF，
∴∠BEF=∠EFB=45°，
∵四边形ABCD是正方形，
∴∠ABC=90°，
又∵∠ABE=55°，
∴∠EBG=90°﹣55°=35°，
∴∠EGC=∠EBG+∠BEF=45°+35°=80°．
( http: / / www.21cnjy.com )
　
26．（1）解：如图，∵在Rt△ABC中，∠ACB=90°，∠B=30°，
∴∠B=30°，
∴∠CAB=60°．
又∵AD平分∠CAB，
∴∠CAD=∠CAB=30°，即∠CAD=30°；
（2）证明：∵∠ACD+∠ECD=180°，且∠ACD=90°，
∴∠ECD=90°，
∴∠ACD=∠ECD．
在△ACD与△ECD中，
，
∴△ACD≌△ECD（SAS），
∴DA=DE．
　
27．证明：（1）在正方形ABCD与正方形CEFH中，
BC=CD，CE=CH，∠BCD=∠ECH=90°，
∴∠BCD+∠DCH=∠ECH+∠DCH，
即∠BCH=∠DCE，
在△BCH和△DCE中，
，
∴△BCH≌△DCE（SAS），
∴BH=DE；
（2）∵△BCH≌△DCE，
∴∠CBH=∠CDE，
又∵∠CGB=∠MGD，
∴∠DMB=∠BCD=90°，
∴BH⊥DE．
( http: / / www.21cnjy.com )
　
28．解：不能；
选择条件：①AB=DE；
∵BF=CE，
∴BF+BE=CE+BE，
即EF=CB，
在△ABC和△DFE中，
∴△ABC≌△DFE（SAS）．
　
29．解：△AEM≌△ACN，△BMF≌△DNF，△ABN≌△ADM．
选择△AEM≌△ACN，
理由如下：
∵△ADE≌△ABC，
∴AE=AC，∠E=∠C，∠EAD=∠CAB，
∴∠EAM=∠CAN，
∵在△AEM和△ACN中，
∴△AEM≌△ACN（ASA）．