第17章 勾股定理 综合测试题(含解析)2024-2025学年人教版数学八年级下册
文档属性
| 名称 | 第17章 勾股定理 综合测试题(含解析)2024-2025学年人教版数学八年级下册 |  | |
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 16:00:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第17章 勾股定理 综合测试题
一.选择题
1.下列各组数据为勾股数的是( )
A.1,2,3 B. C.9,40,41 D.,,
2.在下列条件中,不能判断△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.AB=3,BC=4,
C.AB=AC,∠B=45° D.∠A=30°,
3.平面直角坐标系中,已知A(2,3),B(﹣2,﹣14),C(4,6),D(﹣1,﹣7)四点,则下列结论正确的是( )
A.AC=2BD B.CD=2AB C.AD=2BC D.BC=2AD
4.如图,在Rt△ABC中,∠ACB=90°,,AC=2.D为斜边AB上一动点,连接CD,过点D作DE⊥CD交边BC于点E,若△BDE为等腰三角形,则△CDE的周长为( )
A. B.6 C. D.5
5.如图,在Rt△ABC中,∠ACB=90°,分别以A点,B点为圆心,以大于为半径画弧,两弧交于E,F,连接EF交AB于点D,交AC于点H.连接CD,以C为圆心,CD长为半径作弧,交AC于G点,若AB=10cm,BC=6cm,则GH的长度为( )
A. B. C.3cm D.
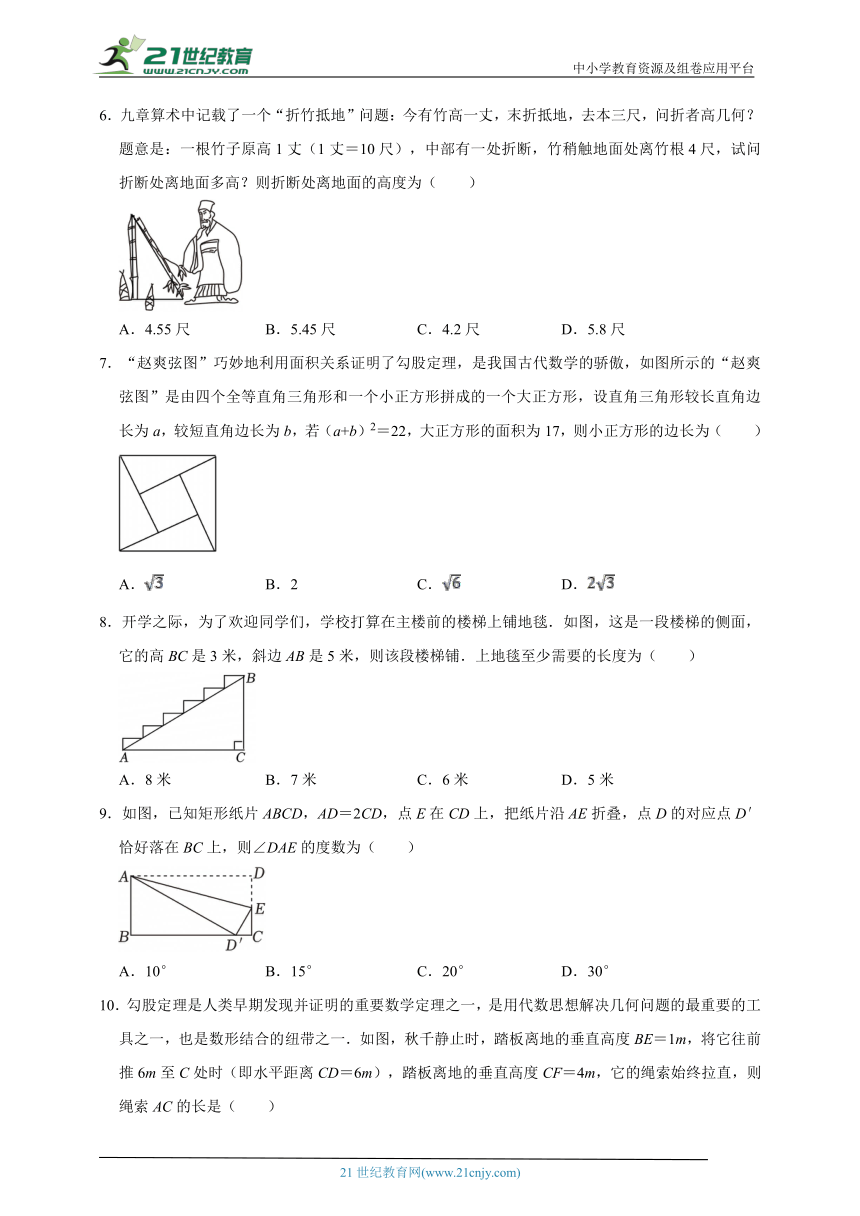
6.九章算术中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?题意是:一根竹子原高1丈(1丈=10尺),中部有一处折断,竹稍触地面处离竹根4尺,试问折断处离地面多高?则折断处离地面的高度为( )
A.4.55尺 B.5.45尺 C.4.2尺 D.5.8尺
7.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=22,大正方形的面积为17,则小正方形的边长为( )
A. B.2 C. D.
8.开学之际,为了欢迎同学们,学校打算在主楼前的楼梯上铺地毯.如图,这是一段楼梯的侧面,它的高BC是3米,斜边AB是5米,则该段楼梯铺.上地毯至少需要的长度为( )
A.8米 B.7米 C.6米 D.5米
9.如图,已知矩形纸片ABCD,AD=2CD,点E在CD上,把纸片沿AE折叠,点D的对应点D′恰好落在BC上,则∠DAE的度数为( )
A.10° B.15° C.20° D.30°
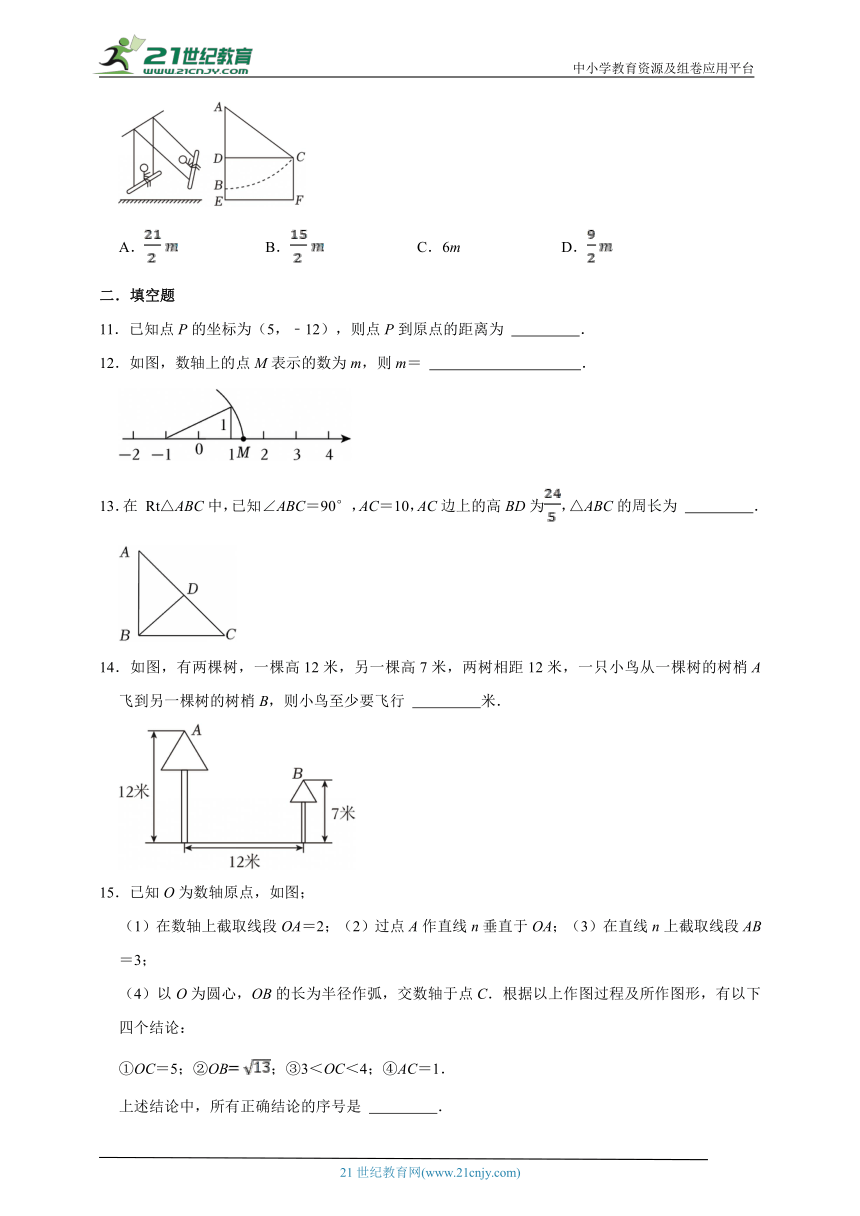
10.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.如图,秋千静止时,踏板离地的垂直高度BE=1m,将它往前推6m至C处时(即水平距离CD=6m),踏板离地的垂直高度CF=4m,它的绳索始终拉直,则绳索AC的长是( )
A. B. C.6m D.
二.填空题
11.已知点P的坐标为(5,﹣12),则点P到原点的距离为 .
12.如图,数轴上的点M表示的数为m,则m= .
13.在 Rt△ABC中,已知∠ABC=90°,AC=10,AC边上的高BD为,△ABC的周长为 .
14.如图,有两棵树,一棵高12米,另一棵高7米,两树相距12米,一只小鸟从一棵树的树梢A飞到另一棵树的树梢B,则小鸟至少要飞行 米.
15.已知O为数轴原点,如图;
(1)在数轴上截取线段OA=2;(2)过点A作直线n垂直于OA;(3)在直线n上截取线段AB=3;
(4)以O为圆心,OB的长为半径作弧,交数轴于点C.根据以上作图过程及所作图形,有以下四个结论:
①OC=5;②OB;③3<OC<4;④AC=1.
上述结论中,所有正确结论的序号是 .
三.解答题
16.如图,在四边形ABCD中,∠B=90°,,,DA=1,CD=3,
(1)证明△ACD是直角三角形;
(2)求四边形ABCD的面积.
17.如图,四边形ABCD中,∠ABC=∠DCB,对角线AC,BD相交于点O,且BD垂直平分AC,过A点作AE∥CD交BC点E.
(1)求证:AE=BC;
(2)若BE=2,,求EC的长度.
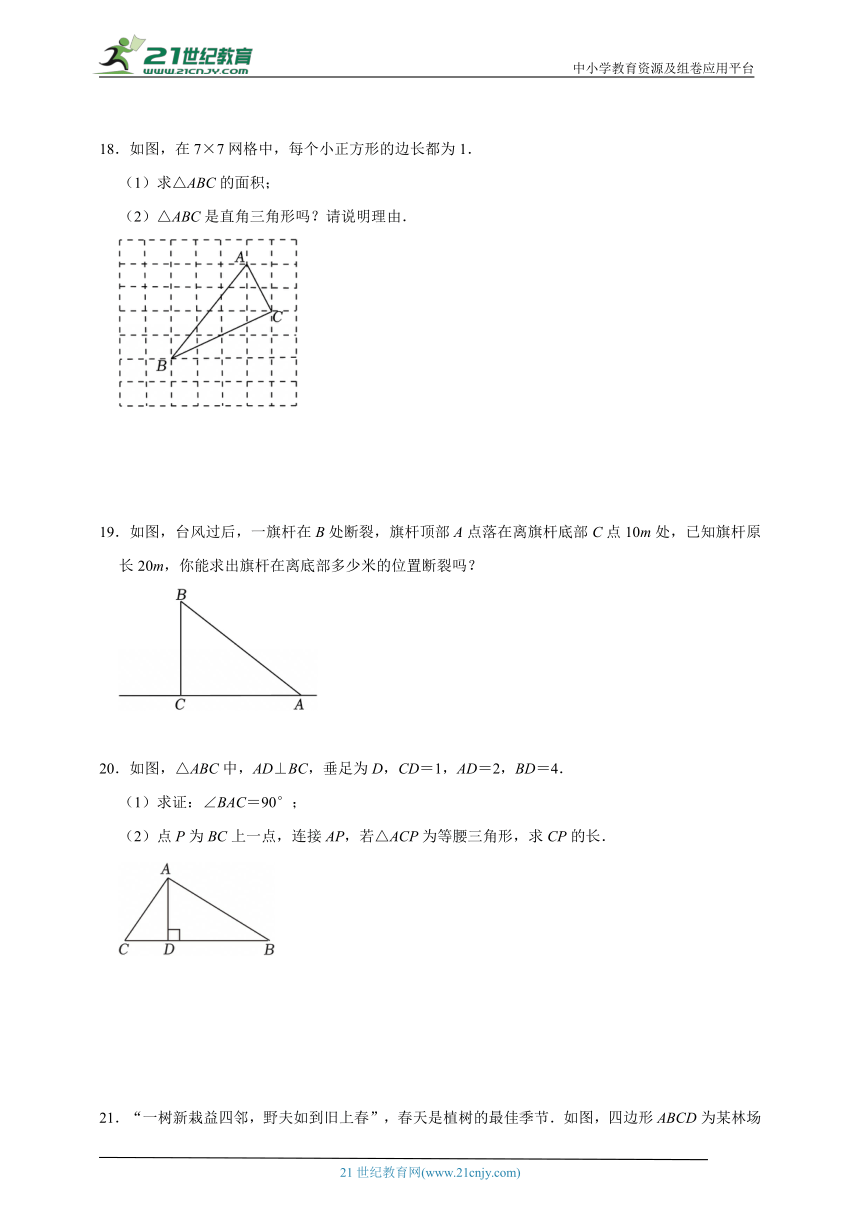
18.如图,在7×7网格中,每个小正方形的边长都为1.
(1)求△ABC的面积;
(2)△ABC是直角三角形吗?请说明理由.
19.如图,台风过后,一旗杆在B处断裂,旗杆顶部A点落在离旗杆底部C点10m处,已知旗杆原长20m,你能求出旗杆在离底部多少米的位置断裂吗?
20.如图,△ABC中,AD⊥BC,垂足为D,CD=1,AD=2,BD=4.
(1)求证:∠BAC=90°;
(2)点P为BC上一点,连接AP,若△ACP为等腰三角形,求CP的长.
21.“一树新栽益四邻,野夫如到旧上春”,春天是植树的最佳季节.如图,四边形ABCD为某林场种植树林的区域,AB⊥BC.经测量AB=9km,BC=12km,CD=8km,AD=17km.
(1)护林员操控一架无人机从A处沿直线飞行到C处进行巡查,求无人机飞行路径AC的长;
(2)证明:AC⊥CD.
22.满足a2+b2=c2的三个正整数,称为勾股数.
(1)请把下列三组勾股数补充完整:① ,8,10;②9, ,15;③9,40, .
(2)小明发现,很多已经约去公因数的勾股数组中,都有一个数是偶数,如果将它写成2mn,那么另外两个数可以写成m2+n2,m2﹣n2,如4=2×2×1,5=22+12,3=22﹣12,请你帮小明证明这三个数2mn,m2+n2,m2﹣n2是勾股数组.
(3)如果28,96,100是满足上述小明发现的规律的勾股数组,则m+n= .
23.△ABC中,BC=a,AC=b,AB=c.若∠C=90°,如图1,根据勾股定理,则a2+b2=c2.若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.
参考答案
一.选择题
1.解:A、1+2=3,不能构成三角形,该选项不符合题意;
B、不是正整数,1,,2不是勾股数,该选项不符合题意;
C、92+402=412,9,40,41是勾股数,该选项符合题意;
D、()2+()2≠()2,,,不是勾股数,该选项不符合题意;
选:C.
2.解:A、∵∠A=40°,∠B=50°,
∴∠C=180°﹣40°﹣50°=90°,
∴△ABC是直角三角形,不符合题意;
B、∵AB=3,BC=4,,
∴AB2+AC2=BC2,
∴∠A=90°,
∴△ABC是直角三角形,不符合题意;
C、∵AB=AC,∠B=45°,
∴∠B=∠C=45°,
∴∠A=90°,
∴△ABC是直角三角形,不符合题意.
D、不能得出△ABC是直角三角形,符合题意,
选:D.
3.解:A、∵,,
∴AC≠2BD,A选项不符合题意;
B、∵,,
∴CD≠2AB,B选项不符合题意;
C、∵,,
∴AD≠2BC,C选项不符合题意;
D、∵,
∴BC=2AD,D选项符合题意;
选:D.
4.解:由题意,∵∠DEB是△CDE的一个外角,
∴∠DEB=∠CDE+∠DCE=90°+∠DCE.
∴∠DEB是钝角.
又△BDE为等腰三角形,
∴BE=DE.
∴∠B=∠BDE.
∵∠ACB=∠CDE=90°,
∴∠B+∠BAC=90°,∠BDE+∠CDA=90°.
∴∠BAC=∠CDA.
∴CA=CD=2.
在Rt△ACB中,∠ACB=90°,
∴BC3.
∴BC=BE+CE=DE+CE=3.
又△CDE的周长=CD+DE+CE,
∴△CDE的周长=2+3=5.
选:D.
5.解:连接BH,如图所示:
根据作图可知,EF垂直平分AB,
∴BH=AH,AD=BD,
∵△ABC为直角三角形,
∴,
∴CG=CD=5cm,
根据勾股定理得:,
∴AG=AC﹣CG=8﹣5=3(cm),
设AH=BH=x cm,则CH=(8﹣x)cm,
根据勾股定理得:BC2+CH2=BH2,
即62+(8﹣x)2=x2,
解得:,
∴,
选:B.
6.解:设折断处离地面的高度AB为x尺,则AC=(10﹣x)尺,
在Rt△ABC中,由勾股定理得:AB2+BC2=AC2,
∴x2+42=(10﹣x)2,
解得:x=4.2,
即折断处离地面的高度为4.2尺,
选:C.
7.解:如图所示,由题意,ED=a,AE=b,
∵大正方形的面积为17,
∴AD2=17,
∵AD2=AE2+ED2=a2+b2,
∴a2+b2=17,
∵(a+b)2=22,
∴(a﹣b)2=2(a2+b2)﹣(a+b)2=2×17﹣22=12,
∵EF=ED﹣EF=a﹣b,
∴小正方形的边长为EF=2(负值舍去),
选:D.
8.解:在直角三角形ABC中,高BC是3米,斜边AB长是5米,
由勾股定理得AC4(米),
根据题意,台阶的高的和为BC,宽的和为AC,
AC+BC=7米,
选:B.
9.解:∵四边形ABCD是矩形,
∴∠ABD'=90°,AB=CD,AD∥BC,
∵AD'由AD翻折得到,AD=2CD,
∴AD'=2AB,∠DAE=∠D'AE∠DAD',
∵sin∠AD'B,
∴∠AD'B=30°,
∵AD∥BC,
∴∠DAD'=∠AD'B=30°,
∴∠DAE=15°.
选:B.
10.解:设AC=AB=x m.
∵四边形EFCD是矩形,
∴CF=DE=4m,
∵BE=1m,
∴AD=AE﹣BE=x+1﹣4=(x﹣3)m,
在Rt△ADC中,AC2=AD2+CD2,
∴x2=(x﹣3)2+62,
解得x,
∴ACm.
选:B.
二.填空题
11.解:∵点P的坐标为(5,﹣12),
∴点P到原点的距离OP13,
答案为:13.
12.解:根据题意得:,
答案为:.
13.解:∵∠ABC=90°,AC=10,AC边上的高BD为,
∴S△ABCAB BCAC BD,
∴AB BC=1048,
∴(AB+BC)2=AB2+BC2+2AB BC=AC2+2×48=100+96=196,
∴AB+BC=14,
∴△ABC的周长=14+10=24,
答案为:24.
14.解:过B作BC∥地面,连接AB,
,
由题意得,BC=12米,AC=12﹣7=5(米),
由勾股定理得,AB13(米),
答案为:13.
15.解:根据题意得,OA=2,AB=3,∠OAB=90°,
∴OB,
②正确;
∵OC=OB,
∴OC,
∴③正确,①错误;
∴AC=OC﹣OA2≠1,
④错误;
答案为:②③.
三.解答题
16.(1)证明:∵AC=2,DA=1,CD=3,
∴AC2+DA2=8+1=9,CD2=9,
∴AC2+DA2=CD2,
∴△ACD是直角三角形,且∠CAD=90°,
(2)解:∵∠B=90°,AC=2,BC,
∴AB,
∴四边形ABCD的面积=△ABC的面积+△ACD的面积
AB BCAC AD
1×2
.
答案为:.
17.(1)证明:∵AE∥CD,
∴∠AEB=∠DCB,
∵∠ABC=∠DCB,
∴∠ABC=∠AEB,
∴AB=AE,
∵BD垂直平分AC,
∴AB=BC,
∴AE=BC;
(2)解:过点A作AF⊥BE于点F,
∵AB=AE,
∴BF=EFBE=1,
在Rt△ABF和Rt△ACF中,
AB2﹣BF2=AF2=AC2﹣CF2,
∵AB=AE=BC=2+CE,CF=EF+CE=1+CE,
∴(2+CE)2﹣12(1+CE)2,
∴CE=1(负值已舍),
∴EC的长度为1.
18.解:(1)S△ABC=4×44×23×41×2
=16﹣4﹣6﹣1
=5;
(2)∵AC2=22+12=5,BC2=22+42=20,AB2=42+32=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
19.解:设旗杆断裂处距离C点x m,则BC=x m,AB=(20﹣x)m,
在Rt△ABC中,AC=10m,
由勾股定理得:AB2=AC2+BC2
即x2+102=(20﹣x)2
解得:x=7.5
答:旗杆在离底部7.5米的位置断裂.
20.(1)证明:∵AD⊥BC,
∴∠ADC=∠ADB=90°,
在Rt△ACD中,CD=1,AD=2,
∴AC,
在Rt△ABD中,BD=4,
∴AB2,
在△ABC中,AC2+AB2=()2+(2)2=25,
BC2=(CD+BD)2=52=25,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,
∴∠BAC=90°;
(2)解:分三种情况:
当CA=CP时,如图:
∴CP的长为;
当AC=AP时,如图:
∵AC=AP,AD⊥CP,
∴CP=2CD=2,
∴CP的长为2;
当PA=PC时,如图:
∵PA=PC,
∴∠C=∠PAC,
∵∠C+∠B=90°,∠PAC+∠PAB=90°,
∴∠B=∠PAB,
∴AP=BP,
∴CP=BPBC=2.5,
∴CP的长为2.5;
综上所述:CP的长为,2或2.5.
21.(1)解:在Rt△ABC中,由勾股定理得:AC15(km),
答:无人机飞行路径AC的长为15km;
(2)证明:∵AD2=172=289(km2),CD2+AC2=82+152=289(km2),
∴AD2=CD2+AC2,
∴△ACD是直角三角形,且∠ACD=90°,
∴AC⊥CD.
22.(1)解:①设空缺的数为x,
则有三种情况:x2+82=102,x2+102=82,102+82=x2,
解得:x=±6,,
∵x要为正整数,
∴仅有x=6满足题意,
同理,对于②③,可求得空缺的数为:12,41,
答案为:6,12,41;
(2)证明:(2mn)2=4m2n2,
(m2+n2)2=m4+2m2n2+n4,
(m2﹣n2)2=m4﹣2m2n2+n4,
显然,m4+2m2n2+n4=m4﹣2m2n2+n4+4m2n2,
即:(m2+n2)2=(m2﹣n2)2+(2mn)2,
∴2mn,m2+n2,m2﹣n2是勾股数组;
(3)解:28,96,100约去公因数4,得到7,24,25,
其中,24=2×3×4,
∵25=42+32,7=42﹣32,
∴m=4,n=3,
∴m+n=7,
答案为:7.
23.解:若△ABC是锐角三角形,则有a2+b2>c2(1分)
若△ABC是钝角三角形,∠C为钝角,则有a2+b2<c2.(2分)
当△ABC是锐角三角形时,
证明:过点A作AD⊥BC,垂足为D,设CD为x,则有BD=a﹣x(3分)
根据勾股定理,得b2﹣x2=AD2=c2﹣(a﹣x)2
即b2﹣x2=c2﹣a2+2ax﹣x2.
∴a2+b2=c2+2ax(5分)
∵a>0,x>0,
∴2ax>0.
∴a2+b2>c2.(6分)
当△ABC是钝角三角形时,
证明:过B作BD⊥AC,交AC的延长线于D.
设CD为y,则有BD2=a2﹣y2(7分)
根据勾股定理,得(b+y)2+a2﹣y2=c2.
即a2+b2+2by=c2.(9分)
∵b>0,y>0,
∴2by>0,
∴a2+b2<c2.(10分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第17章 勾股定理 综合测试题
一.选择题
1.下列各组数据为勾股数的是( )
A.1,2,3 B. C.9,40,41 D.,,
2.在下列条件中,不能判断△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.AB=3,BC=4,
C.AB=AC,∠B=45° D.∠A=30°,
3.平面直角坐标系中,已知A(2,3),B(﹣2,﹣14),C(4,6),D(﹣1,﹣7)四点,则下列结论正确的是( )
A.AC=2BD B.CD=2AB C.AD=2BC D.BC=2AD
4.如图,在Rt△ABC中,∠ACB=90°,,AC=2.D为斜边AB上一动点,连接CD,过点D作DE⊥CD交边BC于点E,若△BDE为等腰三角形,则△CDE的周长为( )
A. B.6 C. D.5
5.如图,在Rt△ABC中,∠ACB=90°,分别以A点,B点为圆心,以大于为半径画弧,两弧交于E,F,连接EF交AB于点D,交AC于点H.连接CD,以C为圆心,CD长为半径作弧,交AC于G点,若AB=10cm,BC=6cm,则GH的长度为( )
A. B. C.3cm D.
6.九章算术中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?题意是:一根竹子原高1丈(1丈=10尺),中部有一处折断,竹稍触地面处离竹根4尺,试问折断处离地面多高?则折断处离地面的高度为( )
A.4.55尺 B.5.45尺 C.4.2尺 D.5.8尺
7.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=22,大正方形的面积为17,则小正方形的边长为( )
A. B.2 C. D.
8.开学之际,为了欢迎同学们,学校打算在主楼前的楼梯上铺地毯.如图,这是一段楼梯的侧面,它的高BC是3米,斜边AB是5米,则该段楼梯铺.上地毯至少需要的长度为( )
A.8米 B.7米 C.6米 D.5米
9.如图,已知矩形纸片ABCD,AD=2CD,点E在CD上,把纸片沿AE折叠,点D的对应点D′恰好落在BC上,则∠DAE的度数为( )
A.10° B.15° C.20° D.30°
10.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.如图,秋千静止时,踏板离地的垂直高度BE=1m,将它往前推6m至C处时(即水平距离CD=6m),踏板离地的垂直高度CF=4m,它的绳索始终拉直,则绳索AC的长是( )
A. B. C.6m D.
二.填空题
11.已知点P的坐标为(5,﹣12),则点P到原点的距离为 .
12.如图,数轴上的点M表示的数为m,则m= .
13.在 Rt△ABC中,已知∠ABC=90°,AC=10,AC边上的高BD为,△ABC的周长为 .
14.如图,有两棵树,一棵高12米,另一棵高7米,两树相距12米,一只小鸟从一棵树的树梢A飞到另一棵树的树梢B,则小鸟至少要飞行 米.
15.已知O为数轴原点,如图;
(1)在数轴上截取线段OA=2;(2)过点A作直线n垂直于OA;(3)在直线n上截取线段AB=3;
(4)以O为圆心,OB的长为半径作弧,交数轴于点C.根据以上作图过程及所作图形,有以下四个结论:
①OC=5;②OB;③3<OC<4;④AC=1.
上述结论中,所有正确结论的序号是 .
三.解答题
16.如图,在四边形ABCD中,∠B=90°,,,DA=1,CD=3,
(1)证明△ACD是直角三角形;
(2)求四边形ABCD的面积.
17.如图,四边形ABCD中,∠ABC=∠DCB,对角线AC,BD相交于点O,且BD垂直平分AC,过A点作AE∥CD交BC点E.
(1)求证:AE=BC;
(2)若BE=2,,求EC的长度.
18.如图,在7×7网格中,每个小正方形的边长都为1.
(1)求△ABC的面积;
(2)△ABC是直角三角形吗?请说明理由.
19.如图,台风过后,一旗杆在B处断裂,旗杆顶部A点落在离旗杆底部C点10m处,已知旗杆原长20m,你能求出旗杆在离底部多少米的位置断裂吗?
20.如图,△ABC中,AD⊥BC,垂足为D,CD=1,AD=2,BD=4.
(1)求证:∠BAC=90°;
(2)点P为BC上一点,连接AP,若△ACP为等腰三角形,求CP的长.
21.“一树新栽益四邻,野夫如到旧上春”,春天是植树的最佳季节.如图,四边形ABCD为某林场种植树林的区域,AB⊥BC.经测量AB=9km,BC=12km,CD=8km,AD=17km.
(1)护林员操控一架无人机从A处沿直线飞行到C处进行巡查,求无人机飞行路径AC的长;
(2)证明:AC⊥CD.
22.满足a2+b2=c2的三个正整数,称为勾股数.
(1)请把下列三组勾股数补充完整:① ,8,10;②9, ,15;③9,40, .
(2)小明发现,很多已经约去公因数的勾股数组中,都有一个数是偶数,如果将它写成2mn,那么另外两个数可以写成m2+n2,m2﹣n2,如4=2×2×1,5=22+12,3=22﹣12,请你帮小明证明这三个数2mn,m2+n2,m2﹣n2是勾股数组.
(3)如果28,96,100是满足上述小明发现的规律的勾股数组,则m+n= .
23.△ABC中,BC=a,AC=b,AB=c.若∠C=90°,如图1,根据勾股定理,则a2+b2=c2.若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.
参考答案
一.选择题
1.解:A、1+2=3,不能构成三角形,该选项不符合题意;
B、不是正整数,1,,2不是勾股数,该选项不符合题意;
C、92+402=412,9,40,41是勾股数,该选项符合题意;
D、()2+()2≠()2,,,不是勾股数,该选项不符合题意;
选:C.
2.解:A、∵∠A=40°,∠B=50°,
∴∠C=180°﹣40°﹣50°=90°,
∴△ABC是直角三角形,不符合题意;
B、∵AB=3,BC=4,,
∴AB2+AC2=BC2,
∴∠A=90°,
∴△ABC是直角三角形,不符合题意;
C、∵AB=AC,∠B=45°,
∴∠B=∠C=45°,
∴∠A=90°,
∴△ABC是直角三角形,不符合题意.
D、不能得出△ABC是直角三角形,符合题意,
选:D.
3.解:A、∵,,
∴AC≠2BD,A选项不符合题意;
B、∵,,
∴CD≠2AB,B选项不符合题意;
C、∵,,
∴AD≠2BC,C选项不符合题意;
D、∵,
∴BC=2AD,D选项符合题意;
选:D.
4.解:由题意,∵∠DEB是△CDE的一个外角,
∴∠DEB=∠CDE+∠DCE=90°+∠DCE.
∴∠DEB是钝角.
又△BDE为等腰三角形,
∴BE=DE.
∴∠B=∠BDE.
∵∠ACB=∠CDE=90°,
∴∠B+∠BAC=90°,∠BDE+∠CDA=90°.
∴∠BAC=∠CDA.
∴CA=CD=2.
在Rt△ACB中,∠ACB=90°,
∴BC3.
∴BC=BE+CE=DE+CE=3.
又△CDE的周长=CD+DE+CE,
∴△CDE的周长=2+3=5.
选:D.
5.解:连接BH,如图所示:
根据作图可知,EF垂直平分AB,
∴BH=AH,AD=BD,
∵△ABC为直角三角形,
∴,
∴CG=CD=5cm,
根据勾股定理得:,
∴AG=AC﹣CG=8﹣5=3(cm),
设AH=BH=x cm,则CH=(8﹣x)cm,
根据勾股定理得:BC2+CH2=BH2,
即62+(8﹣x)2=x2,
解得:,
∴,
选:B.
6.解:设折断处离地面的高度AB为x尺,则AC=(10﹣x)尺,
在Rt△ABC中,由勾股定理得:AB2+BC2=AC2,
∴x2+42=(10﹣x)2,
解得:x=4.2,
即折断处离地面的高度为4.2尺,
选:C.
7.解:如图所示,由题意,ED=a,AE=b,
∵大正方形的面积为17,
∴AD2=17,
∵AD2=AE2+ED2=a2+b2,
∴a2+b2=17,
∵(a+b)2=22,
∴(a﹣b)2=2(a2+b2)﹣(a+b)2=2×17﹣22=12,
∵EF=ED﹣EF=a﹣b,
∴小正方形的边长为EF=2(负值舍去),
选:D.
8.解:在直角三角形ABC中,高BC是3米,斜边AB长是5米,
由勾股定理得AC4(米),
根据题意,台阶的高的和为BC,宽的和为AC,
AC+BC=7米,
选:B.
9.解:∵四边形ABCD是矩形,
∴∠ABD'=90°,AB=CD,AD∥BC,
∵AD'由AD翻折得到,AD=2CD,
∴AD'=2AB,∠DAE=∠D'AE∠DAD',
∵sin∠AD'B,
∴∠AD'B=30°,
∵AD∥BC,
∴∠DAD'=∠AD'B=30°,
∴∠DAE=15°.
选:B.
10.解:设AC=AB=x m.
∵四边形EFCD是矩形,
∴CF=DE=4m,
∵BE=1m,
∴AD=AE﹣BE=x+1﹣4=(x﹣3)m,
在Rt△ADC中,AC2=AD2+CD2,
∴x2=(x﹣3)2+62,
解得x,
∴ACm.
选:B.
二.填空题
11.解:∵点P的坐标为(5,﹣12),
∴点P到原点的距离OP13,
答案为:13.
12.解:根据题意得:,
答案为:.
13.解:∵∠ABC=90°,AC=10,AC边上的高BD为,
∴S△ABCAB BCAC BD,
∴AB BC=1048,
∴(AB+BC)2=AB2+BC2+2AB BC=AC2+2×48=100+96=196,
∴AB+BC=14,
∴△ABC的周长=14+10=24,
答案为:24.
14.解:过B作BC∥地面,连接AB,
,
由题意得,BC=12米,AC=12﹣7=5(米),
由勾股定理得,AB13(米),
答案为:13.
15.解:根据题意得,OA=2,AB=3,∠OAB=90°,
∴OB,
②正确;
∵OC=OB,
∴OC,
∴③正确,①错误;
∴AC=OC﹣OA2≠1,
④错误;
答案为:②③.
三.解答题
16.(1)证明:∵AC=2,DA=1,CD=3,
∴AC2+DA2=8+1=9,CD2=9,
∴AC2+DA2=CD2,
∴△ACD是直角三角形,且∠CAD=90°,
(2)解:∵∠B=90°,AC=2,BC,
∴AB,
∴四边形ABCD的面积=△ABC的面积+△ACD的面积
AB BCAC AD
1×2
.
答案为:.
17.(1)证明:∵AE∥CD,
∴∠AEB=∠DCB,
∵∠ABC=∠DCB,
∴∠ABC=∠AEB,
∴AB=AE,
∵BD垂直平分AC,
∴AB=BC,
∴AE=BC;
(2)解:过点A作AF⊥BE于点F,
∵AB=AE,
∴BF=EFBE=1,
在Rt△ABF和Rt△ACF中,
AB2﹣BF2=AF2=AC2﹣CF2,
∵AB=AE=BC=2+CE,CF=EF+CE=1+CE,
∴(2+CE)2﹣12(1+CE)2,
∴CE=1(负值已舍),
∴EC的长度为1.
18.解:(1)S△ABC=4×44×23×41×2
=16﹣4﹣6﹣1
=5;
(2)∵AC2=22+12=5,BC2=22+42=20,AB2=42+32=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
19.解:设旗杆断裂处距离C点x m,则BC=x m,AB=(20﹣x)m,
在Rt△ABC中,AC=10m,
由勾股定理得:AB2=AC2+BC2
即x2+102=(20﹣x)2
解得:x=7.5
答:旗杆在离底部7.5米的位置断裂.
20.(1)证明:∵AD⊥BC,
∴∠ADC=∠ADB=90°,
在Rt△ACD中,CD=1,AD=2,
∴AC,
在Rt△ABD中,BD=4,
∴AB2,
在△ABC中,AC2+AB2=()2+(2)2=25,
BC2=(CD+BD)2=52=25,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,
∴∠BAC=90°;
(2)解:分三种情况:
当CA=CP时,如图:
∴CP的长为;
当AC=AP时,如图:
∵AC=AP,AD⊥CP,
∴CP=2CD=2,
∴CP的长为2;
当PA=PC时,如图:
∵PA=PC,
∴∠C=∠PAC,
∵∠C+∠B=90°,∠PAC+∠PAB=90°,
∴∠B=∠PAB,
∴AP=BP,
∴CP=BPBC=2.5,
∴CP的长为2.5;
综上所述:CP的长为,2或2.5.
21.(1)解:在Rt△ABC中,由勾股定理得:AC15(km),
答:无人机飞行路径AC的长为15km;
(2)证明:∵AD2=172=289(km2),CD2+AC2=82+152=289(km2),
∴AD2=CD2+AC2,
∴△ACD是直角三角形,且∠ACD=90°,
∴AC⊥CD.
22.(1)解:①设空缺的数为x,
则有三种情况:x2+82=102,x2+102=82,102+82=x2,
解得:x=±6,,
∵x要为正整数,
∴仅有x=6满足题意,
同理,对于②③,可求得空缺的数为:12,41,
答案为:6,12,41;
(2)证明:(2mn)2=4m2n2,
(m2+n2)2=m4+2m2n2+n4,
(m2﹣n2)2=m4﹣2m2n2+n4,
显然,m4+2m2n2+n4=m4﹣2m2n2+n4+4m2n2,
即:(m2+n2)2=(m2﹣n2)2+(2mn)2,
∴2mn,m2+n2,m2﹣n2是勾股数组;
(3)解:28,96,100约去公因数4,得到7,24,25,
其中,24=2×3×4,
∵25=42+32,7=42﹣32,
∴m=4,n=3,
∴m+n=7,
答案为:7.
23.解:若△ABC是锐角三角形,则有a2+b2>c2(1分)
若△ABC是钝角三角形,∠C为钝角,则有a2+b2<c2.(2分)
当△ABC是锐角三角形时,
证明:过点A作AD⊥BC,垂足为D,设CD为x,则有BD=a﹣x(3分)
根据勾股定理,得b2﹣x2=AD2=c2﹣(a﹣x)2
即b2﹣x2=c2﹣a2+2ax﹣x2.
∴a2+b2=c2+2ax(5分)
∵a>0,x>0,
∴2ax>0.
∴a2+b2>c2.(6分)
当△ABC是钝角三角形时,
证明:过B作BD⊥AC,交AC的延长线于D.
设CD为y,则有BD2=a2﹣y2(7分)
根据勾股定理,得(b+y)2+a2﹣y2=c2.
即a2+b2+2by=c2.(9分)
∵b>0,y>0,
∴2by>0,
∴a2+b2<c2.(10分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
