浙江省宁波市艺术实验学校 2024 学年第二学期初二数学起始考(含答案)
文档属性
| 名称 | 浙江省宁波市艺术实验学校 2024 学年第二学期初二数学起始考(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 253.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-09 11:23:24 | ||
图片预览


文档简介
艺术实验 2024 学年第二学期初二数学自我评估卷 (2025.2)
一. 单项选择题 (每题 3 分, 共 30 分)
1.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
斐波那契螺旋线 B. 笛卡尔心形线 C.赵爽弦图 D. 科克曲线
2.下列二次根式中属于最简二次根式的是 ( )
A. B. C. D.
3.下列计算正确的是 ( )
A. B. C. D.
4.用反证法证明“已知: 中, ,求证: .”时,第一步应假设( )
A. B. C. D.
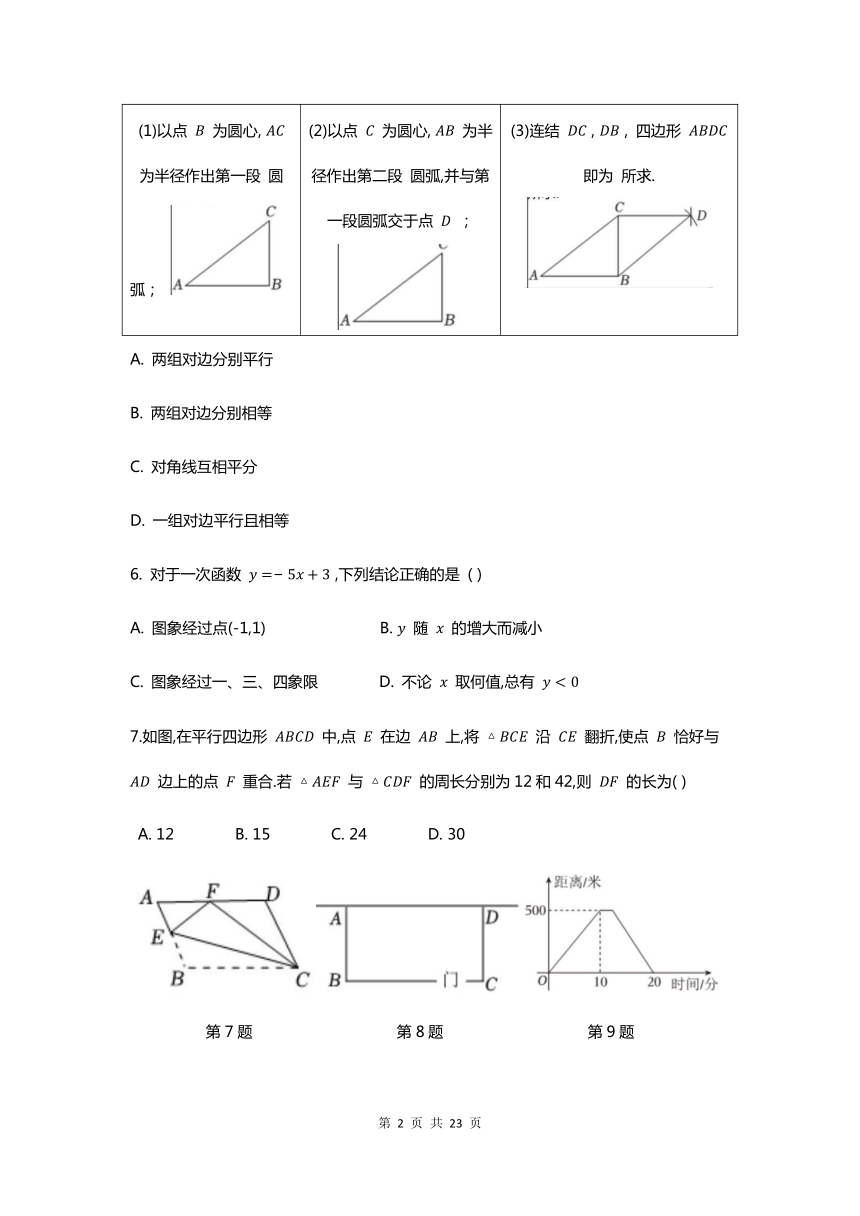
5.在综合实践课上,小明画出 , 利用尺规作图找一点 , 使得四边形 为平行四边形.如图是其作图过程.小明这一作法判定四边形 为平行四边形的直接依据是( )
(1)以点 为圆心, 为半径作出第一段 圆弧; (2)以点 为圆心, 为半径作出第二段 圆弧,并与第一段圆弧交于点 ; (3)连结 , , 四边形 即为 所求.
A. 两组对边分别平行
B. 两组对边分别相等
C. 对角线互相平分
D. 一组对边平行且相等
6. 对于一次函数 ,下列结论正确的是 ( )
A. 图象经过点(-1,1) B. 随 的增大而减小
C. 图象经过一、三、四象限 D. 不论 取何值,总有
7.如图,在平行四边形 中,点 在边 上,将 沿 翻折,使点 恰好与 边上的点 重合.若 与 的周长分别为12和42,则 的长为( )
A. 12 B. 15 C. 24 D. 30
第7题 第8题 第9题
8.如图,面积为 的矩形试验田一面靠墙(墙的长度不限),另外三面用 长的篱笆围成,平行于墙的一边开有一扇 宽的门 ( 门的材料另计)。设试验田垂直于墙的一边 的长为 ,则所列方程正确的是( )
A.
B.
C.
D.
9.小明和他家长晚餐后散步,去了离家500米的报亭,稍作停留后返回,如图是他们散步过程中离家的距离随时间变500化的情况,下面可能的情节是( )
A. 他们匀速步行去报亭,回家时加快了速度,匀速步行回家
B. 他们匀速步行去报亭,回家时减慢了速度,匀速步行回家
C. 他们去报亭时速度越来越快,回家时平均速度更快,但步行速度越来越慢
D. 他们去报亭时速度越来越快,回家时平均速度更慢,步行速度也越来越慢
10.如图,点 、 分别是平行四边形 边 、 上一点,连接 、 ,连接 交 于点 ,连接 分别交 、 于点 、 ,设 的面积为 , 的面积为 ,四边形 的面积为 ,若 , , ,则阴影部分四边形AGHP的面积为( )
A. 17 B. 19 C. 18 D. 25
二. 填空题 (每题 3 分, 共 18 分)
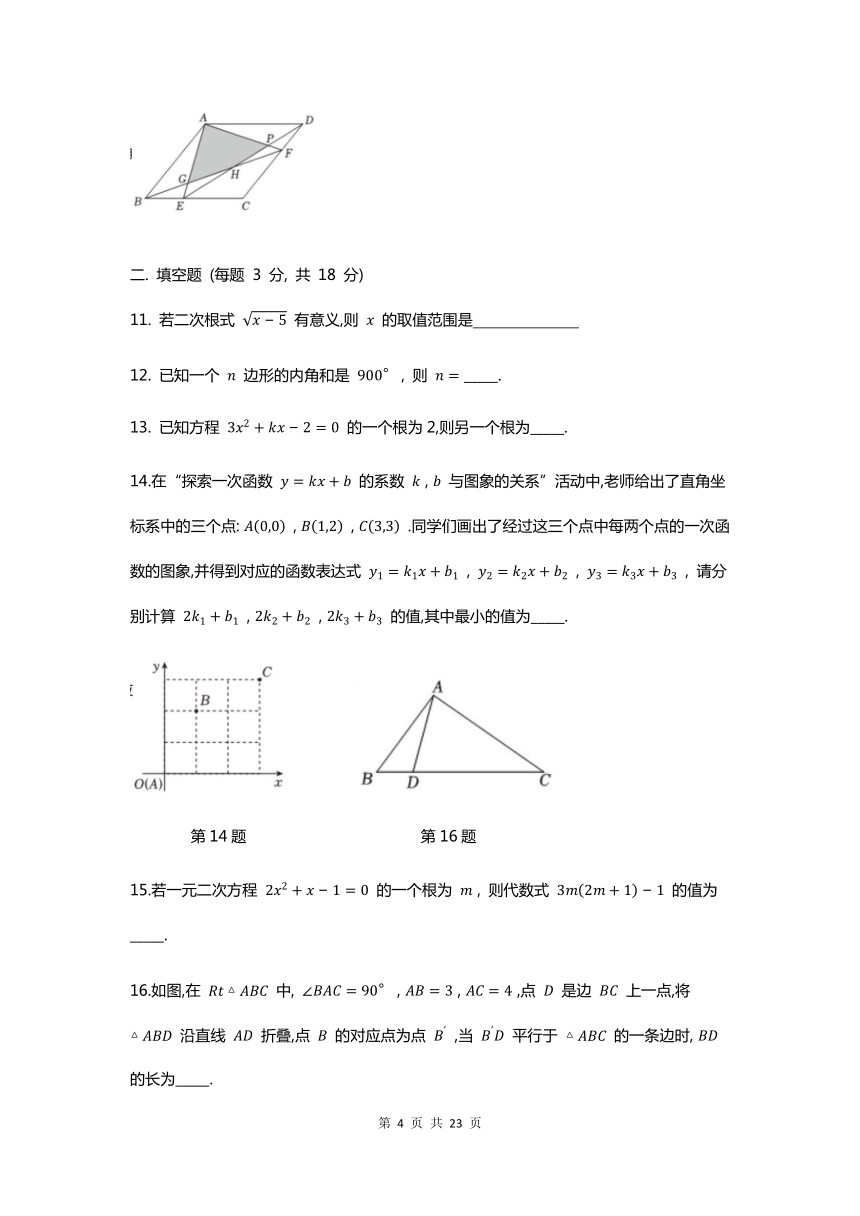
若二次根式 有意义,则 的取值范围是
已知一个 边形的内角和是 , 则 _____.
已知方程 的一个根为2,则另一个根为_____.
14.在“探索一次函数 的系数 , 与图象的关系”活动中,老师给出了直角坐标系中的三个点: , , .同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式 , , , 请分别计算 , , 的值,其中最小的值为_____.
第14题 第16题
15.若一元二次方程 的一个根为 , 则代数式 的值为_____.
16.如图,在 中, , , ,点 是边 上一点,将 沿直线 折叠,点 的对应点为点 ,当 平行于 的一条边时, 的长为_____.
三. 解答题 (共 8 小题, 共 52 分)
17. (4 分) 计算:
(1) ; (2) .
18. (4 分) 解方程:
(1) ; (2) ;
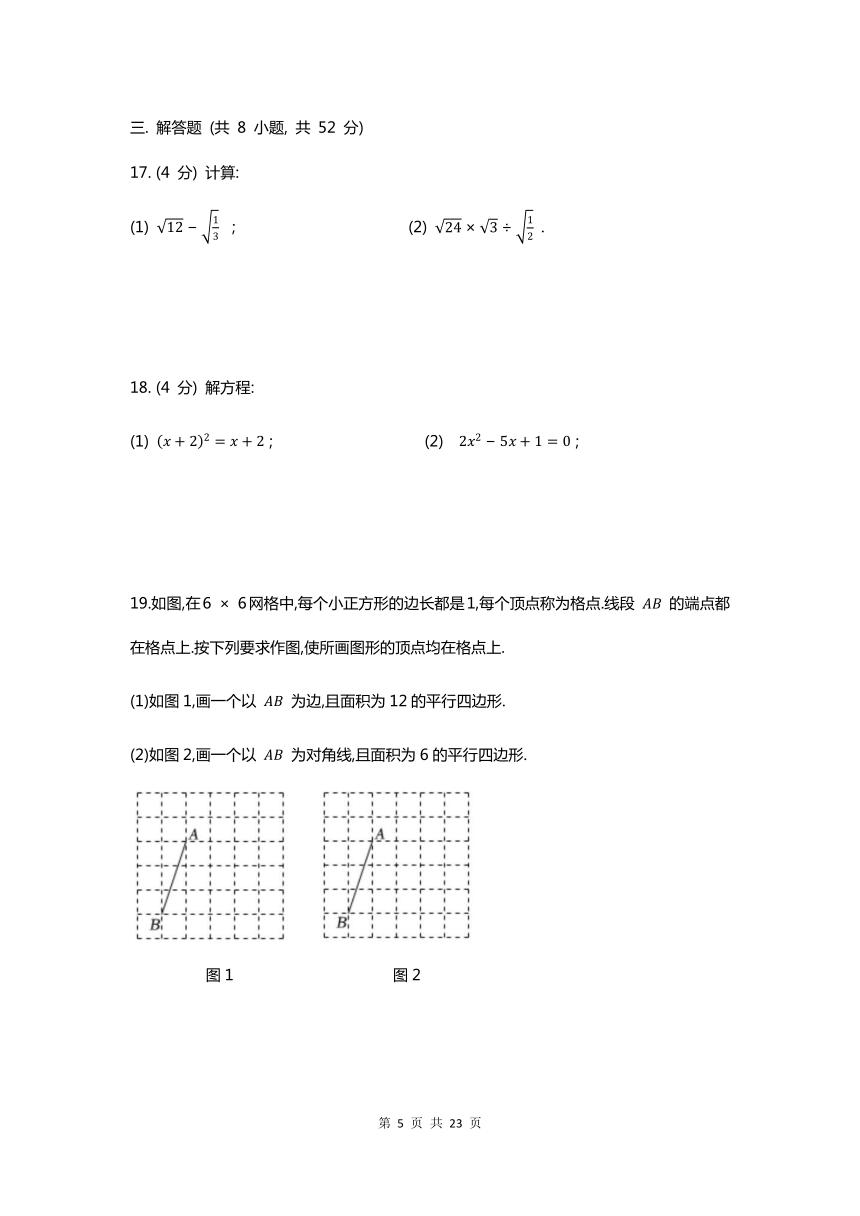
19.如图,在6 6网格中,每个小正方形的边长都是1,每个顶点称为格点.线段 的端点都在格点上.按下列要求作图,使所画图形的顶点均在格点上.
(1)如图1,画一个以 为边,且面积为12的平行四边形.
(2)如图2,画一个以 为对角线,且面积为6的平行四边形.
图1 图2
20.如图,四边形 为平行四边形,线段 为对角线,点 、 分别为线段 、 的中点,连接 交 于点 .
(1)求证:四边形 为平行四边形;
(2)若 ,求 的长.
21.某汽车租赁公司共有300辆可供出租的某款汽车,2021年每辆汽车的日租金为100元,由于物价上涨,到2023年日租金上涨到 121元.
(1)求2021年至2023年日租金的平均增长率;
(2)经市场调研发现,从2023年开始,当每辆汽车的日租金定为121元时,汽车可全部租出;日租金每增加1元,就要少租出2
辆. 已知汽车租赁公司每日需为每辆租出的汽车支付各类费用31元,每辆未租出的汽车支付各类费用10元.
①在每辆汽车日租金121元的基础上,设上涨 元,则每辆汽车的日租金为_____元,实际能租出_____辆车.
②当每辆汽车的日租金上涨多少元时,该租赁公司的日收益可达28200元?(日收益=总租金-各类费用)
22.如图,直线 过点 , .
(1) 求直线 的解析式.
(2)若直线 与直线 相交于点 , 求点 的坐标.
(3)根据图象,写出关于 的不等式 的解集.
23.综合与实践
【情境描述】
圆圆想把一些相同规格的塑料杯,尽可能多地放入高40 的柜子里(如图1).她把杯子按如图这样整齐地叠放成一摞 (如图2),但她不知道一摞最多能叠几个可以一次性放进柜子里.
【观察发现】
圆圆测量后发现,按这样叠放,这摞杯子的总高度随着杯子数量的变化而变化,记录的数据如下表所示:
杯子的数量 (只) 1 2 3 4 5 6 ...
总高度 10 11.4 12.8 14.2 15.6 17 ...
【建立模型】
(1)请根据上表中的信息,在平面直角坐标系中描出对应点,观察这些点的分布规律,试求 关于 的函数表达式.
( 2 )当杯子的数量为12只时,求这摞杯子的总高度.
【解决问题】
请帮圆圆算一算,一摞最多能叠几个杯子,可以一次性放进柜子里? A
图 1 图 2
24.如图,在四边形 中, , , ,动点 、 分别从 、 同时出发,点 以 的速度由 向 运动,点 以 的速度由 向 运动,其中一动点到达终点时,另一动点随之停止运动,设运动时间为 秒.
分别用含有 的式子表示);
(2)当四边形 的面积是四边形 面积的2倍时,求出 的值.
(3)当点 、 与四边形 的任意两个顶点所形成的四边形是平行四边形时,直接写出 的值.
四、附加题 (3+3+4, 共 10 分):
25. 如果直角三角形的三边都是 200 以内的正整数, 且较长的两边长相差 1 , 那么这样直角三角形有_____个.
26. 若不等式 对任意正整数 都成立,且 是正整数,求 的最小值为_____.
27. 已知正实数 满足 ,则 的最小值为_____.
参考答案
1.【答案】
不是轴对称图形,也不是中心对称图形,故此选项不合题意;
是轴对称图形,不是中心对称图形,故此选项不合题意;
不是轴对称图形,是中心对称图形,故此选项不合题意;
.既是轴对称图形又是中心对称图形,故此选项符合题意;
故选: .
2.【答案】
、 是最简二次根式,符合题意; ,被开方数中含能开得尽方的因式,不是最简二次根式,不符合题意;
、,被开方数中含能开得尽方的因式,不是最简二次根式,不符合题意;
、被开方数含分母,不是最简二次根式,不符合题意;
、 ,被开方数中含能开得尽方的因式,不是最简二次根式,不符合题意;
故选: A .
3【答案】
,因此选项 不符合题意;
,因此选项 不符合题意;
,因此选项 符合题意;
, 因此选项 不符合题意.
故选: .
4.【答案】
用反证法证明:“已知在 中, ,求证 .”时,
第一步应假设 ,
故选: .
5.【答案】
由作图过程可得, , ,
四边形 为平行四边形,
即判定依据为两组对边分别相等.
故选: .
6.【答案】
故选:
7.【答案】
与 的周长分别为12和42,
, ,
四边形 是平行四边形,
,
将 沿 翻折,点 与 边上的点 重合,
,
,
,
,
,
,
故选: .
8.【答案】
篱笆的总长为 , 且 , 平行于墙的一边开有一扇1 宽的门,
.
依题意得 .
故选: .
9.【答案】
他们匀速步行去报亭的数据为10分钟,在报亭停留了一会,然后回家,一共用了20分钟,
他们回家用的数据少于去报亭的数据,
说明他们他们匀速步行去报亭,回家时加快了速度,匀速步行回家,
故选: .
10.【答案】
四边形 是平行四边形,
,
设 与 之间的距离为 , 与 之间的距离为 ,
,
,
,
,
,
,
故选: .
11【答案】
根据二次根式的性质,被开方数大于或等于 0,可以求出 的范围.
根据题意得 ,
解得 .
故答案为: .
12【答案】
这个多边形的边数是 ,
则: ,
解得 .
故答案为:7 .
13【答案】
令方程的另一个根为 ,
则 ,
所以 ,
即方程的另一个根为 .
故答案为: .
14【答案】
不妨设直线 的函数表达式为 ,直线 的函数表达式为 ,直线 的函数表达式
点 的坐标为(0,0),点 的坐标为(1,2),点 的坐标为(3,3),
解得 ,
, , .
又 ,
其中最小的值为 2 .
故答案为:2 .
15【答案】
由题意得:把 代入方程 中得: ,
,
,
故答案为 : 2 .
16【答案】
如图1, , 设 交 于点 , 则
, , ,
图1
, ,
由折叠得 ,
, , ,
,
,
, ,
,
解得 ,
, ,
,
,
,
解得 ;
如图2, , 则 ,
图2
由折叠得 ,
,
;
点 在 上,
不存在 的情况,
综上所述, 的长为1或3,
故答案为 : 1 或 3 .
17【答案】
( 1 ) 原式
;
(2)原式
.
18【答案】
(1) ,
,
解得 .
(2) ,
,
方程有两个不相等的实数根,
,
解得 .
19【答案】
(1)如图1所示,平行四边形 即为所求(答案不唯一)。
图1 图2
(2)如图2所示,四边形 即为所求.
20【答案】
(1)证明: 四边形 为平行四边形,
,
点 、 分别为线段 、 的中点,
,
,
,
四边形 为平行四边形;
四边形 为平行四边形,
,
,
为 的中位线,
.
21【答案】
(1)设2021年至2023年日租金的平均增长率为 ,
根据题意得 ,
解得: , (不符合题意,舍去)。
答:2021年至2023年日租金的平均增长率为10%;
根据题意得:在每辆汽车日租金121元的基础上,设上涨 元,则每辆汽车的日租金为 元,
实际能租出(300 - 2y)辆.
故答案为: ,(300 - 2y);
②根据题意得: ,
整理得 ,
解得 , .
答:当每辆汽车的日租金上涨20或30元时,该租赁公司的日收益可达28200元.
22【答案】
直线 过点 , .
解方程组得 ,
直线 的解析式为 ;
直线 与直线 相交于点 ,
解方程组 ,
解得 ,
点 的坐标为(3,2);
23【答案】 [建立模型] (1)描点,连线, 根据点的分布规律可知, 关于 的函数关系式满足一次函数,
设 关于 的函数关系式为 ,
则 ,
解得 ,
关于 的函数关系式为 ;
(2)当 时, ,
这摞杯子的总高度 ;
[解决问题]
当 时, ,
解得 ,
一摞最多能叠22个杯子,可以一次性放进柜子里.
24【答案】
点 以 的速度由 向 运动,点 以 的速度由 向 运动,
, ,
,
故答案为: , ;
(2) 设点 到 的距离为 ,
四边形 的面积是四边形 面积的2倍,
,
;
(3)若四边形 是平行四边形,
,
,
;
若四边形 是平行四边形,
,
,
,
若四边形 是平行四边形,
,
,
(不合题意舍去) ,
若四边形 是平行四边形,
,
,
,
综上所述:当 或3或 时,点 、 与四边形 的任意两个顶点所形成的四边形是平行四边形.
附加题
1【答案】
不妨设该直角三角形的是三边长依次为 , , , 其中 , 、 ,
由勾股定理知 ,
显然 为大于1且小于401的奇数,所以 为大于1且小于20的奇数,
则 ,5,7,9,11,13,15,17,19, 即满足题意的直角三角形有9个.
故答案为 : 9 .
2【答案】
根据题意,设 , ,
,
的值随 的增大而减少,
当 时, 有最大值, ,
,
,
的最小值是 2023.
3【答案】
过 作直线与 平行,过 作与 平行的直线交于
且
的最小值为 18
一. 单项选择题 (每题 3 分, 共 30 分)
1.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
斐波那契螺旋线 B. 笛卡尔心形线 C.赵爽弦图 D. 科克曲线
2.下列二次根式中属于最简二次根式的是 ( )
A. B. C. D.
3.下列计算正确的是 ( )
A. B. C. D.
4.用反证法证明“已知: 中, ,求证: .”时,第一步应假设( )
A. B. C. D.
5.在综合实践课上,小明画出 , 利用尺规作图找一点 , 使得四边形 为平行四边形.如图是其作图过程.小明这一作法判定四边形 为平行四边形的直接依据是( )
(1)以点 为圆心, 为半径作出第一段 圆弧; (2)以点 为圆心, 为半径作出第二段 圆弧,并与第一段圆弧交于点 ; (3)连结 , , 四边形 即为 所求.
A. 两组对边分别平行
B. 两组对边分别相等
C. 对角线互相平分
D. 一组对边平行且相等
6. 对于一次函数 ,下列结论正确的是 ( )
A. 图象经过点(-1,1) B. 随 的增大而减小
C. 图象经过一、三、四象限 D. 不论 取何值,总有
7.如图,在平行四边形 中,点 在边 上,将 沿 翻折,使点 恰好与 边上的点 重合.若 与 的周长分别为12和42,则 的长为( )
A. 12 B. 15 C. 24 D. 30
第7题 第8题 第9题
8.如图,面积为 的矩形试验田一面靠墙(墙的长度不限),另外三面用 长的篱笆围成,平行于墙的一边开有一扇 宽的门 ( 门的材料另计)。设试验田垂直于墙的一边 的长为 ,则所列方程正确的是( )
A.
B.
C.
D.
9.小明和他家长晚餐后散步,去了离家500米的报亭,稍作停留后返回,如图是他们散步过程中离家的距离随时间变500化的情况,下面可能的情节是( )
A. 他们匀速步行去报亭,回家时加快了速度,匀速步行回家
B. 他们匀速步行去报亭,回家时减慢了速度,匀速步行回家
C. 他们去报亭时速度越来越快,回家时平均速度更快,但步行速度越来越慢
D. 他们去报亭时速度越来越快,回家时平均速度更慢,步行速度也越来越慢
10.如图,点 、 分别是平行四边形 边 、 上一点,连接 、 ,连接 交 于点 ,连接 分别交 、 于点 、 ,设 的面积为 , 的面积为 ,四边形 的面积为 ,若 , , ,则阴影部分四边形AGHP的面积为( )
A. 17 B. 19 C. 18 D. 25
二. 填空题 (每题 3 分, 共 18 分)
若二次根式 有意义,则 的取值范围是
已知一个 边形的内角和是 , 则 _____.
已知方程 的一个根为2,则另一个根为_____.
14.在“探索一次函数 的系数 , 与图象的关系”活动中,老师给出了直角坐标系中的三个点: , , .同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式 , , , 请分别计算 , , 的值,其中最小的值为_____.
第14题 第16题
15.若一元二次方程 的一个根为 , 则代数式 的值为_____.
16.如图,在 中, , , ,点 是边 上一点,将 沿直线 折叠,点 的对应点为点 ,当 平行于 的一条边时, 的长为_____.
三. 解答题 (共 8 小题, 共 52 分)
17. (4 分) 计算:
(1) ; (2) .
18. (4 分) 解方程:
(1) ; (2) ;
19.如图,在6 6网格中,每个小正方形的边长都是1,每个顶点称为格点.线段 的端点都在格点上.按下列要求作图,使所画图形的顶点均在格点上.
(1)如图1,画一个以 为边,且面积为12的平行四边形.
(2)如图2,画一个以 为对角线,且面积为6的平行四边形.
图1 图2
20.如图,四边形 为平行四边形,线段 为对角线,点 、 分别为线段 、 的中点,连接 交 于点 .
(1)求证:四边形 为平行四边形;
(2)若 ,求 的长.
21.某汽车租赁公司共有300辆可供出租的某款汽车,2021年每辆汽车的日租金为100元,由于物价上涨,到2023年日租金上涨到 121元.
(1)求2021年至2023年日租金的平均增长率;
(2)经市场调研发现,从2023年开始,当每辆汽车的日租金定为121元时,汽车可全部租出;日租金每增加1元,就要少租出2
辆. 已知汽车租赁公司每日需为每辆租出的汽车支付各类费用31元,每辆未租出的汽车支付各类费用10元.
①在每辆汽车日租金121元的基础上,设上涨 元,则每辆汽车的日租金为_____元,实际能租出_____辆车.
②当每辆汽车的日租金上涨多少元时,该租赁公司的日收益可达28200元?(日收益=总租金-各类费用)
22.如图,直线 过点 , .
(1) 求直线 的解析式.
(2)若直线 与直线 相交于点 , 求点 的坐标.
(3)根据图象,写出关于 的不等式 的解集.
23.综合与实践
【情境描述】
圆圆想把一些相同规格的塑料杯,尽可能多地放入高40 的柜子里(如图1).她把杯子按如图这样整齐地叠放成一摞 (如图2),但她不知道一摞最多能叠几个可以一次性放进柜子里.
【观察发现】
圆圆测量后发现,按这样叠放,这摞杯子的总高度随着杯子数量的变化而变化,记录的数据如下表所示:
杯子的数量 (只) 1 2 3 4 5 6 ...
总高度 10 11.4 12.8 14.2 15.6 17 ...
【建立模型】
(1)请根据上表中的信息,在平面直角坐标系中描出对应点,观察这些点的分布规律,试求 关于 的函数表达式.
( 2 )当杯子的数量为12只时,求这摞杯子的总高度.
【解决问题】
请帮圆圆算一算,一摞最多能叠几个杯子,可以一次性放进柜子里? A
图 1 图 2
24.如图,在四边形 中, , , ,动点 、 分别从 、 同时出发,点 以 的速度由 向 运动,点 以 的速度由 向 运动,其中一动点到达终点时,另一动点随之停止运动,设运动时间为 秒.
分别用含有 的式子表示);
(2)当四边形 的面积是四边形 面积的2倍时,求出 的值.
(3)当点 、 与四边形 的任意两个顶点所形成的四边形是平行四边形时,直接写出 的值.
四、附加题 (3+3+4, 共 10 分):
25. 如果直角三角形的三边都是 200 以内的正整数, 且较长的两边长相差 1 , 那么这样直角三角形有_____个.
26. 若不等式 对任意正整数 都成立,且 是正整数,求 的最小值为_____.
27. 已知正实数 满足 ,则 的最小值为_____.
参考答案
1.【答案】
不是轴对称图形,也不是中心对称图形,故此选项不合题意;
是轴对称图形,不是中心对称图形,故此选项不合题意;
不是轴对称图形,是中心对称图形,故此选项不合题意;
.既是轴对称图形又是中心对称图形,故此选项符合题意;
故选: .
2.【答案】
、 是最简二次根式,符合题意; ,被开方数中含能开得尽方的因式,不是最简二次根式,不符合题意;
、,被开方数中含能开得尽方的因式,不是最简二次根式,不符合题意;
、被开方数含分母,不是最简二次根式,不符合题意;
、 ,被开方数中含能开得尽方的因式,不是最简二次根式,不符合题意;
故选: A .
3【答案】
,因此选项 不符合题意;
,因此选项 不符合题意;
,因此选项 符合题意;
, 因此选项 不符合题意.
故选: .
4.【答案】
用反证法证明:“已知在 中, ,求证 .”时,
第一步应假设 ,
故选: .
5.【答案】
由作图过程可得, , ,
四边形 为平行四边形,
即判定依据为两组对边分别相等.
故选: .
6.【答案】
故选:
7.【答案】
与 的周长分别为12和42,
, ,
四边形 是平行四边形,
,
将 沿 翻折,点 与 边上的点 重合,
,
,
,
,
,
,
故选: .
8.【答案】
篱笆的总长为 , 且 , 平行于墙的一边开有一扇1 宽的门,
.
依题意得 .
故选: .
9.【答案】
他们匀速步行去报亭的数据为10分钟,在报亭停留了一会,然后回家,一共用了20分钟,
他们回家用的数据少于去报亭的数据,
说明他们他们匀速步行去报亭,回家时加快了速度,匀速步行回家,
故选: .
10.【答案】
四边形 是平行四边形,
,
设 与 之间的距离为 , 与 之间的距离为 ,
,
,
,
,
,
,
故选: .
11【答案】
根据二次根式的性质,被开方数大于或等于 0,可以求出 的范围.
根据题意得 ,
解得 .
故答案为: .
12【答案】
这个多边形的边数是 ,
则: ,
解得 .
故答案为:7 .
13【答案】
令方程的另一个根为 ,
则 ,
所以 ,
即方程的另一个根为 .
故答案为: .
14【答案】
不妨设直线 的函数表达式为 ,直线 的函数表达式为 ,直线 的函数表达式
点 的坐标为(0,0),点 的坐标为(1,2),点 的坐标为(3,3),
解得 ,
, , .
又 ,
其中最小的值为 2 .
故答案为:2 .
15【答案】
由题意得:把 代入方程 中得: ,
,
,
故答案为 : 2 .
16【答案】
如图1, , 设 交 于点 , 则
, , ,
图1
, ,
由折叠得 ,
, , ,
,
,
, ,
,
解得 ,
, ,
,
,
,
解得 ;
如图2, , 则 ,
图2
由折叠得 ,
,
;
点 在 上,
不存在 的情况,
综上所述, 的长为1或3,
故答案为 : 1 或 3 .
17【答案】
( 1 ) 原式
;
(2)原式
.
18【答案】
(1) ,
,
解得 .
(2) ,
,
方程有两个不相等的实数根,
,
解得 .
19【答案】
(1)如图1所示,平行四边形 即为所求(答案不唯一)。
图1 图2
(2)如图2所示,四边形 即为所求.
20【答案】
(1)证明: 四边形 为平行四边形,
,
点 、 分别为线段 、 的中点,
,
,
,
四边形 为平行四边形;
四边形 为平行四边形,
,
,
为 的中位线,
.
21【答案】
(1)设2021年至2023年日租金的平均增长率为 ,
根据题意得 ,
解得: , (不符合题意,舍去)。
答:2021年至2023年日租金的平均增长率为10%;
根据题意得:在每辆汽车日租金121元的基础上,设上涨 元,则每辆汽车的日租金为 元,
实际能租出(300 - 2y)辆.
故答案为: ,(300 - 2y);
②根据题意得: ,
整理得 ,
解得 , .
答:当每辆汽车的日租金上涨20或30元时,该租赁公司的日收益可达28200元.
22【答案】
直线 过点 , .
解方程组得 ,
直线 的解析式为 ;
直线 与直线 相交于点 ,
解方程组 ,
解得 ,
点 的坐标为(3,2);
23【答案】 [建立模型] (1)描点,连线, 根据点的分布规律可知, 关于 的函数关系式满足一次函数,
设 关于 的函数关系式为 ,
则 ,
解得 ,
关于 的函数关系式为 ;
(2)当 时, ,
这摞杯子的总高度 ;
[解决问题]
当 时, ,
解得 ,
一摞最多能叠22个杯子,可以一次性放进柜子里.
24【答案】
点 以 的速度由 向 运动,点 以 的速度由 向 运动,
, ,
,
故答案为: , ;
(2) 设点 到 的距离为 ,
四边形 的面积是四边形 面积的2倍,
,
;
(3)若四边形 是平行四边形,
,
,
;
若四边形 是平行四边形,
,
,
,
若四边形 是平行四边形,
,
,
(不合题意舍去) ,
若四边形 是平行四边形,
,
,
,
综上所述:当 或3或 时,点 、 与四边形 的任意两个顶点所形成的四边形是平行四边形.
附加题
1【答案】
不妨设该直角三角形的是三边长依次为 , , , 其中 , 、 ,
由勾股定理知 ,
显然 为大于1且小于401的奇数,所以 为大于1且小于20的奇数,
则 ,5,7,9,11,13,15,17,19, 即满足题意的直角三角形有9个.
故答案为 : 9 .
2【答案】
根据题意,设 , ,
,
的值随 的增大而减少,
当 时, 有最大值, ,
,
,
的最小值是 2023.
3【答案】
过 作直线与 平行,过 作与 平行的直线交于
且
的最小值为 18
同课章节目录
