华师大版七下(2024版)7.3解一元一次不等式第1课时学案
文档属性
| 名称 | 华师大版七下(2024版)7.3解一元一次不等式第1课时学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第7章 一元一次不等式
7.3 解一元一次不等式第一课时
学习目标与重难点
学习目标:
1.理解一元一次不等式的概念.
2.掌握解不等式的步骤,体会数学运算中类比和转化的方法运用.
3.学会用数轴表示解集,加深对数形结合思想的进一步理解和掌握.
学习重点:通过类比一元一次方程的解法,掌握一元一次不等式的解法.
学习难点:会在数轴上表示一元一次不等式的解集.
预习自测
一、知识链接
1、什么叫一元一次方程?
解一元一次方程的步骤是什么?
自学自测
1.下列不等式是一元一次不等式的是( )
A.2x(x-3)>8 B.x+2y<1
C.2x-3>5 D.-2>8
2.不等式x-2<0的解集是( )
A.x<2 B.x>2
C.x<-2 D.x>-2
3.不等式3x≥x-4的解集是( )
A.x≥-2 B.x≤-2
C.x>-2 D.x<-2
教学过程
一、创设情境、导入新课
1.什么叫一元一次方程
不等式的基本性质:
3.解一元一次方程的一般步骤是什么?
二、合作交流、新知探究
探究一:一元一次不等式的定义
教材第64页
在前面我们遇到过一些含有未知数的不等式,
例如
,, 等
思考:它们有哪些共同特征?
【互动】(小组讨论)根据一元一次方程的概念,你们能归纳出一元一次不等式的概念吗?
[概念总结]像这样,只含有一个未知数、左右两边都是整式,并且未知数的次数都是1的不等式,叫做一元一次不等式(linear inequality with one unknown) .
做一做:
下列不等式中,哪些是一元一次不等式
(1); (2);
(3); (4).
【强调】:
探究二:解一元一次不等式
教材第64页:例题讲解
与解方程类似, 解不等式的过程, 就是利用不等式的基本性质, 将不等式进行适当的变形, 得到 或 的形式.
[典型例题]例1 解不等式:
(1); (2).
思考:这两道小题中不等式的变形与方程的什么变形类似
【强调】:不等式一边的某一项变号后移到另一边,我们把这种变形称为移项.
[典型例题]例2 解不等式:利用不等式的基本性质说明下列结论的正确性:
(1);(2).
思考:这两小题中不等式的变形与方程的什么变形类似 有什么不同
注意:
不等式的两边都乘以(或都除以)的数是正数时,不等号的方向不变;
不等式的两边都乘以(或都除以)的数是负数时,不等号的方向改变.
[典型例题]例3 解下列不等式,并将解集在数轴上表示出来:
(1);
(2).
思考:解一元一次不等式与解一元一次方程的依据和步骤有什么异同点?
[典型例题]例4 当取何值时,代数式与的差大于1?
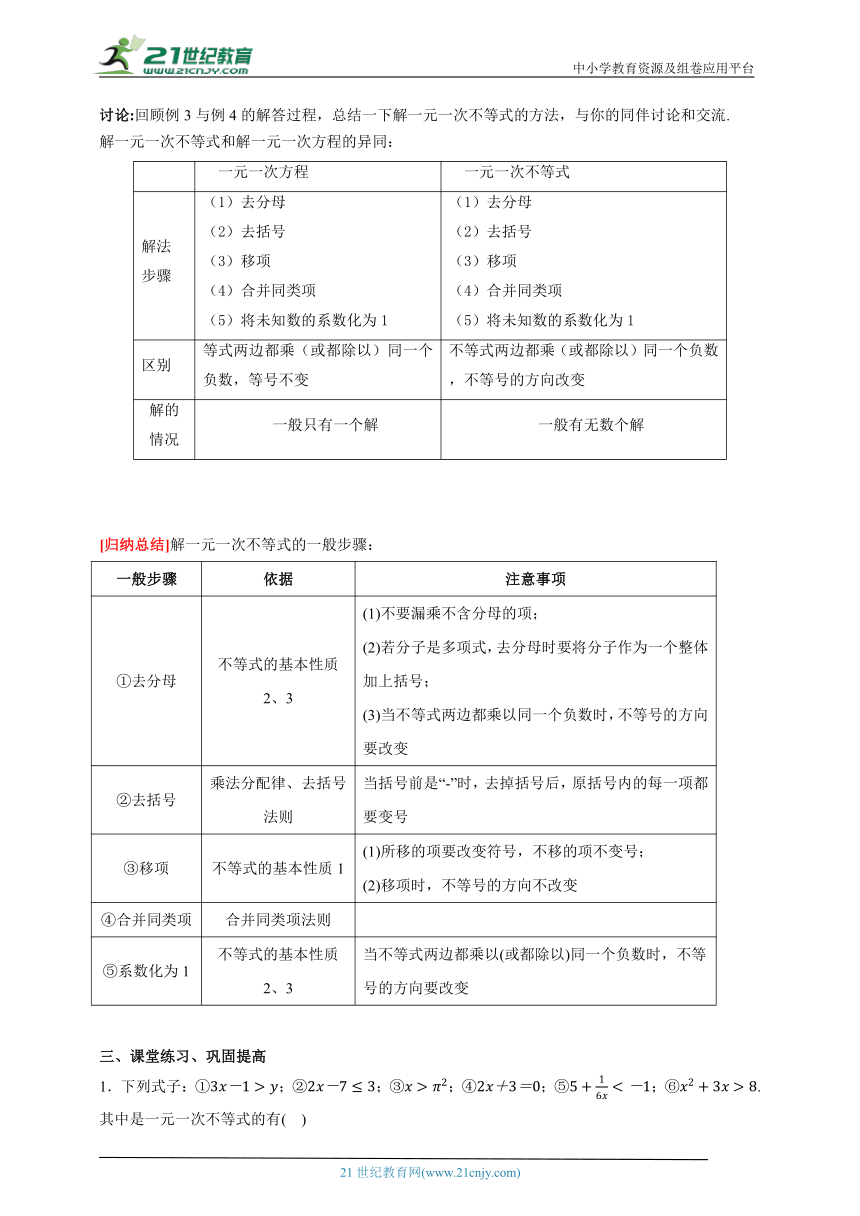
讨论:回顾例3与例4的解答过程,总结一下解一元一次不等式的方法,与你的同伴讨论和交流.
解一元一次不等式和解一元一次方程的异同:
一元一次方程 一元一次不等式
解法 步骤 (1)去分母 (2)去括号 (3)移项 (4)合并同类项 (5)将未知数的系数化为1 (1)去分母 (2)去括号 (3)移项 (4)合并同类项 (5)将未知数的系数化为1
区别 等式两边都乘(或都除以)同一个负数,等号不变 不等式两边都乘(或都除以)同一个负数,不等号的方向改变
解的 情况 一般只有一个解 一般有无数个解
[归纳总结]解一元一次不等式的一般步骤:
一般步骤 依据 注意事项
①去分母 不等式的基本性质2、3 (1)不要漏乘不含分母的项; (2)若分子是多项式,去分母时要将分子作为一个整体加上括号; (3)当不等式两边都乘以同一个负数时,不等号的方向要改变
②去括号 乘法分配律、去括号法则 当括号前是“-”时,去掉括号后,原括号内的每一项都要变号
③移项 不等式的基本性质1 (1)所移的项要改变符号,不移的项不变号; (2)移项时,不等号的方向不改变
④合并同类项 合并同类项法则
⑤系数化为1 不等式的基本性质2、3 当不等式两边都乘以(或都除以)同一个负数时,不等号的方向要改变
三、课堂练习、巩固提高
1.下列式子:①;②;③;④;⑤;⑥.其中是一元一次不等式的有( )
A.1个 B.2个 C.3个 D.4个
2.不等式的解集是( )
A. B. C. D.
3.下列数中,能使不等式成立的的值为( )
A.1 B.2 C.3 D.4
4.若是关于x的一元一次不等式,则m=________.
选做题:
5.不等式的解集为________.
6.不等式的非负整数解有________个.
7.解不等式:
(1);(2);
【综合拓展类作业】
解不等式,并把解集在数轴上表示出来.
总结反思、拓展升华
【课堂总结】
知识点:
解一元一次不等式的一般步骤
(1)去分母——不等式性质2或3.
注意:①勿漏乘不含分母的项;②分子是两项或两项以上的代数式时要加括号;③若两边同时乘一个负数,要注意不等号的方向要改变.
(2)去括号——去括号法则和分配律.
注意:①勿漏乘括号内每一项;②括号前面是负号,括号内各项要变号.
(3)移项——移项法则(不等式的性质1).
注意:移项要变号.
(4)合并同类项——合并同类项法则.
(5)将未知数的系数化成1——不等式的性质2或3.
注意:两边同时除以未知数的系数时,要分清不等号的方向是否改变.
数学思想方法:
类比思想
五、【作业布置】
【知识技能类作业】
必做题:
1.下列不等式中不是一元一次不等式的是( )
A.2x>1 B.b<3 C.1-a≤a D.->1
2.已知|3-a|=a-3,则a的取值范围在数轴上表示正确的是( )
3.不等式3x-2>1的最小整数解是( )
A.0 B.1 C.2 D.3
4.若关于x的不等式mx-n>0的解集是x<,则关于x的不等式(m+n)x>n-m的解集是( )
A.x<- B.x>- C.x< D.x>
5.关于x的不等式m-≤1-x有正数解,m的值可以是________(写出一个即可).
选做题:
6.(1)解不等式:-1≤,把它的解集表示在数轴上;
(2)解不等式:<x+1,并把解集在数轴上表示出来.
已知关于x的不等式4x-3a>-1与2(x-1)+3>5的解集相同,求a的值.
8.已知整式的值为P.
(1)当m=1时,求P的值;
(2)若P的取值范围如图所示,求m的取值范围.
【综合拓展类作业】
9.关于x的不等式(2a-b)x>a-2b的解集是x<,求关于x的不等式ax+b<0的解集.
答案:
自学自测:
1.C 2.A 3.A
课堂练习:
1.B 2.D 3.A 4.2
5. 6.4
7.解:(1),
去括号,得.
移项,得.
合并同类项,得.
两边都除以2,得.
(2),
去分母,得,
去括号,得,
移项,得,
合并同类项,得,
两边都除以-5,得.
8.解:去分母,得.
去括号,得.
移项、合并同类项,得.
系数化为1,得.
这个不等式的解集在数轴上表示为:
作业布置:
1.D 解析:A.2x>1是一元一次不等式,不符合题意;B.b<3是一元一次不等式,不符合题意;C.1-a≤a是一元一次不等式,不符合题意;D.->1不是一元一次不等式,符合题意.故选D.
2.A 解析:∵|3-a|=a-3,
∴a-3≥0.∴a≥3.故选A.
3.C 解析:3x-2>1,解得x>1,x的最小整数解为2.故选C.
4.A 解析:∵关于x的不等式mx-n>0的解集是x<,∴m<0,=.∴m=5n.∴n<0.∴m+n<0.∴解关于x的不等式(m+n)x>n-m,得x<.∴x<=-.故选A.
5.0(答案不唯一) 解析:原不等式整理,得x≤1-m,
解得x≤2-2m.
∵原不等式有正数解,
∴2-2m>0.
解得m<1,
则m的值可以是0.(答案不唯一)
6.解:(1)-1≤,
去分母,得2(x+1)-6≤3(2-x).
去括号,得2x+2-6≤6-3x.
移项,得2x+3x≤6+6-2.
合并同类项,得5x≤10.
系数化为1,得x≤2.
其解集在数轴上表示如下:
(2)<x+1,
去分母,得x-1<2(x+1).
去括号,得x-1<2x+2.
移项,得x-2x<2+1.
合并同类项,得-x<3.
系数化为1,得x>-3.
其解集在数轴上表示如下:
7.解:由4x-3a>-1,得x>.
由2(x-1)+3>5,得x>2.
∵这两个不等式的解集相同,
∴=2,即3a-1=8.
∴a=3.
8.解:(1)当m=1时,
P=3=3×=4,
∴P的值是4.
(2)根据题意,得3≤7,
解得m≤2,
∴m的取值范围是m≤2.
9.解:由(2a-b)x>a-2b的解集是x<,可知2a-b<0,
即x<,所以=.所以b=8a.代入ax+b<0,得ax+8a<0.又因为2a-b<0,所以2a-8a<0.所以a>0.所以ax<-8a. 所以x<-8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第7章 一元一次不等式
7.3 解一元一次不等式第一课时
学习目标与重难点
学习目标:
1.理解一元一次不等式的概念.
2.掌握解不等式的步骤,体会数学运算中类比和转化的方法运用.
3.学会用数轴表示解集,加深对数形结合思想的进一步理解和掌握.
学习重点:通过类比一元一次方程的解法,掌握一元一次不等式的解法.
学习难点:会在数轴上表示一元一次不等式的解集.
预习自测
一、知识链接
1、什么叫一元一次方程?
解一元一次方程的步骤是什么?
自学自测
1.下列不等式是一元一次不等式的是( )
A.2x(x-3)>8 B.x+2y<1
C.2x-3>5 D.-2>8
2.不等式x-2<0的解集是( )
A.x<2 B.x>2
C.x<-2 D.x>-2
3.不等式3x≥x-4的解集是( )
A.x≥-2 B.x≤-2
C.x>-2 D.x<-2
教学过程
一、创设情境、导入新课
1.什么叫一元一次方程
不等式的基本性质:
3.解一元一次方程的一般步骤是什么?
二、合作交流、新知探究
探究一:一元一次不等式的定义
教材第64页
在前面我们遇到过一些含有未知数的不等式,
例如
,, 等
思考:它们有哪些共同特征?
【互动】(小组讨论)根据一元一次方程的概念,你们能归纳出一元一次不等式的概念吗?
[概念总结]像这样,只含有一个未知数、左右两边都是整式,并且未知数的次数都是1的不等式,叫做一元一次不等式(linear inequality with one unknown) .
做一做:
下列不等式中,哪些是一元一次不等式
(1); (2);
(3); (4).
【强调】:
探究二:解一元一次不等式
教材第64页:例题讲解
与解方程类似, 解不等式的过程, 就是利用不等式的基本性质, 将不等式进行适当的变形, 得到 或 的形式.
[典型例题]例1 解不等式:
(1); (2).
思考:这两道小题中不等式的变形与方程的什么变形类似
【强调】:不等式一边的某一项变号后移到另一边,我们把这种变形称为移项.
[典型例题]例2 解不等式:利用不等式的基本性质说明下列结论的正确性:
(1);(2).
思考:这两小题中不等式的变形与方程的什么变形类似 有什么不同
注意:
不等式的两边都乘以(或都除以)的数是正数时,不等号的方向不变;
不等式的两边都乘以(或都除以)的数是负数时,不等号的方向改变.
[典型例题]例3 解下列不等式,并将解集在数轴上表示出来:
(1);
(2).
思考:解一元一次不等式与解一元一次方程的依据和步骤有什么异同点?
[典型例题]例4 当取何值时,代数式与的差大于1?
讨论:回顾例3与例4的解答过程,总结一下解一元一次不等式的方法,与你的同伴讨论和交流.
解一元一次不等式和解一元一次方程的异同:
一元一次方程 一元一次不等式
解法 步骤 (1)去分母 (2)去括号 (3)移项 (4)合并同类项 (5)将未知数的系数化为1 (1)去分母 (2)去括号 (3)移项 (4)合并同类项 (5)将未知数的系数化为1
区别 等式两边都乘(或都除以)同一个负数,等号不变 不等式两边都乘(或都除以)同一个负数,不等号的方向改变
解的 情况 一般只有一个解 一般有无数个解
[归纳总结]解一元一次不等式的一般步骤:
一般步骤 依据 注意事项
①去分母 不等式的基本性质2、3 (1)不要漏乘不含分母的项; (2)若分子是多项式,去分母时要将分子作为一个整体加上括号; (3)当不等式两边都乘以同一个负数时,不等号的方向要改变
②去括号 乘法分配律、去括号法则 当括号前是“-”时,去掉括号后,原括号内的每一项都要变号
③移项 不等式的基本性质1 (1)所移的项要改变符号,不移的项不变号; (2)移项时,不等号的方向不改变
④合并同类项 合并同类项法则
⑤系数化为1 不等式的基本性质2、3 当不等式两边都乘以(或都除以)同一个负数时,不等号的方向要改变
三、课堂练习、巩固提高
1.下列式子:①;②;③;④;⑤;⑥.其中是一元一次不等式的有( )
A.1个 B.2个 C.3个 D.4个
2.不等式的解集是( )
A. B. C. D.
3.下列数中,能使不等式成立的的值为( )
A.1 B.2 C.3 D.4
4.若是关于x的一元一次不等式,则m=________.
选做题:
5.不等式的解集为________.
6.不等式的非负整数解有________个.
7.解不等式:
(1);(2);
【综合拓展类作业】
解不等式,并把解集在数轴上表示出来.
总结反思、拓展升华
【课堂总结】
知识点:
解一元一次不等式的一般步骤
(1)去分母——不等式性质2或3.
注意:①勿漏乘不含分母的项;②分子是两项或两项以上的代数式时要加括号;③若两边同时乘一个负数,要注意不等号的方向要改变.
(2)去括号——去括号法则和分配律.
注意:①勿漏乘括号内每一项;②括号前面是负号,括号内各项要变号.
(3)移项——移项法则(不等式的性质1).
注意:移项要变号.
(4)合并同类项——合并同类项法则.
(5)将未知数的系数化成1——不等式的性质2或3.
注意:两边同时除以未知数的系数时,要分清不等号的方向是否改变.
数学思想方法:
类比思想
五、【作业布置】
【知识技能类作业】
必做题:
1.下列不等式中不是一元一次不等式的是( )
A.2x>1 B.b<3 C.1-a≤a D.->1
2.已知|3-a|=a-3,则a的取值范围在数轴上表示正确的是( )
3.不等式3x-2>1的最小整数解是( )
A.0 B.1 C.2 D.3
4.若关于x的不等式mx-n>0的解集是x<,则关于x的不等式(m+n)x>n-m的解集是( )
A.x<- B.x>- C.x< D.x>
5.关于x的不等式m-≤1-x有正数解,m的值可以是________(写出一个即可).
选做题:
6.(1)解不等式:-1≤,把它的解集表示在数轴上;
(2)解不等式:<x+1,并把解集在数轴上表示出来.
已知关于x的不等式4x-3a>-1与2(x-1)+3>5的解集相同,求a的值.
8.已知整式的值为P.
(1)当m=1时,求P的值;
(2)若P的取值范围如图所示,求m的取值范围.
【综合拓展类作业】
9.关于x的不等式(2a-b)x>a-2b的解集是x<,求关于x的不等式ax+b<0的解集.
答案:
自学自测:
1.C 2.A 3.A
课堂练习:
1.B 2.D 3.A 4.2
5. 6.4
7.解:(1),
去括号,得.
移项,得.
合并同类项,得.
两边都除以2,得.
(2),
去分母,得,
去括号,得,
移项,得,
合并同类项,得,
两边都除以-5,得.
8.解:去分母,得.
去括号,得.
移项、合并同类项,得.
系数化为1,得.
这个不等式的解集在数轴上表示为:
作业布置:
1.D 解析:A.2x>1是一元一次不等式,不符合题意;B.b<3是一元一次不等式,不符合题意;C.1-a≤a是一元一次不等式,不符合题意;D.->1不是一元一次不等式,符合题意.故选D.
2.A 解析:∵|3-a|=a-3,
∴a-3≥0.∴a≥3.故选A.
3.C 解析:3x-2>1,解得x>1,x的最小整数解为2.故选C.
4.A 解析:∵关于x的不等式mx-n>0的解集是x<,∴m<0,=.∴m=5n.∴n<0.∴m+n<0.∴解关于x的不等式(m+n)x>n-m,得x<.∴x<=-.故选A.
5.0(答案不唯一) 解析:原不等式整理,得x≤1-m,
解得x≤2-2m.
∵原不等式有正数解,
∴2-2m>0.
解得m<1,
则m的值可以是0.(答案不唯一)
6.解:(1)-1≤,
去分母,得2(x+1)-6≤3(2-x).
去括号,得2x+2-6≤6-3x.
移项,得2x+3x≤6+6-2.
合并同类项,得5x≤10.
系数化为1,得x≤2.
其解集在数轴上表示如下:
(2)<x+1,
去分母,得x-1<2(x+1).
去括号,得x-1<2x+2.
移项,得x-2x<2+1.
合并同类项,得-x<3.
系数化为1,得x>-3.
其解集在数轴上表示如下:
7.解:由4x-3a>-1,得x>.
由2(x-1)+3>5,得x>2.
∵这两个不等式的解集相同,
∴=2,即3a-1=8.
∴a=3.
8.解:(1)当m=1时,
P=3=3×=4,
∴P的值是4.
(2)根据题意,得3≤7,
解得m≤2,
∴m的取值范围是m≤2.
9.解:由(2a-b)x>a-2b的解集是x<,可知2a-b<0,
即x<,所以=.所以b=8a.代入ax+b<0,得ax+8a<0.又因为2a-b<0,所以2a-8a<0.所以a>0.所以ax<-8a. 所以x<-8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
