第二十八章锐角三角函数 单元测试(无答案)人教版2024—2025学年九年级下册
文档属性
| 名称 | 第二十八章锐角三角函数 单元测试(无答案)人教版2024—2025学年九年级下册 | 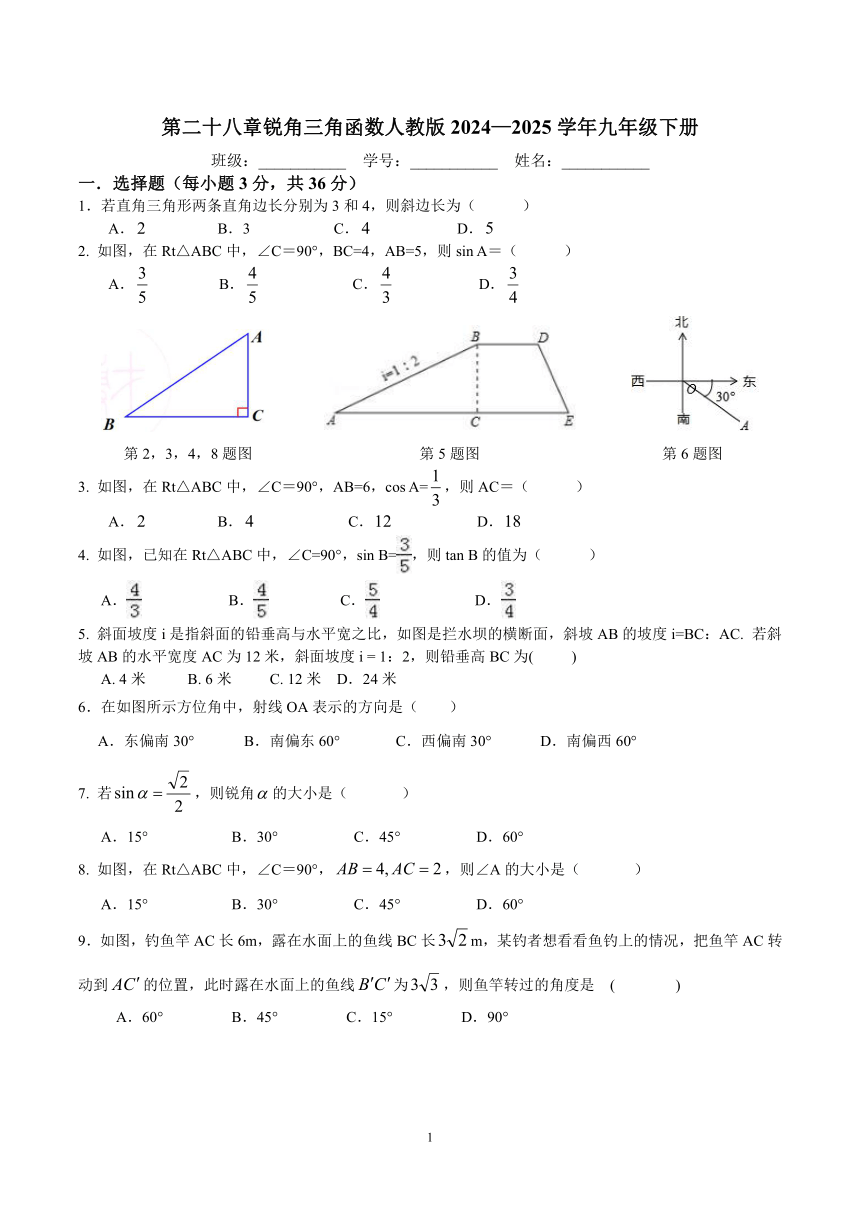 | |
| 格式 | docx | ||
| 文件大小 | 180.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-09 22:30:56 | ||
图片预览

文档简介
第二十八章锐角三角函数人教版2024—2025学年九年级下册
班级:___________ 学号:___________ 姓名:___________
一.选择题(每小题3分,共36分)
1.若直角三角形两条直角边长分别为3和4,则斜边长为( )
A. B.3 C. D.
2. 如图,在Rt△ABC中,∠C=90°,BC=4,AB=5,则sin A=( )
A. B. C. D.
第2,3,4,8题图 第5题图 第6题图
3. 如图,在Rt△ABC中,∠C=90°,AB=6,cos A=,则AC=( )
A. B. C. D.
4. 如图,已知在Rt△ABC中,∠C=90°,sin B=,则tan B的值为( )
A. B. C. D.
5. 斜面坡度i是指斜面的铅垂高与水平宽之比,如图是拦水坝的横断面,斜坡AB的坡度i=BC:AC. 若斜坡AB的水平宽度AC为12米,斜面坡度i = 1:2,则铅垂高BC为( )
A. 4米 B. 6米 C. 12米 D.24米
6.在如图所示方位角中,射线OA表示的方向是( )
A.东偏南30° B.南偏东60° C.西偏南30° D.南偏西60°
7. 若,则锐角的大小是( )
A.15° B.30° C.45° D.60°
8. 如图,在Rt△ABC中,∠C=90°,,则∠A的大小是( )
A.15° B.30° C.45° D.60°
9.如图,钓鱼竿AC长6m,露在水面上的鱼线BC长m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到的位置,此时露在水面上的鱼线为,则鱼竿转过的角度是 ( )
A.60° B.45° C.15° D.90°
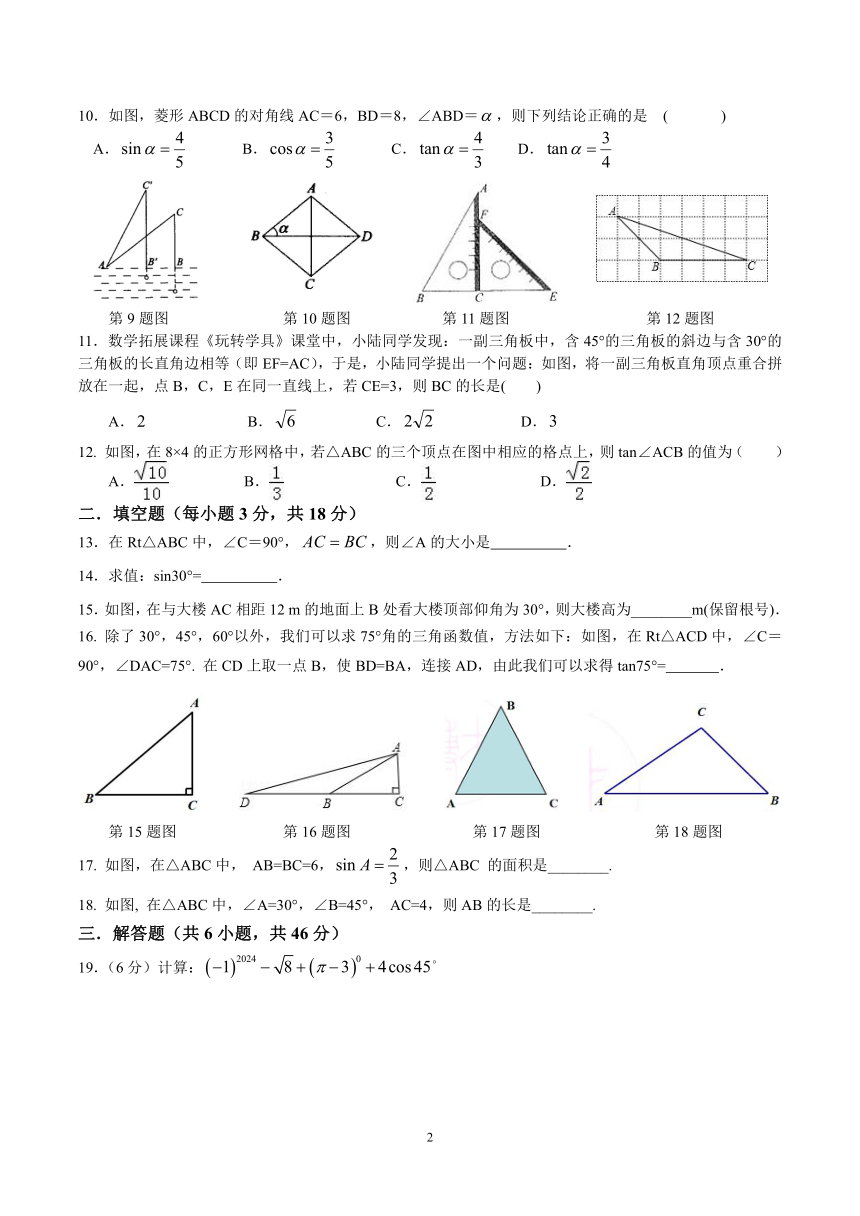
10.如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=,则下列结论正确的是 ( )
A. B. C. D.
第9题图 第10题图 第11题图 第12题图
11.数学拓展课程《玩转学具》课堂中,小陆同学发现:一副三角板中,含45°的三角板的斜边与含30°的三角板的长直角边相等(即EF=AC),于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点B,C,E在同一直线上,若CE=3,则BC的长是( )
A. B. C. D.
12. 如图,在8×4的正方形网格中,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
A. B. C. D.
二.填空题(每小题3分,共18分)
13.在Rt△ABC中,∠C=90°,,则∠A的大小是 .
14.求值:sin30°= .
15.如图,在与大楼AC相距12 m的地面上B处看大楼顶部仰角为30°,则大楼高为________m(保留根号).
16. 除了30°,45°,60°以外,我们可以求75°角的三角函数值,方法如下:如图,在Rt△ACD中,∠C=90°,∠DAC=75°. 在CD上取一点B,使BD=BA,连接AD,由此我们可以求得tan75°= .
第15题图 第16题图 第17题图 第18题图
17. 如图,在△ABC中, AB=BC=6,,则△ABC 的面积是________.
18. 如图, 在△ABC中,∠A=30°,∠B=45°, AC=4,则AB的长是________.
三.解答题(共6小题,共46分)
19.(6分)计算:
20.(6分)如图,在△ABC中,AD⊥BC,AE是BC边上的中线,AB=10,AD=6,tan∠ACB=1.
(1)求BC的长;
(2)求sin∠DAE的值.
21.(8分)为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表.
组别 分数段 频次 频率
A 60≤x<70 17 0.17
B 70≤x<80 30 a
C 80≤x<90 b 0.45
D 90≤x<100 8 0.08
请根据所给信息,解答以下问题:
(1)表中a= ,b= ;
(2)扇形统计图中B组对应扇形的圆心角的度数是________;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率.
22.(8分)如图,△ABC中,∠C=900,BD平分∠ABC,BC=6,BD=,求∠A的度数及AD的长.
23.(9分)瑞天时代广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的倾斜角为18°,一楼到地下停车场地面的垂直高度CD=3m,一楼到地平线的距离BC=1m.
(1)为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?
(2)如果给该购物广场送货的货车高度为2.6m,那么按这样的设计能否保证货车顺利进入地下停车场?并说明理由.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
24.(9分)如图,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.
(1)若AE=1,求△ABD的周长;
(2)若AD=BD,求tan∠ABC的值.
班级:___________ 学号:___________ 姓名:___________
一.选择题(每小题3分,共36分)
1.若直角三角形两条直角边长分别为3和4,则斜边长为( )
A. B.3 C. D.
2. 如图,在Rt△ABC中,∠C=90°,BC=4,AB=5,则sin A=( )
A. B. C. D.
第2,3,4,8题图 第5题图 第6题图
3. 如图,在Rt△ABC中,∠C=90°,AB=6,cos A=,则AC=( )
A. B. C. D.
4. 如图,已知在Rt△ABC中,∠C=90°,sin B=,则tan B的值为( )
A. B. C. D.
5. 斜面坡度i是指斜面的铅垂高与水平宽之比,如图是拦水坝的横断面,斜坡AB的坡度i=BC:AC. 若斜坡AB的水平宽度AC为12米,斜面坡度i = 1:2,则铅垂高BC为( )
A. 4米 B. 6米 C. 12米 D.24米
6.在如图所示方位角中,射线OA表示的方向是( )
A.东偏南30° B.南偏东60° C.西偏南30° D.南偏西60°
7. 若,则锐角的大小是( )
A.15° B.30° C.45° D.60°
8. 如图,在Rt△ABC中,∠C=90°,,则∠A的大小是( )
A.15° B.30° C.45° D.60°
9.如图,钓鱼竿AC长6m,露在水面上的鱼线BC长m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到的位置,此时露在水面上的鱼线为,则鱼竿转过的角度是 ( )
A.60° B.45° C.15° D.90°
10.如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=,则下列结论正确的是 ( )
A. B. C. D.
第9题图 第10题图 第11题图 第12题图
11.数学拓展课程《玩转学具》课堂中,小陆同学发现:一副三角板中,含45°的三角板的斜边与含30°的三角板的长直角边相等(即EF=AC),于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点B,C,E在同一直线上,若CE=3,则BC的长是( )
A. B. C. D.
12. 如图,在8×4的正方形网格中,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
A. B. C. D.
二.填空题(每小题3分,共18分)
13.在Rt△ABC中,∠C=90°,,则∠A的大小是 .
14.求值:sin30°= .
15.如图,在与大楼AC相距12 m的地面上B处看大楼顶部仰角为30°,则大楼高为________m(保留根号).
16. 除了30°,45°,60°以外,我们可以求75°角的三角函数值,方法如下:如图,在Rt△ACD中,∠C=90°,∠DAC=75°. 在CD上取一点B,使BD=BA,连接AD,由此我们可以求得tan75°= .
第15题图 第16题图 第17题图 第18题图
17. 如图,在△ABC中, AB=BC=6,,则△ABC 的面积是________.
18. 如图, 在△ABC中,∠A=30°,∠B=45°, AC=4,则AB的长是________.
三.解答题(共6小题,共46分)
19.(6分)计算:
20.(6分)如图,在△ABC中,AD⊥BC,AE是BC边上的中线,AB=10,AD=6,tan∠ACB=1.
(1)求BC的长;
(2)求sin∠DAE的值.
21.(8分)为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表.
组别 分数段 频次 频率
A 60≤x<70 17 0.17
B 70≤x<80 30 a
C 80≤x<90 b 0.45
D 90≤x<100 8 0.08
请根据所给信息,解答以下问题:
(1)表中a= ,b= ;
(2)扇形统计图中B组对应扇形的圆心角的度数是________;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率.
22.(8分)如图,△ABC中,∠C=900,BD平分∠ABC,BC=6,BD=,求∠A的度数及AD的长.
23.(9分)瑞天时代广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的倾斜角为18°,一楼到地下停车场地面的垂直高度CD=3m,一楼到地平线的距离BC=1m.
(1)为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?
(2)如果给该购物广场送货的货车高度为2.6m,那么按这样的设计能否保证货车顺利进入地下停车场?并说明理由.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
24.(9分)如图,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.
(1)若AE=1,求△ABD的周长;
(2)若AD=BD,求tan∠ABC的值.
