2.1两条直线的位置关系 课件(共13张PPT) 2024-2025学年北师版数学七年级下册
文档属性
| 名称 | 2.1两条直线的位置关系 课件(共13张PPT) 2024-2025学年北师版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 10:51:35 | ||
图片预览




文档简介
(共13张PPT)
2.1 两条直线的位置关系(1)
第二章 相交线与平行线
新课导入
情境引入
请同学们观察下列图片,在同一平面内,两条直线有哪些位置关系?
总结:在同一平面内,两条直线的位置关系有 和 两种。
若两条直线 ,我们称这两条直线为相交线。
同一平面内, 的两条直线为平行线。
相交
平行
只有一个公共点
不相交
新课导入
例1 下列说法正确的是( )
A.不相交的两条直线是平行线
B.在同一平面内,不相交的两条射线是平行线
C.在同一平面内,两条直线不相交就重合
D.在同一平面内,没有公共点的两条直线是平行线
D
新课讲授
探究一:对顶角的概念与性质
新课讲授
探究一:对顶角的概念与性质
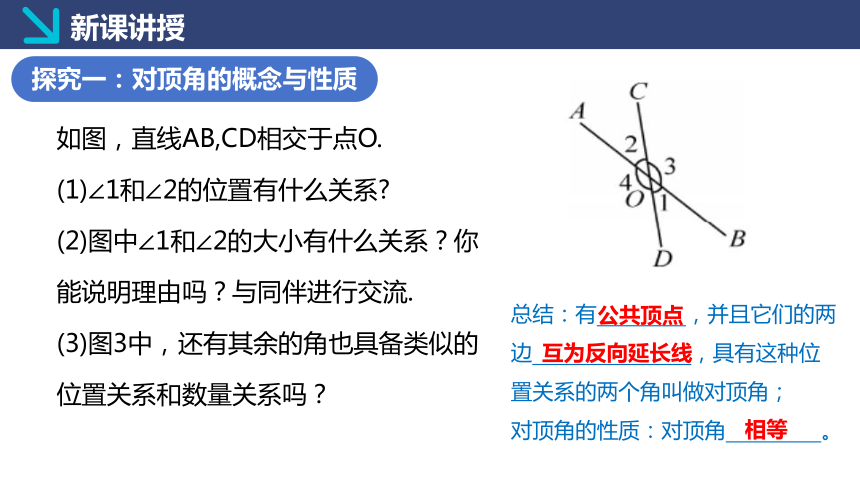
如图,直线AB,CD相交于点O.
(1)∠1和∠2的位置有什么关系
(2)图中∠1和∠2的大小有什么关系?你能说明理由吗?与同伴进行交流.
(3)图3中,还有其余的角也具备类似的位置关系和数量关系吗?
总结:有 ,并且它们的两边 ,具有这种位置关系的两个角叫做对顶角;
对顶角的性质:对顶角 。
公共顶点
互为反向延长线
相等
新课讲授
探究一:对顶角的概念与性质
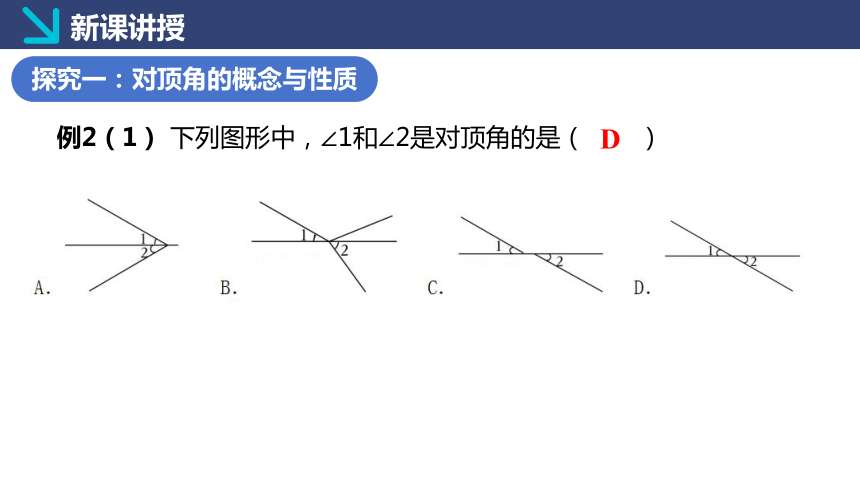
例2(1) 下列图形中,∠1和∠2是对顶角的是( )
D
新课讲授
探究一:对顶角的概念与性质
例2(2)如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件圆心角的度数为 。
40°
新课讲授
探究二:补角的概念与性质
如图,直线AB与CD 相交于点O。
(1)∠1与∠3有什么数量关系呢?
(2)图中还有其他的角也具备这样的数量关系吗?
总结:一般地,如果两个角的和是 ,那么称这两个角互为 。
180°
补角
新课讲授
探究二:补角的概念与性质
我们发现:同角(或等角)的 相等
注意:“同角”指的是同一个角,“等角”指的是相等的角.
补角
新课讲授
探究二:补角的概念与性质
例3(1)如图所示,直线AB,CD,EF 相交于点O,则∠AOC 的对顶角是 ,∠AOC 的补角是 ;
若∠AOC=50°,则∠BOD= ,∠COB= .
(2)一个角的补角比这个角的6倍还大5°,则这个角的大小为 。
∠BOD
∠BOC,∠AOD
50°
130°
25°
新课讲授
探究三:余角的概念与性质
如果两个角的和是 ,那么称这两个角互为余角。
结论:同角(或等角)的 相等
操作 交流
尝试将一副直角三角板的直角顶点重合,如何摆放三角板可以得到“同角的余角相等”?
90°
余角
课堂小结
两条直线的位置关系1
相交线与平行线
同一平面内两条直线的位置关系:相交和平行.
若两条直线只有一个公共点,我们称这两条直线为相交线.在同一平面内,不相交的两条直线叫平行线.
对顶角
如果两个角有公共顶点,并且它们的两边互为反向延长线,那么这两个角做对顶角.
性质:对顶角相等.
余角和补角
如果两个角的和为180°,那么称这两个角互为补角;
如果两个角的和为90°,那么称这两个角互为余角.
性质:同角或等角的补角相等,
同角或等角的余角相等.
作业
习题2.1 第1、4、5、9题
2.1 两条直线的位置关系(1)
第二章 相交线与平行线
新课导入
情境引入
请同学们观察下列图片,在同一平面内,两条直线有哪些位置关系?
总结:在同一平面内,两条直线的位置关系有 和 两种。
若两条直线 ,我们称这两条直线为相交线。
同一平面内, 的两条直线为平行线。
相交
平行
只有一个公共点
不相交
新课导入
例1 下列说法正确的是( )
A.不相交的两条直线是平行线
B.在同一平面内,不相交的两条射线是平行线
C.在同一平面内,两条直线不相交就重合
D.在同一平面内,没有公共点的两条直线是平行线
D
新课讲授
探究一:对顶角的概念与性质
新课讲授
探究一:对顶角的概念与性质
如图,直线AB,CD相交于点O.
(1)∠1和∠2的位置有什么关系
(2)图中∠1和∠2的大小有什么关系?你能说明理由吗?与同伴进行交流.
(3)图3中,还有其余的角也具备类似的位置关系和数量关系吗?
总结:有 ,并且它们的两边 ,具有这种位置关系的两个角叫做对顶角;
对顶角的性质:对顶角 。
公共顶点
互为反向延长线
相等
新课讲授
探究一:对顶角的概念与性质
例2(1) 下列图形中,∠1和∠2是对顶角的是( )
D
新课讲授
探究一:对顶角的概念与性质
例2(2)如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件圆心角的度数为 。
40°
新课讲授
探究二:补角的概念与性质
如图,直线AB与CD 相交于点O。
(1)∠1与∠3有什么数量关系呢?
(2)图中还有其他的角也具备这样的数量关系吗?
总结:一般地,如果两个角的和是 ,那么称这两个角互为 。
180°
补角
新课讲授
探究二:补角的概念与性质
我们发现:同角(或等角)的 相等
注意:“同角”指的是同一个角,“等角”指的是相等的角.
补角
新课讲授
探究二:补角的概念与性质
例3(1)如图所示,直线AB,CD,EF 相交于点O,则∠AOC 的对顶角是 ,∠AOC 的补角是 ;
若∠AOC=50°,则∠BOD= ,∠COB= .
(2)一个角的补角比这个角的6倍还大5°,则这个角的大小为 。
∠BOD
∠BOC,∠AOD
50°
130°
25°
新课讲授
探究三:余角的概念与性质
如果两个角的和是 ,那么称这两个角互为余角。
结论:同角(或等角)的 相等
操作 交流
尝试将一副直角三角板的直角顶点重合,如何摆放三角板可以得到“同角的余角相等”?
90°
余角
课堂小结
两条直线的位置关系1
相交线与平行线
同一平面内两条直线的位置关系:相交和平行.
若两条直线只有一个公共点,我们称这两条直线为相交线.在同一平面内,不相交的两条直线叫平行线.
对顶角
如果两个角有公共顶点,并且它们的两边互为反向延长线,那么这两个角做对顶角.
性质:对顶角相等.
余角和补角
如果两个角的和为180°,那么称这两个角互为补角;
如果两个角的和为90°,那么称这两个角互为余角.
性质:同角或等角的补角相等,
同角或等角的余角相等.
作业
习题2.1 第1、4、5、9题
同课章节目录
