北师大版数学九年级上册第五章第3节《反比例函数的应用》课时练习
文档属性
| 名称 | 北师大版数学九年级上册第五章第3节《反比例函数的应用》课时练习 |  | |
| 格式 | doc | ||
| 文件大小 | 579.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-11 16:48:36 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
北师大版数学九年级上册第5章第3节反比例函数的应用同步检测
一、选择题
1.如图,下列各种情境分别可以用那幅图来近似地刻画一杯越来越凉的水(水温与时间的关系)( )
A.
B.
C.
D.
答案:C
解析:解答:A.热水放出热量,温度先升高后降低.不符合题意.
B.热水放在空气中,不断放出热量,温度保持不变.不符合题意.
C.热水放出热量,温度不断降低.符合题意.
D.热水放出热量,温度不断升高.不符合题意.
故选:C.
分析:此题考查了反比例函数的应用,理解题意和反比例函数图象的形状是解题关键.温度是表示物体冷热程度的物理量.一杯水越来越凉,说明温度越来越低.
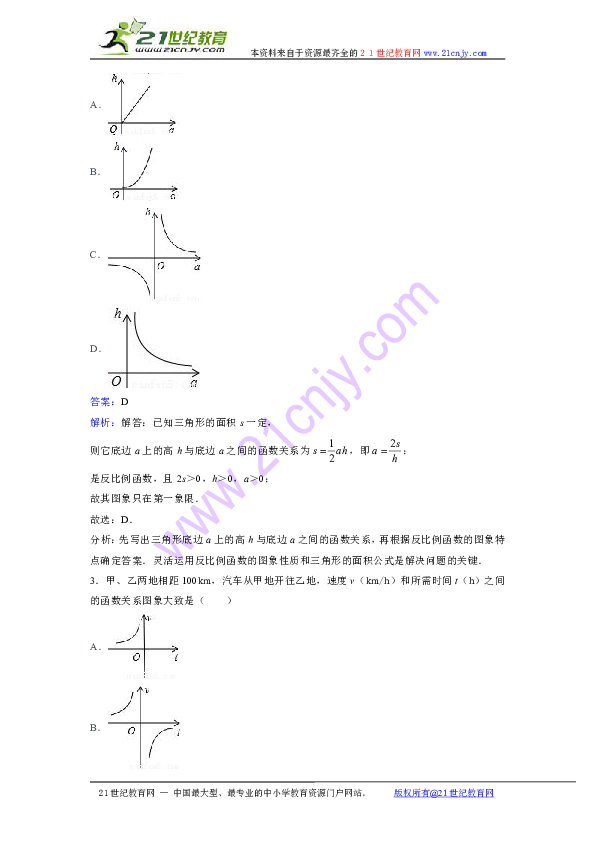
2.如图,已知三角形的面积一定,则其底边a和该底边上的高h之间的函数关系图象大致是( )
A.
B.
C.
D.
答案:D
解析:解答:已知三角形的面积s一定,
则它底边a上的高h与底边a之间的函数关系为,即;
是反比例函数,且2s>0,h>0,a>0;
故其图象只在第一象限.
故选:D.
分析:先写出三角形底边a上的高h与底边a之间的函数关系,再根据反比例函数的图象特点确定答案.灵活运用反比例函数的图象性质和三角形的面积公式是解决问题的关键.
3.甲、乙两地相距100km,汽车从甲地开往乙地,速度v(km/h)和所需时间t(h)之间的函数关系图象大致是( )
A.
B.
C.
D.
答案:C
解析:解答:根据题意得100=vt,
∴(t>0),
其图象在第一象限,
故选:C.
分析:根据“路程=速度×时间”列出关系式,经过转化即可得到相应函数关系式,即可判断出图象所在象限.双曲线,当k>0时经过第一、三象限,当k<0时经过第二、四象限.
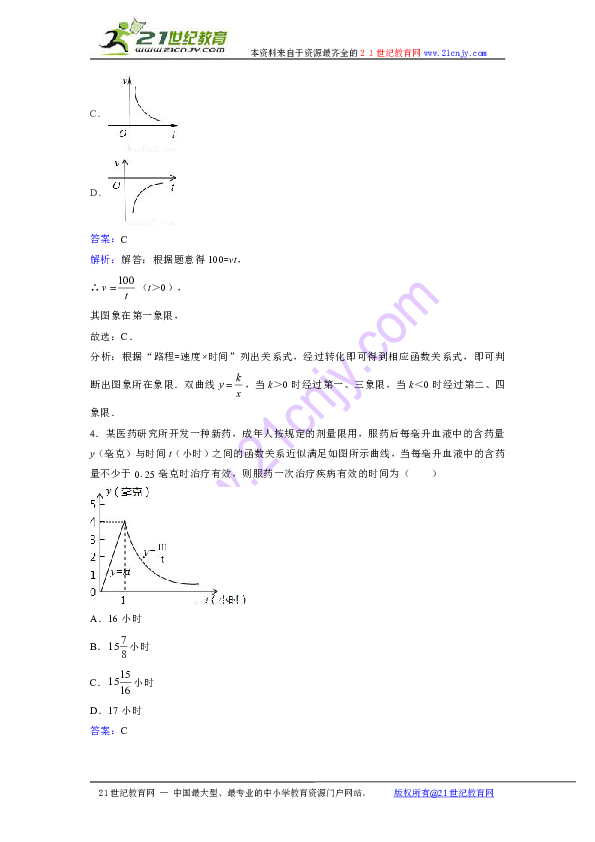
4.某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为( )
A.16小时
B.小时
C.小时
D.17小时
答案:C
解析:解答:把点(1,4)分别代入y=kt,中,得k=4,m=4,
∴y=4t,,
把y=0.25代入y=4t中,得,
把y=0.25代入中,得,
∴治疗疾病有效的时间为:;
故选:C.
分析:将点(1,4)分别代入y=kt,中,求k、m,确定函数关系式,再把y=0.25代入两个函数式中求t,把所求两个时间t作差即可.灵活掌握反比例函数的图象性质的应用.
5.一个菱形的面积是4,则这个菱形的两条对角线长y与x的函数关系的图象大致是( )A.
B.
C.
D.
答案:C
解析:解答:根据菱形的面积公式:xy÷2=4,解得,y是x的反比例函数,x>0,y>0,
∴反比例函数的图象在第一象限.
故选:C.
分析:菱形的面积=对角线乘积的一半,列出关系式,写出y与x的函数关系式,根据变量的取值,确定函数所在的象限就可以确定函数的图象.
题型:单选题
6.矩形面积为4,它的一边长y与邻边长x的函数关系用图象表示大致是( )
A.
B.
C.
D.
答案:A
解析:解答:∵xy=4
∴(x>0,y>0)
故选:A.
分析:根据题意有:xy=4;故y与x之间的函数图象为反比例函数,且根据x、y实际意义x、y应大于0;从而得出答案.本题考查了反比例函数(k≠0)的图象与性质的应用.
7.蓄电池的电压为定值,使用此电源时,电流I(A)是电阻R(Ω)的反比例函数,其图象如图所示,当R为10Ω时,电流I是( )
A.3A
B.3.6A
C.4A
D.6A
答案:B
解析:解答:∵电流I(A)是电阻R(Ω)的反比例函数
∴设(k≠0)
把(4,9)代入得:k=4×9=36
∴
当R=10时,
I=36÷10=3.6A,
故选:B.
分析:根据电流I(A)是电阻R(Ω)的反比例函数,首先设出(k≠0),然后把(4,9)代入求出k的值,最后代入R=10求得I.
8.如图,一次函数y=-2x+b的图象与反比例函数的图象交于点A(1,6)、B(3,2)两点.b的值为( )
A.5
B.6
C.7
D.8
答案:D
解析:解答:把A(1,6)代入y=-2x+b得,
-2+b=6,
∴b=8;
故选:D.
分析:把A(1,6)代入y=-2x+b即可求得b的值;易错点是利用反例函数解析式求出k的值,错选B.
9.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V()的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
A.不小于
B.小于
C.不小于
D.小于
答案:C
解析:解答:设球内气体的气压P(kPa)和气体体积V()的关系式为,
∵图象过点(1.6,60)
∴k=96
即
在第一象限内,P随V的增大而减小,
∴当P≤120时,≥.
故选:C.
分析:根据题意可知温度不变时,气球内气体的气压P(kPa)是气体体积V()的反比例函数,且过点(1.6,60)所以P V=96;故当P≤120时,可以判断V不小于.根据图象上的已知点的坐标和实际问题,利用待定系数法求出函数解析式是解题的关键.
10.为了预防“HINI”流感,某校对教室进行药熏消毒,药品燃烧时,室内每立方米的含药量与时间成正比;燃烧后,室内每立方米含药量与时间成反比,则消毒过程中室内每立方米含药量y与时间t的函数关系图象大致为( )
A.
B.
C.
D.
答案:A
解析:解答:由正比例函数和反比例函数的图象性质,可判断:消毒过程中室内每立方米含药量y与时间t的函数关系图象大致为A.
故选:A.
分析:主要利用正比例函数和反比例函数的图象性质解答.正比例函数的图象是一条直线,反比例函数的图象是双曲线.
11.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( )
A.
B.
C.
D.
答案:A
解析:解答:∵是剪去的两个矩形,两个矩形的面积和为20,
∴xy=10,
∴y是x的反比例函数,
∵2≤x≤10,
∴答案为A.
故选:A.
分析:先根据图形的剪切确定变化过程中的函数关系式,确定函数类型,再根据自变量及函数的取值范围确定函数的具体图象.现实生活中存在大量成反比例函数的两个变量,确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限是解答该类问题的关键.
12.如图,反比例函数的一个分支与⊙O有两个交点A,B,且这个分支平分⊙O,以下说法正确的是( )
A.反比例函数的这个分支必过圆心O
B.劣弧AB等于120度
C.反比例函数的这个分支把⊙O的面积平分
D.反比例函数的这个分支把⊙O的周长平分
答案:D
解析:解答:A.反比例函数的这个分支不可能过圆心O,否则无法平分圆,所以错误;
B.劣弧AB等于180°,所以错误;
C.反比例函数的这个分支不能把⊙O的面积平分,所以错误;
D.这个分支平分⊙O,即反比例函数的这个分支把⊙O的周长平分,D正确.
故选:D.
分析:根据题意:这个分支平分⊙O,即反比例函数的这个分支把⊙O的周长平分可判断D正误.C一定错误,B中,根据劣弧AB等于180度判断.A中根据反比例函数的这个分支不可能过圆心O,否则无法平分圆,由此判断.本题考查反比例函数性质的运用,分别讨论判断正误.
13.一个圆锥的侧面展开图是一个面积为4平方单位的扇形,那么这个圆锥的母线长l与底面半径x之间的函数关系用图象表示大致是( )
A.
B.
C.
D.
答案:C
解析:解答:因为扇形面积为
,可得.
故选:C.
分析:先利用扇形的面积公式计算,再转化出圆锥的母线长l与底面半径x之间的函数关系.此题的关键是从扇形面积公式,转化出圆锥的母线长l与底面半径x之间的函数关系.熟悉反比例函数的图象也很关键.
14.如图,在直角坐标系中,有菱形OABC,A点的坐标是(10,0),双曲线(x>0)经过点C,且OB AC=160,则k的值为( )
A.40
B.48
C.64
D.80
答案:B
解析:解答:∵四边形OABC是菱形,OB与AC为两条对角线,且OB AC=160,
∴菱形OABC的面积为80,即OA CD=80,
∵OA=AC=10,
∴CD=8,
在Rt△OCD中,OC=10,CD=8,
根据勾股定理得:OD=6,即C(6,8),
则k的值为48.
故选:B.
分析:过C作CD垂直于x轴,交x轴于点D,由菱形的面积等于对角线乘积的一半,根据已知OB与AC的乘积求出菱形OABC的面积,而菱形的面积可以由OA乘以CD来求,根据OA的长求出CD的长,在直角三角形OCD中,利用勾股定理求出OD的长,确定出C的坐标,代入反比例解析式中可求出k的值.此题属于反比例函数综合题,涉及的知识有:菱形的性质,勾股定理,以及坐标与图形性质,求出C的坐标是解答本题的关键.
15.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:20
B.7:30
C.7:45
D.7:50
答案:A
解析:解答:∵开机加热时每分钟上升10℃,
∴从30℃到100℃需要7分钟,
设一次函数关系式为:y=k1x+b,
将(0,30),(7,100)代入y=k1x+b得k1=10,b=30
∴y=10x+30(0≤x≤7),令y=50,解得x=2;
设反比例函数关系式为:,
将(7,100)代入得k=700,
∴,
将y=30代入,解得;
∴(7≤x≤),令y=50,解得x=14.
所以,饮水机的一个循环周期为分钟.每一个循环周期内,在0≤x≤2及14≤x≤时间段内,水温不超过50℃.
逐一分析如下:
选项A:7:20至8:45之间有85分钟.85-×3=15,位于14≤x≤时间段内,故可行;
选项B:7:30至8:45之间有75分钟.75-×3=5,不在0≤x≤2及14≤x≤时间段内,故不可行;
选项C:7:45至8:45之间有60分钟.60-×2=≈13.3,不在0≤x≤2及14≤x≤时间段内,故不可行;
选项D:7:50至8:45之间有55分钟.55-×2=≈8.3,不在0≤x≤2及14≤x≤时间段内,故不可行.
综上所述,四个选项中,唯有7:20符合题意.
故选:A.
分析:第1步:求出两个函数的解析式;第2步:求出饮水机完成一个循环周期所需要的时间;第3步:求出每一个循环周期内,水温不超过50℃的时间段;第4步:结合4个选择项,逐一进行分析计算,得出结论.此题主要考查了一次函数及反比例函数的应用题,还有时间的讨论问题.关键要认真审题,理解题意.
二、填空题
16.你吃过兰州拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度ycm是面条粗细(横截面积)xcm2的反比例函数.假设它的图象如图所示,则y与x的函数表达式为______ .
答案:(x>0)
解析:解答:设反比例函数图象的解析式为,
由图可得,反比例函数上一点坐标为(0.04,3200)代入,有k=0.04×3200=128,
又题中实际意义需x>0.
∴(x>0).
故答案为:(x>0).
分析:根据反比例函数图象,设解析式为,由于点(0.04,3200)在图象上,代入反比例函数求得k的值.
17.一种新型汽车可装汽油500L,若汽车每小时用油量为xL.
①用油时间yh与每小时的用油量xL之间的函数表达式可表示为______;
答案:
②每小时的用油量为25L,则这些油可用的时间为______;
答案:20
③如果要使汽车连续行驶50h不需加油,那么每小时用油量的取值范围是______.
答案:0≤x<10
解析:解答:①∵可装汽油500L,若汽车每小时用油量为xL,
∴用油时间yh与每小时的用油量xL之间的函数表达式可表示为;
②每小时的用油量为25L,则这些油可用的时间为500÷25=20小时;
③如果要使汽车连续行驶50h不需加油,那么每小时用油量的取值范围0≤x<10;
故答案为:;20;0≤x<10;
分析:用总量除以每小时的用油量即可列出算式,代入有关数据求解即可.由反比例函数的图象的性质,进行解答.
18.小强欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为1000牛顿和0.5米,则当动力臂为1米时,撬动石头至少需要的力为 牛顿.
答案:500
解析:解答:由杠杆平衡条件可知:
=,
即:×1m=1000N×0.5m,
=500N
答案为:500.
分析:根据杠杆平衡条件=,代入有关数据即可.
19.如图,在平面直角坐标系中,在x轴上代表初始值x的那个点沿着竖线走,直到和曲线(x>0)交于点P后,在交点P处沿着东南方向(南偏东45°)走,一直和x轴相交,这个交点称投影点T.当x=1时,有P(1,4),相应的投影点T的坐标是(5,0);当x=2时,有P(2,2),相应的投影点T的坐标是(4,0);若投影点T的坐标是(,0)时,初始值x= .
答案:19
解析:解答:∵当x=1时,有P(1,4),相应的投影点T的坐标是(5,0);当x=2时,有P(2,2),相应的投影点T的坐标是(4,0);
∴1+4=5,2+2=4,
∴若投影点T的坐标是(,0)时,即x+=,
解得:x=19.
故答案为:19.
分析:根据已知数据得出投影点与P点坐标的关系,从而得出答案.
20.已知一定质量的二氧化碳的密度ρ(kg/)与体积V()成反比例函数关系,且当V=3.3时,ρ=3kg/;若要求二氧化碳的密度不超过1.5kg/,则体积V的变化范围是
答案:0≤v≤6.6
解析:解答:设二氧化碳的密度ρ(kg/)与体积V()之间的函数关系为,
∵当V=3.3时,ρ=3kg/;
∴m=ρV=3.3×3=9.9kg,
∴,
当ρ=1.5kg/时,
=6.6
故答案为:0≤v≤6.6.
分析:首先求出ρ与体积V之间的函数关系,然后根据密度的值确定体积的变化范围.
三、解答题
21.某商场出售一批名牌衬衣,衬衣进价为80元,在营销中发现,该衬衣的日销售量y(件)是日销售价x(元)的反比例函数,且当售价定为100元/件时,每日可售出30件.
(1)请求出y与x之间的函数关系式.
答案:
(2)若商场计划经营此种衬衣的日销售利润为2000元,则其单价应定为多少元?
答案:240
解析:解答:(1)设函数式为(k≠0).
,
k=3000
.
(2)单价是x元,
y(x-80)=2000
(x-80)=2000,
解得:x=240,
故单价定为 240元.
分析:(1)因为y与x成反比例函数关系,可设出函数式(k≠0),然后根据当售价定为100元/件时,每天可售出30件可求出k的值;(2)设单价是x元,根据每天可售出y件,每件的利润是(x-80)元,总利润为2000元,根据利润=售价-进价可列方程求解.
22.学校锅炉旁建有一个储煤库,开学初购进一批煤,现在知道:按每天用煤0.6吨计算,一学期(按150天计算)刚好用完.若每天的耗煤量为x吨,那么这批煤能维持y天.
(1)则y与x之间有怎样的函数关系?
答案:
(2)若每天节约0.1吨,则这批煤能维持多少天?
答案:180
解析:解答:(1)煤的总量为:0.6×150=90吨,
∵x y=90
∴;
(2)∵每天节约0.1吨煤,
∴每天的用煤量为0.6-0.1=0.5吨,
∴=180(天),
∴这批煤能维持180天.
分析:(1)首先求得煤的总量,然后利用耗煤量乘以天数等于煤总量得出函数关系式;(2)将每天的用煤量代入求得的函数解析式得到答案.
23.某汽车油箱的容积为70升,小王把油箱注满油后准备驾驶汽车从县城到300千米外的省城接待客人,在接到客人后立即按原路返回,请回答下列问题:
(1)油箱注满油后,汽车能够行使的总路程y(单位:千米)与平均耗油量x(单位:升/千米)之间有怎样的函数关系?
答案:(x>0)
(2)如果小王以平均每千米耗油0.1升的速度驾驶汽车到达省城,在返程时由于下雨,小王降低了车速,此时每行驶1千米的耗油量增加了一倍,如果小王一直以此速度行驶,邮箱里的油是否够回到县城?如果不够用,至少还需加多少油?
答案:不够用|20升
解析:解答:(1)∵耗油量×行驶里程=70升;
∴xy=70
∴(x>0);
(2)不够用,理由如下:
∵0.1×300=30(升) 0.2×300=60(升),
∴30+60>70 故不够用
30+60-70=20(升)
答:不够用,到县城至少还需加20升油.
分析:(1)根据耗油量×行驶里程=70升列出函数关系式即可;(2)分别求得每千米好友0.1升的速度的耗油量和0.2升的耗油量,与70比较即可得到答案.正确确定函数解析式是解题的关键.
24.如图是某电脑公司2011年的销售额y(万元)关于时间x(月)之间的函数图象,其中前几个月两变量之间满足反比例函数关系,后几个月两变量之间满足一次函数关系,观察图象,回答下列问题:
(1)该年度______月份的销售额最低;
答案:5
(2)求出该年度最低的销售额;
答案:5万元
(3)若电脑公司月销售额不大于10万元,则称销售处于淡季.在2011年中,该电脑公司哪几个月销售处于淡季?
答案:3月、4月、5月和6月这四个月
解析:解答:(1)观察函数图象知:5月份的销售额最低;
(2)当1≤x≤5时,设反比例函数的解析式为,
由题意得反比例函数的图象经过点(1,25)
∴
解得:k=25,
∴反比例函数的解析式为,
当x=5时,(万元)
答:该年度最低的销售额为5万元.
(3)当1≤x≤5时,若y≤10时,有≤10
∴x≥2.5
当5≤x≤12时,设函数解析式为y=kx+b
由题意得:
∴一次函数的解析式为y=5x-20
当5≤x≤12时,若y≤10,得:x≤6
∴当2.5≤x≤6的整数时,销售处于淡季.
即在2011年3月、4月、5月和6月这四个月,该电脑公司销售处于淡季.
分析:(1)直接观察图象即可得到答案;(2)求得反比例函数的解析式后即可求得5月份的最低销售额;(3)求得一次函数的解析式后利用自变量的取值范围确定答案即可.此题考查了反比例函数图象的性质、待定系数法求反比例函数解析式以及反比例函数图象上点的坐标特征.
25.心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第5分钟时与第30分钟时相比较,何时学生的注意力更集中?
答案:第30分钟
(2)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
答案:能
解析:解答:(1)设线段AB所在的直线的解析式为,
把B(10,40)代入得,=2,
∴.
设C、D所在双曲线的解析式为,
把C(25,40)代入得,=1000,
∴
当=5时,=2×5+20=30,
当=30时,,
∴<
∴第30分钟注意力更集中.
(2)令=36,
∴36=2x+20,
∴=8
令=36,
∴,
∴≈27.8
∵27.8-8=19.8>19,
∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
分析:(1)先用代定系数法分别求出AB和CD的函数表达式,再分别求第五分钟和第三十分钟的注意力指数,最后比较判断;(2)分别求出注意力指数为36时的两个时间,再将两时间之差和19比较,大于19则能讲完,否则不能.主要考查了函数的应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式,再根据自变量的值求算对应的函数值.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
北师大版数学九年级上册第5章第3节反比例函数的应用同步检测
一、选择题
1.如图,下列各种情境分别可以用那幅图来近似地刻画一杯越来越凉的水(水温与时间的关系)( )
A.
B.
C.
D.
答案:C
解析:解答:A.热水放出热量,温度先升高后降低.不符合题意.
B.热水放在空气中,不断放出热量,温度保持不变.不符合题意.
C.热水放出热量,温度不断降低.符合题意.
D.热水放出热量,温度不断升高.不符合题意.
故选:C.
分析:此题考查了反比例函数的应用,理解题意和反比例函数图象的形状是解题关键.温度是表示物体冷热程度的物理量.一杯水越来越凉,说明温度越来越低.
2.如图,已知三角形的面积一定,则其底边a和该底边上的高h之间的函数关系图象大致是( )
A.
B.
C.
D.
答案:D
解析:解答:已知三角形的面积s一定,
则它底边a上的高h与底边a之间的函数关系为,即;
是反比例函数,且2s>0,h>0,a>0;
故其图象只在第一象限.
故选:D.
分析:先写出三角形底边a上的高h与底边a之间的函数关系,再根据反比例函数的图象特点确定答案.灵活运用反比例函数的图象性质和三角形的面积公式是解决问题的关键.
3.甲、乙两地相距100km,汽车从甲地开往乙地,速度v(km/h)和所需时间t(h)之间的函数关系图象大致是( )
A.
B.
C.
D.
答案:C
解析:解答:根据题意得100=vt,
∴(t>0),
其图象在第一象限,
故选:C.
分析:根据“路程=速度×时间”列出关系式,经过转化即可得到相应函数关系式,即可判断出图象所在象限.双曲线,当k>0时经过第一、三象限,当k<0时经过第二、四象限.
4.某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为( )
A.16小时
B.小时
C.小时
D.17小时
答案:C
解析:解答:把点(1,4)分别代入y=kt,中,得k=4,m=4,
∴y=4t,,
把y=0.25代入y=4t中,得,
把y=0.25代入中,得,
∴治疗疾病有效的时间为:;
故选:C.
分析:将点(1,4)分别代入y=kt,中,求k、m,确定函数关系式,再把y=0.25代入两个函数式中求t,把所求两个时间t作差即可.灵活掌握反比例函数的图象性质的应用.
5.一个菱形的面积是4,则这个菱形的两条对角线长y与x的函数关系的图象大致是( )A.
B.
C.
D.
答案:C
解析:解答:根据菱形的面积公式:xy÷2=4,解得,y是x的反比例函数,x>0,y>0,
∴反比例函数的图象在第一象限.
故选:C.
分析:菱形的面积=对角线乘积的一半,列出关系式,写出y与x的函数关系式,根据变量的取值,确定函数所在的象限就可以确定函数的图象.
题型:单选题
6.矩形面积为4,它的一边长y与邻边长x的函数关系用图象表示大致是( )
A.
B.
C.
D.
答案:A
解析:解答:∵xy=4
∴(x>0,y>0)
故选:A.
分析:根据题意有:xy=4;故y与x之间的函数图象为反比例函数,且根据x、y实际意义x、y应大于0;从而得出答案.本题考查了反比例函数(k≠0)的图象与性质的应用.
7.蓄电池的电压为定值,使用此电源时,电流I(A)是电阻R(Ω)的反比例函数,其图象如图所示,当R为10Ω时,电流I是( )
A.3A
B.3.6A
C.4A
D.6A
答案:B
解析:解答:∵电流I(A)是电阻R(Ω)的反比例函数
∴设(k≠0)
把(4,9)代入得:k=4×9=36
∴
当R=10时,
I=36÷10=3.6A,
故选:B.
分析:根据电流I(A)是电阻R(Ω)的反比例函数,首先设出(k≠0),然后把(4,9)代入求出k的值,最后代入R=10求得I.
8.如图,一次函数y=-2x+b的图象与反比例函数的图象交于点A(1,6)、B(3,2)两点.b的值为( )
A.5
B.6
C.7
D.8
答案:D
解析:解答:把A(1,6)代入y=-2x+b得,
-2+b=6,
∴b=8;
故选:D.
分析:把A(1,6)代入y=-2x+b即可求得b的值;易错点是利用反例函数解析式求出k的值,错选B.
9.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V()的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
A.不小于
B.小于
C.不小于
D.小于
答案:C
解析:解答:设球内气体的气压P(kPa)和气体体积V()的关系式为,
∵图象过点(1.6,60)
∴k=96
即
在第一象限内,P随V的增大而减小,
∴当P≤120时,≥.
故选:C.
分析:根据题意可知温度不变时,气球内气体的气压P(kPa)是气体体积V()的反比例函数,且过点(1.6,60)所以P V=96;故当P≤120时,可以判断V不小于.根据图象上的已知点的坐标和实际问题,利用待定系数法求出函数解析式是解题的关键.
10.为了预防“HINI”流感,某校对教室进行药熏消毒,药品燃烧时,室内每立方米的含药量与时间成正比;燃烧后,室内每立方米含药量与时间成反比,则消毒过程中室内每立方米含药量y与时间t的函数关系图象大致为( )
A.
B.
C.
D.
答案:A
解析:解答:由正比例函数和反比例函数的图象性质,可判断:消毒过程中室内每立方米含药量y与时间t的函数关系图象大致为A.
故选:A.
分析:主要利用正比例函数和反比例函数的图象性质解答.正比例函数的图象是一条直线,反比例函数的图象是双曲线.
11.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( )
A.
B.
C.
D.
答案:A
解析:解答:∵是剪去的两个矩形,两个矩形的面积和为20,
∴xy=10,
∴y是x的反比例函数,
∵2≤x≤10,
∴答案为A.
故选:A.
分析:先根据图形的剪切确定变化过程中的函数关系式,确定函数类型,再根据自变量及函数的取值范围确定函数的具体图象.现实生活中存在大量成反比例函数的两个变量,确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限是解答该类问题的关键.
12.如图,反比例函数的一个分支与⊙O有两个交点A,B,且这个分支平分⊙O,以下说法正确的是( )
A.反比例函数的这个分支必过圆心O
B.劣弧AB等于120度
C.反比例函数的这个分支把⊙O的面积平分
D.反比例函数的这个分支把⊙O的周长平分
答案:D
解析:解答:A.反比例函数的这个分支不可能过圆心O,否则无法平分圆,所以错误;
B.劣弧AB等于180°,所以错误;
C.反比例函数的这个分支不能把⊙O的面积平分,所以错误;
D.这个分支平分⊙O,即反比例函数的这个分支把⊙O的周长平分,D正确.
故选:D.
分析:根据题意:这个分支平分⊙O,即反比例函数的这个分支把⊙O的周长平分可判断D正误.C一定错误,B中,根据劣弧AB等于180度判断.A中根据反比例函数的这个分支不可能过圆心O,否则无法平分圆,由此判断.本题考查反比例函数性质的运用,分别讨论判断正误.
13.一个圆锥的侧面展开图是一个面积为4平方单位的扇形,那么这个圆锥的母线长l与底面半径x之间的函数关系用图象表示大致是( )
A.
B.
C.
D.
答案:C
解析:解答:因为扇形面积为
,可得.
故选:C.
分析:先利用扇形的面积公式计算,再转化出圆锥的母线长l与底面半径x之间的函数关系.此题的关键是从扇形面积公式,转化出圆锥的母线长l与底面半径x之间的函数关系.熟悉反比例函数的图象也很关键.
14.如图,在直角坐标系中,有菱形OABC,A点的坐标是(10,0),双曲线(x>0)经过点C,且OB AC=160,则k的值为( )
A.40
B.48
C.64
D.80
答案:B
解析:解答:∵四边形OABC是菱形,OB与AC为两条对角线,且OB AC=160,
∴菱形OABC的面积为80,即OA CD=80,
∵OA=AC=10,
∴CD=8,
在Rt△OCD中,OC=10,CD=8,
根据勾股定理得:OD=6,即C(6,8),
则k的值为48.
故选:B.
分析:过C作CD垂直于x轴,交x轴于点D,由菱形的面积等于对角线乘积的一半,根据已知OB与AC的乘积求出菱形OABC的面积,而菱形的面积可以由OA乘以CD来求,根据OA的长求出CD的长,在直角三角形OCD中,利用勾股定理求出OD的长,确定出C的坐标,代入反比例解析式中可求出k的值.此题属于反比例函数综合题,涉及的知识有:菱形的性质,勾股定理,以及坐标与图形性质,求出C的坐标是解答本题的关键.
15.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:20
B.7:30
C.7:45
D.7:50
答案:A
解析:解答:∵开机加热时每分钟上升10℃,
∴从30℃到100℃需要7分钟,
设一次函数关系式为:y=k1x+b,
将(0,30),(7,100)代入y=k1x+b得k1=10,b=30
∴y=10x+30(0≤x≤7),令y=50,解得x=2;
设反比例函数关系式为:,
将(7,100)代入得k=700,
∴,
将y=30代入,解得;
∴(7≤x≤),令y=50,解得x=14.
所以,饮水机的一个循环周期为分钟.每一个循环周期内,在0≤x≤2及14≤x≤时间段内,水温不超过50℃.
逐一分析如下:
选项A:7:20至8:45之间有85分钟.85-×3=15,位于14≤x≤时间段内,故可行;
选项B:7:30至8:45之间有75分钟.75-×3=5,不在0≤x≤2及14≤x≤时间段内,故不可行;
选项C:7:45至8:45之间有60分钟.60-×2=≈13.3,不在0≤x≤2及14≤x≤时间段内,故不可行;
选项D:7:50至8:45之间有55分钟.55-×2=≈8.3,不在0≤x≤2及14≤x≤时间段内,故不可行.
综上所述,四个选项中,唯有7:20符合题意.
故选:A.
分析:第1步:求出两个函数的解析式;第2步:求出饮水机完成一个循环周期所需要的时间;第3步:求出每一个循环周期内,水温不超过50℃的时间段;第4步:结合4个选择项,逐一进行分析计算,得出结论.此题主要考查了一次函数及反比例函数的应用题,还有时间的讨论问题.关键要认真审题,理解题意.
二、填空题
16.你吃过兰州拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度ycm是面条粗细(横截面积)xcm2的反比例函数.假设它的图象如图所示,则y与x的函数表达式为______ .
答案:(x>0)
解析:解答:设反比例函数图象的解析式为,
由图可得,反比例函数上一点坐标为(0.04,3200)代入,有k=0.04×3200=128,
又题中实际意义需x>0.
∴(x>0).
故答案为:(x>0).
分析:根据反比例函数图象,设解析式为,由于点(0.04,3200)在图象上,代入反比例函数求得k的值.
17.一种新型汽车可装汽油500L,若汽车每小时用油量为xL.
①用油时间yh与每小时的用油量xL之间的函数表达式可表示为______;
答案:
②每小时的用油量为25L,则这些油可用的时间为______;
答案:20
③如果要使汽车连续行驶50h不需加油,那么每小时用油量的取值范围是______.
答案:0≤x<10
解析:解答:①∵可装汽油500L,若汽车每小时用油量为xL,
∴用油时间yh与每小时的用油量xL之间的函数表达式可表示为;
②每小时的用油量为25L,则这些油可用的时间为500÷25=20小时;
③如果要使汽车连续行驶50h不需加油,那么每小时用油量的取值范围0≤x<10;
故答案为:;20;0≤x<10;
分析:用总量除以每小时的用油量即可列出算式,代入有关数据求解即可.由反比例函数的图象的性质,进行解答.
18.小强欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为1000牛顿和0.5米,则当动力臂为1米时,撬动石头至少需要的力为 牛顿.
答案:500
解析:解答:由杠杆平衡条件可知:
=,
即:×1m=1000N×0.5m,
=500N
答案为:500.
分析:根据杠杆平衡条件=,代入有关数据即可.
19.如图,在平面直角坐标系中,在x轴上代表初始值x的那个点沿着竖线走,直到和曲线(x>0)交于点P后,在交点P处沿着东南方向(南偏东45°)走,一直和x轴相交,这个交点称投影点T.当x=1时,有P(1,4),相应的投影点T的坐标是(5,0);当x=2时,有P(2,2),相应的投影点T的坐标是(4,0);若投影点T的坐标是(,0)时,初始值x= .
答案:19
解析:解答:∵当x=1时,有P(1,4),相应的投影点T的坐标是(5,0);当x=2时,有P(2,2),相应的投影点T的坐标是(4,0);
∴1+4=5,2+2=4,
∴若投影点T的坐标是(,0)时,即x+=,
解得:x=19.
故答案为:19.
分析:根据已知数据得出投影点与P点坐标的关系,从而得出答案.
20.已知一定质量的二氧化碳的密度ρ(kg/)与体积V()成反比例函数关系,且当V=3.3时,ρ=3kg/;若要求二氧化碳的密度不超过1.5kg/,则体积V的变化范围是
答案:0≤v≤6.6
解析:解答:设二氧化碳的密度ρ(kg/)与体积V()之间的函数关系为,
∵当V=3.3时,ρ=3kg/;
∴m=ρV=3.3×3=9.9kg,
∴,
当ρ=1.5kg/时,
=6.6
故答案为:0≤v≤6.6.
分析:首先求出ρ与体积V之间的函数关系,然后根据密度的值确定体积的变化范围.
三、解答题
21.某商场出售一批名牌衬衣,衬衣进价为80元,在营销中发现,该衬衣的日销售量y(件)是日销售价x(元)的反比例函数,且当售价定为100元/件时,每日可售出30件.
(1)请求出y与x之间的函数关系式.
答案:
(2)若商场计划经营此种衬衣的日销售利润为2000元,则其单价应定为多少元?
答案:240
解析:解答:(1)设函数式为(k≠0).
,
k=3000
.
(2)单价是x元,
y(x-80)=2000
(x-80)=2000,
解得:x=240,
故单价定为 240元.
分析:(1)因为y与x成反比例函数关系,可设出函数式(k≠0),然后根据当售价定为100元/件时,每天可售出30件可求出k的值;(2)设单价是x元,根据每天可售出y件,每件的利润是(x-80)元,总利润为2000元,根据利润=售价-进价可列方程求解.
22.学校锅炉旁建有一个储煤库,开学初购进一批煤,现在知道:按每天用煤0.6吨计算,一学期(按150天计算)刚好用完.若每天的耗煤量为x吨,那么这批煤能维持y天.
(1)则y与x之间有怎样的函数关系?
答案:
(2)若每天节约0.1吨,则这批煤能维持多少天?
答案:180
解析:解答:(1)煤的总量为:0.6×150=90吨,
∵x y=90
∴;
(2)∵每天节约0.1吨煤,
∴每天的用煤量为0.6-0.1=0.5吨,
∴=180(天),
∴这批煤能维持180天.
分析:(1)首先求得煤的总量,然后利用耗煤量乘以天数等于煤总量得出函数关系式;(2)将每天的用煤量代入求得的函数解析式得到答案.
23.某汽车油箱的容积为70升,小王把油箱注满油后准备驾驶汽车从县城到300千米外的省城接待客人,在接到客人后立即按原路返回,请回答下列问题:
(1)油箱注满油后,汽车能够行使的总路程y(单位:千米)与平均耗油量x(单位:升/千米)之间有怎样的函数关系?
答案:(x>0)
(2)如果小王以平均每千米耗油0.1升的速度驾驶汽车到达省城,在返程时由于下雨,小王降低了车速,此时每行驶1千米的耗油量增加了一倍,如果小王一直以此速度行驶,邮箱里的油是否够回到县城?如果不够用,至少还需加多少油?
答案:不够用|20升
解析:解答:(1)∵耗油量×行驶里程=70升;
∴xy=70
∴(x>0);
(2)不够用,理由如下:
∵0.1×300=30(升) 0.2×300=60(升),
∴30+60>70 故不够用
30+60-70=20(升)
答:不够用,到县城至少还需加20升油.
分析:(1)根据耗油量×行驶里程=70升列出函数关系式即可;(2)分别求得每千米好友0.1升的速度的耗油量和0.2升的耗油量,与70比较即可得到答案.正确确定函数解析式是解题的关键.
24.如图是某电脑公司2011年的销售额y(万元)关于时间x(月)之间的函数图象,其中前几个月两变量之间满足反比例函数关系,后几个月两变量之间满足一次函数关系,观察图象,回答下列问题:
(1)该年度______月份的销售额最低;
答案:5
(2)求出该年度最低的销售额;
答案:5万元
(3)若电脑公司月销售额不大于10万元,则称销售处于淡季.在2011年中,该电脑公司哪几个月销售处于淡季?
答案:3月、4月、5月和6月这四个月
解析:解答:(1)观察函数图象知:5月份的销售额最低;
(2)当1≤x≤5时,设反比例函数的解析式为,
由题意得反比例函数的图象经过点(1,25)
∴
解得:k=25,
∴反比例函数的解析式为,
当x=5时,(万元)
答:该年度最低的销售额为5万元.
(3)当1≤x≤5时,若y≤10时,有≤10
∴x≥2.5
当5≤x≤12时,设函数解析式为y=kx+b
由题意得:
∴一次函数的解析式为y=5x-20
当5≤x≤12时,若y≤10,得:x≤6
∴当2.5≤x≤6的整数时,销售处于淡季.
即在2011年3月、4月、5月和6月这四个月,该电脑公司销售处于淡季.
分析:(1)直接观察图象即可得到答案;(2)求得反比例函数的解析式后即可求得5月份的最低销售额;(3)求得一次函数的解析式后利用自变量的取值范围确定答案即可.此题考查了反比例函数图象的性质、待定系数法求反比例函数解析式以及反比例函数图象上点的坐标特征.
25.心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第5分钟时与第30分钟时相比较,何时学生的注意力更集中?
答案:第30分钟
(2)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
答案:能
解析:解答:(1)设线段AB所在的直线的解析式为,
把B(10,40)代入得,=2,
∴.
设C、D所在双曲线的解析式为,
把C(25,40)代入得,=1000,
∴
当=5时,=2×5+20=30,
当=30时,,
∴<
∴第30分钟注意力更集中.
(2)令=36,
∴36=2x+20,
∴=8
令=36,
∴,
∴≈27.8
∵27.8-8=19.8>19,
∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
分析:(1)先用代定系数法分别求出AB和CD的函数表达式,再分别求第五分钟和第三十分钟的注意力指数,最后比较判断;(2)分别求出注意力指数为36时的两个时间,再将两时间之差和19比较,大于19则能讲完,否则不能.主要考查了函数的应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式,再根据自变量的值求算对应的函数值.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
