江苏省南京市溧水区东庐初级中学数学(苏科版)八年级下册导学案:9 中心对称图形复习(含解析)
文档属性
| 名称 | 江苏省南京市溧水区东庐初级中学数学(苏科版)八年级下册导学案:9 中心对称图形复习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 69.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-11 10:31:08 | ||
图片预览


文档简介
课题:中心对称图形复习
执笔:王静 审核:桑传生 课型:复习 时间:16年2月 日
学习目标:
1.回顾、思考本章所学的知识及思想方法,并对所学知识进行梳理,使所学知识系统化.
2.知道平行四边形与特殊平行四边形之间的 ( http: / / www.21cnjy.com )关系;进一步丰富对平面图形相关知识的认识,能有条理地、清晰地阐明自己的观点,培养学生归纳、反思的意识.
一、基础与巩固:
1.下列图形中,是中心对称图形而不是轴对称图形的是 ( )
A.平行四边形 B.矩形 C.菱形 D.正方形
【答案】A
2.平行四边形的对角线长为x、y,一边长为12,则x、y的值可能是( )
A.8和14 B.10和14 C.18和20 D. 10和34
【答案】C
3.在矩形ABCD中,AB=2AD,E是CD上一点,且AE=AB,则∠CBE=
【答案】45°
4.菱形的周长为16cm,两邻角的比为1∶2,则菱形的面积为 ㎝;
该菱形的高为 .
【答案】;
5.若矩形的一个角的平分线分一边为4cm和3cm的两部分,
则矩形的周长为__________.
【答案】22cm或20cm
6.正方形具有而菱形不一定具有的性质是 ( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.对角线平分一组对角
【答案】C
7.三角形三条中位线的长为3、4、5,则此三角形的面积为( )
A.12 B.24 C.36 D.48
【答案】B
8.在□ABCD中,对角线AC和BD相交于点O.
(1)如果∠ABO+∠ADO=90°,那么□ABCD是 形
(2)如果∠AOB=∠AOD,那么□ABCD是 形
(3)如果AB=BC,AC=BD,那么□ABCD是 形
【答案】矩;菱;正方
9.梯形的高是4,面积是32,上底长为4,则梯形的中位线长为 ,下底长为 .
【答案】8,12
10.如图:延长正方形ABCD的边BC至E,使CE=AC,连接AE交CD于F,
则∠AFC=___________.
( http: / / www.21cnjy.com )
【答案】112.5°
二、探究活动:
(一)、独立思考·解决问题
已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形BCD,把△ABD绕点D按顺时针方向旋转60°后得到△ECD.若AB=3,AC=2,
求∠BAD的度数与AD的长.
( http: / / www.21cnjy.com )
【答案】
( http: / / www.21cnjy.com )
练一练:
1.已知:如图,菱形ABCD的周长为20cm,2∠DAB=∠ABC,求对角线BD和AC的长.
( http: / / www.21cnjy.com )
【答案】
∵菱形ABCD的周长为20cm,
∴菱形的边长为20÷4=5(cm),
∵∠DAB:∠ABC=1:2,
∴∠DAB=
∴△ABD是等边三角形,
∴AB=DB=5cm.
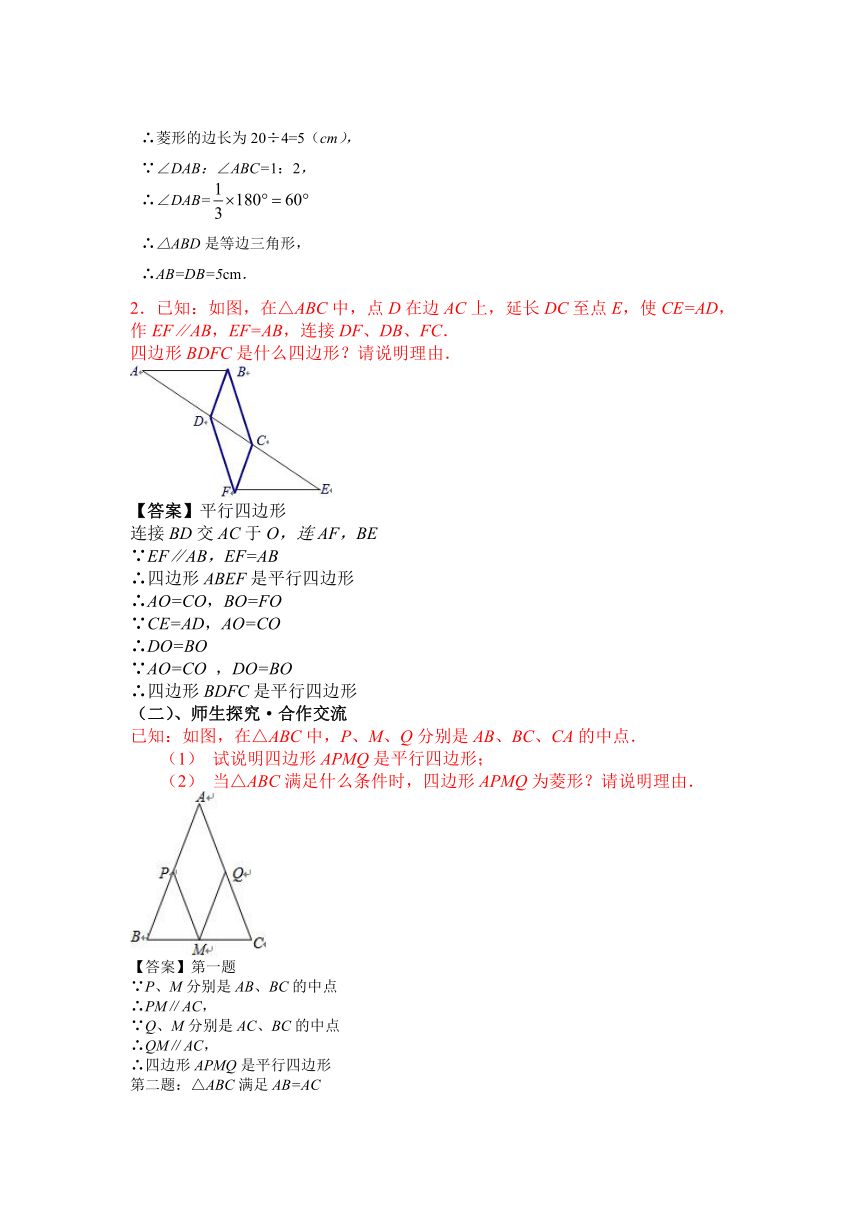
2.已知:如图,在△ABC中,点D在边AC上,延长DC至点E,使CE=AD,作EF∥AB,EF=AB,连接DF、DB、FC.
四边形BDFC是什么四边形?请说明理由.
( http: / / www.21cnjy.com )
【答案】平行四边形
连接BD交AC于O,连AF,BE
∵EF∥AB,EF=AB
∴四边形ABEF是平行四边形
∴AO=CO,BO=FO
∵CE=AD,AO=CO
∴DO=BO
∵AO=CO ,DO=BO
∴四边形BDFC是平行四边形
(二)、师生探究·合作交流
已知:如图,在△ABC中,P、M、Q分别是AB、BC、CA的中点.
试说明四边形APMQ是平行四边形;
当△ABC满足什么条件时,四边形APMQ为菱形?请说明理由.
( http: / / www.21cnjy.com )
【答案】第一题
∵P、M分别是AB、BC的中点
∴PM∥AC,
∵Q、M分别是AC、BC的中点
∴QM∥AC,
∴四边形APMQ是平行四边形
第二题:△ABC满足AB=AC
∵P、Q分别是AB、CA的中点
∴AP=AB,AQ=AC
∴AP =AQ
又∵四边形APMQ是平行四边形
∴四边形APMQ为菱形
做一做:
如图,△ABC中,∠C=90°, ∠A=45°,AB=6,点P在AB上,
PD⊥AC,PE⊥BC,垂足分别为D、E.
判断四边形PECD的形状,并说明理由;
当P在AB上运动时,四边形PECD有没有可能成为正方形?如有可能请指出点P的位置,如不可能请说明理由;
(3)当P在AB上运动时,四边形PECD的周长是否发生变化?如发生变化请说明理由,如不发生变化,请求出四边形PECD的周长.
( http: / / www.21cnjy.com )
【答案】第一题:矩形
∵PD⊥AC,PE⊥BC
∴∠DPE=90° ∠CEP=90°
∴∠DPE=∠CEP=∠C=90°
∴四边形PECD是矩形
第二题:可能,P为AB的中点
第三题:不会变化
由第一题已经证明四边形PECD是矩形
∴PD=CE,PE=CD
∵∠C=90°, ∠A=45°
∴∠B=180°—∠A—∠C=45°
∵∠CEP=90°,∠B=45°
∴∠EPB=180°—∠CEP—∠B =45°
∴∠EPB=∠B= 45°
∴PE=EB
∴四边形PECD的周长=2(PE+PD)=2(EB+CE)=2 BC
三、学习体会:
1.本节课你有哪些收获?你还有哪些疑惑?
2.你认为老师上课过程中还有哪些须要注意或改进的地方?
3.预习时的疑难解决了吗?
四、自我测试:
1.如图:在□ABCD中,AE⊥BC于E,AF⊥CD于F.若AE=4,
AF=6,且□ABCD的周长为40,则四边形ABCD的面积为( )
A.24 B.36 C.40 D.48
( http: / / www.21cnjy.com )
【答案】D
2.顺次连接四边形四边中点所组成的四边形是菱形,则原四边形为 ( )
A.平行四边形 B.菱形
C.对角线相等的四边形 D.直角梯形
【答案】C
3.平行四边形ABCD的周长为2a,两条对角线相交于O,△AOB的周长比△BOC的周长大b,则AB的长为 ( )
A. B. C. D.
【答案】B
4.菱形的周长为20cm,两邻角的比为1:2,则较长的对角线长为( )
A.4.5 cm B.4 cm C.5 cm D.4 cm
【答案】C
5.在四边形ABCD中,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD中任选两个使四边形ABCD为平行四边形的选法有 ( )
A.3 B.4 C.5 D.6
【答案】B
6.一个菱形的两条对角线长分别为6cm、8cm,则这个菱形的面积S为___________.
【答案】24
7.若矩形的一个角的平分线分一边为4cm和3cm的两部分,则矩形的周长为__________.
【答案】20cm或22
8.如图:点E、F分别是菱形ABCD的边BC、CD
上的点且∠EAF=∠D=60°,∠FAD=45°,则∠CFE=___________.
( http: / / www.21cnjy.com )
【答案】45°
9.如图:AE是正方形ABCD中∠BAC的平分线,AE分别交
BD、BC于F、E,AC、BD相交于O,求证:2OF=CE.
( http: / / www.21cnjy.com )
【答案】
( http: / / www.21cnjy.com )
执笔:王静 审核:桑传生 课型:复习 时间:16年2月 日
学习目标:
1.回顾、思考本章所学的知识及思想方法,并对所学知识进行梳理,使所学知识系统化.
2.知道平行四边形与特殊平行四边形之间的 ( http: / / www.21cnjy.com )关系;进一步丰富对平面图形相关知识的认识,能有条理地、清晰地阐明自己的观点,培养学生归纳、反思的意识.
一、基础与巩固:
1.下列图形中,是中心对称图形而不是轴对称图形的是 ( )
A.平行四边形 B.矩形 C.菱形 D.正方形
【答案】A
2.平行四边形的对角线长为x、y,一边长为12,则x、y的值可能是( )
A.8和14 B.10和14 C.18和20 D. 10和34
【答案】C
3.在矩形ABCD中,AB=2AD,E是CD上一点,且AE=AB,则∠CBE=
【答案】45°
4.菱形的周长为16cm,两邻角的比为1∶2,则菱形的面积为 ㎝;
该菱形的高为 .
【答案】;
5.若矩形的一个角的平分线分一边为4cm和3cm的两部分,
则矩形的周长为__________.
【答案】22cm或20cm
6.正方形具有而菱形不一定具有的性质是 ( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.对角线平分一组对角
【答案】C
7.三角形三条中位线的长为3、4、5,则此三角形的面积为( )
A.12 B.24 C.36 D.48
【答案】B
8.在□ABCD中,对角线AC和BD相交于点O.
(1)如果∠ABO+∠ADO=90°,那么□ABCD是 形
(2)如果∠AOB=∠AOD,那么□ABCD是 形
(3)如果AB=BC,AC=BD,那么□ABCD是 形
【答案】矩;菱;正方
9.梯形的高是4,面积是32,上底长为4,则梯形的中位线长为 ,下底长为 .
【答案】8,12
10.如图:延长正方形ABCD的边BC至E,使CE=AC,连接AE交CD于F,
则∠AFC=___________.
( http: / / www.21cnjy.com )
【答案】112.5°
二、探究活动:
(一)、独立思考·解决问题
已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形BCD,把△ABD绕点D按顺时针方向旋转60°后得到△ECD.若AB=3,AC=2,
求∠BAD的度数与AD的长.
( http: / / www.21cnjy.com )
【答案】
( http: / / www.21cnjy.com )
练一练:
1.已知:如图,菱形ABCD的周长为20cm,2∠DAB=∠ABC,求对角线BD和AC的长.
( http: / / www.21cnjy.com )
【答案】
∵菱形ABCD的周长为20cm,
∴菱形的边长为20÷4=5(cm),
∵∠DAB:∠ABC=1:2,
∴∠DAB=
∴△ABD是等边三角形,
∴AB=DB=5cm.
2.已知:如图,在△ABC中,点D在边AC上,延长DC至点E,使CE=AD,作EF∥AB,EF=AB,连接DF、DB、FC.
四边形BDFC是什么四边形?请说明理由.
( http: / / www.21cnjy.com )
【答案】平行四边形
连接BD交AC于O,连AF,BE
∵EF∥AB,EF=AB
∴四边形ABEF是平行四边形
∴AO=CO,BO=FO
∵CE=AD,AO=CO
∴DO=BO
∵AO=CO ,DO=BO
∴四边形BDFC是平行四边形
(二)、师生探究·合作交流
已知:如图,在△ABC中,P、M、Q分别是AB、BC、CA的中点.
试说明四边形APMQ是平行四边形;
当△ABC满足什么条件时,四边形APMQ为菱形?请说明理由.
( http: / / www.21cnjy.com )
【答案】第一题
∵P、M分别是AB、BC的中点
∴PM∥AC,
∵Q、M分别是AC、BC的中点
∴QM∥AC,
∴四边形APMQ是平行四边形
第二题:△ABC满足AB=AC
∵P、Q分别是AB、CA的中点
∴AP=AB,AQ=AC
∴AP =AQ
又∵四边形APMQ是平行四边形
∴四边形APMQ为菱形
做一做:
如图,△ABC中,∠C=90°, ∠A=45°,AB=6,点P在AB上,
PD⊥AC,PE⊥BC,垂足分别为D、E.
判断四边形PECD的形状,并说明理由;
当P在AB上运动时,四边形PECD有没有可能成为正方形?如有可能请指出点P的位置,如不可能请说明理由;
(3)当P在AB上运动时,四边形PECD的周长是否发生变化?如发生变化请说明理由,如不发生变化,请求出四边形PECD的周长.
( http: / / www.21cnjy.com )
【答案】第一题:矩形
∵PD⊥AC,PE⊥BC
∴∠DPE=90° ∠CEP=90°
∴∠DPE=∠CEP=∠C=90°
∴四边形PECD是矩形
第二题:可能,P为AB的中点
第三题:不会变化
由第一题已经证明四边形PECD是矩形
∴PD=CE,PE=CD
∵∠C=90°, ∠A=45°
∴∠B=180°—∠A—∠C=45°
∵∠CEP=90°,∠B=45°
∴∠EPB=180°—∠CEP—∠B =45°
∴∠EPB=∠B= 45°
∴PE=EB
∴四边形PECD的周长=2(PE+PD)=2(EB+CE)=2 BC
三、学习体会:
1.本节课你有哪些收获?你还有哪些疑惑?
2.你认为老师上课过程中还有哪些须要注意或改进的地方?
3.预习时的疑难解决了吗?
四、自我测试:
1.如图:在□ABCD中,AE⊥BC于E,AF⊥CD于F.若AE=4,
AF=6,且□ABCD的周长为40,则四边形ABCD的面积为( )
A.24 B.36 C.40 D.48
( http: / / www.21cnjy.com )
【答案】D
2.顺次连接四边形四边中点所组成的四边形是菱形,则原四边形为 ( )
A.平行四边形 B.菱形
C.对角线相等的四边形 D.直角梯形
【答案】C
3.平行四边形ABCD的周长为2a,两条对角线相交于O,△AOB的周长比△BOC的周长大b,则AB的长为 ( )
A. B. C. D.
【答案】B
4.菱形的周长为20cm,两邻角的比为1:2,则较长的对角线长为( )
A.4.5 cm B.4 cm C.5 cm D.4 cm
【答案】C
5.在四边形ABCD中,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD中任选两个使四边形ABCD为平行四边形的选法有 ( )
A.3 B.4 C.5 D.6
【答案】B
6.一个菱形的两条对角线长分别为6cm、8cm,则这个菱形的面积S为___________.
【答案】24
7.若矩形的一个角的平分线分一边为4cm和3cm的两部分,则矩形的周长为__________.
【答案】20cm或22
8.如图:点E、F分别是菱形ABCD的边BC、CD
上的点且∠EAF=∠D=60°,∠FAD=45°,则∠CFE=___________.
( http: / / www.21cnjy.com )
【答案】45°
9.如图:AE是正方形ABCD中∠BAC的平分线,AE分别交
BD、BC于F、E,AC、BD相交于O,求证:2OF=CE.
( http: / / www.21cnjy.com )
【答案】
( http: / / www.21cnjy.com )
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
