10.4平移 同步课件(共23张PPT) 2024-2025学年沪科版七年级数学下册
文档属性
| 名称 | 10.4平移 同步课件(共23张PPT) 2024-2025学年沪科版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
10.4 平移
第10章相交线、平行线与平移
沪科版数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
了解平移的概念及其性质.
能按要求作出简单的平面图形平移后的图形,能利用平移进行简单的图案设计.
经历操作、观察、分析等过程,探索认识平移的性质,进一步发展空间观念,增强审美意识.
(一)知识与技能目标
学生能准确识别相交线、平行线,理解对顶角、邻补角的概念,掌握对顶角相等、邻补角互补的性质。
理解垂线、垂线段的概念,掌握垂线的性质,会用三角尺或量角器过一点画已知直线的垂线,了解垂线段最短的性质,理解点到直线的距离的意义并能度量。
认识同位角、内错角、同旁内角,掌握平行线的判定方法和平行线的性质,能运用判定方法和性质进行简单的推理和计算。
了解平移的概念,理解平移的基本性质,能按要求作出简单平面图形平移后的图形,会利用平移进行图案设计。
(二)过程与方法目标
通过观察、操作、推理、交流等活动,进一步发展空间观念,培养学生的推理能力和有条理的表达能力。
经历探索相交线、平行线与平移的性质和判定过程,体会从具体到抽象、从特殊到一般的数学思想方法。
(三)情感态度与价值观目标
让学生在自主探究与合作交流中感受数学学习的乐趣,培养学生勇于探索、敢于创新的精神。
体会数学与生活的紧密联系,激发学生学习数学的兴趣,增强学生应用数学的意识。
二、教学重难点
(一)教学重点
对顶角、邻补角的性质,垂线的性质,平行线的判定方法和平行线的性质。
平移的性质以及利用平移设计图案。
(二)教学难点
区分平行线的判定方法和平行线的性质,能正确运用它们进行推理和计算。
理解平移的性质,特别是图形平移前后对应点连线平行且相等的性质,并能运用平移解决实际问题。
三、教学方法
讲授法:系统讲解相交线、平行线与平移的基本概念、性质和判定方法,构建清晰的知识框架。
讨论法:组织学生对一些几何问题进行讨论,如平行线判定方法的证明思路,促进学生思维碰撞,加深对知识的理解。
探究法:设置探究活动,如探究垂线的性质、平移的性质等,引导学生自主探索,培养学生的自主学习能力。
直观演示法:利用多媒体、教具等直观手段,展示相交线、平行线和平移的动态过程,帮助学生理解抽象的几何概念。
练习法:通过针对性的练习题,巩固学生所学知识,提高学生解题能力和应用能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
一般地,在平面内,将一个图形按某一方向移动一定的距离,这样的图形运动叫作平移.
图形平移的方向不限于水平或竖直方向,图形可以沿平面内任何方向平移.
问题1:如何在一张半透明的纸上,画出一排形状和大小如图的尼克呢?
思考:“尼克”的形状、大小、位置在运动前后是否发生了变化?
形状不变,大小不变,位置改变
知识点一 平移的相关概念
平移在我们日常生活中是很常见的,你能举出生活中一些利用平移的例子吗?
抽屉的推拉.
行驶在笔直公路上的汽车.
传送带上的行李.
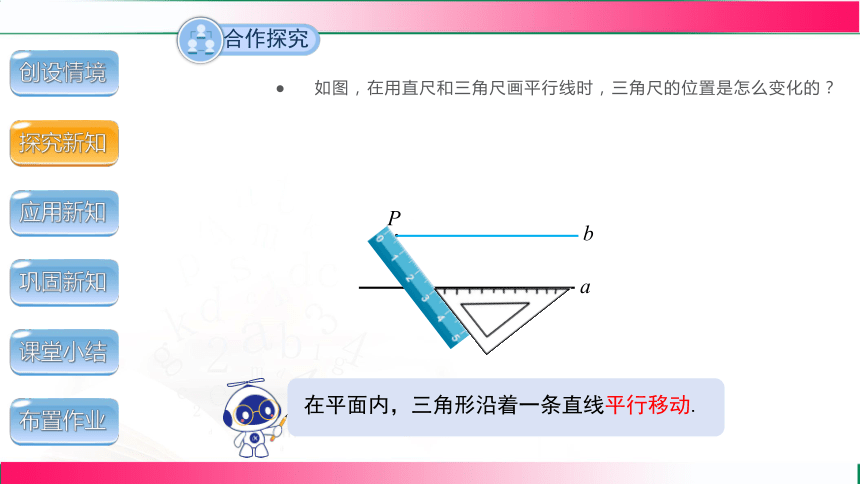
如图,在用直尺和三角尺画平行线时,三角尺的位置是怎么变化的?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
合作探究
P
a
.
b
在平面内,三角形沿着一条直线平行移动.
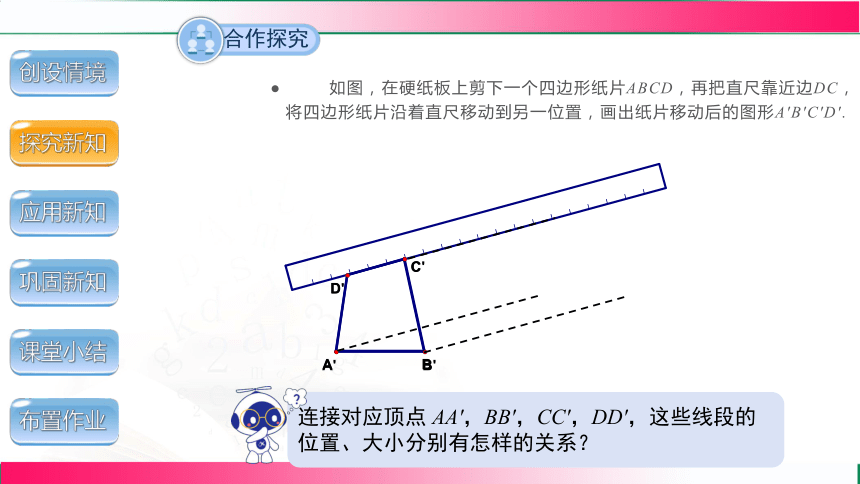
如图,在硬纸板上剪下一个四边形纸片ABCD,再把直尺靠近边DC,将四边形纸片沿着直尺移动到另一位置,画出纸片移动后的图形A'B'C'D'.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
合作探究
连接对应顶点 AA',BB',CC',DD',这些线段的位置、大小分别有怎样的关系?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
合作探究
位置
AA'//BB'//CC''//DD'
长短
AA'=BB'=CC'=DD'
观察可得:
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
在平面内,一个图形整体沿某个方向移动一定的距离,这种图形的变化叫做平移.
平移时,原图形上的一点 A 平移后成为点 A',这样的两点叫做对应点.
平移的性质:
平移前后,连接对应点的线段互相平行(或在同一条直线上)且相等.
平移只改变图形的位置,不改变图形的形状和大小.
归纳
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
例1 如图,平移△ABC,使点A移动到点A',画出平移后的△A'B'C'.
A
B
C
A'
B'
C'
连接A'A;过点B,作 l∥AA',在l上截取BB' =AA'
同理作CC',连接A'B' ,B'C',C'A'则△A'B'C'即为所求.
l
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
例2 如图,在△ ABC中,∠C=90°,∠ABC=30°,AB=4,将
△ ABC 沿射线PQ的方向平移5个单位长度后得到△ A′B′C′.
(1)A′B′的长为_______;∠B′A′C′的度数为_______;
(2)A′A 与B′B有什么关系?
(3)四边形ABB′A′的周长为_______.
4
60°
平行且相等
18
知识点1 平移的定义
1. 在下列生活现象中,不是平移的是( )
A
A. 小亮荡秋千的运动 B. 拉开抽屉的运动
C. 电梯的运行过程 D. 列车的直线行驶过程
2. [2024芜湖无为市期中] 将图中的小兔进行平移
后,得到的图案是( )
C
A. B. C. D.
返回
知识点2 平移的性质
(第3题)
3. 如图,将三角形沿 向右平移得到
三角形,若,,则 的长是
( )
A
A. 2 B. 2.5 C. 3 D. 5
返回
(第4题)
4. [2024马鞍山八中期末] 如图,将三角形
平移到三角形 的位置,则下列说法:
;; ;
④平移距离为线段 的长.
其中说法正确的有( )
D
A. ①② B. ②③ C. ①③ D. ②④
返回
5.如图,三角形的边长为,将三角形 平移
得到三角形,且 ,则阴影部分的面积为
___ .
8
返回
6.如图,在三角形 中,
, ,
,将三角形沿 方向
向右平移得到三角形 ,若
, .
(1) 的长为______;
【点拨】因为三角形沿方向向右平移得到三角形 ,
所以.因为, ,所以
.
(2)求四边形 的周长.
【解】因为三角形沿方向向右平移得到三角形 ,
所以,,所以四边形
的周长为
返回
知识点3 平移作图
7.[2024亳州期末] 如图,在 的正方
形网格中,每个小正方形的边长均为1个
单位,三角形 的顶点均在网格的格点
上(小正方形的顶点即为格点).
(1)将三角形 先向左平移1个单位,再向上平移3个单位,
点,,的对应点分别为,, ,请在网格图中画出
平移后的三角形;
【解】如图所示,三角形
即为所求.
(2)求三角形 的面积.
【解】三角形的面积为 .
返回
布置作业
创设情境
探究新知
探究新知
应用新知
巩固新知
课堂小结
平移:
在平面内,一个图形整体沿某个方向移动一定的距离,这种图形的变化叫做平移.
平移时,原图形上的一点 A 平移后成为点 A',这样的两点叫做对应点.
平移
平移的性质:
平移前后,连接对应点的线段互相平行(或在同一条直线上)且相等.
平移只改变图形的位置,不改变图形的形状和大小.
创设情境
探究新知
探究新知
应用新知
巩固新知
布置作业
课堂小结
完成教材上的课后习题
谢谢观看!
10.4 平移
第10章相交线、平行线与平移
沪科版数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
了解平移的概念及其性质.
能按要求作出简单的平面图形平移后的图形,能利用平移进行简单的图案设计.
经历操作、观察、分析等过程,探索认识平移的性质,进一步发展空间观念,增强审美意识.
(一)知识与技能目标
学生能准确识别相交线、平行线,理解对顶角、邻补角的概念,掌握对顶角相等、邻补角互补的性质。
理解垂线、垂线段的概念,掌握垂线的性质,会用三角尺或量角器过一点画已知直线的垂线,了解垂线段最短的性质,理解点到直线的距离的意义并能度量。
认识同位角、内错角、同旁内角,掌握平行线的判定方法和平行线的性质,能运用判定方法和性质进行简单的推理和计算。
了解平移的概念,理解平移的基本性质,能按要求作出简单平面图形平移后的图形,会利用平移进行图案设计。
(二)过程与方法目标
通过观察、操作、推理、交流等活动,进一步发展空间观念,培养学生的推理能力和有条理的表达能力。
经历探索相交线、平行线与平移的性质和判定过程,体会从具体到抽象、从特殊到一般的数学思想方法。
(三)情感态度与价值观目标
让学生在自主探究与合作交流中感受数学学习的乐趣,培养学生勇于探索、敢于创新的精神。
体会数学与生活的紧密联系,激发学生学习数学的兴趣,增强学生应用数学的意识。
二、教学重难点
(一)教学重点
对顶角、邻补角的性质,垂线的性质,平行线的判定方法和平行线的性质。
平移的性质以及利用平移设计图案。
(二)教学难点
区分平行线的判定方法和平行线的性质,能正确运用它们进行推理和计算。
理解平移的性质,特别是图形平移前后对应点连线平行且相等的性质,并能运用平移解决实际问题。
三、教学方法
讲授法:系统讲解相交线、平行线与平移的基本概念、性质和判定方法,构建清晰的知识框架。
讨论法:组织学生对一些几何问题进行讨论,如平行线判定方法的证明思路,促进学生思维碰撞,加深对知识的理解。
探究法:设置探究活动,如探究垂线的性质、平移的性质等,引导学生自主探索,培养学生的自主学习能力。
直观演示法:利用多媒体、教具等直观手段,展示相交线、平行线和平移的动态过程,帮助学生理解抽象的几何概念。
练习法:通过针对性的练习题,巩固学生所学知识,提高学生解题能力和应用能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
一般地,在平面内,将一个图形按某一方向移动一定的距离,这样的图形运动叫作平移.
图形平移的方向不限于水平或竖直方向,图形可以沿平面内任何方向平移.
问题1:如何在一张半透明的纸上,画出一排形状和大小如图的尼克呢?
思考:“尼克”的形状、大小、位置在运动前后是否发生了变化?
形状不变,大小不变,位置改变
知识点一 平移的相关概念
平移在我们日常生活中是很常见的,你能举出生活中一些利用平移的例子吗?
抽屉的推拉.
行驶在笔直公路上的汽车.
传送带上的行李.
如图,在用直尺和三角尺画平行线时,三角尺的位置是怎么变化的?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
合作探究
P
a
.
b
在平面内,三角形沿着一条直线平行移动.
如图,在硬纸板上剪下一个四边形纸片ABCD,再把直尺靠近边DC,将四边形纸片沿着直尺移动到另一位置,画出纸片移动后的图形A'B'C'D'.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
合作探究
连接对应顶点 AA',BB',CC',DD',这些线段的位置、大小分别有怎样的关系?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
合作探究
位置
AA'//BB'//CC''//DD'
长短
AA'=BB'=CC'=DD'
观察可得:
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
在平面内,一个图形整体沿某个方向移动一定的距离,这种图形的变化叫做平移.
平移时,原图形上的一点 A 平移后成为点 A',这样的两点叫做对应点.
平移的性质:
平移前后,连接对应点的线段互相平行(或在同一条直线上)且相等.
平移只改变图形的位置,不改变图形的形状和大小.
归纳
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
例1 如图,平移△ABC,使点A移动到点A',画出平移后的△A'B'C'.
A
B
C
A'
B'
C'
连接A'A;过点B,作 l∥AA',在l上截取BB' =AA'
同理作CC',连接A'B' ,B'C',C'A'则△A'B'C'即为所求.
l
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
例2 如图,在△ ABC中,∠C=90°,∠ABC=30°,AB=4,将
△ ABC 沿射线PQ的方向平移5个单位长度后得到△ A′B′C′.
(1)A′B′的长为_______;∠B′A′C′的度数为_______;
(2)A′A 与B′B有什么关系?
(3)四边形ABB′A′的周长为_______.
4
60°
平行且相等
18
知识点1 平移的定义
1. 在下列生活现象中,不是平移的是( )
A
A. 小亮荡秋千的运动 B. 拉开抽屉的运动
C. 电梯的运行过程 D. 列车的直线行驶过程
2. [2024芜湖无为市期中] 将图中的小兔进行平移
后,得到的图案是( )
C
A. B. C. D.
返回
知识点2 平移的性质
(第3题)
3. 如图,将三角形沿 向右平移得到
三角形,若,,则 的长是
( )
A
A. 2 B. 2.5 C. 3 D. 5
返回
(第4题)
4. [2024马鞍山八中期末] 如图,将三角形
平移到三角形 的位置,则下列说法:
;; ;
④平移距离为线段 的长.
其中说法正确的有( )
D
A. ①② B. ②③ C. ①③ D. ②④
返回
5.如图,三角形的边长为,将三角形 平移
得到三角形,且 ,则阴影部分的面积为
___ .
8
返回
6.如图,在三角形 中,
, ,
,将三角形沿 方向
向右平移得到三角形 ,若
, .
(1) 的长为______;
【点拨】因为三角形沿方向向右平移得到三角形 ,
所以.因为, ,所以
.
(2)求四边形 的周长.
【解】因为三角形沿方向向右平移得到三角形 ,
所以,,所以四边形
的周长为
返回
知识点3 平移作图
7.[2024亳州期末] 如图,在 的正方
形网格中,每个小正方形的边长均为1个
单位,三角形 的顶点均在网格的格点
上(小正方形的顶点即为格点).
(1)将三角形 先向左平移1个单位,再向上平移3个单位,
点,,的对应点分别为,, ,请在网格图中画出
平移后的三角形;
【解】如图所示,三角形
即为所求.
(2)求三角形 的面积.
【解】三角形的面积为 .
返回
布置作业
创设情境
探究新知
探究新知
应用新知
巩固新知
课堂小结
平移:
在平面内,一个图形整体沿某个方向移动一定的距离,这种图形的变化叫做平移.
平移时,原图形上的一点 A 平移后成为点 A',这样的两点叫做对应点.
平移
平移的性质:
平移前后,连接对应点的线段互相平行(或在同一条直线上)且相等.
平移只改变图形的位置,不改变图形的形状和大小.
创设情境
探究新知
探究新知
应用新知
巩固新知
布置作业
课堂小结
完成教材上的课后习题
谢谢观看!
