6.1 二元一次方程组和它的解 课件(共25张PPT)
文档属性
| 名称 | 6.1 二元一次方程组和它的解 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
6.1 二元一次方程组和它的解
第6章 一次方程组
华东师大版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.了解二元一次方程(组)及其解的定义.
2.会列二元一次方程组,并检验一组数是不是某个二元一次方程组的解.
3.能根据实际问题中的数量关系列出简单的二元一次方程(组).
我会从教学目标、教学重难点、教学方法等方面入手,为你撰写一份完整的教案。
# 一元一次方程教案
## 一、教学目标
1. 知识与技能目标
- 理解一元一次方程的概念,能准确识别一元一次方程。
- 掌握一元一次方程的解法,能熟练求解简单的一元一次方程。
2. 过程与方法目标
- 通过观察、分析、归纳等活动,培养学生的逻辑思维能力和抽象概括能力。
- 经历从实际问题中建立一元一次方程模型的过程,体会方程是解决实际问题的重要数学工具。
3. 情感态度与价值观目标
- 激发学生学习数学的兴趣,培养学生的合作交流意识和勇于探索的精神。
## 二、教学重难点
1. **重点**
- 一元一次方程的概念和方程的解的概念。
- 一元一次方程的解法,特别是移项法则的应用。
2. **难点**
- 从实际问题中抽象出一元一次方程模型,找出等量关系。
- 正确理解和运用移项法则解方程。
## 三、教学方法
讲授法、讨论法、练习法相结合
## 四、教学过程
1. **导入新课(5分钟)**
- 通过展示生活中的实际问题,如购物打折、行程问题等,引导学生思考如何用数学方法解决这些问题,从而引出方程的概念。
2. **讲授新课(25分钟)**
- 一元一次方程的概念
- 展示一些方程,让学生观察它们的特点,引导学生归纳出一元一次方程的定义:只含有一个未知数,并且未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。
- 方程的解的概念
- 给出一些方程,让学生尝试代入不同的值,看哪个值能使方程左右两边相等,从而引出方程的解的概念:使方程左右两边相等的未知数的值叫做方程的解。
- 一元一次方程的解法
- 以简单的一元一次方程为例,如2x + 3 = 7,讲解移项法则:把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项。通过移项将方程化为ax = b(a≠0)的形式,然后求解x = b/a。
3. **课堂练习(15分钟)**
- 给出一些一元一次方程,让学生进行练习,巩固所学的解法。教师巡视指导,及时纠正学生的错误。
4. **课堂小结(5分钟)**
- 与学生一起回顾本节课所学的内容,包括一元一次方程的概念、方程的解的概念以及一元一次方程的解法。
5. **布置作业(5分钟)**
- 布置适量的课后作业,让学生进一步巩固所学知识。
## 五、教学反思
在教学过程中,要注重引导学生积极参与课堂活动,通过实际问题的引入,激发学生的学习兴趣。在讲解一元一次方程的解法时,要注重步骤的规范性和逻辑性,让学生理解每一步的依据。同时,要关注学生的练习情况,及时反馈和纠正学生的错误,确保学生掌握一元一次方程的解法。
这份教案你觉得怎么样?如果你对教学过程中的某个环节还有更具体的要求,比如导入新课的实际问题、课堂练习的题目类型等,都可以告诉我。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
“我们的小世界杯”足球赛规定:胜一场得3分,平一场得1分,负一场得0分.勇士队赛了9场,共得17分.已知这个队负了2场,那么这个队胜了几场?平了几场呢?
设勇士队胜了x场,平了y场,可列出方程组:
这就要研究含有两个未知数的方程组了!
★本章将研究一次方程组的解法,并应用一次方程组解决一些实际问题,从中体会消元的思想方法.
什么叫一元一次方程 什么叫一元一次方程的解 怎样检验一个数
是否是这个方程的解
只含有一个未知数、左右两边都是整式,并且含未知数的项的次数都是1的方程叫做一元一次方程.
能使方程左、右两边的值相等的未知数的值,叫做方程的解.
问题1 暑假里,某地组织了“我们的小世界杯”足球邀请赛.比赛规定:胜一场得3分,平一场得1分,负一场得0分.勇士队在第一轮比赛中赛了9场,负了2场,共得17分.那么这个队胜了几场?平了几场呢?
知识点1 二元一次方程(组)的定义
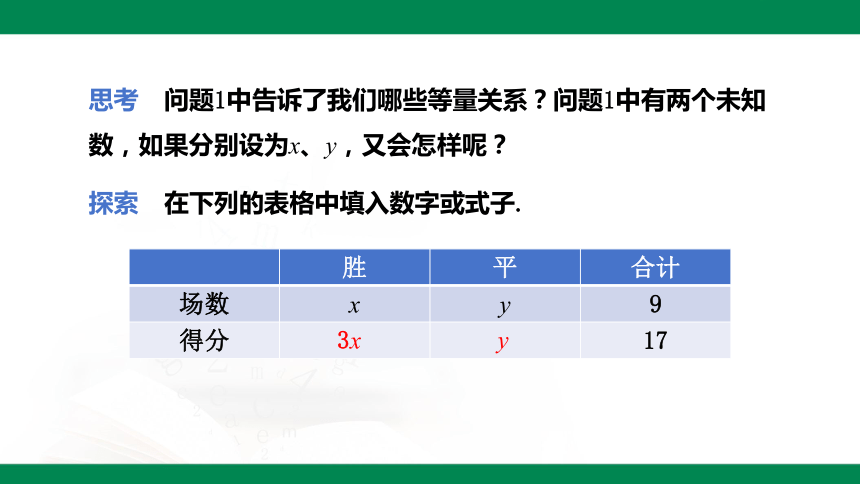
思考 问题1中告诉了我们哪些等量关系?问题1中有两个未知数,如果分别设为x、y,又会怎样呢?
探索 在下列的表格中填入数字或式子.
胜 平 合计
场数 x y 9
得分 17
3x
y
设勇士队胜了x场,平了y场,那么根据题意,得
x+y=9-2 ①
和
3x+y=17. ②
这两个方程
有什么共同
特点?
上面所列方程各含有几个未知数
含有未知数的项的次数是多少
答:2个未知数
答:次数是1
归纳 像这样,有两个未知数,并且含有未知数的项的次数都是1的方程,叫做二元一次方程.
这个问题中,两个未知量(比赛场数)要满足两个等量关系.相应地,两个未知数x、y必须同时满足①②两个方程.因此,把这两个方程合在一起,并写成
归纳 像这样,两个二元一次方程合在一起,就组成了一个二元一次方程组.
注意:方程组各方程中同一字母必须代表同一个量.
例如: x=5 , y=2 是方程x+y=7 的一个解,记作
x=5,
y=2
知识点2 二元一次方程(组)的解
使二元一次方程的左、右两边的值相等的一对未知数的值,叫做二元一次方程的解.
x=5 ,y =2是否为方程 x+y=7的一个解
x=5 , y =2是否为方程 3x +y=17的一个解
x+y=7,
3x+y=17
的解.
{
就是二元一次方程组
x=5
y=2
例如,
{
一般地,使二元一次方程组中两个方程的左、右两边的值都相等的一对未知数的值,叫做二元一次方程组的解.
知识点2 二元一次方程(组)的解
问题3 某校现有校舍20 000m ,计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%.若新建校舍的面积为被拆除的旧校舍面积的4倍,则应拆除多少旧校舍,建造多少新校舍?
知识点3 根据题意列二元一次方程(组)
试一试
若设应拆除x 旧校舍,建造y新校舍,请你根据题意列出方程组.
分析 根据条件可知,题中的等量关系为:
新建校舍的面积=被拆除的旧校舍面积的4倍;
新建校舍的面积-被拆除旧校舍的面积=现有校舍面积的30%.
根据此等量关系列出方程组,
(1)审题:仔细审题,弄清题目中的已知量与未知量及两者之间的联系;
(2)设未知数:弄清题意和题目中的数量关系,设出两个未知数,并用含未知数的代数式表示其他需要的量;
(3)找等量关系:通过阅读理解,找出两个等量关系;
(4)列方程组:根据等量关系,列出二元一次方程组.
根据实际问题列二元一次方程组的步骤:
1. [2024无锡期中] 下列方程组中,是二元一次方程组的是
( )
B
A. B.
C. D.
返回
2. 下列判断中,正确的是( )
D
A. 方程 不是二元一次方程
B. 任何一个二元一次方程都只有一个解
C. 方程有无数组解,任何一组, 的值都是该方
程的解
D. 既是方程的解也是方程 的解
返回
3. 下列各组数值中,是二元一次方程组
的解的是( )
B
A. B.
C. D.
返回
4.[2024沈阳期末] 现用95张纸板制作一批盒子,每张纸板可
做4个盒身或做11个盒底,而一个盒身和两个盒底配成一个
完整的盒子.问用多少张纸板制盒身、多少张纸板制盒底,可
以使盒身和盒底正好配套?设用张纸板做盒身, 张纸板做
盒底,可以使盒身与盒底正好配套,则可列方程是
_ _____________.
5.如果是关于, 的二元一次方程,
则 的值为____.
返回
6. 写出二元一次方程 的一组整数
解:_ _____________________.
7.已知是方程的解,则式子 的
值为___.
(答案不唯一)
1
【点拨】将代入,可得 ,则
.
返回
8. 已知方程组
(1)分别取, ,0,2,填写下表:
方程
0 2
___ ___ ____ ____
方程
0 2
_ _ ___ _ _ ___
8
2
2
4
(2)根据(1)中的数据写出方程组的解.
【解】方程组的解为
返回
二元一次方程组的定义
认识二元一次方程组
二元一次方程组的解
谢谢观看!
6.1 二元一次方程组和它的解
第6章 一次方程组
华东师大版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.了解二元一次方程(组)及其解的定义.
2.会列二元一次方程组,并检验一组数是不是某个二元一次方程组的解.
3.能根据实际问题中的数量关系列出简单的二元一次方程(组).
我会从教学目标、教学重难点、教学方法等方面入手,为你撰写一份完整的教案。
# 一元一次方程教案
## 一、教学目标
1. 知识与技能目标
- 理解一元一次方程的概念,能准确识别一元一次方程。
- 掌握一元一次方程的解法,能熟练求解简单的一元一次方程。
2. 过程与方法目标
- 通过观察、分析、归纳等活动,培养学生的逻辑思维能力和抽象概括能力。
- 经历从实际问题中建立一元一次方程模型的过程,体会方程是解决实际问题的重要数学工具。
3. 情感态度与价值观目标
- 激发学生学习数学的兴趣,培养学生的合作交流意识和勇于探索的精神。
## 二、教学重难点
1. **重点**
- 一元一次方程的概念和方程的解的概念。
- 一元一次方程的解法,特别是移项法则的应用。
2. **难点**
- 从实际问题中抽象出一元一次方程模型,找出等量关系。
- 正确理解和运用移项法则解方程。
## 三、教学方法
讲授法、讨论法、练习法相结合
## 四、教学过程
1. **导入新课(5分钟)**
- 通过展示生活中的实际问题,如购物打折、行程问题等,引导学生思考如何用数学方法解决这些问题,从而引出方程的概念。
2. **讲授新课(25分钟)**
- 一元一次方程的概念
- 展示一些方程,让学生观察它们的特点,引导学生归纳出一元一次方程的定义:只含有一个未知数,并且未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。
- 方程的解的概念
- 给出一些方程,让学生尝试代入不同的值,看哪个值能使方程左右两边相等,从而引出方程的解的概念:使方程左右两边相等的未知数的值叫做方程的解。
- 一元一次方程的解法
- 以简单的一元一次方程为例,如2x + 3 = 7,讲解移项法则:把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项。通过移项将方程化为ax = b(a≠0)的形式,然后求解x = b/a。
3. **课堂练习(15分钟)**
- 给出一些一元一次方程,让学生进行练习,巩固所学的解法。教师巡视指导,及时纠正学生的错误。
4. **课堂小结(5分钟)**
- 与学生一起回顾本节课所学的内容,包括一元一次方程的概念、方程的解的概念以及一元一次方程的解法。
5. **布置作业(5分钟)**
- 布置适量的课后作业,让学生进一步巩固所学知识。
## 五、教学反思
在教学过程中,要注重引导学生积极参与课堂活动,通过实际问题的引入,激发学生的学习兴趣。在讲解一元一次方程的解法时,要注重步骤的规范性和逻辑性,让学生理解每一步的依据。同时,要关注学生的练习情况,及时反馈和纠正学生的错误,确保学生掌握一元一次方程的解法。
这份教案你觉得怎么样?如果你对教学过程中的某个环节还有更具体的要求,比如导入新课的实际问题、课堂练习的题目类型等,都可以告诉我。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
“我们的小世界杯”足球赛规定:胜一场得3分,平一场得1分,负一场得0分.勇士队赛了9场,共得17分.已知这个队负了2场,那么这个队胜了几场?平了几场呢?
设勇士队胜了x场,平了y场,可列出方程组:
这就要研究含有两个未知数的方程组了!
★本章将研究一次方程组的解法,并应用一次方程组解决一些实际问题,从中体会消元的思想方法.
什么叫一元一次方程 什么叫一元一次方程的解 怎样检验一个数
是否是这个方程的解
只含有一个未知数、左右两边都是整式,并且含未知数的项的次数都是1的方程叫做一元一次方程.
能使方程左、右两边的值相等的未知数的值,叫做方程的解.
问题1 暑假里,某地组织了“我们的小世界杯”足球邀请赛.比赛规定:胜一场得3分,平一场得1分,负一场得0分.勇士队在第一轮比赛中赛了9场,负了2场,共得17分.那么这个队胜了几场?平了几场呢?
知识点1 二元一次方程(组)的定义
思考 问题1中告诉了我们哪些等量关系?问题1中有两个未知数,如果分别设为x、y,又会怎样呢?
探索 在下列的表格中填入数字或式子.
胜 平 合计
场数 x y 9
得分 17
3x
y
设勇士队胜了x场,平了y场,那么根据题意,得
x+y=9-2 ①
和
3x+y=17. ②
这两个方程
有什么共同
特点?
上面所列方程各含有几个未知数
含有未知数的项的次数是多少
答:2个未知数
答:次数是1
归纳 像这样,有两个未知数,并且含有未知数的项的次数都是1的方程,叫做二元一次方程.
这个问题中,两个未知量(比赛场数)要满足两个等量关系.相应地,两个未知数x、y必须同时满足①②两个方程.因此,把这两个方程合在一起,并写成
归纳 像这样,两个二元一次方程合在一起,就组成了一个二元一次方程组.
注意:方程组各方程中同一字母必须代表同一个量.
例如: x=5 , y=2 是方程x+y=7 的一个解,记作
x=5,
y=2
知识点2 二元一次方程(组)的解
使二元一次方程的左、右两边的值相等的一对未知数的值,叫做二元一次方程的解.
x=5 ,y =2是否为方程 x+y=7的一个解
x=5 , y =2是否为方程 3x +y=17的一个解
x+y=7,
3x+y=17
的解.
{
就是二元一次方程组
x=5
y=2
例如,
{
一般地,使二元一次方程组中两个方程的左、右两边的值都相等的一对未知数的值,叫做二元一次方程组的解.
知识点2 二元一次方程(组)的解
问题3 某校现有校舍20 000m ,计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%.若新建校舍的面积为被拆除的旧校舍面积的4倍,则应拆除多少旧校舍,建造多少新校舍?
知识点3 根据题意列二元一次方程(组)
试一试
若设应拆除x 旧校舍,建造y新校舍,请你根据题意列出方程组.
分析 根据条件可知,题中的等量关系为:
新建校舍的面积=被拆除的旧校舍面积的4倍;
新建校舍的面积-被拆除旧校舍的面积=现有校舍面积的30%.
根据此等量关系列出方程组,
(1)审题:仔细审题,弄清题目中的已知量与未知量及两者之间的联系;
(2)设未知数:弄清题意和题目中的数量关系,设出两个未知数,并用含未知数的代数式表示其他需要的量;
(3)找等量关系:通过阅读理解,找出两个等量关系;
(4)列方程组:根据等量关系,列出二元一次方程组.
根据实际问题列二元一次方程组的步骤:
1. [2024无锡期中] 下列方程组中,是二元一次方程组的是
( )
B
A. B.
C. D.
返回
2. 下列判断中,正确的是( )
D
A. 方程 不是二元一次方程
B. 任何一个二元一次方程都只有一个解
C. 方程有无数组解,任何一组, 的值都是该方
程的解
D. 既是方程的解也是方程 的解
返回
3. 下列各组数值中,是二元一次方程组
的解的是( )
B
A. B.
C. D.
返回
4.[2024沈阳期末] 现用95张纸板制作一批盒子,每张纸板可
做4个盒身或做11个盒底,而一个盒身和两个盒底配成一个
完整的盒子.问用多少张纸板制盒身、多少张纸板制盒底,可
以使盒身和盒底正好配套?设用张纸板做盒身, 张纸板做
盒底,可以使盒身与盒底正好配套,则可列方程是
_ _____________.
5.如果是关于, 的二元一次方程,
则 的值为____.
返回
6. 写出二元一次方程 的一组整数
解:_ _____________________.
7.已知是方程的解,则式子 的
值为___.
(答案不唯一)
1
【点拨】将代入,可得 ,则
.
返回
8. 已知方程组
(1)分别取, ,0,2,填写下表:
方程
0 2
___ ___ ____ ____
方程
0 2
_ _ ___ _ _ ___
8
2
2
4
(2)根据(1)中的数据写出方程组的解.
【解】方程组的解为
返回
二元一次方程组的定义
认识二元一次方程组
二元一次方程组的解
谢谢观看!
