7.1.2不等式的解集 课件(共26张PPT)
文档属性
| 名称 | 7.1.2不等式的解集 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
7.1.2不等式的解集
第7章 一元一次不等式
华东师大版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.理解不等式的解集和解不等式的概念.
2.准确掌握不等式的解集在数轴上的表示方法,能正确地在数轴上表示出不等式的解集.
我会从教学目标、教学重难点、教学方法等方面入手,为你撰写一份完整的教案。
# 一元一次方程教案
## 一、教学目标
1. 知识与技能目标
- 理解一元一次方程的概念,能准确识别一元一次方程。
- 掌握一元一次方程的解法,能熟练求解简单的一元一次方程。
2. 过程与方法目标
- 通过观察、分析、归纳等活动,培养学生的逻辑思维能力和抽象概括能力。
- 经历从实际问题中建立一元一次方程模型的过程,体会方程是解决实际问题的重要数学工具。
3. 情感态度与价值观目标
- 激发学生学习数学的兴趣,培养学生的合作交流意识和勇于探索的精神。
## 二、教学重难点
1. **重点**
- 一元一次方程的概念和方程的解的概念。
- 一元一次方程的解法,特别是移项法则的应用。
2. **难点**
- 从实际问题中抽象出一元一次方程模型,找出等量关系。
- 正确理解和运用移项法则解方程。
## 三、教学方法
讲授法、讨论法、练习法相结合
## 四、教学过程
1. **导入新课(5分钟)**
- 通过展示生活中的实际问题,如购物打折、行程问题等,引导学生思考如何用数学方法解决这些问题,从而引出方程的概念。
2. **讲授新课(25分钟)**
- 一元一次方程的概念
- 展示一些方程,让学生观察它们的特点,引导学生归纳出一元一次方程的定义:只含有一个未知数,并且未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。
- 方程的解的概念
- 给出一些方程,让学生尝试代入不同的值,看哪个值能使方程左右两边相等,从而引出方程的解的概念:使方程左右两边相等的未知数的值叫做方程的解。
- 一元一次方程的解法
- 以简单的一元一次方程为例,如2x + 3 = 7,讲解移项法则:把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项。通过移项将方程化为ax = b(a≠0)的形式,然后求解x = b/a。
3. **课堂练习(15分钟)**
- 给出一些一元一次方程,让学生进行练习,巩固所学的解法。教师巡视指导,及时纠正学生的错误。
4. **课堂小结(5分钟)**
- 与学生一起回顾本节课所学的内容,包括一元一次方程的概念、方程的解的概念以及一元一次方程的解法。
5. **布置作业(5分钟)**
- 布置适量的课后作业,让学生进一步巩固所学知识。
## 五、教学反思
在教学过程中,要注重引导学生积极参与课堂活动,通过实际问题的引入,激发学生的学习兴趣。在讲解一元一次方程的解法时,要注重步骤的规范性和逻辑性,让学生理解每一步的依据。同时,要关注学生的练习情况,及时反馈和纠正学生的错误,确保学生掌握一元一次方程的解法。
这份教案你觉得怎么样?如果你对教学过程中的某个环节还有更具体的要求,比如导入新课的实际问题、课堂练习的题目类型等,都可以告诉我。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
用不等式来刻画比-1大的数为 x >-1.
结合数轴与不等式这两者的相关知识,我们是否可以将不等式的解集在数轴上通过点用含有方向的线段来表示呢
如图所示的数轴,如果在上面标注-1,则比-1大的数位于-1的左边还是右边?
0
-1
知识点1 不等式的解集
不等式x+3<5,除了上面提到的解外,你还能说出它的其他解吗
下列各数中,哪些是不等式x+3<5的解?
l, 0, 2,-2.5, -4, 3.5, 4,4.5,3.
它的解有( ) 个。
无数
知识点1 不等式的解集
不等式的解集:一个不等式的所有解,组成这个不等式的解的集合,简称为这个不等式的解集.
解不等式:求不等式的解集的过程,叫做解不等式.
不等式的解集必须满足两个条件:
1.解集中的任何一个数值都使不等式成立;
2.解集外的任何一个数值都不能使不等式成立.
知识点1 不等式的解集
不等式的解 不等式的解集
区别 范围
示例
联系
能使不等式成立的未知数的值
所有能使不等式成立的未知数的值,通常为取值范围
x=3是2x-3<7的一个解
x<5是2x-3<7的解集
不等式的解与不等式的解集的区别与联系
不等式的解集包含不等式的解,不等式的所有解组成了不等式的解集
知识点1 不等式的解集
例1 判断下列说法是否正确?
(1) x=2是不等式x+3<4的解; ( )
(2) 不等式x+1<2的解有无穷多个; ( )
(3) x=3是不等式3x<9的解 ( )
(4) x=2是不等式3x<7的解集; ( )
√
×
×
×
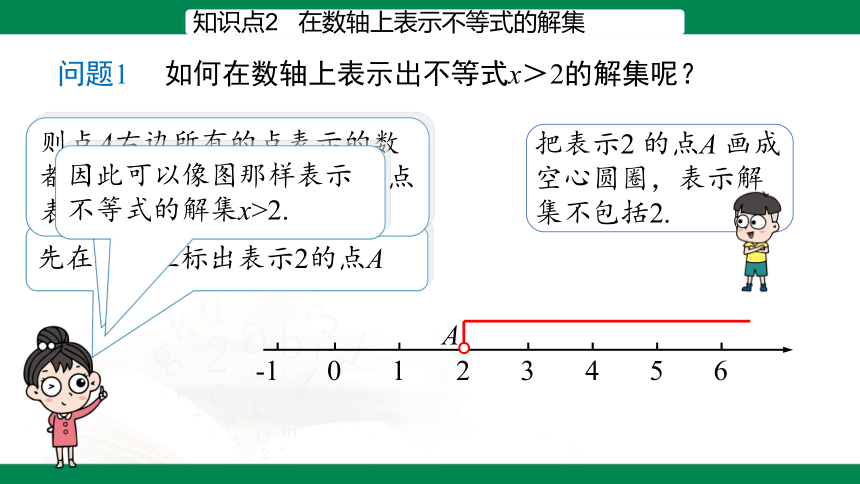
知识点2 在数轴上表示不等式的解集
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2
因此可以像图那样表示不等式的解集x>2.
问题1 如何在数轴上表示出不等式x>2的解集呢?
0
1
2
3
4
5
6
-1
A
把表示2 的点A 画成空心圆圈,表示解集不包括2.
知识点2 在数轴上表示不等式的解集
画一画: 利用数轴来表示下列不等式的解集.
(1) x>-1 (2) x<
0
-1
0
1
用数轴表示不等式的解集,应记住下面的规律:
大于向右画,小于向左画;
>,<画空心圆.
知识点2 在数轴上表示不等式的解集
问题2 在数轴上表示x ≤ 5的解集.
-1
0
1
2
3
4
5
6
解集x≤5中包含5,所以在数轴上将表示5的点画成实心圆点.
符号“≤”表示“小于等于”,“≥”表示“大于等于”.
知识点2 在数轴上表示不等式的解集
用数轴表示不等式解集的方法:
(1)画数轴;
(2)定边界点:若这个点包含于解集之中,则用实心圆点表示;不包含在解集中,则用空心圆圈表示。
(3)定方向:相对于边界点,大于向右画,小于向左画。
1. 下列不等式的解集中,不包括 的是( )
C
A. B. C. D.
2. [2024烟台期中] 下列说法:①是不等式 的一
个解;②不等式的整数解有无数个;③不等式
的解集为 .其中正确的有( )
C
A. 1个 B. 2个 C. 3个 D. 0个
返回
3. 如图,数轴上表示的不等式的解集是
( )
C
A. B. C. D.
向右大于,向左小于,有等号实心点,无等号空心圏.
返回
4. [2024贵州] 不等式 的解集在数轴上表示正确的是
( )
C
A. B.
C. D.
返回
5. “满足 的每一个数都是不等式
的解,所以不等式的解集是 ”,这句
话是否正确?并说明理由.
【解】这句话不正确.因为满足 的数只是不等式
的部分解,如:, 也是不等式
的解,所以 不是其解集,故这句话不正确.
返回
6.在数轴上表示出下列不等式的解集:
(1) ;
【解】如图①所示.
(2) ;
【解】如图②所示.
(3) ;
如图③所示.
(4) .
【解】如图④所示.
返回
7. 有一个数不小于 ,这个数的范围在数轴上表示正确的是
( )
D
A. B. C. D.
返回
8. 如图, 和5分别是天平两边的砝码的质量,
则 的取值范围在数轴上可表示为 ( )
C
A. B.
C. D.
返回
9.已知是关于,的二元一次方程 的一
组解.
(1)求 的值.
【解】由题意得,解得 .
(2)若的取值范围如图所示,试猜想 的最大整数值.
【解】由题意得,即 ,
由数轴知的取值范围为 ,
即,当时, ,
故猜想 的最大整数值为3.
返回
10. 若关于的不等式 有且只有两个负
整数解,求 的取值范围.
【解】 关于的不等式有且只有两个负整数解, 不
等式的负整数解是, .
已知不等式的特殊解确定字母的取值范围时,因为特
殊解有限,所以该字母的范围一定是某一区间,关键是包不包
括端点.为了防止出错,可以把包括和不包括端点分情况讨论.
返回
概念
一个不等式的所有解,组成这个不等式的解的集合
在数轴上表示不等式的解集
小于向左画,大于向右画,无等号空心圆,有等号实心点
不等式的解集
谢谢观看!
7.1.2不等式的解集
第7章 一元一次不等式
华东师大版(2024)数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.理解不等式的解集和解不等式的概念.
2.准确掌握不等式的解集在数轴上的表示方法,能正确地在数轴上表示出不等式的解集.
我会从教学目标、教学重难点、教学方法等方面入手,为你撰写一份完整的教案。
# 一元一次方程教案
## 一、教学目标
1. 知识与技能目标
- 理解一元一次方程的概念,能准确识别一元一次方程。
- 掌握一元一次方程的解法,能熟练求解简单的一元一次方程。
2. 过程与方法目标
- 通过观察、分析、归纳等活动,培养学生的逻辑思维能力和抽象概括能力。
- 经历从实际问题中建立一元一次方程模型的过程,体会方程是解决实际问题的重要数学工具。
3. 情感态度与价值观目标
- 激发学生学习数学的兴趣,培养学生的合作交流意识和勇于探索的精神。
## 二、教学重难点
1. **重点**
- 一元一次方程的概念和方程的解的概念。
- 一元一次方程的解法,特别是移项法则的应用。
2. **难点**
- 从实际问题中抽象出一元一次方程模型,找出等量关系。
- 正确理解和运用移项法则解方程。
## 三、教学方法
讲授法、讨论法、练习法相结合
## 四、教学过程
1. **导入新课(5分钟)**
- 通过展示生活中的实际问题,如购物打折、行程问题等,引导学生思考如何用数学方法解决这些问题,从而引出方程的概念。
2. **讲授新课(25分钟)**
- 一元一次方程的概念
- 展示一些方程,让学生观察它们的特点,引导学生归纳出一元一次方程的定义:只含有一个未知数,并且未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。
- 方程的解的概念
- 给出一些方程,让学生尝试代入不同的值,看哪个值能使方程左右两边相等,从而引出方程的解的概念:使方程左右两边相等的未知数的值叫做方程的解。
- 一元一次方程的解法
- 以简单的一元一次方程为例,如2x + 3 = 7,讲解移项法则:把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项。通过移项将方程化为ax = b(a≠0)的形式,然后求解x = b/a。
3. **课堂练习(15分钟)**
- 给出一些一元一次方程,让学生进行练习,巩固所学的解法。教师巡视指导,及时纠正学生的错误。
4. **课堂小结(5分钟)**
- 与学生一起回顾本节课所学的内容,包括一元一次方程的概念、方程的解的概念以及一元一次方程的解法。
5. **布置作业(5分钟)**
- 布置适量的课后作业,让学生进一步巩固所学知识。
## 五、教学反思
在教学过程中,要注重引导学生积极参与课堂活动,通过实际问题的引入,激发学生的学习兴趣。在讲解一元一次方程的解法时,要注重步骤的规范性和逻辑性,让学生理解每一步的依据。同时,要关注学生的练习情况,及时反馈和纠正学生的错误,确保学生掌握一元一次方程的解法。
这份教案你觉得怎么样?如果你对教学过程中的某个环节还有更具体的要求,比如导入新课的实际问题、课堂练习的题目类型等,都可以告诉我。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
用不等式来刻画比-1大的数为 x >-1.
结合数轴与不等式这两者的相关知识,我们是否可以将不等式的解集在数轴上通过点用含有方向的线段来表示呢
如图所示的数轴,如果在上面标注-1,则比-1大的数位于-1的左边还是右边?
0
-1
知识点1 不等式的解集
不等式x+3<5,除了上面提到的解外,你还能说出它的其他解吗
下列各数中,哪些是不等式x+3<5的解?
l, 0, 2,-2.5, -4, 3.5, 4,4.5,3.
它的解有( ) 个。
无数
知识点1 不等式的解集
不等式的解集:一个不等式的所有解,组成这个不等式的解的集合,简称为这个不等式的解集.
解不等式:求不等式的解集的过程,叫做解不等式.
不等式的解集必须满足两个条件:
1.解集中的任何一个数值都使不等式成立;
2.解集外的任何一个数值都不能使不等式成立.
知识点1 不等式的解集
不等式的解 不等式的解集
区别 范围
示例
联系
能使不等式成立的未知数的值
所有能使不等式成立的未知数的值,通常为取值范围
x=3是2x-3<7的一个解
x<5是2x-3<7的解集
不等式的解与不等式的解集的区别与联系
不等式的解集包含不等式的解,不等式的所有解组成了不等式的解集
知识点1 不等式的解集
例1 判断下列说法是否正确?
(1) x=2是不等式x+3<4的解; ( )
(2) 不等式x+1<2的解有无穷多个; ( )
(3) x=3是不等式3x<9的解 ( )
(4) x=2是不等式3x<7的解集; ( )
√
×
×
×
知识点2 在数轴上表示不等式的解集
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2
因此可以像图那样表示不等式的解集x>2.
问题1 如何在数轴上表示出不等式x>2的解集呢?
0
1
2
3
4
5
6
-1
A
把表示2 的点A 画成空心圆圈,表示解集不包括2.
知识点2 在数轴上表示不等式的解集
画一画: 利用数轴来表示下列不等式的解集.
(1) x>-1 (2) x<
0
-1
0
1
用数轴表示不等式的解集,应记住下面的规律:
大于向右画,小于向左画;
>,<画空心圆.
知识点2 在数轴上表示不等式的解集
问题2 在数轴上表示x ≤ 5的解集.
-1
0
1
2
3
4
5
6
解集x≤5中包含5,所以在数轴上将表示5的点画成实心圆点.
符号“≤”表示“小于等于”,“≥”表示“大于等于”.
知识点2 在数轴上表示不等式的解集
用数轴表示不等式解集的方法:
(1)画数轴;
(2)定边界点:若这个点包含于解集之中,则用实心圆点表示;不包含在解集中,则用空心圆圈表示。
(3)定方向:相对于边界点,大于向右画,小于向左画。
1. 下列不等式的解集中,不包括 的是( )
C
A. B. C. D.
2. [2024烟台期中] 下列说法:①是不等式 的一
个解;②不等式的整数解有无数个;③不等式
的解集为 .其中正确的有( )
C
A. 1个 B. 2个 C. 3个 D. 0个
返回
3. 如图,数轴上表示的不等式的解集是
( )
C
A. B. C. D.
向右大于,向左小于,有等号实心点,无等号空心圏.
返回
4. [2024贵州] 不等式 的解集在数轴上表示正确的是
( )
C
A. B.
C. D.
返回
5. “满足 的每一个数都是不等式
的解,所以不等式的解集是 ”,这句
话是否正确?并说明理由.
【解】这句话不正确.因为满足 的数只是不等式
的部分解,如:, 也是不等式
的解,所以 不是其解集,故这句话不正确.
返回
6.在数轴上表示出下列不等式的解集:
(1) ;
【解】如图①所示.
(2) ;
【解】如图②所示.
(3) ;
如图③所示.
(4) .
【解】如图④所示.
返回
7. 有一个数不小于 ,这个数的范围在数轴上表示正确的是
( )
D
A. B. C. D.
返回
8. 如图, 和5分别是天平两边的砝码的质量,
则 的取值范围在数轴上可表示为 ( )
C
A. B.
C. D.
返回
9.已知是关于,的二元一次方程 的一
组解.
(1)求 的值.
【解】由题意得,解得 .
(2)若的取值范围如图所示,试猜想 的最大整数值.
【解】由题意得,即 ,
由数轴知的取值范围为 ,
即,当时, ,
故猜想 的最大整数值为3.
返回
10. 若关于的不等式 有且只有两个负
整数解,求 的取值范围.
【解】 关于的不等式有且只有两个负整数解, 不
等式的负整数解是, .
已知不等式的特殊解确定字母的取值范围时,因为特
殊解有限,所以该字母的范围一定是某一区间,关键是包不包
括端点.为了防止出错,可以把包括和不包括端点分情况讨论.
返回
概念
一个不等式的所有解,组成这个不等式的解的集合
在数轴上表示不等式的解集
小于向左画,大于向右画,无等号空心圆,有等号实心点
不等式的解集
谢谢观看!
